近饱和状态下干线协调子区划分方法研究
2021-11-04天津职业技术师范大学汽车与交通学院王新建
天津职业技术师范大学汽车与交通学院 / 王新建
一、近饱和状态下交叉口关联度模型适应性分析
通过前文国内外研究现状可得,目前子区划分方法研究大多基于交叉口关联度,来判定交叉口划入子区的必要性。因此,交叉口关联度模型适应性是子区划分的基础步骤。
对于子区划分而言,每一种关联度模型都存在其适用范围,并不能适用于所有的交叉口状况。尤其是近饱和状态道路进行子区划分时,交通状况较为复杂,必须对交叉口关联度模型的内涵及适应性进行对比分析,并结合路段、交叉口自身特性,挑选或者改进出能够应用于工程实践的交叉口关联度模型。本文选取以下两类最常用的模型展开适应性分析。
(一)相聚度模型
近些年来学者将相聚度模型应用于子区划分,将子区划分问题转化为多目标群体决策问题。交叉口群体偏好矢量能够拥有数个评价目标,因此可以选取合适的参数作为评价目标。具体计算公式如公式(2.3)所示:

(二)协调效益模型
交叉口划入同一子区的必要程度,由模型中的协调因子(CF)来度量,CF值的大小与交叉口合并的必要性成正比。CF具体公式如公式(2.4)所示:

(三) Whitson及其改进模型
Whitson模型,所需基础参数少且容易获取、计算简便,是应用最为广泛的模型。具体计算公式如公式(1.3)所示:

式中:I——上右游交叉口关联性指数;
n——上游车流驶入下游的路径数量;
t——通过上下游交叉口停车线的平均行程时间;
qmax——上游交叉口最大的路径流量。
交叉口划入同一子区的需求程度与I值成正比,该模型行程时间中没有考虑排队车辆导致的行程时间变化。国内学者高云峰对此进行了改进,将行程时间变为从上游交叉口停车线行驶至下游交叉口排队末尾的行程时间,具体计算如公式(1.4)所示:

qmax——上游交叉口最大的路径流量,veh/h;
t——从上游交叉口停车线行驶至下游交叉口排队末尾的行程时间,s。
Whitson及其改进模型均以相关因素的比值为度量指标,没有深入探究影响子区划分的内在机理,无法适用于日益趋向于精细化管理的城市道路。
(四)算法适应性分析
根据国内外的研究,一般采用的一些分区方法都是基于相交关系。在节中,针对分区划分,分区方法的每一部分都有应用领域。优化了不同条件下的变化效果。特别是在接近饱和的条件下,由于道路状况复杂,有必要对一些区域划分体系的特点和适应性进行比较分析,选择或修改一些可以提高运输效率的算法。选择了以下两种最常见的算法进行自适应分析。
1.遍历搜索法
考虑到主信道上的所有交叉点,循环搜索在指定的搜索序列中被序列分割。这个方法简单,容易实现。可以选择最合适的。但是,接近饱和时,所有的交叉点都饱和。因此,一般的布线方法适用于流量少、峰值低的道路。
其次,由于遍历搜索算法的特殊性,所以当交叉数过多时,计算时间增加了几倍,因此该方法也可以应用于不太崎岖的路径。
2.聚类分析法
当道路接近饱和时,交叉路口的车辆会导致交通效率下降,队列不断堆积。一些车辆到达后,由于拥挤的十字路口交通效率低下,仍然向上游延伸,车辆不太可能到达下路口;而在消息的下端交叉口,消息相对稳定。
分组分析方法可以快速筛选功能节点,找到溢出的交叉点;但是,如果所有交叉点都平滑溢出,因此,这种方法不适合在交通密度低、交通高峰期修建道路。由于算法本身的局限性,它很容易局部优化,每次都不可能得到最优方案。
本文选取遍历搜索算法进行改进,由于本文选取基于交叉口关联度的子区划分方法展开研究,因此不会将所有交叉口当作同一级别,有利于子区划分。
而在城市干线道路进行子区划分,如果直接进行遍历择优选取最优方案,随着交叉口数的增加,子区划分难度也逐步增加。因此,选取二次划分的方法,先进行子区初步划分,再进行子区的细划分,可以使运算结果快速收敛,减少运算时间,弥补遍历搜索的缺陷。
二、基于近饱和状态的交叉口关联度模型构建
现有交叉口关联度模型,仅仅考虑交叉口之间关联性,忽略了实际协调控制效果,导致子区划分、信号协调控制之间并无有效衔接,无法保证交通效益为最优。因此本文基于子区协调效果,考虑绿波、红波协调两种控制方式,分别构建其对应的关联度模型。
(一)基于绿波的交叉口关联度模型
绿波协调的目的是使车辆能够不停车连续通过数个交叉口,为能够达成周期性规律,需要实施公共周期、调整相位差来实现。绿波带是指协调相位绿灯时间内平行的上下两条速度斜线、左右两边的绿灯时间构成的平行四边形。在工程实践中需要不断调整相位差、绿波速度形成绿波带。
绿波带宽,指的是绿波带左右两边的时间高度,表征协调相位的交通流在理想状态下,能够保持一定速度不停车连续通过数个交叉口的绿灯放行时间,是评价绿波协调效果的关键性指标。关于每一个子区的绿波带宽大小并没有一个规定的阈值,并不是越大越好、越小越差,需要依据实际状况评价其是否与流量匹配,是否充分利用了时空资源。
为了使关联性大的交叉口能够合并为一个子区,引用乐浩成提出的绿波带宽到达率的概念,来表征子区划分方案下绿灯时间的利用率,如公式(3.1)所示。
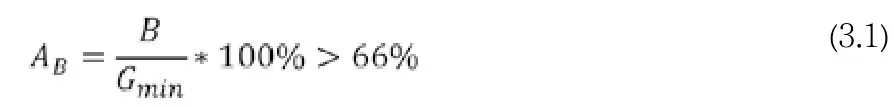
式中:AB——绿波带宽到达率(%);
B——最大绿波带宽(s);
Gmin——协调相位最小绿灯时间(s)。
模型中采用的为理想状态,车辆全部为匀速行驶的直行车辆,并没有考虑交通流离散性。实际工程实践中的绿波带宽会变小。因此往往以实际绿波带宽到达率作为子区划分目标,以保证绿波协调的实际通行效果,如公式(3.2)所示。

式中:Bre——实际绿波带宽(s);
ABre——实际绿波带宽到达率(%)。
引用黄鸿科在《干线协调控制效果可靠性研究》中提出的:当实际绿波带宽与设计绿波带宽的差值在设计绿波带宽的25%时,能够满足实际需求,协调效果是可靠的。计算可得当道路上下行的数值均大于等于49.5%时,说明划分效果优良。
计算所有绿波子区实际绿波带宽到达率的算数平均值,作为子区划分系统对于绿灯时间利用率的度量。当数值越高,说明子区划分的效果越好;反之则划分效果越差。并且道路上行、下行数值其中一者不满足条件,则划分效果不佳。具体目标函数如公式(3.3)所示。

式中:AB(t)——干线双向综合实际绿波带宽(s);
AB(d)——为下行实际绿波带宽(s);
AB(u) ——上行绿波带宽(s);
β1、β2——权重系数;
qd——下行方向流量(veh/h);
qu——上行方向流量(veh/h)。
子区的实际绿波带宽数据无法直接获取。
(二)基于红波的交叉口关联度模型
红波控制能够均匀分配协调相位对应的流量,缓解下游交叉口拥堵。但在流量较小的情况下,实施红波控制会增加交叉口延误,降低驾驶体验。因此只有当道路近饱和状态下,实施绿波控制无法缓解道路压力时,需要进行红波控制。
红波协调控制是指实施公共周期、调整相位差后,行成周期性规律,使车辆在上游绿灯启亮后,行驶至下游交叉口遇见红灯,等到绿灯启亮后,行驶至下一个交叉口依旧遇见红灯,直至行驶至瓶颈交叉口。红波协调控制在判断瓶颈交叉口后,以上游交叉口停车线、交叉口之间路段为缓冲空间,将原本行驶至瓶颈交叉口的车辆进行截留,整个红波子区内的交叉口形成一个截流控制系统,使交通流均匀分布于各个交叉口,缓解溢流状况。红波协调控制的目的是缓解道路溢流状况,其中溢流状况是否有改善,是评价红波协调控制效果的关键性指标。
交通溢流是指交叉口排队车辆长度大于路段长度,会导致车辆延误增大,甚至出现交叉口锁死现象。因此,判断道路溢流是预防道路瘫痪的重要判别指标。若交叉口协调相位的交通需求过大,而供给的绿灯时间较短,会导致每个信号周期都会有车辆滞留。因此以直行溢流状态作为交叉口关联度,构建直行溢流状态判定模型。如公式(3.4)所示。

式中:Sk(of)——子区K的溢流状态,若为1则发生溢流,反之则不发生;
tn——协调相位车辆完全通过下游交叉口所需时间(s);
tp——下游交叉口可供上游车辆不停车通过的绿灯时间(s)。
三、基于交叉口关联度的子区划分模型构建
在近饱和状态下,可以有效地提高信号控制的优化效果,在干线协调信号控制过程中,复杂和大规模的信号控制问题可以通过道路划分来转换成几个简单和小的信号控制问题。该方法是可以大幅提高道路效率和服务水平的部分区域划分。本文提出防溢流为优化目标的红波子区划分模型。道路进行红波控制时,把上游交叉口In划入子区,实施公共周期、调整相位差后,如果道路溢流状态没有缓解,说明交叉口In需要划入子区,并且需要将上游交叉口继续划入该子区对交通流截流处理;如果道路溢流状态缓解,说明将交叉口In划入子区后已经能够缓解道路压力,子区划分结束。
(一)绿波子区划分模型构建
当交通信号工程师使用最大绿波带宽模型时,考虑的关键因素是绿波带宽。该因素能够显示子区划分方案的优劣。其次为了保证双向绿波效果,将会牺牲一定的绿波带宽保证较少的停车次数,因此绿波带宽的大小能够一定程度表明绿波协调的效果与稳定性。
本文根据实际设定具体的合并、分离阈值,并以子区划分方案带宽为最优目标,考察各个方案的优劣。
在绿波子区划分时,首先需要考虑设计的协调方案是否能够满足现有的交通流需求,引用黄鸿科在《干线协调控制效果可靠性研究》中提出的:当实际绿波带宽与设计绿波带宽的差值在设计绿波带宽的25%时,能够满足实际需求。
约束条件主要有以下几点:
1.当交叉口划入子区,子区的实际绿波带宽差值大于阈值时,子区不可以接受交叉口;反之则接受。
2.当交叉口划入子区,子区的实际绿波带宽到达率小于阈值时,子区不接受交叉口;反之则接受。

式中:PI——最大期望的协调效益;
Skg——再次划分绿波子区,其他意义同上。
(二)红波子区划分模型构建
在子区初步划分的基础上,本文提出防溢流为优化目标的红波子区划分模型。道路进行红波控制时,把上游交叉口In划入子区,实施公共周期、调整相位差后,如果道路溢流状态没有缓解,说明交叉口In需要划入子区,并且需要继续将上游交叉口继续划入该子区对交通流截留;如果道路溢流状态缓解,说明将交叉口In划入子区后已经能够缓解道路压力,子区划分结束。具体划分模型如公式(4.2)所示。

式中:Skr——再次划分红波子区;
Skr(In)——交叉口In是否划入红波子区,若为1则划入,反之则不划入;
Sk(of)——子区K的溢流状态,若为1则发生溢流,反之则不发生,其他意义同上。
该模型能够结合交通效益,量化交叉口关联度,实施子区的精细化管理。
子区划分方法作为交通管理的重要工作。科学合理的分区计划不仅缓解了交通拥堵,还增加了道路资源的时空利用性,为开车创造了有利条件。科学合理的子区划分方案,不仅能够缓解道路拥堵状况、提高道路资源的时空利用率,也能给驾驶员提供一个良好的驾驶体验环境。本文对当今国内外干线协调子区划分方法研究成果进行研究,分析总结了关联度模型和子区划分算法两方面的研究成果与方向,构建了近饱和状态的交叉口关联度模型,并以近饱和状态为研究背景,综合考虑红波、绿波协调的交通效益,分别构建了能够充分挖掘道路时空资源的红波、绿波交叉口关联度模型,给出了详细的推算过程,打造了一套科学有效子区划分方法,而且还从交叉口关联度入手,并结合工程实践经验,综合考虑了现有方法的不足之处,进行子区的二次划分,使子区划分更加高效便捷。
