基于碰撞波形与约束系统耦合的汽车安全性改进

唐洪斌，刘乐丹，张君媛

（1.中国第一汽车股份有限公司研发总院，长春130013；2.吉林大学汽车工程学院，长春130022；3.汽车振动噪声与安全控制综合技术国家重点实验室，长春130013）

前言

汽车安全性由车体结构和乘员约束系统两方面共同决定。目前整车安全性开发流程主要是在整车结构的抗撞性设计后再进行约束系统匹配。约束系统设计处于一个较为被动的地位，很难达到弥补车体结构设计缺陷的效果。如果在安全性设计初期从耦合关系角度出发，提出车体结构的抗撞性和乘员约束系统设计要求，就可以对匹配效果进行整体把控。

在乘员碰撞力学研究中，Huang［1］提出经典的单自由度模型，合理地阐述碰撞过程中车辆、乘员、约束系统三者间的相互关系，利用单自由度模型可对乘员加速度响应快速求解，为耦合关系研究提供了基础。Cheng等［2］提出了车体与约束系统最佳匹配设计是使乘员响应为一个恒定值，即通过耦合作用使碰撞加速度与乘员相对加速度可互相抵消。Qiu等［3］在碰撞波形简化为矩形波的前提下，提出设计初期平均分配ridedown能量与约束能量，从而提高约束系统与车体结构的耦合效果。上述研究初步提出了碰撞波形与约束系统耦合关系的设计思想，但还没有形成可用于汽车被动安全开发过程的具体设计方法和量化的评价准则。

在上述研究的基础上，吉林大学张君媛［4］提出碰撞波形与约束系统耦合关系评价方法，建立量化的评价准则，并将评价准则与碰撞星级联系起来，从而指导碰撞波形和约束系统的设计。该方法选择工程上广泛应用的等效双梯形波和三线性约束刚度分别作为碰撞加速度波形和约束系统刚度简化方式，并结合60款车US⁃NCAP正面全宽刚性壁障碰撞试验数据，确定等效双梯形波和三线性约束刚度参数范围。利用单自由度模型迭代算法实现乘员加速度响应的求解，确定了乘员响应与碰撞波形参数及约束系统刚度参数变化规律与灵敏度。并在此基础上，采用回归分析方法提出两个刚度值及其耦合关系的评价指标，最终与碰撞星级联系起来。该评价方法一方面有助于现有车型的星级评估，另一方面也可以作为新车的目标设计依据或对已有车型提供改进方向。

本文中利用耦合关系评价方法，对某乘用车型的碰撞波形、约束系统特性和两者之间耦合关系进行评价，提出该车型碰撞波形和约束系统参数优化方案，指导该车型车体结构和乘员约束系统改进设计，最终有效提高了整车安全性。

1 汽车碰撞波形与约束系统特性耦合关系评价方法

1.1 基于单自由度模型的乘员响应面建立

单自由度模型如图1所示。将车辆与乘员分别简化为集中质量块M和m，车体结构在碰撞中的压溃过程简化为弹簧刚度K的压缩过程，约束系统在碰撞中的变形过程简化为弹簧刚度k的压缩过程，因此乘员的响应由两个弹簧振动系统的耦合关系决定。乘员在汽车碰撞波形P的减速环境下与约束系统作用，因此单自由度模型通常等效为如图2所示的形式［5］。

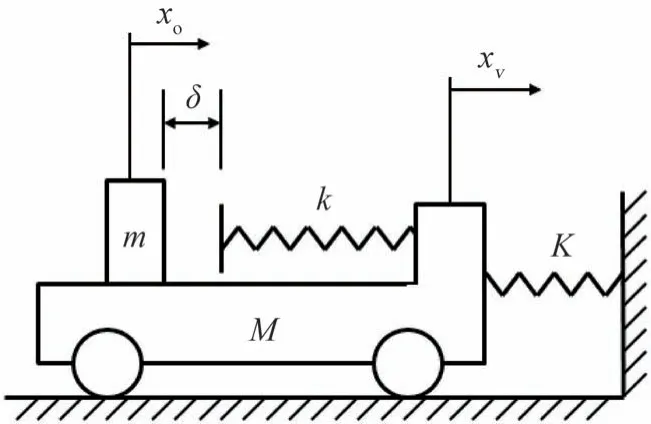
图1 单自由度模型

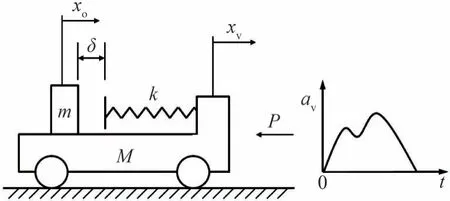
图2 等效单自由度模型

在确定较为准确的K和k简化方式基础上，利用单自由度模型迭代算法可实现乘员加速度响应快速准确的求解。如图3所示，选择应用较为广泛的等效双台阶波作为碰撞波形简化方式，即单自由度模型中K近似为等效双梯形波；选择三线性约束刚度作为约束系统刚度简化方式，即单自由度模型当中k近似为三线性约束刚度。

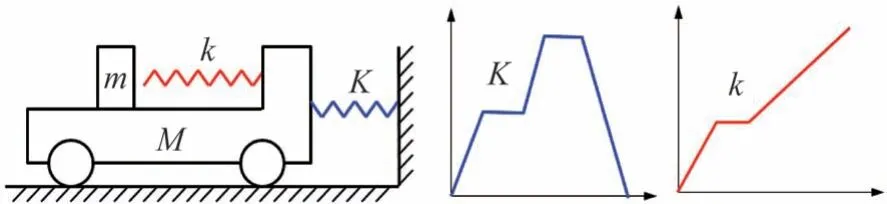
图3 单自由度模型求解

随后，为在一个较大范围内考察波形参数和约束系统参数对乘员响应的影响，从NHTSA统计了包括不同星级的60辆车US⁃NCAP正面全宽刚性壁障碰撞试验数据，提取每辆车的原始碰撞加速度波形和约束系统刚度曲线，用单自由度模型迭代算法快速进行乘员响应求解，最终得到乘员加速度峰值响应面。如图4（a）所示，x轴代表碰撞波形，y轴代表约束刚度，z轴为乘员加速度峰值。将数据库中每个碰撞波形所对应的所有乘员加速度峰值求平均值，记为“波形平均响应Av”；将数据库中每个约束系统对应的所有乘员加速度峰值求平均值，记为“约束平均响应Ar”。为更清楚地表达响应面的规律，将x、y轴从小到大排序，得到排序后的响应面如图4（b）所示。沿着x坐标方向代表随着Av的增大整个响应面都呈现出递增趋势，显示了碰撞波形输入时乘员加速度响应峰值平均水平的变化；同样沿着y坐标方向随着Ar的增大整个响应面呈现出递增趋势，显示了约束系统刚度作用下乘员加速度响应峰值平均水平的变化。由此Av可以近似作为碰撞波形的评价依据，Ar可以作为评价约束系统刚度的依据。

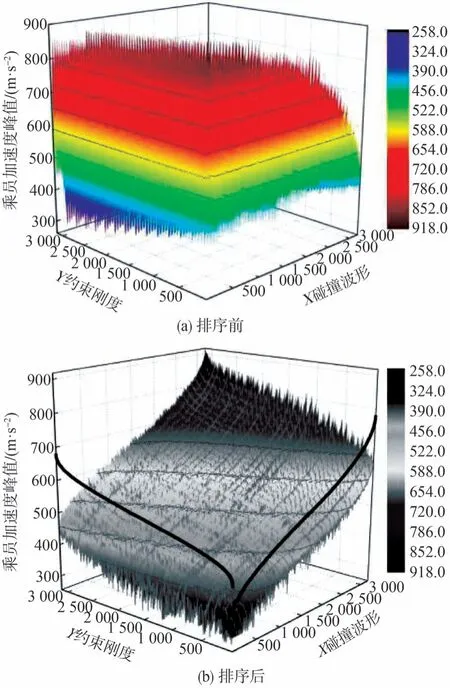
图4 乘员加速度峰值响应面

1.2 碰撞波形、约束系统特性及其耦合关系评价

通过灵敏度分析并结合双台阶波形特点，如图5所示，选择等效双梯形波的G0（形心加速度）、G1（第1台阶高度）、G2（第2台阶高度）、tE（车辆回弹时刻，即双梯形波第2台阶的结束时刻）、tc（发动机碰撞时刻，即双梯形波第1台阶的结束时刻）、KAE（车体前端结构的平均刚度，即双梯形波第2台阶高度与最大压溃量之比）为耦合评价参数。同理，如图6所示，选择三线性刚度曲线的k1（第1段的斜率）、K2（第3段的斜率）、GL（中间段平台的高度）为耦合评价参数。

图5 等效双台阶波

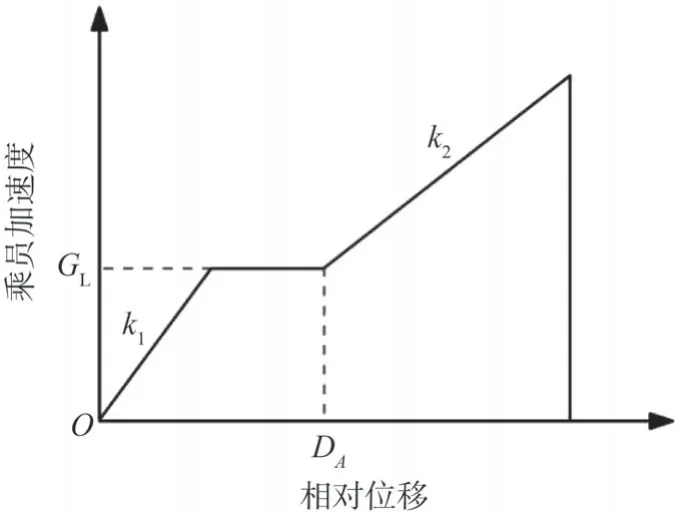
图6 三线性刚度曲线

根据1.1节中的分析，分别将Av和Ar写成下列函数形式：

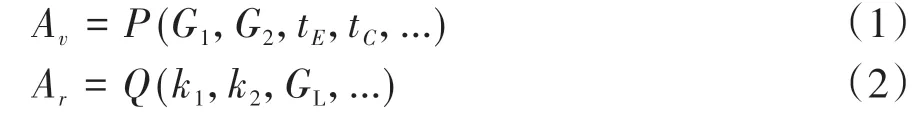
任意一组P和Q的参数组合在乘员响应面上都对应唯一的乘员加速度响应a0。

假设乘员响应a0与Av和Ar之间存在一种函数关系：

若能确定以上函数关系便可建立波形参数与约束系统特性耦合关系的评价方法。

该评价方法的建立过程如下：

（1）确定函数P，根据碰撞波形参数实现碰撞波形的单独评价；

（2）确定函数Q，根据约束系统刚度参数实现约束系统特性的单独评价；

（3）确定函数R，根据碰撞波形和约束系统特性的单独评价结果进行整体耦合关系评价。

通过构建多元二次回归模型，得到函数P，并采用min⁃max标准化方法，对Av作标准化处理，得到无量纲的碰撞波形评价指标，定义为“碰撞波形综合评价指标”，用符号γ表示，γ分布在0~1之间，仅从乘员加速度角度考虑，该值越小对应的碰撞波形越好。γ计算公式为

同理，得到无量纲的约束系统特性的评价指标，定义为“约束系统综合评价指标”，用符号β表示，分布在0~1之间，仅从乘员加速度角度考虑，该值越小对应的约束系统刚度越好。计算公式为

通过碰撞波形综合评价指标γ和约束系统综合评价指标β，可以分别对碰撞波形和约束系统特性作出初步的单独评价。然而乘员最终的保护效果是由碰撞波形和约束系统特性两者共同决定的。因此采用曲面拟合的方法近似构造a0与γ和β之间的递增函数关系R，曲面拟合公式为

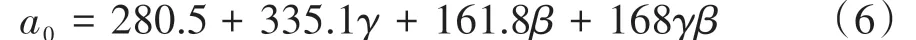
在碰撞波形和约束系统特性的初步单独评价的基础上，通过对γ-β-a0乘员响应面的拟合，建立了γ和β与乘员加速度响应之间的量化关系，实现碰撞波形与约束系统特性的耦合关系评价。

将上述耦合关系评价与NHTSA的星级结果作关联性对比，以考察耦合关系的有效性。通过统计1.1节中的60款车数据，发现乘员胸部加速度与星级之间有很强的相关性，可认为392 m/s2为四星级评价和五星级评价的分界线，490 m/s2为三星级评价和四星级评价的分界线。将γ-β-a0响应面按照392和490 m/s2分界制作等高线图，如图7所示，并将该图称为“星级预估图”。图7将各种耦合情况划分成三星级及以下区域、四星级区域和五星级区域。根据碰撞波形综合评价指标γ与约束系统综合评价指标β的取值可以实现星级预估。将（γ，β）平面坐标位置定义为耦合点，当耦合点处于某区域时，说明取得对应星级的可能性较大。

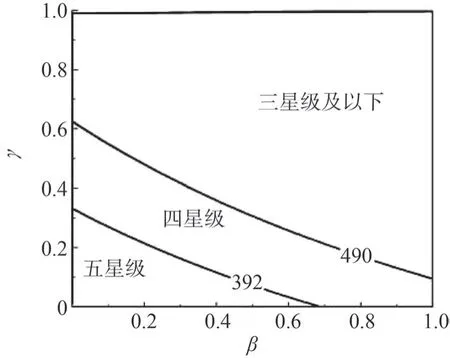
图7 星级预估图

为方便描述，将γ、β的区间0～0.2、0.2～0.4、0.4～0.6、0.6～0.8、0.8～1定义为优、良、中、差、极差的情况。当W5车型碰撞波形对应γ处于优区间时，约束系统对应β处于中区间之前都有可能得到五星级评价，甚至β处于极差区间也很有可能获得四星级评价。当γ处于差区间或极差区间时，无论β如何取值获得三星级及以下评价的可能性都很大。

2 W5车型初始性能分析与耦合关系评价

2.1 W5车型原始性能分析

选用W5车型为研究对象，整车总长为4 535 mm，总宽为1 775 mm，总高为1 427 mm，轴距为2 671 mm，整车整备质量为1 365 kg。W5车型有限元模型如图8所示，包括节点452 882个，单元447 660个，其中三角形单元24 311个，占总数的5.4%，四边形单元409 597个，六面体单元16个，弹簧阻尼单元12个，质量单元889个，铰链单元89个，焊点单元7 808个，梁单元169个，六角八面体退化的六面体单元4 769个。应用LS⁃DYNA软件进行正面100%刚性壁障碰撞仿真，其碰撞波形如图9所示。

图8 W5车型有限元模型

图9 W5车型的碰撞波形

同时，建立W5车型的US⁃NCAP正面100%刚性壁障碰撞试验驾驶员侧约束系统的MADYMO模型，如图10所示。该模型包括安全带、安全气囊、座椅、转向管柱等约束系统装置，放置了Hybrid III第50百分位多刚体假人，以汽车碰撞波形作为该模型加速度场，模拟整车的减速环境。该模型的主要约束系统特性参数见表1，仿真计算的驾驶员胸部加速度-相对位移曲线作为约束系统特性曲线，如图11所示。

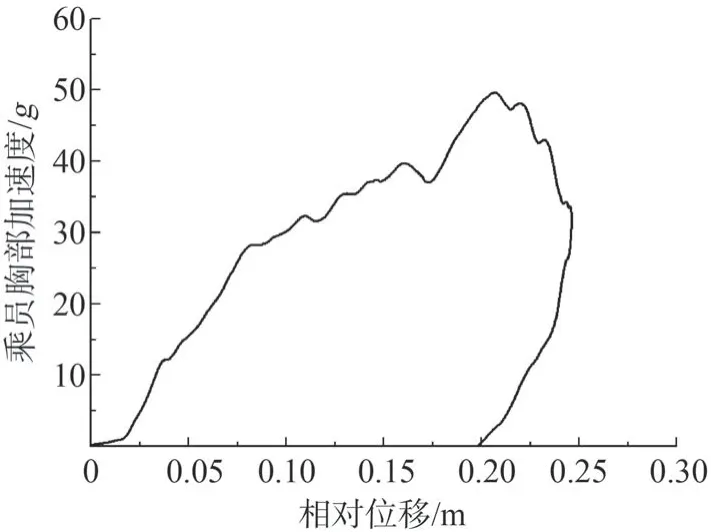
图11 W5车型的约束系统特性曲线

表1 W5模型的约束系统主要特性参数

图10 W5驾驶员约束系统仿真模型

根据US⁃NCAP星级计算方法［6］，将仿真得到的假人各部位伤害指标转换成相应的伤害风险概率，得到乘员伤害相对风险得分（RRS），具体结果如表2所示，W5车型获得了三星级评价。

表2 正面碰撞驾驶员假人评定结果

2.2 W5车型碰撞波形与约束系统特性耦合关系评价

根据2.1节的仿真结果，可知W5车型初始双台阶和约束系统刚度参数，如表3所示。

表3 W5车型双台阶波与约束系统刚度参数

根据表中参数可以实现W5车型耦合关系评价：

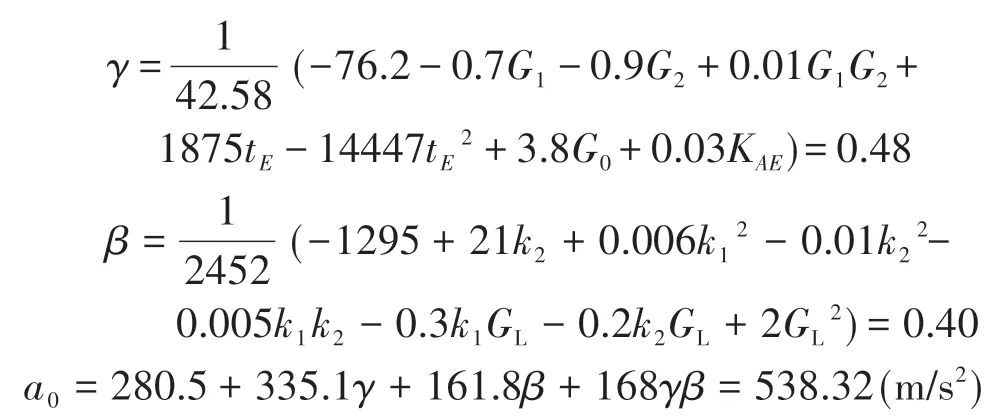
计算得到W5车型的碰撞波形综合评价指标γ为0.48，约束系统综合评价指标β为0.40，相对而言碰撞波形更差一些。将W5车型的耦合点绘制在星级预估图上，如图12所示。耦合点处于三星级区域。由于γ和β都处于中区间，因此W5车型的碰撞波形和约束系统都存在一定的提升空间。

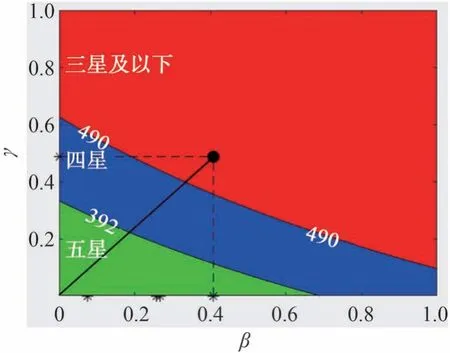
图12 W5模型耦合点在星级预估图位置

3 基于耦合评价的W5车型改进设计

3.1 碰撞波形与约束系统参数匹配优化

首先讨论在不修改W5车型的车体结构基础上进行约束系统参数的匹配优化。

γ=0.48，根据式（6）确定β范围如下：

可认为只有当β处于优区间时才有可能达到四星级。仅从乘员加速度层面考虑，理论上取β为0对应的约束系统参数应该是约束系统最佳匹配情况，a0的值为

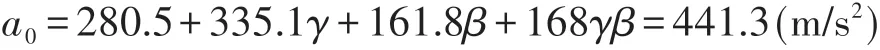
在不改变W5车型碰撞波形的情况下，对约束系统匹配优化方案为：采用β为0时对应的约束系统参数（k1、k2、GL分别取460g/m、160g/m、30g）。最终乘员加速度峰值可达到441.3 m/s2，星级评价预估为四星。也就是说，仅仅通过调整约束系统参数基本只能提高到四星级，在保持现有车体结构对应γ不变的情况下，无论β如何取值，W5车型达到五星级的可能性都很小，只有通过进一步改进碰撞波形才有较大可能达到五星级。

如果保持现有约束系统不变，β=0.4，根据式（6）确定γ范围如下：

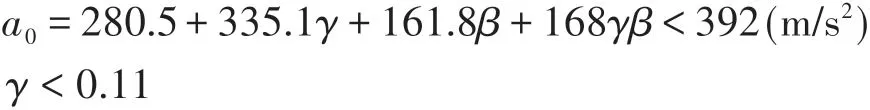
得到对应的γ区间为0～0.16。当γ为0时，a0的值为

同时对W5车型的车体结构和约束系统参数匹配进行优化。在星级预估图将W5车型的耦合点与坐标原点相连（见图13），为确保优化后的车辆100%正面全宽碰撞品质有更高的概率得到五星级，取该连线在五星级区域内中心点附近一点作为目标耦合点。将目标耦合点分解为目标碰撞波形和目标约束系统，读取其横纵坐标可以分别得到目标碰撞波形综合评价指标γ为0.16，目标约束系统综合评价指标β为0.13，代入式（6）中可得a0的值为

图13 W5模型目标耦合点在星级预估图位置

3.2 车体结构与约束系统参数匹配工程方案

在3.1节中应用耦合评价方法从单独优化约束系统参数、单独优化碰撞波形参数、碰撞波形与约束系统参数匹配优化3个角度出发，得到3种优化方案。但在工程中还要将理论参数落实到相关的车体结构和约束系统上，这就要考虑工艺和成本等因素进行相关结构或配置的优化。

3.2.1 碰撞波形与约束系统参数工程方案设计

在实际工程应用中，要实现车辆的星级评价预估为五星，通过单独优化约束系统参数和单独优化碰撞波形参数难度较大，并面临更高的成本代价。从车辆设计生产的经济性出发，在工程应用一般采取同时对车体结构和约束系统参数匹配进行优化的设计方案，实现星级评价预估为五星的设计目标。

根据3.1节中碰撞波形与约束系统参数匹配优化方案分别得到了目标碰撞波形综合评价指标γ为0.16，目标约束系统综合评价指标β为0.13。从NHTSA统计的不同星级的60辆车型US⁃NCAP正面全宽刚性壁障碰撞试验数据中分别选取对应碰撞波形综合评价指标γ为0.16和约束系统综合评价指标β为0.13的两组数据作为目标双台阶波和目标约束系统刚度。分别对车辆原始双台阶波和原始约束系统刚度进行优化。

从数据中找到的碰撞波形综合评价指标γ为0.16的目标波形［7］，表4为目标波形的耦合评价参数。将原始双台阶波与目标双台阶波进行比较，如图14所示。可以得到需要将原始双台阶波第1台阶提高，将第2台阶降低，且延后原始波形的结束时间。

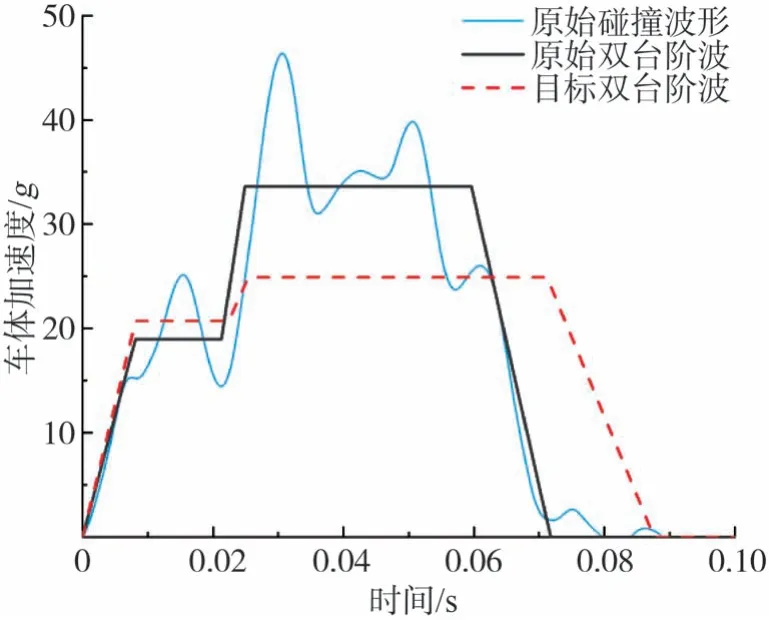
图14 原始简化双台阶波与目标双台阶波对比

表4 碰撞波形评价参数

3.2.2 车体结构改进设计

车辆正面碰撞过程中，主要由防撞梁、吸能盒、前纵梁、shotgun和副车架等车辆前端结构（图15）压溃变形吸收车辆的动能，其中由防撞梁、吸能盒和前纵梁吸收的能量约占车辆前端结构吸能的50%［8］。因此，将通过改变原车上这3处前端结构以实现将原始的碰撞双台阶波改进为目标双台阶波的目的。

图15 车辆前端主要部分吸能结构

通过将碰撞仿真结果和碰撞波形进行对照，如图16所示，可以确定碰撞波形每一段区域对照的车体前端吸能结构。例如当车辆碰撞压缩达到接触发动机的时刻时，车体前端吸能结构的形变主要发生在发动机前端的防撞梁、吸能盒和前纵梁前段。对照简化双台阶波可知，第1台阶的峰值和宽度与防撞梁、吸能盒和前纵梁前段3个结构的吸能性能相关。由此可通过改进对应部分的车体结构，实现对于碰撞波形的优化。而在发动机碰撞时刻之后，及简化双台阶波的第2台阶，则主要受前纵梁中段和后段两个结构吸能性能的影响，可以通过改进这两个车体结构以实现对双台阶波第2台阶的调整。

图16 碰撞波形与车体结构压溃位置对应

要将原始碰撞波形的简化双台阶波的第1台阶改进为目标双台阶波的第1台阶，须提升原始波形第1台阶的高度，即须提升第1台阶波所对应的防撞梁、吸能盒和前纵梁前段3个主要车体吸能结构的吸能效果。在不改变车体结构形状的前提下，可以通过增加3个车体结构的厚度使结构具有更好的吸能效果［9-10］。同时从车体结构轻量化的角度考虑，通过改变这3个车体结构中吸能量较多的前纵梁前段的截面形状，将前纵梁前段的矩形截面改进为吸能效果更好的直八角形截面（图17和表5），可以保证前纵梁前段在不过多增加壁厚的同时具有较好的吸能效果。

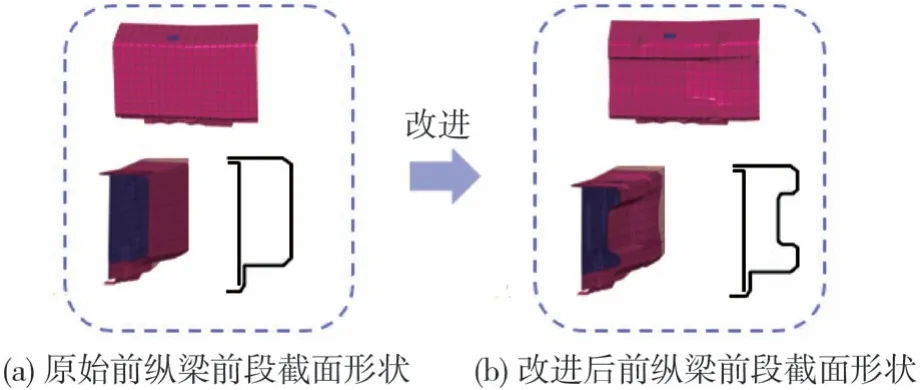
图17 改进前后的前纵梁前段结构对比

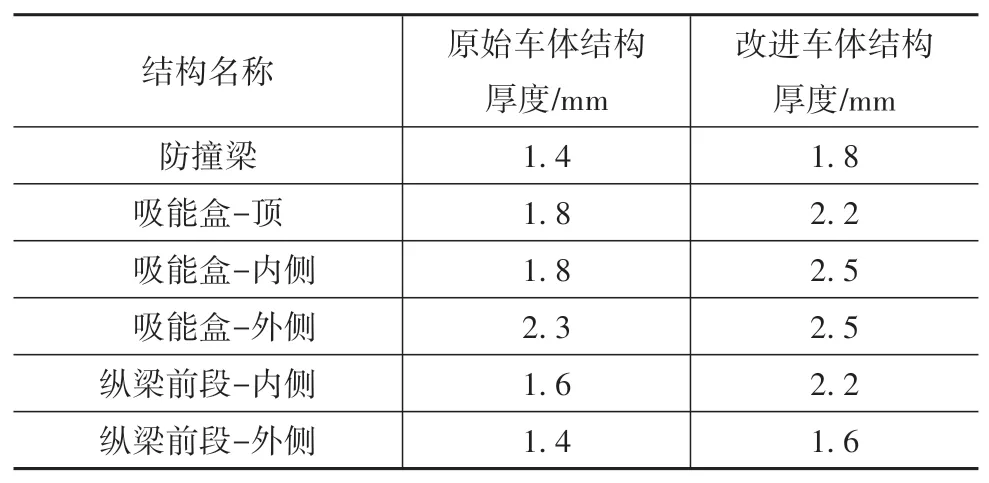
表5 改进前后的车体结构壁厚对比

要将原始碰撞波形的简化双台阶波的第2台阶改进为目标双台阶波的第2台阶，须降低原始波形第2台阶的高度，即须适当降低第2台阶波所对应的前纵梁中段和后段的两个主要车体吸能结构的刚度，以降低这部分车体结构在碰撞过程中产生的压溃反力。在不改变车体结构形状的前提下，适当减小结构壁厚能够使结构的刚度和碰撞过程中产生的压溃力降低。结构不同的变形模式也对压溃反力有很大影响，与压溃变形相比，薄壁梁发生弯曲变形时的压溃反力较小。对于前纵梁中段和后段处，纵梁的内侧与外侧采用不同壁厚，能诱导该部分结构在压溃过程中按照预想的变形模式产生变形吸能［11］。本文中对于前纵梁中段和后段结构进行改进时，将纵梁外侧的壁厚设计为小于内侧壁厚（表6），以诱导前纵梁中段和后段在压溃过程中发生向外侧弯折的弯曲形变。

表6 改进前后的车体结构壁厚对比

经过上述对于车体前端主要吸能结构的改进，利用LS-DYNA对改进后整车有限元模型进行正面100%刚性壁障碰撞仿真，可以得到改进后车体结构的碰撞波形和简化的双台阶波，如图18所示。对应的碰撞波形参数如表7所示。利用式（4）可算得车体结构改进后碰撞波形的评价指标，经计算改进车体结构后的碰撞波形评价指标γ=0.16，与目标波形的评级指标相等，满足改进要求。

图18 改进车体结构后的碰撞波形

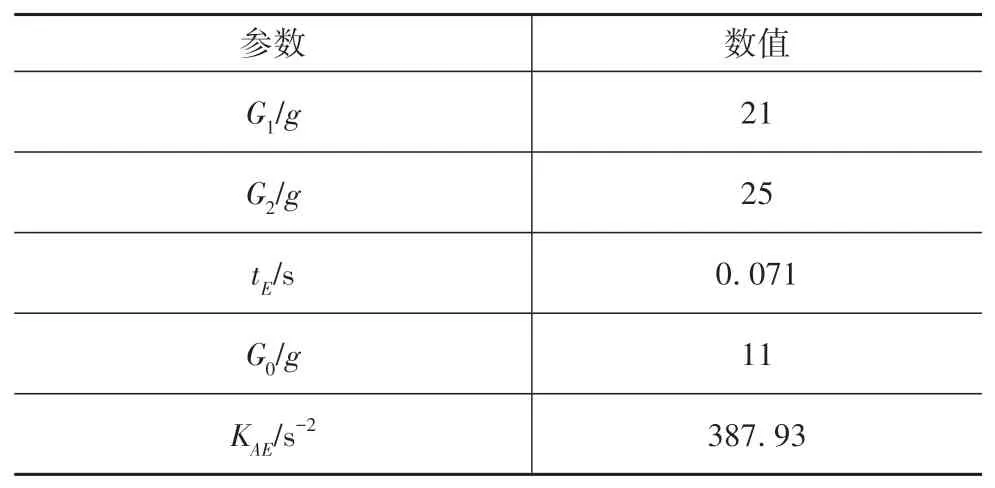
表7 改进车体结构后的碰撞波形耦合评价参数

3.2.3 约束系统改进设计

本次约束系统匹配改进设计依托于已有耦合数据库进行［7］。本次选取评价指标为0.13的三线性约束刚度曲线，目标参数为k1=340g/m、k2=180g/m、GL=26g，所对应的约束系统参数为安全带伸长率14%，限力3 800 N，安全气囊充气质量0.027 g，泄气孔直径34 mm。以图18中的改进碰撞波形为输入，将改进后的约束系统参数代入图10所示的MADYMO模型中进行仿真，最终获得的乘员加速度-相对位移曲线和其简化的约束刚度曲线如图19所示。改进前后的乘员伤害指标和碰撞星级的对比如表8所示。

图19 改进后三线性约束系统刚度曲线

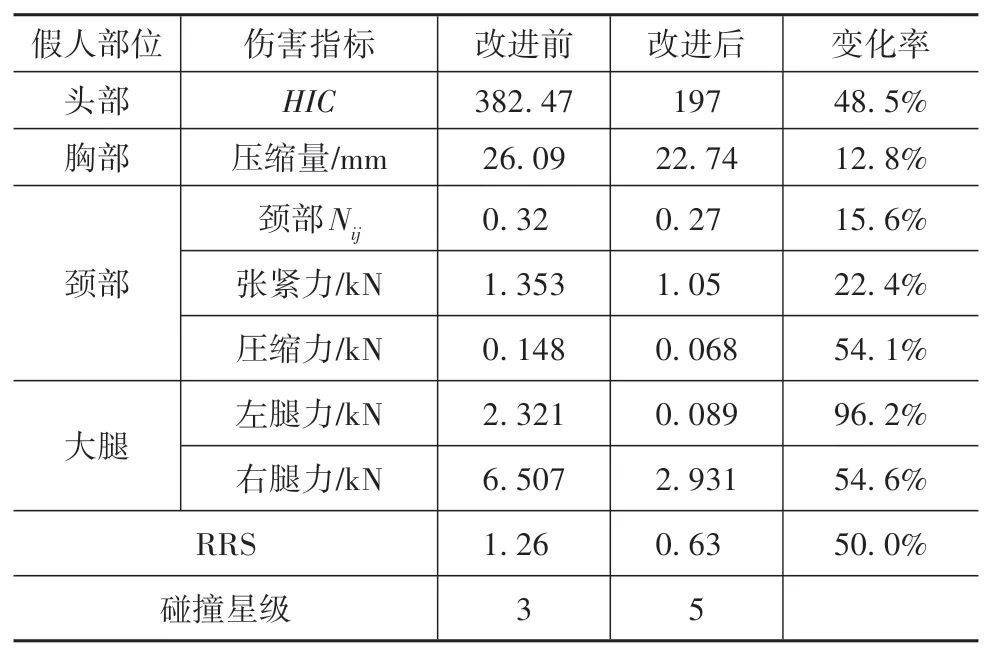
表8 改进前后正面碰撞驾驶员假人评定结果对比

4 结论

应用碰撞波形与约束系统特性耦合关系评价方法，对W5车型的碰撞波形、约束系统特性和两者之间耦合关系进行评价，找到了W5车型设计薄弱环节，考虑工艺、成本等因素对相关车体结构和约束系统进行改进设计。结果表明，利用耦合评价方法一方面可以帮助对现有车型进行星级预估，同时也可作为新车或已有车型改型设计的目标设计依据。

以改进后的碰撞波形为输入，通过调整安全带织带刚度、限力等级、安全气囊充气质量和泄气孔尺寸等参数进行了约束系统改进。最终改进方案使头部HIC、颈部压缩力、腿部轴向力等乘员伤害指标降低了约50%，胸部压缩量、颈部Nij和颈部张紧力降低了约15%，碰撞星级从三星提高到五星，有效提高了整车安全性。