积分迭代模式优化对侧翻一步碰撞算法的改进*

陈轶嵩，陈子童，王 童，刘永涛，罗 耿

（长安大学汽车学院，西安710064）

前言

我国综合国力不断提升，人均可支配收入逐年攀升，汽车保有量持续增长，逐渐成为家庭生活必需品，极大促进了汽车工业发展［1］。但与此同时城市交通状况也越发拥堵，大气环境污染进一步恶化，要求我们大力发展公共交通［2］。随着公路客运蓬勃发展，城市公交车及客运大巴是人民短途出行优选的交通工具［3］；但一些恶劣客车交通事故也时有发生。由于客车载客量较大，一次事故动辄造成大量人员伤亡，带来巨大损失，其中客车侧翻死亡率最高，危害极大。如何提高客车侧翻安全性，保护驾驶员及乘员生命安全，已成为世界各国研究人员亟待解决的迫切任务［4］。

客车侧翻一步碰撞算法是作者参考板料冲压一步成型算法思想［5］，提出的一种用于客车侧翻碰撞模拟分析的新算法。对于板料冲压一步成型算法，Batoz等［6］在1989年开始提出“逆方法”，对冲压件厚度及应力分布进行了预测；柳玉起等［7］对应用一步逆有限元法模拟冲压成形过程中的褶皱、回弹及失稳问题进行了研究；陈伟等［8］又在金属板料冲压一步逆成形算法的基础上，初步探讨了更具工程应用前景的“一步正”板料成形模拟算法，快速进行金属板料冲压成形性能评价，并收到了良好效果。借鉴该算法核心思想，客车侧翻一步碰撞算法同样基于非线性全量理论，利用了侧翻碰撞过程中能量转换关系，与现有LS⁃DYNA等增量法软件相比，在略牺牲一些计算精度情况下，大幅提升了模拟效率。

现有初始算法是对基于全量理论的侧翻一步碰撞理论体系的初步探讨，计算精度和效率仍有一定的改进空间。为进一步提高算法计算效率且保证精度，使算法能更好预测客车结构侧翻安全性，为后续对客车车身结构进行基于侧翻安全的拓扑优化提供支撑，本文中在客车侧翻一步碰撞初始算法基础上，分析算法运行过程中的关键环节，从计算量较大的积分和迭代部分入手，对初始算法积分和迭代方法进行探索和改进。首先，对算法单元积分方法，在单元厚度方向（下简称厚向）采用不同积分点数量并引入面内减缩积分和局部减缩积分，对厚向及面内积分点模式进行合理匹配，寻找算法能量和失衡力平衡迭代计算过程中最优积分方案。其次，对广义失衡力平衡迭代，采用更优的力与力矩分离迭代法，确定合理权重比，对力与力矩进行加权，提高迭代速度，完成迭代优化。改进后算法可在车身设计初期，对结构侧翻碰撞安全性进行快速评价，缩短产品开发周期，同时，可为后续针对客车侧翻安全性的灵敏度分析、参数优化和拓扑优化算法研究提供必要的支撑条件。

1 侧翻一步碰撞算法基本理论

客车侧翻一步碰撞算法，基于非线性全量理论和比例加载假定，依据ECE R66法规［9-10］，忽略中间状态和构形变化［11］，只考虑结构碰撞开始和最大变形两个状态。根据车体侧翻碰撞过程运动变形特点和能量转换关系，得到满足变形条件初始解，采用Newton⁃Raphson法迭代求解［12］，快速获得结构最终变形。

将碰撞开始状态结构作为初始构形{X0}。此时车体未发生变形，结构动能Ed为

式中：M为车体质量；Δh为车体质心下降高度；J为车体绕侧翻假定转轴的转动惯量；ω为车体角速度。

碰撞开始状态结构各节点速度{v0}由式（2）计算：

式中：ri为各节点到侧翻假定转轴距离；n为节点数。

在结构最大变形状态，车体结构产生明显变形。侧翻一步碰撞算法中，结构最大变形不确定须假定一个最大变形构形{x0}。各节点位移{U0}由式（3）计算：

车体动能Ed在碰撞中主要转换为结构形变能，结构形变能W由式（4）计算［13］：

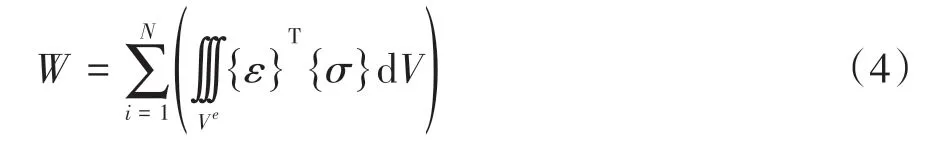
式中：{ε}为单元塑性应变；{σ}为单元塑性应力；Ve为单元体积；N为单元数。

结构形变能W与车体动能Ed理应相等，即

若式（5）不满足，则对节点位移{U0}进行修正，按照式（4）重新计算结构形变能。将满足式（5）能量关系假定的节点位移{U}作为Newton⁃Raphson迭代初始解。

对满足能量转换关系初始解{U}，节点失衡力{R(U)}已处于不平衡状态：

应用Newton⁃Raphson法，解决节点失衡力不平衡问题。对初始解{U}按式（7）迭代求解，使式（6）达到平衡，得到结构最终变形。

2 单元积分点模式优化

侧翻一步碰撞初始算法采用Mindlin壳单元厚向五点且面内全积分方案，为在基本保证计算精度基础上进一步提高计算效率，本文在积分方案上做进一步研究。单元面内，在四点全积分基础上，引入减缩积分和局部减缩积分方案；单元厚向，引入五点、七点和九点3种高斯积分方案；并在厚向各积分层采用减缩积分与局部减缩积分的不同匹配方案。经多次研究对比发现，薄壳单元中性层积分点数量对模拟结果影响较大，且中性层局部减缩积分方案具有更高的计算精度。因此，为保证一定精度，本文中所有积分方案均采用在中性层面内应用局部减缩积分方式进行匹配，同时为保证计算效率提升效果，每个积分方案中其余积分层最多引入两层局部减缩积分。

2.1 单元面内积分方案

面内减缩积分即单点高斯积分，计算效率较高，可避免使用全积分导致刚度过大及剪切锁死问题，但数学上看，计算精度相对较低，其积分点位置和积分系数为

式中：r、s为积分点坐标；h为积分系数；i=1，j=1。

本文中所提局部减缩积分是一种复合式积分方法，即利用单点积分计算内力中切应力相关分量，利用四点积分计算正应力相关分量，既可克服单点积分引起的沙漏模式，又可避免四点积分引起的剪切锁死。

为实现局部减缩积分，将单元［B］矩阵和应力向量{σ}进行分解，令：

其中

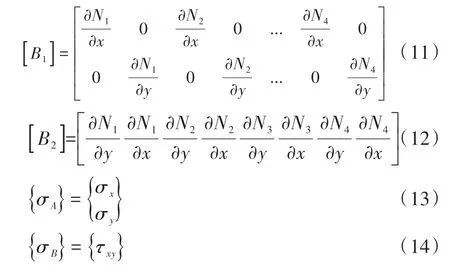
单元内力为

令：

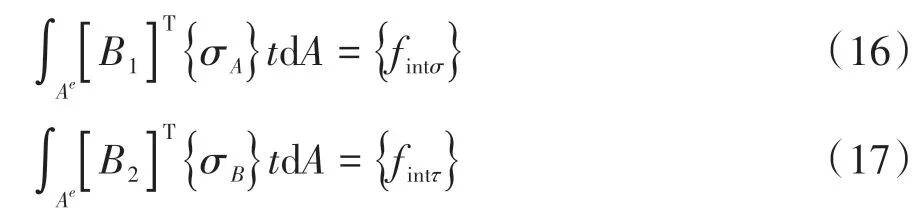
式中：{fintσ}为只与正应力σx和σy的相关项，数值求解时，为提高计算精度，沿r、s方向均取2点积分；{fintτ}为只与切应力τxy的相关项，为避免剪切锁死，求解时采用单点减缩积分，即

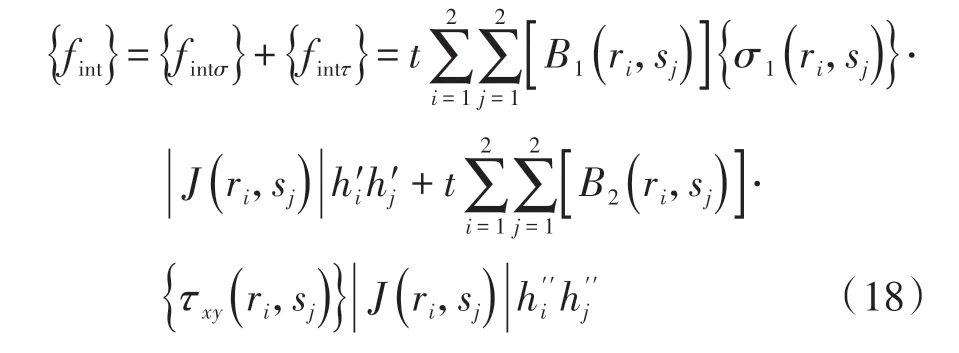
2.2 单元厚向积分方案

2.2.1 厚向五点高斯积分

当厚向采用五点高斯积分时，各单元厚向积分点位置如图1所示。1点到5点的高斯积分点位置因子分别为0.906 179 85、0.538 469 31、0、-0.538 469 31、-0.906 179 85，对应的积分系数分别 为0.236 926 89、0.478 628 67、0.568 888 89、0.478 628 67、0.236 926 89。

图1 单元厚向五点积分示意图

同时，考虑到积分方案对中性层对称性设计，单元厚向五点积分各积分层面内减缩积分与局部减缩积分匹配方案设计如表1所示。

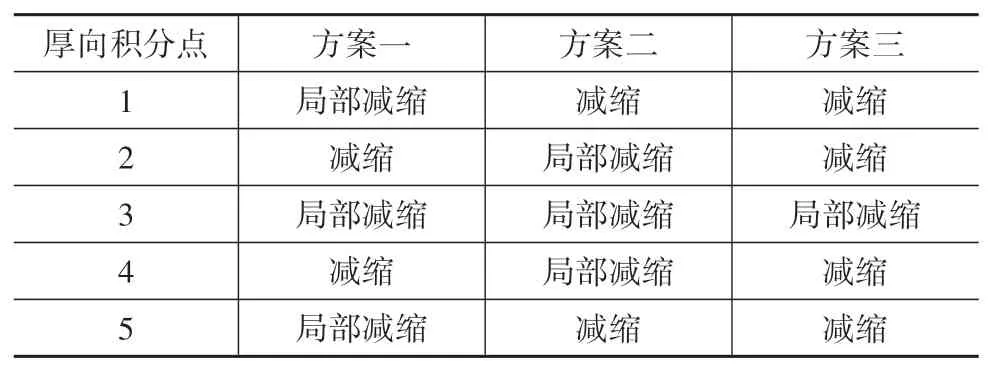
表1 厚向五点高斯积分方案

以某客车车身段模型作为分析对象，将厚向五点各积分方案应用于客车侧翻一步碰撞快速算法进行计算，获得车身段两侧立柱各测点变形量和模拟时间，并与LS⁃DYNA计算结果对比，车身段封闭环两侧立柱各测点变形量对比的柱状图如图2所示。

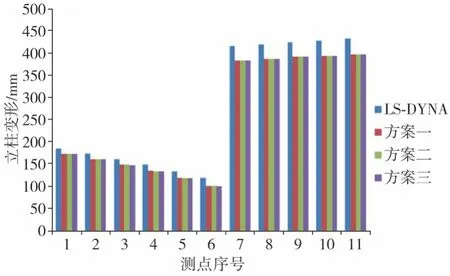
图2 厚向五点高斯积分与LS⁃DYNA测点变形量对比

接着，对应用厚向五点3个积分方案分析计算时间与LS⁃DYNA时间进行对比，结果如表2所示。

表2 厚向五点高斯积分与LS⁃DYNA分析效率对比

本文中选取11个测点变形量作为评价指标，对算法计算精度进行考量。通过对比分析发现，计算精度上3种积分方案计算结果十分接近，与LS⁃DYNA计算结果平均相对误差分别为8.895%、8.996%和9.102%，方案三计算精度略低。计算效率上，3个积分方案模拟时间比LS⁃DYNA都有明显缩短，且方案三计算效率比前两个方案略有提高。

2.2.2 厚向七点高斯积分

当单元厚向采用七点积分时，随着单元厚向积分点数的增加，其积分方案的匹配方式也有所增加，共设计4种积分方案。单元厚向七点积分各积分层面内减缩积分与局部减缩积分的匹配方案设计如表3所示。

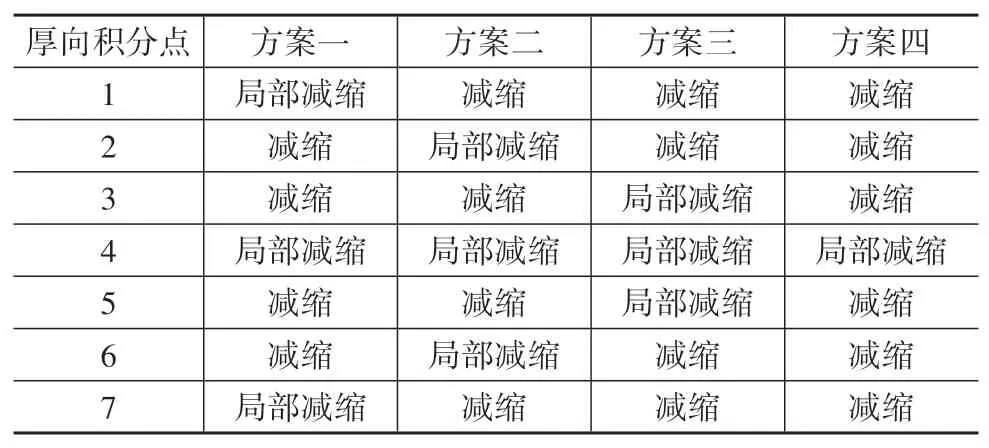
表3 厚向七点高斯积分方案

厚向七点积分与图1中所示的单元厚向五点积分示意图类似，只是积分点数量和位置有所不同。厚向七点积分中积分点1到积分点7的高斯积分点位置因子分别为0.949 107 91、0.741 531 19、0.405 845 15、0、-0.405 845 15、-0.741 531 19、-0.949 107 91，对应的积分系数分别为0.101 228 54、0.279 705 39、0.381 830 05、0.417 959 18、0.381 830 05、0.279 705 39、0.101 228 54。

同样，将厚向七点各积分方案应用于客车侧翻一步碰撞快速算法进行改进，获得封闭环两侧立柱各测点变形量及计算时间，对比结果如图3所示。

图3 厚向七点高斯积分与LS⁃DYNA测点变形量对比

接着，将厚向七点4个积分方案计算时间与LS⁃DYNA分析所用时间进行对比，确定各方案计算效率优劣，结果如表4所示。

表4 厚向七点高斯积分与LS⁃DYNA分析效率对比

同样，以11个测点变形量平均相对误差作为每个积分方案算法计算精度的评价标准。通过误差计算和对比发现，在计算精度上厚向七点4种积分方案计算结果与LS⁃DYNA平均相对误差分别为3.278%、3.675%、3.667%、4.087%，方案一计算精度最高，方案二和方案三计算精度相差不多，方案四计算精度比前3个方案有所降低。在计算效率上，4个方案模拟时间相差不多，比LS⁃DYNA仍有明显缩短。与厚向五点积分相比，计算精度提高较大，计算效率略微降低。

2.2.3 厚向九点高斯积分

当单元厚向采用九点积分时，随着单元厚向积分点数进一步增加，其积分方案匹配方式继续增加，共设计5种单元积分方案。单元厚向九点积分各积分层面内减缩积分与局部减缩积分匹配方案设计如表5所示。

表5 厚向九点高斯积分方案

厚向九点积分与图1中所示的单元厚向五点积分示意图类似，只是积分点数量达到9个。厚向九点积分中积分点1到积分点9的高斯积分点位置因子分别为0.968 160 24、0.836 031 11、0.613 371 43、0.324 253 42、0、-0.324 253 42、-0.613 371 43、-0.836 031 11、-0.968 160 24，对应的积分系数分别 为0.081 274 39、0.180 648 16、0.260 610 69、0.312 347 08、0.330 239 36、0.312 347 08、0.260 610 69、0.180 648 16、0.081 274 39。

同样，将厚向九点各积分方案应用于客车侧翻一步碰撞快速算法进行改进，获得封闭环两侧立柱各测点变形量和计算时间。统计各方案中11个测点变形量数据，将厚向九点各积分方案计算结果与LS⁃DYNA结果进行对比，封闭环两侧立柱各测点变形量对比柱状图如图4所示。

图4 厚向九点高斯积分与LS⁃DYNA测点变形量对比

接着，将厚向九点5个积分方案计算时间与LS⁃DYNA进行对比，确定各方案计算效率优劣，结果如表6所示。

表6 厚向九点高斯积分与LS⁃DYNA分析效率对比

同样，以11个测点变形量平均相对误差作为每个积分方案算法计算精度评价标准。通过误差计算和对比分析发现，在计算精度上厚向九点5种方案计算结果与LS⁃DYNA平均相对误差分别为2.868%、2.927%、3.032%、3.038%、3.210%，方案一计算精度稍好，方案五计算精度比前4个方案略低。在计算效率上，方案五计算效率比前4个方案略有提高，比LS⁃DYNA仍有明显缩短。对比五点、七点积分来说效率下降较为明显，且比厚向七点积分精度提高并不明显。

综合对比以上结果可知，随着厚向积分点个数增加，计算精度逐步提高，但计算效率相应下降。从上述分析可看出，厚向七点积分方案一具有较高计算精度，满足算法精度要求，同时由于减缩积分和局部减缩积分引入，使其具有较高计算效率。综合考虑精度与效率，本文最终确定厚向七点积分中方案一作为初始算法改进积分方案。

3 广义失衡力迭代模式优化

客车侧翻碰撞变形复杂，单元除有面内拉压引起的面内变形，还有弯曲变形。侧翻一步碰撞初始算法迭代过程采用力和力矩融合迭代方式，没有引入比例系数进行调整，该迭代方式存在不合理性，忽略了两点：第一，力和力矩量纲不同，数值差别也较大，直接融合在一起进行计算失衡力“2”范数，会影响广义失衡力迭代收敛效率；第二，力和力矩对广义失衡力平衡迭代收敛效率贡献度也有所不同，不考虑权重直接进行迭代，同样会影响计算效率。故本文将力和力矩进行分离，分别计算各自失衡力“2”范数，取不同权重比对其进行加权调整，对侧翻一步碰撞算法进行改进。

首先，将计算得到的Mindlin组合壳单元节点广义内力，由式（19）表示：

接着，计算各节点广义失衡力向量R(ui)，如式（20）所示：

其中每个节点共包含3个失衡力Rix、Riy、Riz和3个失衡力矩Rixx、Riyy、Rizz，即

节点广义失衡力计算完成后，将每个节点中的失衡力分离出来单独计算失衡力“2”范数：

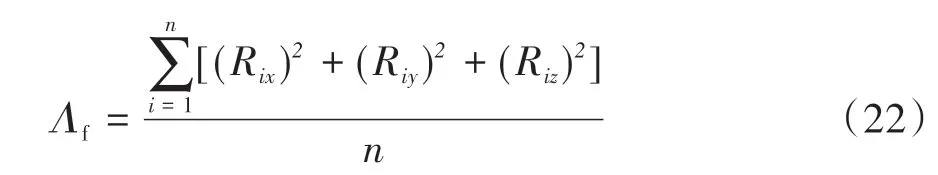
式中n为车体结构中单元节点总数。

同样，将每个节点中失衡力矩分离出来单独计算力矩“2”范数：

取一组权系数将上述力和力矩“2”范数进行整合，得到加权调整后的广义失衡力“2”范数，即

式中α、β分别为力和力矩的权系数，其和为2。

利用算得的结构变形情况初步判断计算结果能否满足工程计算的合理要求，统计不同权重比下算法的计算时间，绘制计算时间-权重比重线，如图5所示。通过选取曲线中计算时间较短的区段进行多项式拟合，并求得拟合曲线的极值确定合理权重比，以确定改进算法中力和力矩的合理权系数值。

图5 计算时间-权重比曲线

算法计算时间曲线开始时有一个较短的下降段，随后则逐渐上升，计算时间最短的区间段在权重比为0.11~1之间。通过对比计算，可确定计算时间最短的点所对应的权重比为0.479 2，故最后得到合理的权重值α、β分别为0.684和1.352［1］。

选取合适松弛因子，利用式（7）中迭代过程对广义失衡力进行迭代，在每步迭代中，均需对比式（20）中所示广义失衡力“2”范数的大小，直到达到最小值时结束迭代，即

此时，车体结构处于稳定状态，该状态下车体结构变形即为客车侧翻碰撞后的结构最终变形。

4 应用实例

为检验单元积分点模式和广义失衡力迭代模式优化改进后侧翻一步碰撞改进算法的有效性，本文中选取某12 m公路客车车身结构典型车身段作为研究对象。利用改进算法对该车身段进行侧翻碰撞分析，将计算结果与初始算法、LS⁃DYNA和侧翻试验结果进行精度及效率对比。

4.1 模型建立

车身段侧翻试验参考欧洲ECE R66法规设计，试验台高800 mm，试验模型配重后质量2 409 kg，质心高度1.5 m，典型车身段试验模型如图6所示。

图6 典型车身段模型示意图

对该车身段试验模型进行简化并假设，建立车身段有限元模型如图7所示。模型共离散270 171个单元，269 894个节点，骨架钢材选用Q345钢，材料弹性模量E=2.06×1011Pa，泊松比μ=0.3，密度ρ=7800 kg/m3，屈服强度σs=345 MPa。

图7 车身段有限元模型

车身段侧翻试验模型以及相应的有限元模型中所包含的A、B两个封闭环，参考企业侧翻试验过程中测点选取方式，在封闭环两侧立柱共选取11个测点，左侧立柱内表面选取6个测点，间隔100 mm，右侧立柱内表面选取5个测点，间隔100 mm，各测点具体位置见图8。

图8 封闭环模型测点选取方式示意图

将有限元模型导入LS⁃DYNA求解计算，两侧立柱各测点变形量柱状图如图9所示。

图9 封闭环模型LS⁃DYNA分析测点变形量柱状图

4.2 结果对比

初始算法结构变形情况如图10所示，改进算法结构变形情况如图11所示，LS⁃DYNA分析结构变形情况如图12所示。

图10 初始算法结构变形情况

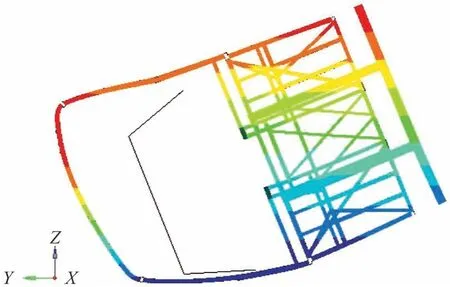
图12 LS⁃DYNA结构变形情况

由图10和图11可看出，两种算法结构变形趋势一致性良好，改进算法具有基本工程计算合理性。为对改进算法计算精度进行更准确分析，需对各测点变形量进行定量对比。

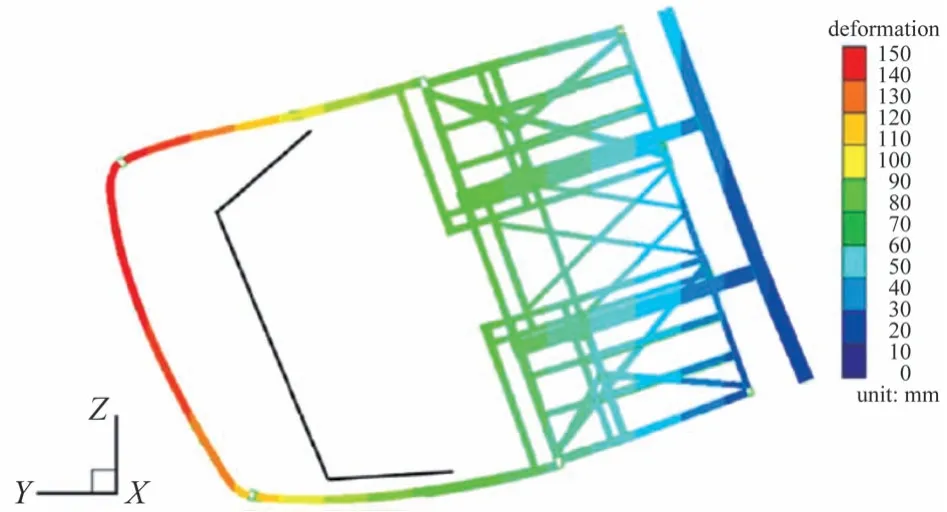
图11 改进算法结构变形情况

侧翻试验测点变形量数据来自企业实车开发过程中车身段侧翻试验，数据由企业技术人员协助测得。侧翻试验、LS⁃DYNA分析、初始算法和改进算法所得封闭环A、B两侧立柱变形量数据统计如表6所示。

表6 典型车身段测点变形量统计 mm

封闭环A两侧立柱各测点变形量对比见图13，封闭环B两侧立柱各测点变形量对比如图14所示。

图13 封闭环A各测点变形量对比

图14 封闭环B各测点变形量对比

通过对比分析发现，改进算法与LS⁃DYNA平均误差为2.291%，初始算法与LS⁃DYNA平均误差为3.37%；改进算法与侧翻试验平均误差为10.349%，初始算法与侧翻试验的平均误差为10.765%。可以认为，改进算法在计算精度上有所提升，且小于工程有限元仿真分析误差容许值15%，基本满足算法所需计算精度。

接着，对计算效率进行对比，结果如表7所示。

表7 计算效率对比

可以看出，改进算法计算效率在基本保证精度的情况下明显提高，检验了本文所提改进方法在实际应用中的有效性。

5 结论

为进一步提高侧翻一步碰撞算法计算效率且保证计算精度，为后续对客车车身结构进行基于侧翻安全的拓扑优化提供支撑，在客车侧翻一步碰撞初始算法基础上，分析算法运行过程中的关键环节，从计算量较大的积分及迭代部分入手，对初始算法积分及迭代方法进行探索和改进。经过计算分析，改进算法在基本保证计算精度的同时，计算效率得到显著提升。本文中所提单元积分点模式及广义失衡力迭代模式改进方案，具有良好应用效果。

但是，初始算法本身单元模型基于Mindlin壳单元，受单元模型理论限制，算法计算精度不能大幅提升，后续仍需对算法单元模型进行改进研究，进一步提升算法计算精度和效率，以便在车身设计初期，对结构侧翻碰撞安全性进行更加快速准确评价，进一步缩短产品开发周期，为后续针对客车侧翻安全性的灵敏度分析、参数优化和拓扑优化算法研究奠定基础。