数学学案如何选择课前、课中、课后试题

杜艳丽

摘要：科学地设计和使用学案，对于学案教学来说尤为重要。作为学案中的大块头——课前、课中、课后试题的选择，更是关系到一节学案课是否成功。因此，教师应以学生的发展为出发点，关注学情，合理设计课前、课中、课后试题。

关键词：数学学案;课前;课中;课后

作为体现新课改精神的教学方式，学案教学正越来越多地呈现出其引领课堂教学的独特优势和价值。因此，科学地设计和使用学案对于学案教学来说就显得尤为重要。那么，作为学案中的大块头——课前、课中、课后试题的选择，就成为关系到一节学案课是否成功的主要因素。

如何选择课前、课中、课后试题？我认为，应以学生的发展为出发点，关注学情，尊重学生的意见;在布置课前学习时，应对重、难点问题有基本的了解与思考，应联系新旧知识做好学习铺垫，也可采取留空式知识建构及思考探究题形式;在课堂学习中，探究问题的设计要突出方法引导、能力提升，同时对检测评价题做到精选;课后训练应体现难度层次的递进，让学生按照自己的能力水平，不同程度地完成训练，使每个学生都有自己的收获，从而激发学生的学习积极性;学案的最后应预留部分空间，让学生及时进行自我学习反思，这也是补偿学习和教学的重要资源。

一、课前试题的选择应遵循的原则

（一）基础性原则

课前习题要体现“双基”，即基础知识和基本能力。题目的设计要从基本知识入手，学生通过完成课前习题达到掌握基础知识、形成基本能力的目的。

（二）层次性原则

设计课前习题要根据学生的认识活动规律，由浅入深，由易到难，要有梯度，这样才能为学生能力的发展和提升创造更广阔的空间。

（三）探究性原则

《义务教育数学课程标准》指出：“让学生亲身经历将实际问题抽象成数学模型并进行解释与应用。”换言之，要让学生了解知识的产生、发展，让他们自主探究发现问题，完成知识的构建，从而使学生不仅能够解决问题，而且从中体验数学知识本身所蕴含的数学文化、数学情感的魅力。所以，教师在设计习题时，要充分融入探究的元素。

（四）趣味性原则

很多的数学知识都是枯燥乏味的，这时我们可以加入一些生活的、游戏的元素，让题目更能吸引学生的眼球。

（五）思想性原则

数学是思维的体操。数学教学的一个重要任务是让学生理解并应用数学思想、方法。在设计课前习题的时候，教师要有意识地渗透，久而久之，学生才能从本质上提高数学水平，增强解决问题的能力。

例如，人教版七年级下册数学7.3“多边形及其内角和”的学案，课前试题是这样呈现的：

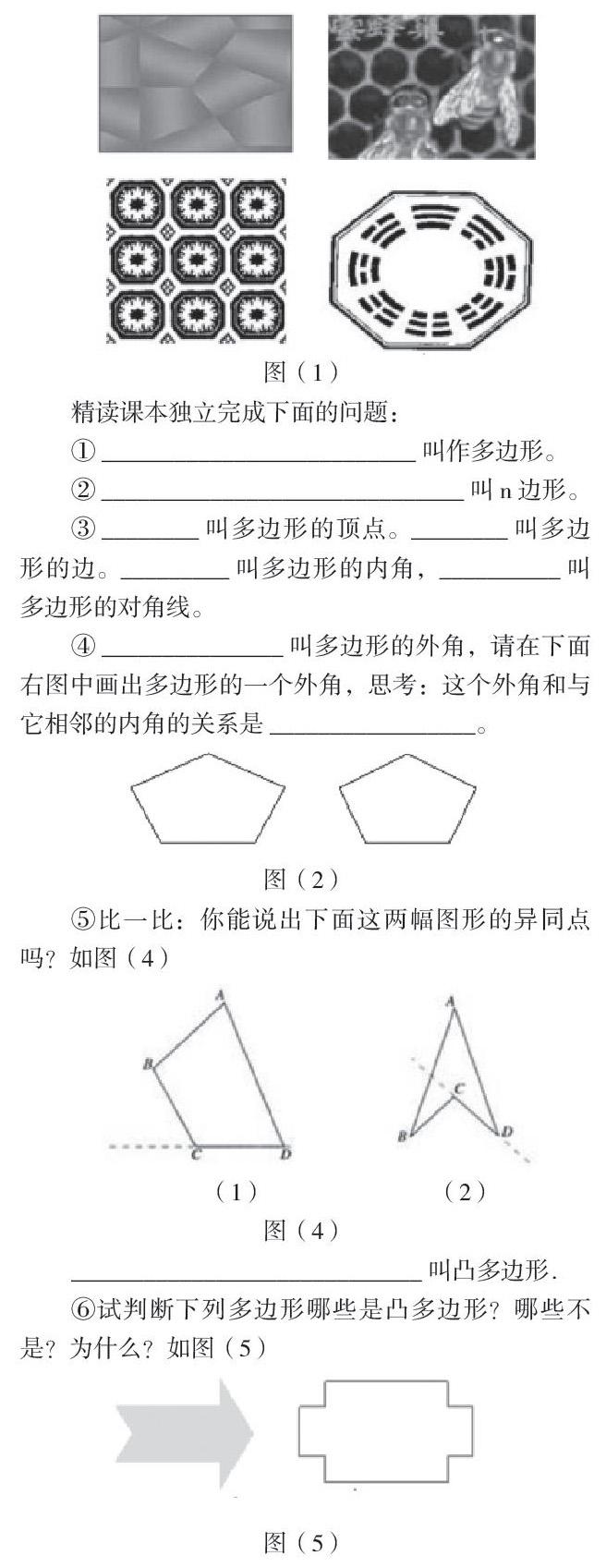
出示课本的图7.3-1

问题：你能从中找出几个由一些线段围成的平面图形吗？如图（1）

精读课本独立完成下面的问题：

①__________________________叫作多边形。

②______________________________叫n边形。

③________叫多边形的顶点。________叫多边形的边。_________叫多边形的内角，__________叫多边形的对角线。

④_______________叫多边形的外角，请在下面右图中画出多边形的一个外角，思考：这个外角和与它相邻的内角的关系是_________________。

⑤比一比：你能说出下面这两幅图形的异同点吗？如图（4）

_____________________________叫凸多边形.

⑥试判断下列多边形哪些是凸多边形？哪些不是？为什么？如图（5）

在课堂上合理地使用学案，教師要真正地进行“二次备课”，处理好学案教学过程中的问题。课堂教学是“用学案”，而不是“讲学案”。在学案中体现学生的主体地位，应在教师的有效指导下实现。那么，要想真正在学案中体现学生的主体地位，教师应科学地选择课中试题。

二、课中试题的选择应遵循的原则

（一）目的性原则

课中习题必须目的明确，做到“有的放矢”。

（二）层次性原则

课中习题既要考虑知识结构的层次性，又要考虑学生的认知水平，要使好、中、差三类学生都能获得练习的最佳效果。

（三）启发性原则

课中习题必须能够启发学生积极思维，调动学习积极性。

（四）多样性原则

课中习题必须形式多样，能吸引学生的注意力、激发学生的兴趣。

（五）少、精、活原则

课中习题不是越多越好，而是要少而精、少而活，具有典型性。

例如，人教版七年级下册数学7.3“多边形及其内角和”的学案，课中试题是这样呈现的：

1.判断题

（1）任意一个三角形的三条高，至少有一条在此三角形内部（   ）

（2） 一个多边形从一个顶点共引出三条对角线，此多边形一定是五边形 （    ）

（3）一个三角形内角之比为3：2：1，此三角形为钝角三角形（ ）

（4）多边形中的内角，最多有2个是锐角（ ）

（5）一个三角形中，至少有一个角不小于60度（）

2.选择题

（1）一个多边形的内角和是720°，这个多边形的边数是

A. 4     B.  5     C. 6      D.  7

（2）正八边形的每个内角为（   ）

A.120°   B.135°   C.140°  D.144°

（3）如图，已知矩形ABCD ，一条直线将该矩形 ABCD 分割成两个多边形，若这两个多边形的内角和分别为 M 和 N ，则 M + N 不可能是（      ）

A . 360      B . 540    C. 720     D . 630

（4）若n凸边形的内角和为1260°，则从一个顶点出发引的对角线条数是____

3.解答题

（1）O为四边形ABCD内一点，如果连接OA、OB、OC、OD，可以得几个三角形？它与边数有何关系？

（2）O在五边形ABCDE的AB上，如果连接OC、OD、OE，可以得到几个三角形？它与边数有何关系？

在数学教学中，学习数学基本知识是基础，形成数学思想并运用数学知识解决实际问题是目的。学案中的课后训练，一方面要注重基础知识的学习和巩固，另一方面要注重对学生进行基本技能的训练，让知识转化为技能。只有两者兼顾，才能真正让学生把已经掌握的知识和形成的技能技巧运用到学习过程中去，使之达到“点石成金”的目的。

三、课后训练应遵循的原则

（一）基本性原则

这类题通常分三个层次：一是复述新知的原理和方法，二是模仿性的个别训练，三是单项集中练习。其目的是巩固新知的原理和方法，使学生初步形成技能。

（二）灵活性原则

这是变换非本质属性设计的，目的是从不同的侧面揭示知识的本质，加深学生对知识的理解。

（三）综合性原则

这是把几个单项练习有机地结合起来，目的是帮助学生沟通知识之间的内在联系，形成良好的认知结构，提高解题的灵活性，培养学生的数学思维能力、应用能力。

（四）系统性原则

这是根据教学需要，按一定的逻辑体系，把学过的各类知识有机组合而设计的练习，其目的是帮助学生系统整理知识、完善认知结构。

（五）检测性原则

反馈调节教学过程，检测评价教学效果，从而达到“堂堂清”的目的。

例如，人教版七年级下册数学7.3“多边形及其内角和”的学案，课后试题4是这样呈现的：

4.思考论证

同学们，你们会用画多边形的对角线来解决生活中的数学问题吗？

比如，学校举办足球赛，共有5个班级的足球队参加比赛，每个队都要和其他各队比赛一场，根据积分排列名次。那么，学校一共要安排多少场比赛？

姣姣、林林、可可、飞飞、红红和娜娜6人参加一次会议，见面时他们相互握手问好。已知姣姣已握了5次手，林林已握了4次手，可可已握了3次手，飛飞已握了2次手，红红握手1次，请推算出娜娜目前已和哪几个人握了手。

数学就是要研究客观规律，把其运用于实际。数学题千千万万，学案中习题的选择要走出贪多、贪全的误区。习题的选择一定要典型，不但要注意到知识点的覆盖面，还要让学生能通过训练掌握规律，达到“以一当十”的目的。

参考文献：

[1] 蔡美玉 . 现代多媒体技术在小学数学课堂教学中的应用 [J]. 学周刊 ，2017（19）.

[2] 董立花 . 利用多媒体技术提高小学数学课堂教学效果 [J]. 学周刊 ，2017（36）.

（责任编辑：奚春皓）