自适应VMD-FSK对低速重载下的转轴裂纹诊断*

司呈鑫，章翔峰，姜 宏，马铜伟，申 勇

(新疆大学机械工程学院，乌鲁木齐 830047)

0 引言

转轴作为旋转机械的核心部件，是故障的高发部位[1]；转轴在低速承受巨大载荷时，故障特征频率极低、振动能量小，在诊断过程中很容易忽视[2]。如不及时进行诊断，很容易发生事故。因此对转轴运行时的故障诊断具有重要的工程意义[3]。

在微弱故障特征提取的研究中，文献[4]提出经验模态分解( empirical mode decomposition，EMD)，EMD算法适用于非平稳信号的处理，文献[5]将EMD算法用于对旋转机械的故障信号的时频分析研究，取得了较好的分析效果；为了得到轴承不同的故障类型特征，文献[6]将EMD与最大峭度解卷积方法进行联合分析，但是EMD算法存在模态混叠和端点效应[7]。文献[8]对EMD进行改进, 提出通过IEMD与支持向量机结合的方法，成功识别出多个故障。进一步的，文献[9]提出变分模态分解( variational mode decomposition，VMD)方法，有效地抑制了EMD算法存在的模态混叠现象；VMD算法将信号的分解过程转换为变分模型的构造与求解，有效地抑制了各分量之分解为中心频率和带宽不同的各分量，非常适用于多分量非平稳非线性信号的分离[10],文献[11]采用VMD结合散布熵成功的提取出了轴承的故障信息。但是VMD分解时需要考虑到分解模态个数及惩罚因子之间的相互影响。文献[12]通过中心频率法来确定VMD算法中分解模态参数K值，并结合快速谱峭度，实现了对滚动轴承早期故障的诊断；文献[13]利用EMD来估计VMD算法中的分解个数，对仿真和实测数据处理，都取得了理想的诊断效果；文献[14]利用VMD对轴承早期微弱故障进行诊断，并通过瞬时频率均值判断法确定模态参数K的取值，成功诊断出故障特征。

在上述研究的基础上，本文提出利用粒子群算法对VMD的参数[K,α]进行优化，对低速重载下转轴裂纹故障频率进行识别提取。为验证该方法的有效性，首先获得含裂纹转轴系统仿真信号，其次利用自适应VMD将故障信号分解为中心频率不同的各IMF分量。由相关系数法得到最佳分量，利用FSK对最优分量进行滤波处理，将包络谱中的频率成分，与故障频率分析对比，验证方法的有效性。最后仿真与实验证明该方法可以准确地将低速重载下转轴裂纹的特征频率提取出来。

1 变分模态分解

变分模态分解能够对复杂多分量信号进行分解，并将x(t)分解为一系列本质模式函数ck(t)，这些本质模式函数在它们各自的中心频率附近带宽有限。通过这些本质模式函数重构信号。算法在频域内迭代更新各个本质模式函数ck(t)，将本质模式函数频谱的重心作为中心频率wk。VMD算法的实现包括约束变分模式的构造和求解两个过程。具体步骤如下:

(2)更新ck(t)和ωk；

(1)

(2)

(3)用式(3)更新λ;

(3)

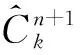
(4) 规定判定精度ε>0,如果

(4)

迭代停止，否则返回步骤(2)。

2 基于粒子群优化的变分模态分解

对信号使用VMD算法进行处理时，需要对惩罚因子α和分解参数K进行提前设定，不同的K值和α值会造成不同的处理结果。算法中惩罚因子α越小，信号分解后的模态函数的带宽就会越大；反之亦然。一般的，分解个数与惩罚因子的选取难以确定，人工选取的参数很难保证其结果是否最优。针对于这种情况，本文通过寻优算法粒子群算法对分解个数与惩罚因子的参数组合进行优化，选取最优组合。

粒子群算法[15]优点突出，它具有良好的全局寻优能力。本文利用粒子群算法对分解个数与惩罚因子两个参数进行智能寻优，可实现分解模态参数K及惩罚项参数α的自适应筛选。可以避免人为主观因素带来的影响。

假设由N个粒子组成一个D维空间。种群为Y=(Y1,Y2,…,YN)，其中第i个粒子Yi=(yi1,yi2,…,yid)表示1个D维向量。粒子的速度为Vi=(vi1,vi2,…,vid)，其个体局部极值为Pi=(pi1,pi2,…,pid)，种群全局极值G=(g1,g2,…,gd)，粒子迭代更新自身速度和位置的公式表述为:

(5)

式中，ω表示惯性权重;d的值为1,2,…,D;i表示为 1,2,…,N;k是当前的迭代次数；C1和C2是加速度因子；η表示为随机数，它是介于[0,1]之间的。

转轴出现裂纹时的典型特征是出现周期性振动信号，不同于噪声信号，因此通过PSO算法优化参数时，选择的适应度函数需考虑信号的周期性。文献[16]中提出一种包络熵指标，该指标考虑到振动信号中故障信息的周期特性, 假定信号包络谱幅值X(j)(j=1，2，…，M)则指标Ep的数学表达式如下：

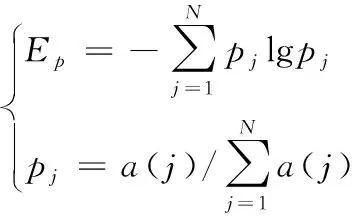
(6)

式中，pj为a(j)的归一化形式，a(j)为信号经Hilbert解调而得到的包络信号，包络熵Ep越小，表示信号解调后的周期性越好。当信号的周期特性越强时，包络熵值小，反之，信号周期特性不显著时，包络熵值大，鉴于此情况，把包络熵值最小化的情况当作寻优目标进行优化，整个优化过程如图1所示。

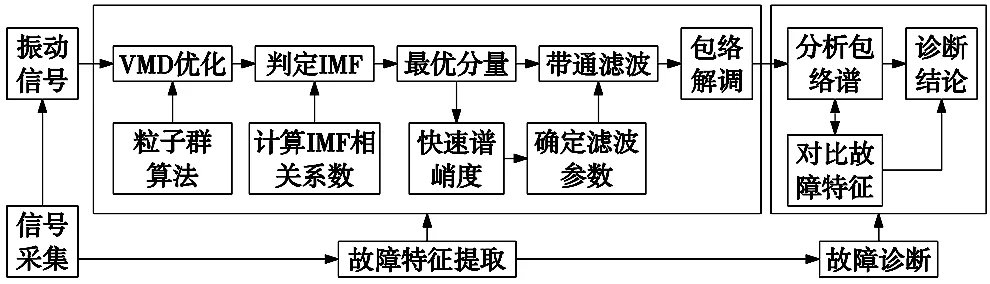
图1 自适应VMD+FSK转轴故障诊断流程

3 仿真信号分析

本文选取的故障类型为：输入转速为500 r/min、采样点数为3000点、采样频率为4096 Hz、转频为8.3 Hz、特征频率为8.3 Hz。图2为转轴含裂纹时仿真信号的时域图及包络谱，当转轴出现裂纹时，时域响应表现出明显的幅值调制现象，在时域图中呈现简谐波波形[17]。简谐波周期T的倒数1/T为转轴的转频；同时，由于转轴裂纹出现的呼吸效应，包络谱中一倍频幅值明显增高,造成的结果是在啮合频率处伴有明显的边频带[18]，但从包络谱中观察到，频率成分复杂导致无法直观地判断转轴出现了裂纹。

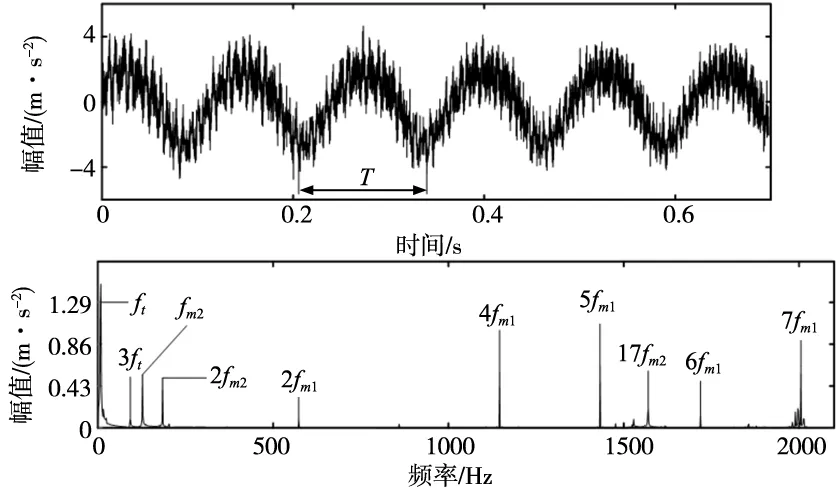
图2 含裂纹转轴时频域图

因此对低速重载下转轴裂纹信号进行VMD分解，但VMD分解之前，需要对分解模态参数K及惩罚项参数α进行合理设定。采用PSO对分解个数和惩罚系数组合进行寻优，如图3a所示，迭代到第4代时，极小包络熵4.623 551出现，极小包络熵优化得到的最佳影响参数组合为[7，3075]，设置VMD参数对振动信号进行分析，得到8个模态分量IMF1～IMF8，波形与所对应的频谱如图3b所示。然后由相关系数法得到最优分量为IMF3，利用快速谱峭度对最优分量计算并进行滤波处理，如图3d所示，得到Kmax=6.2、level=0、Bw=2 148.5 Hz、fc=1 074.25 Hz。根据图中显示的参数，直接对分量IMF3进行带通滤波并得到包络谱，如图3c所示，可以看出故障特征f(8.3 Hz)及其2倍、3倍频幅值突出，特征频率信息被准确提取，与转轴裂纹特征相符，因此可以判断转轴出现了裂纹。

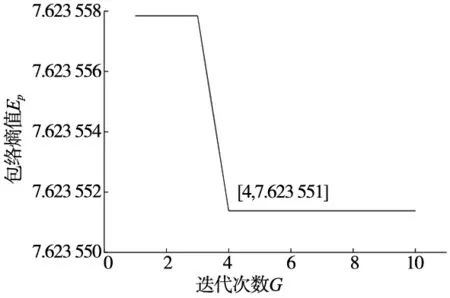
(a) VMD包络熵变化曲线

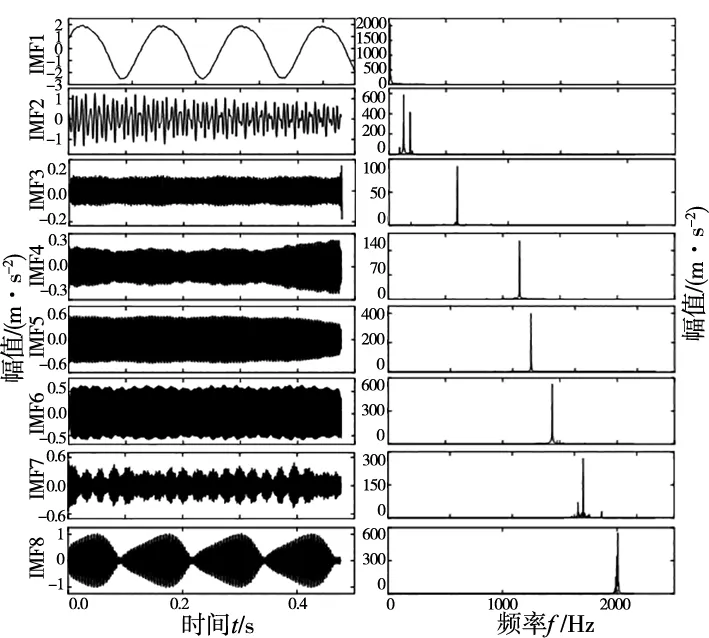
(b) 自适应VMD分解得到的模态分量及频谱

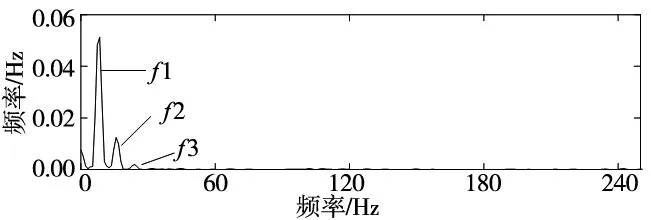
(c)自适应VMD最优分量包络谱

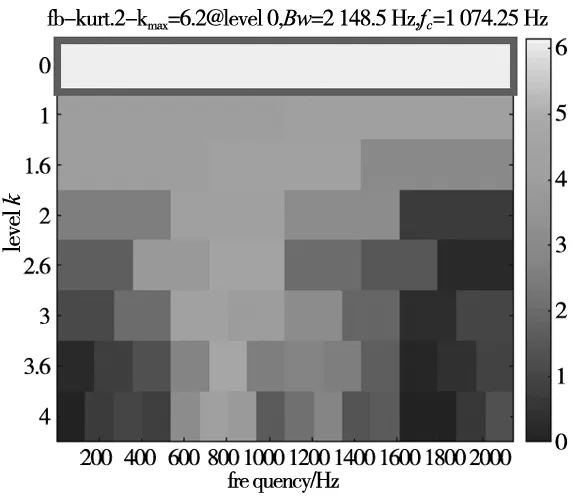
(d) 快速谱峭度图图3 自适应VMD+FSK处理仿真信号

作为对比，通过EMD算法对故障信号分析，同时利用相关系数法选择最优分量，得到最优模态函数及频谱，如图4a、图4b所示，并对最优分量进行滤波处理，如图4c所示。

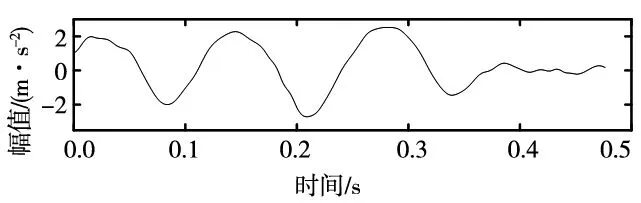
(a) EMD分解最优分量

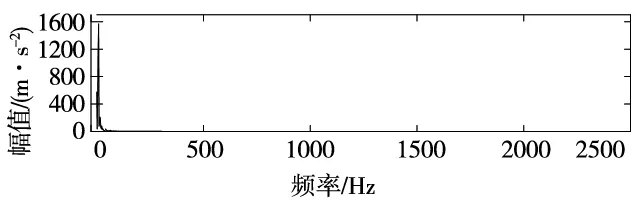
(b) EMD分解最优分量频谱

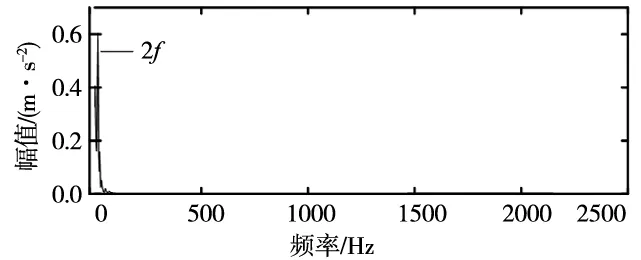
(c) 最优分量滤波处理图4 EMD+FSK最优分量包络谱

对比两种分解方法获得的最优分量包络谱可以看出，EMD+FSK只获得特征频率的2倍频，没有得到所有的故障信息，而通过PSO算法优化后的VMD+FSK可以最佳分量准确地提取出来，且包络谱中故障频率明显。故自适应VMD+FSK相对于EMD+FSK而言，获得的故障信息更加全面。

4 基于自适应VMD的转轴故障诊断

本文对转轴裂纹进行实验验证，试验采用Spectra Quest故障诊断综合实验台，试验台如图5所示。选用DEWESoft数据采集系统进行数据采集。主要的研究对象为含裂纹转轴传动系统，选取的故障转轴为输入轴，故障类型为转轴裂纹，转轴在传动的过程中出现故障时，故障振动信号会出现幅值和频率调制。本文中选取的故障类型为：采样频率为20 480 Hz、采样点数为3000点、输入转速为500 r/min。

图5 故障诊断综合试验平台

如图6所示为试验台采集的原始振动信号的时频域图，从时域图可以发现，当转轴发生故障时，出现频率调制，在时域图中呈现简谐波波形，同时也出现明显的噪声冲击信号，频谱中出现了其他的频率成分，无法判断转轴的故障类型。

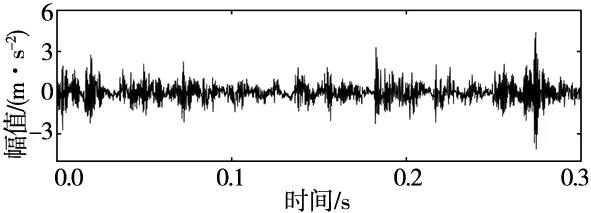
(a) 转轴含裂纹时域图

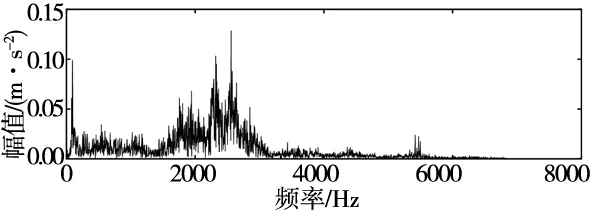
(b) 转轴含裂纹频谱图6 转轴含裂纹时频域

利用粒子群算法对VMD参数进行优化，通过自适应VMD对实验数据进行处理，如图7c所示，在第5代上出现局部极小包络熵7.427 5，局部极小包络熵所对应的最佳参数组合为[8，4472]，设置VMD分解最优参数对故障信号进行分解，利用相关系数法得到最优分量及其频谱，如图7a、图7b所示。利用快速谱峭度法对最优分量进行滤波处理。图7d所示为快速谱峭度图，从中可以得到最大峭度值为Kmax=5.1，出现层数levle=0，带宽为Bw=651.25 Hz，中心频率为fc=2 930.625 Hz。根据图中显示的参数，对最优分量进行带通滤波器设计。得到最佳分量包络谱如图7e所示。

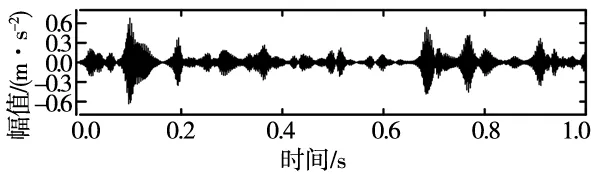
(a)VMD分解最优分量

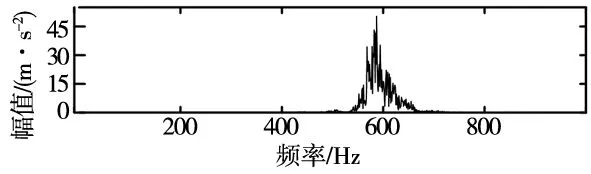
(b)VMD分解最优分量频谱

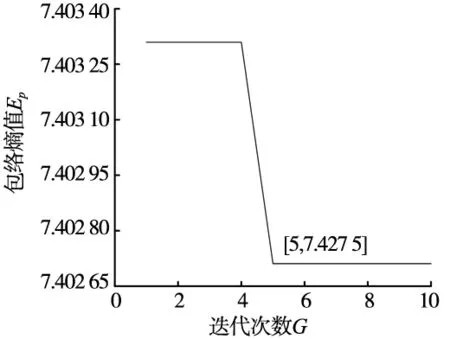
(c) VMD包络峰值因子变化曲线

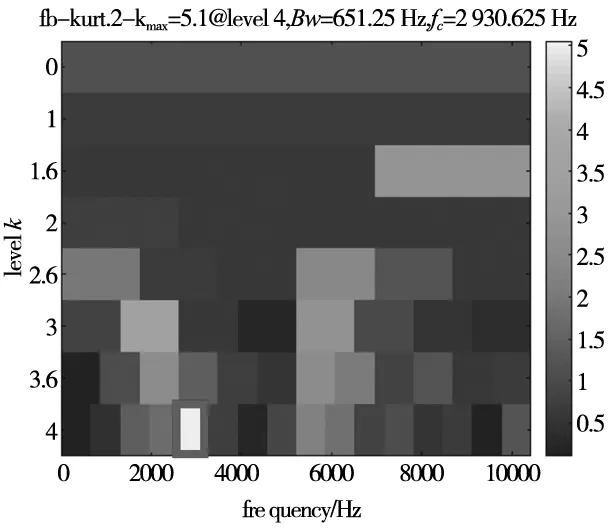
(d) 快速谱峭度图

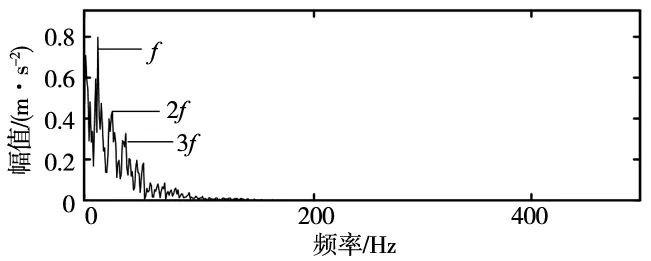
(e) VMD+FSK最佳模态分量包络谱图7 自适应VMD+FSK处理实验信号

运用同样的过程利用EMD+FSK对低速重载下转轴裂纹故障信号进行处理，如图8a、图8b所示为利用EMD分解后获得最佳分量及其频谱。如图8c所示为最佳分量的包络谱。

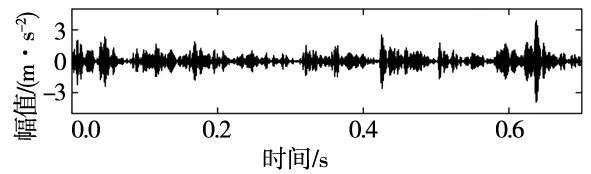
(a) EMD分解最优分量

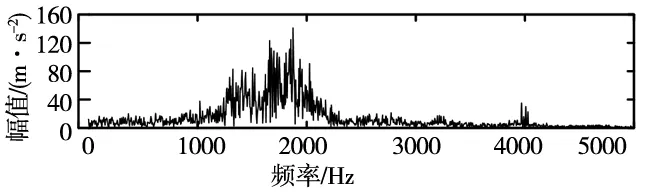
(b) EMD分解最优分量频谱

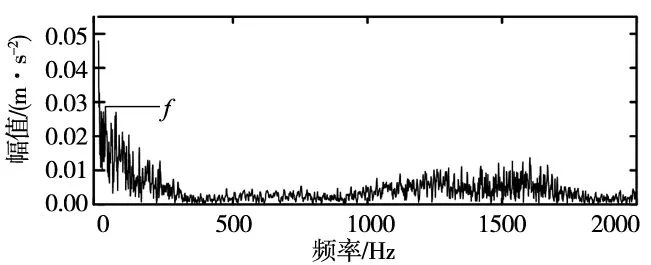
(c) EMD+FSK最佳模态分量包络谱图8 EMD+FSK处理实验信号

对比两种分解方法可以得到：对所提最优分量进行包络谱分析，其中不仅包含特征频率f，还含有其他频率成分，出现了频率混叠现象并且特征频率难以被发现；而利用PSO算法得到了VMD分解算法的最优组合参数，通过设置得到的组合参数可以准确地提取出最佳分量，且最优分量的包络谱中特征频率f及其2、3倍频成分清晰，噪声成分也得到了很好的抑制。综上分析可以看出，自适应VMD相对于EMD算法而言，可以准确分解故障信号并且得到全面的故障信息。

5 结论

针对转轴裂纹的故障特征难以提取的问题，本文使用基于自适应VMD结合快速谱峭度法的转轴裂纹的故障诊断方法，得出以下结论：

(1) 为避免VMD对信号分解时参数选取的盲目性，利用粒子群算法对VMD算法参数[K,α]进行优化，得到最优的参数组合。

(2) 通过相关系数法得到最优分量，结合快速谱峭度法对分量进行滤波处理，可以发现包络谱中的特征频率f及特征频率的2、3倍频幅值突出，与转轴的故障特征频率基本相符。通过该方法可以准确提取出故障信号的特征频率，因此可以判断转轴发生了故障。

(3) 仿真与实验结果表明，将自适应VMD 与快速谱峭度结合，能够有效地滤除噪声的干扰，准确地提取故障特征频率，与EMD结合快速谱峭度法对比，本文所提方法效果更好。