基于改进MF-DFA的零件特征提取与缺陷识别*

何 涛，王 幸，王少东，王正家，盛文婷

(湖北工业大学 a.机械工程学院；b.现代制造质量工程湖北省重点实验室，武汉 430068)

0 引言

零件作为工业制造领域中最基本的组成单元，其质量在工业制造领域中有着决定性的影响[1]。零件缺陷识别是实现产品质量检测的至关重要环节，保证产品质量对制造业的发展有着举足轻重的作用。由于在众多机械零件中诸如齿轮这类环形零件呈现非线性、不规则和一定自相似性的特点，使得传统检测工具很难准确识别零件缺陷。因此，探索一种有效的零件缺陷识别方法，以满足产品质量检测的需求。

分形理论作为一门新兴的非线性学科，适用于自然界中不规则事物的分析和处理。随着科学技术的发展，分形理论在图像处理中已取得广泛的应用和一系列的成果[2]。单分形方法仅用单一维数来描述目标物体的特征，不能完整地刻画其复杂性。文献[3]提出了多重分形理论，即利用广义维数与多重分形谱来描述客观物体。文献[4]在去趋势波动分析法(DFA)的基础上提出了多重分形去趋势波动分析(Multifractality Detrended Fluctuation Analysis,简称MF-DFA)，该方法避免了人为因素的影响，能够更准确地刻画隐藏在非平稳时间序列中的多重分形特征，可较大幅度提高目标物体的识别准确度[5]，目前该方法已经应用到各领域。文献[6]应用二维MF-DFA法计算糖尿病人的视网膜病变图像的局部广义Hurst指数，再将Hurst指数作为LSSVM中的训练输入量，对视网膜图像进行检测和分类识别，提高了图像识别的灵敏性和准确性。文献[7]引入滑动窗口技术对传统MF-DFA算法进行改进，计算液压泵的多重分形谱参数，最终利用半监督马氏距离模糊C均值法实现了液压泵退化状态的识别。

传统二维MF-DFA法存在过度覆盖的问题，因此本文提出一种基于改进MF-DFA的零件图像特征提取与缺陷识别研究方法。首先利用改进MF-DFA法计算预处理后的正常与缺陷齿轮图像的多重分形谱；然后选择多重分形谱中缺陷特征较为明显区域的数据，通过核化主成分分析法(Kernelized Principal Component Analysis，简称KPCA)从中获取齿轮图像的缺陷特征值；最后利用支持向量机(Support Vector Machines，简称SVM)实现齿轮缺陷识别。

1 多重分形去趋势波动分析

以多重分形算法为基础的多重分形去趋势波动分析算法得到了广泛应用，可用在二维以及高数位序列[8]。对于齿轮和轴承这类环形零件，需要使用二维多重分形去趋势波动分析(MF-DFA)法，能更全面刻画零件图像的信息，进而可以挖掘更显著的多分形特征。对MF-DFA法进行改进，提出三角覆盖的二维MF-DFA算法，可更精确地计算零件图像数据的多重分形谱，并高效地进行多重分形特征分析。

1.1 二维MF-DFA理论

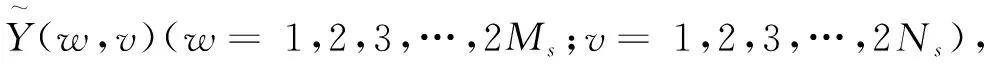
当q≠0时，测度波动函数Fq(s)为：

(1)

当q=0时，测度波动函数Fq(s)为：

(2)

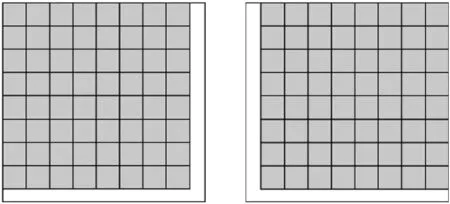
(a) 覆盖顺序1(b)覆盖顺序2

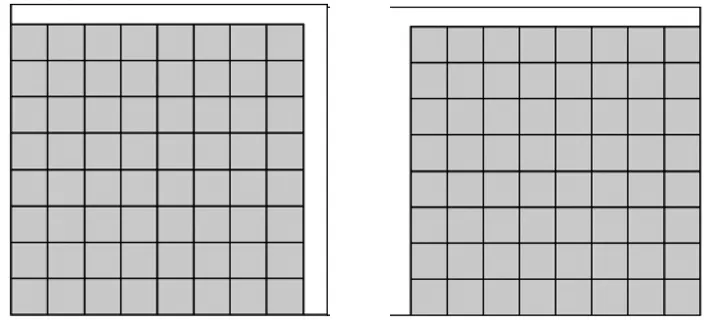
(c) 覆盖顺序3(d)覆盖顺序4图1 二维MF-DFA覆盖顺序

不断改变正方形模块的边长s，得到一组不同尺度s下的测度波动函数Fq(s)，再将log(s)和log(Fq(s))进行线性拟合运算得到广义Hurst指数h(q)，最后将其带入式(3)中计算奇异指数α与奇异谱f(α)，即可得到序列x(m,n)的多重分形谱。

(3)

1.2 三角覆盖的二维MF-DFA

在二维MF-DFA算法中，虽然使用正方形模块计算获得零件的多重分形谱较简便，但是该方法容易造成过度覆盖问题，导致计算结果不够准确。对比图2和图3可知，三角形模块覆盖图形轮廓曲线只计算不为零的模块部分，取得的覆盖轮廓比正方形模块覆盖轮廓更贴切地表达图像轮廓的本质。采用正方形模块覆盖轮廓曲线内的面积占整幅图像总面积的73.44%，而采用三角形模块覆盖相同轮廓曲线内的面积占图形总面积的61.33%。故可知三角形覆盖方法在保证图像完全覆盖的情况下，较好的解决了过度覆盖的问题，提高了图像覆盖的精确度。因此，本文引入三角形模块覆盖法替换传统正方形模块覆盖法，使用三角覆盖的二维MF-DFA分析目标图像的特征。

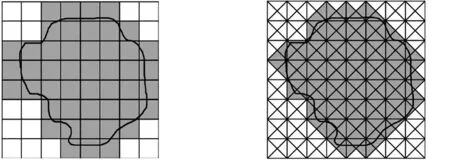
图2 正方形覆盖轮廓 曲线图像 图3 三角形覆盖轮廓 曲线图像

众所周知，二元多项式拟合运算的复杂度比一元一次多项式拟合运算的复杂度更高[9]。因此，本文的三角覆盖二维MF-DFA法选用一元一次多项式拟合来计算图像测度波动函数Fq(s)。具体流程如下所示：

(1)对一幅大小为M×N的图像x(m,n)构造去均值的和序列Y(i,j)。

(4)

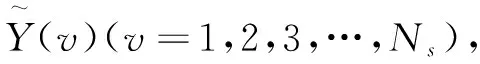
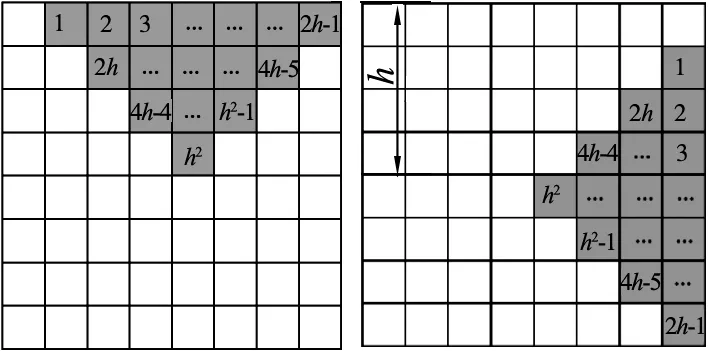
(a) 模块1 (b)模块2

(c) 模块3 (d)模块4图4 三角形覆盖模块

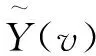
yv(k)=a1k+a2;k=1,2,...,s

(5)

(4)计算均方误差F2(s,v)

(6)

(5)对于Ns个小区间，求其F2(s,v)的均值，并计算q阶波动函数Fq(s)。

当q≠0时，测度波动函数Fq(s)为：

(7)

当q=0时，测度波动函数Fq(s)为：

(8)

(6)重复第(5)步，不断改变等腰三角形模块高h的数值，获得一组不同h值下的测度波动函数Fq(s)，对s和Fq(s)分别取对数得到log(s)和log(Fq(s))。将两者进行线性拟合得到广义Hurst指数h(q)，并带入式(3)中计算其对应的奇异指数α和奇异谱f(α)得到目标图像的多重分形谱。

2 齿轮图像特征值提取

2.1 齿轮多重分形特性分析

如果直接对系统采集的图像进行广义Hurst指数h(q)计算，图像的背景区域和噪音光斑会对最终的计算结果造成影响。故在计算广义Hurst指数h(q)前需对图像进行预处理，即将采集的齿轮图像经过二值化、面积滤波、背景区域灰度值还原以及零件区域灰度值取反处理后，零件图像区域的特征被完整保留，如图5所示。

(a) 正常齿轮预处理图像 (b)缺齿齿轮预处理图像图5 齿轮零件预处理图像

齿轮这类零件的图像具备分形特性，判断这类零件图像是否满足多重分形的特征，需要计算这类零件图像的广义Hurst指数h(q)，当对应的h(q)值随着q的变化而变化时，齿轮零件图像才具有多重分形特性。使用三角覆盖二维MF-DFA算法对经过预处理后的齿轮图像进行分析和计算得到其广义Hurst指数h(q)，其中q值范围为-13.5～+13.5，取值间隔为0.1。计算结果如图6所示，其中q值为横坐标，广义Hurst指数h(q)值为纵坐标，可以观察到正常与缺陷齿轮图像的h(q)均随着q值的改变而显著变化。据此可知正常与缺陷齿轮图像具有多重分形特性，并用多重分形谱对其进行特征分析。

图6 正常与缺陷齿轮零件预处理图像Hurst指数h(q)

2.2 齿轮图像多重分形谱计算及其缺陷分析

使用三角覆盖的二维MF-DFA算法分别对正常与缺陷齿轮图像进行多重分形谱的计算，计算结果如图7所示，图中横坐标为奇异指数α，纵坐标为对应的奇异谱f(α)。

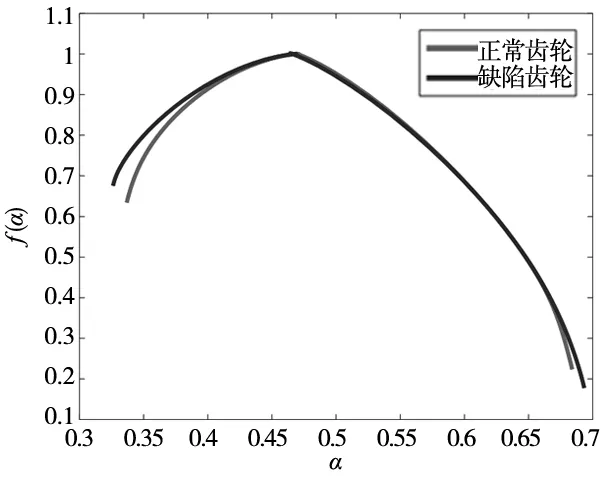
图7 正常与缺陷齿轮图像的多重分形谱

单张齿轮图像的多重分形谱不能充分诠释齿轮零件图像的整体特征。为了得到齿轮零件最具代表性的特征值，采集正常与缺陷齿轮在不同位置状态下的图像各20张，分别计算这些图像的多重分形谱，将计算好的20张正常齿轮零件图像的多重分形谱与其对应的20张缺陷齿轮的多重分形谱以不同颜色绘制在图8中，用于齿轮图像的缺陷特征分析。

从图8可知，多重分形谱线顶点(奇异谱f(α)为最大值的点)的右侧，正常齿轮图像多重分形谱线与缺陷齿轮图像的多重分形谱线相互杂糅，区分困难。而在谱线顶点的左侧，正常齿轮图像与缺陷齿轮图像的多重分形谱线相互错开，各自成束，缺陷特征明显，易于区分。故选择多重分形谱线顶点左侧区域的数据作为齿轮缺陷特征数据资源，如图9所示，图中每条谱线分别代表其对应的齿轮零件图像的特征数据。

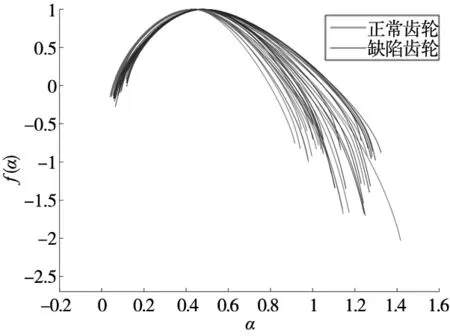
图8 齿轮图像多重分形谱

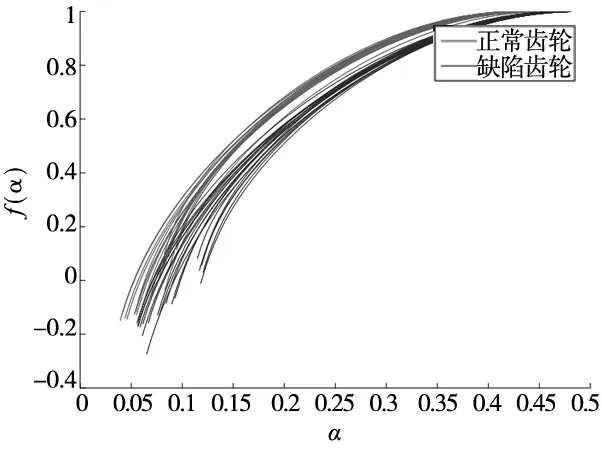
图9 齿轮缺陷特征数据资源

2.3 齿轮图像多重分形谱缺陷特征值提取

齿轮缺陷特征数据资源来自20张正常齿轮图像与20张缺陷齿轮图像，每张图像包含106个数据，即每张齿轮图像包含106个特征值，特征值维数为106。核主成分分析(KPCA)作为主成分分析(PCA)的一种非线性扩展方法[10]，KPCA是在PCA的基础上利用非线性映射函数完成非线性变换，将非线性的原始低维空间数据映射到高维线性特征空间中，在线性特征空间中利用PCA算法对数据进行特征提取，从而有效地提取样本数据的非线性信息[11]。故本文选用核主成分分析(KPCA)算法对这些数据进行降维处理，获得精确的齿轮图像缺陷特征值。

KPCA算法具体降维步骤如下所示：

(1)选取样本个数为n，影响因子为m，构成的样本数据集为A：

(2)选用核函数，目前常用的核函数主要有多项式核函数、神经网络核函数以及高斯径向基(RBF)核函数[12]。其中径向核函数计算过程较简便且分类效果好，其表达式：

(9)

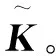
(10)

其中，

(5)选择较大特征值的主成分，即选取前q个λi的累计贡献率Bq需大于值0.95，如式(11)所示：

(11)

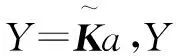
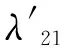
图10 A特征值的累计贡献率Bi

将每张正常与缺陷齿轮图像的特征值作为二维空间点的位置坐标，如图11所示。观察此图可知，齿轮缺陷数据点组成了两个群簇分别代表正常和缺陷齿轮零件图像，表明齿轮缺陷特征提取成功。

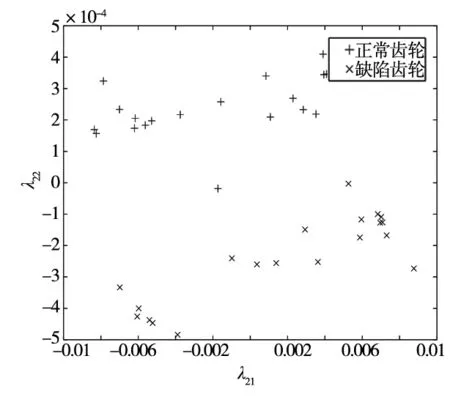
图11 齿轮图像缺陷特征值

3 基于MF-DFA和Lib-SVM的齿轮缺陷识别

3.1 齿轮图像缺陷识别数据准备

(1)获取齿轮图像缺陷识别训练集与测试集

成功提取齿轮图像的缺陷特征值Y，Y为40×2的矩阵，由20张正常齿轮图像和20张缺陷齿轮图像组成，矩阵Y的每行数据代表每张齿轮图像的缺陷特征值。将Y转化为齿轮图像缺陷识别的训练集与测试集，根据Lib-SVM的标准[13]进行格式调整。

随机抽取Y中10张正常和10张缺陷齿轮图像的缺陷特征值，将其整合后作为齿轮缺陷训练数据集D2。整合剩余的10张正常与10张缺陷齿轮图像的特征值作为齿轮图像缺陷测试数据集E2。D2与E2均是大小为20×2的矩阵。根据Lib-SVM标准调整D2与E2的格式，对它们进行归一化处理得到齿轮图像的缺陷标准训练集train_chq2和测试集test_chq2。train_chq2与test_chq2皆是大小为20×2的矩阵。D2、E2、train_chq2及test_chq2的数据量较大，本文将每张齿轮图像的缺陷特征值作为每个二维空间点的位置坐标，如图12和图13所示，即D2、E2、train_chq2及test_chq2用二维图像进行表达。

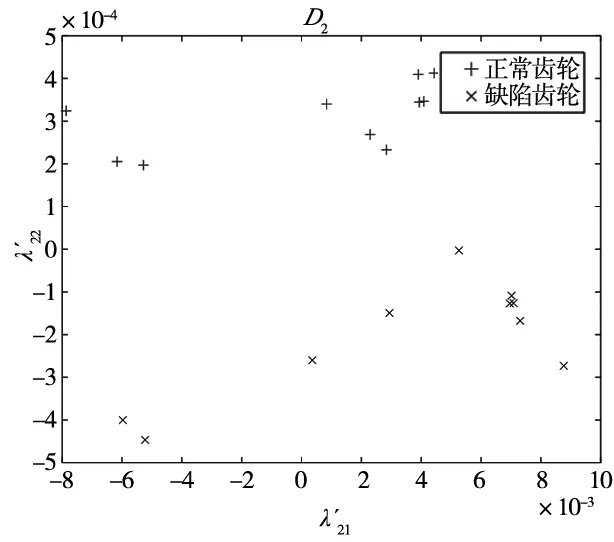
(a) 齿轮图像缺陷训练数据集D2

(b) 齿轮图像缺陷测试数据集E2图12 齿轮图像缺陷训练与测试数据集

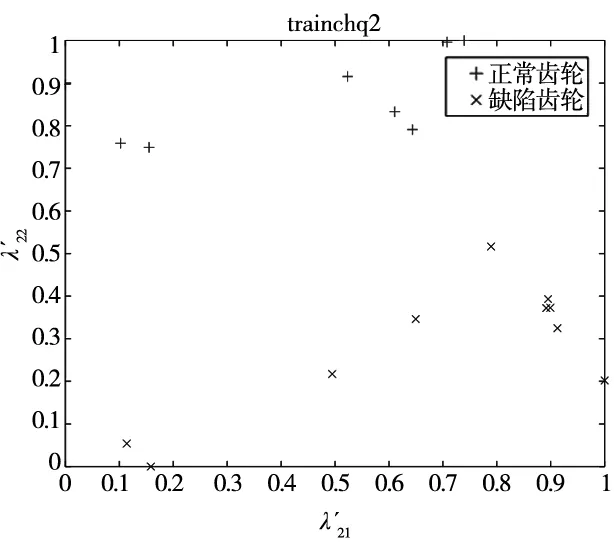
(a) 齿轮图像缺陷标准训练集train_chq2

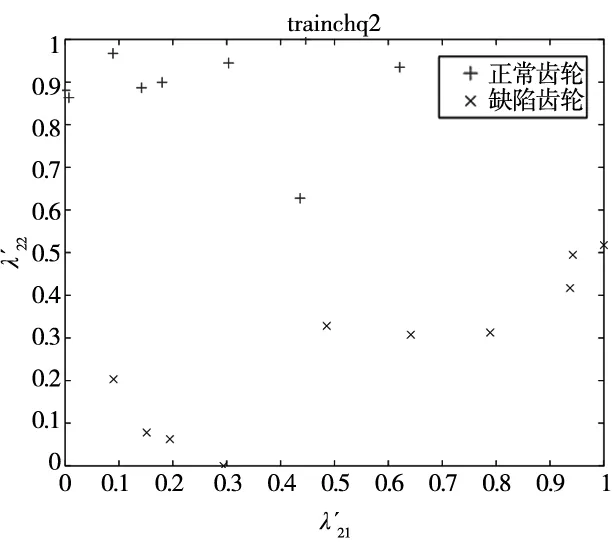
(b) 齿轮图像缺陷标准测试集test_chq2图13 齿轮图像缺陷标准训练集与测试集

(2)齿轮图像缺陷识别Lib-SVM最佳参数选择

得到齿轮图像的缺陷标准训练集train_chq2后，需要将其进行交叉验证以获取Lib-SVM齿轮图像缺陷识别的最佳惩罚因子c2和核函数参数g2。

在范围2-7～27内多次改变(c2,g2)的数值，将train_chq2中20张图像的数据随机分成4个数据量相同的部分，依次将train_chq2的每一个部分作为齿轮测试集进行预测，train_chq2其他3个部分作为齿轮图像训练集对Lib-SVM进行训练，分别计算这四个部分齿轮缺陷识别准确率的平均数p，取使p值最大时其对应的惩罚因子c2和核函数参数g2作为齿轮缺陷识别的最佳参数。

交叉验证结果如图14所示，图中的线条为p等高线，每条线上的数值为p的100倍。本次测试p的最大值为100%。且有多组的数值不同的(c2,g2)参数组合可以使得p取得最大值。当惩罚参数c2过高时会造成过学习状态，因此选取其中惩罚参数c2最小的那组作为最佳参数值，故本次最佳参数(c2,g2)的取值分别为c2=0.007 812 5，g2=0.007 812 5。

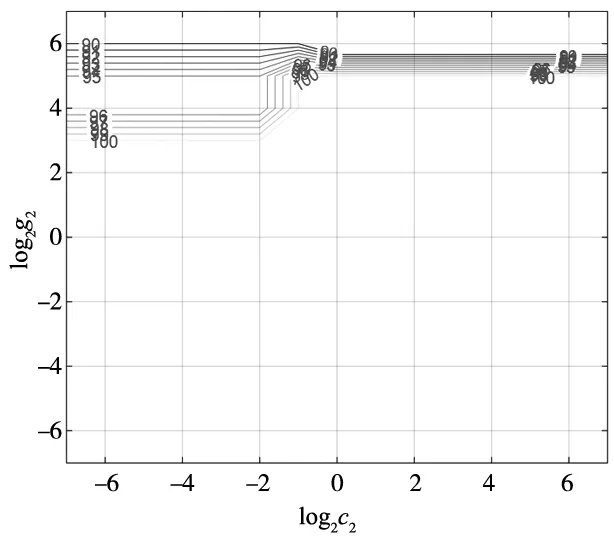
图14 最佳参数(c2,g2)交叉验证结果

3.2 齿轮缺陷识别预测结果与数据分析

(1)齿轮缺陷识别预测结果

将齿轮图像最佳缺陷识别参数(c2,g2)与训练集train_chq2带入Lib-SVM中的样本训练函数(svmtrain)进行训练可获得齿轮图像缺陷识别SVM模型model。随后将model和测试集test_chq2带入Lib-SVM中的模型测试函数(svmpredict)进行分类运算即可获得齿轮图像缺陷识别预测结果。本次齿轮图像缺陷识别预测准确率Accuracy1为100%，标志着本次齿轮图像缺陷识别成功。

如图15所示，测试集test_chq2中20张正常与缺陷齿轮图像的特征值全部被精准识别预测，用不同形状和不同颜色的几何图形标示。其中上部区域代表正常齿轮图像特征值预测结果，下部区域代表缺陷齿轮图像特征值预测结果。

图15 齿轮图像缺陷识别预测结果

(2)齿轮缺陷识别结果分析

本次研究的齿轮图像缺陷识别预测结果准确率高达100%，结果分析如下：一方面根据齿轮图像缺陷特征数据资源，正常齿轮图像与缺陷齿轮图像的多重分形谱线各自聚集成束，大致错开且无重叠现象，谱线的缺陷特征明显。验证了本文提出的基于三角覆盖二维MF-DFA法计算的多重分形谱可以很好地表达零件图像的缺陷特征。根据齿轮图像缺陷特征值数据，进一步得到正常与缺陷齿轮图像的数据点各自聚集成簇，同时证明本次选用KPCA可以精确提取零件图像的缺陷特征值，再利用Lib-SVM算法建立零件图像缺陷识别模型，能够对零件的缺陷状态进行精准识别预测。

4 总结

本文将常用的多重分形去趋势波动进行改进，提出了一种基于三角覆盖的二维MF-DFA算法，用来表达齿轮图像的缺陷特征。使用KPCA法融合多重分形和核主成分分析，提取齿轮图像的多重分形缺陷特征值，再采用Lib-SVM对齿轮图像数据进行建模和缺陷识别，识别准确率高达100%。结果表明运用该方法可以很好地识别零件图像的缺陷，标志着零件图像缺陷识别成功，同时验证了三角覆盖二维MF-DFA法能够较好地表达零件的缺陷特征。