低张力下纬平针织物线圈结构拉伸变形

吕常亮，陈慧敏，岳晓丽

(东华大学 机械工程学院，上海 201620)

针织物是由线圈单元相互嵌套而成的织物[1]，不同于机织物的经纬纱交织结构，针织结构具有更加明显的张力敏感性。在针织物平幅印染加工中，过大的张力会导致针织物线圈过度变形，进而造成针织物染色不匀、丝光柔软度差、卷形不佳等缺陷[2]。因此针织物平幅加工中通常要求张力低于30 N[3]。纬平针织物在低张力下的宏观拉伸变形是线圈细观结构变形的结果，并且低张力拉伸状态下的线圈滑移是影响织物变形的主要因素，因此，准确计算针织物的拉伸变形是针织物平幅印染过程中低张力控制的关键。

针对针织物拉伸变形问题，国内外学者展开了一系列研究。Hearle等[4]研究表明，针织结构内部储存弯曲能量，在松弛状态下存在一个最小能量状态。随后，根据能量守恒定律研究针织物线圈变形的方法逐渐受到学者的关注。Choi等[5]研究表明，拉伸状态下针织物的线圈结构参数随载荷的变化规律近似满足余弦函数关系式，当线圈单元数低于10个/cm时，织物宏观拉伸变形是由纱线弹性弯曲所导致的线圈结构变化。Karimi等[6]基于卡氏定理并考虑纱线的可压缩性、抗弯性等因素，对针织物初始弹性模量进行了预测。上述研究证实了针织物在松弛状态下具有初始能量的结论。而在研究拉伸状态下针织物变形过程中线圈结构变化与拉伸载荷及纱线参数之间的关系时，Popper[7]研究发现，当针织物的线圈圈高收缩变形不小于4倍纱线直径、圈距收缩变形不小于8倍纱线直径时，纱线间的摩擦损耗会对针织物的拉伸变形产生影响。Hong等[8]在Popper的模型基础上建立了线圈特征点坐标与线圈结构参数及纱线性能参数之间的关系模型，提出可应用于单轴、双轴拉伸作用下的针织物线圈变形计算方法。Dusserre[9]同样基于Popper的模型，分析不同种类纱线间的滑动摩擦对针织物拉伸过程能量损耗的影响，并指出针织物拉伸具有滞后性的特点。

本文在Hong等[8]建立的模型基础上，以纬平针织物为研究对象，通过建立线圈细观结构下的几何模型及力学模型，探究线圈结构参数、纱线力学性能参数与拉伸载荷之间的关系。重点讨论低张力作用下线圈构型对摩擦角的影响，从而探究纱线滑动摩擦对宏观织物拉伸变形的影响，并将该模型应用于织物沿幅宽方向上线圈变形的不均匀计算。研究旨在为针织物平幅印染加工中不同规格织物的张力控制设定提供参考，并对纬平针织物宏观拉伸过程中的载荷-应变关系和线圈细观结构变化进行预测分析。

1 线圈结构拉伸变形模型构建

1.1 假设条件

纬平针织物的线圈结构具有如图1所示的周期性排布特点，取图示线圈单元的1/4作为研究对象[8]，其几何形状和受力状态如图2所示。对该1/4线圈模型作出以下假设：(1)纱线不可伸长；(2)纱线为均质弹性杆；(3)相邻线圈之间相互嵌套且相互接触，相邻线圈接触点之间的距离等于纱线直径；(4)相邻线圈间的接触力可等效为接触点处的支反力。

图1 针织物线圈周期性结构示意图Fig.1 Schematic of periodic structure of knitted fabric loop

图2 1/4线圈模型示意图Fig.2 Schematic of quarter loop model

1.2 几何模型

由图2可知，B点为相邻线圈的接触点，XB、YB为接触点B在xOy坐标系下的横、纵坐标，β为弧AC在点B处切线与x轴正方向之间的夹角，α为弧AC在点A处切线与x轴正方向之间的夹角。根据几何模型特征点的位置关系，建立线圈结构参数与特征角度及接触点B之间的关系，如式(1)所示。

(1)

式中：C、W分别为圈高、圈距；L为线圈单元总弧长；d为纱线直径；SAB、SBC分别为弧AB和BC的弧长。

1.3 力学模型

由图2可知：拉力P、T分别为线圈单元沿纵行和横列方向所受的作用力；力矩M为织物厚度方向的弯曲力矩；角γ为P作用方向与x轴负方向之间的夹角；y′AB为B点到P作用方向之间的垂直距离；yBC为B点到T作用方向之间的垂直距离。

在拉伸过程中，线圈接触点B在弧段上的位置将发生改变。考虑到纱线滑移对拉伸变形的影响，引入作用于支反力R处的线圈摩擦角φ，φ由支反力R的切向分量Rt与法向分量Rn的比值来确定，如式(2)所示。

(2)

式中：μ为等效摩擦因数；μk为纱线滑动摩擦因数；θ为图3所示相邻线圈间的缠绕角度。图3中心处圆的直径等于纱线直径。

图3 线圈间缠绕角度示意图Fig.3 Schematic of winding angle between loops

根据线圈受力平衡条件建立拉力T和支反力R的表达式如式(3)和(4)所示。

(3)

(4)

接触点B将1/4线圈模型分割成AB、BC两弧段，通过对弧段AB、BC进行分析以获取弧长表达式及接触点B的坐标方程。

1.3.1 弧段AB

弧段AB的受力情况如图4所示。将原坐标系原点平移至A点，并逆时针旋转角度γ得到x′O′y′坐标系。

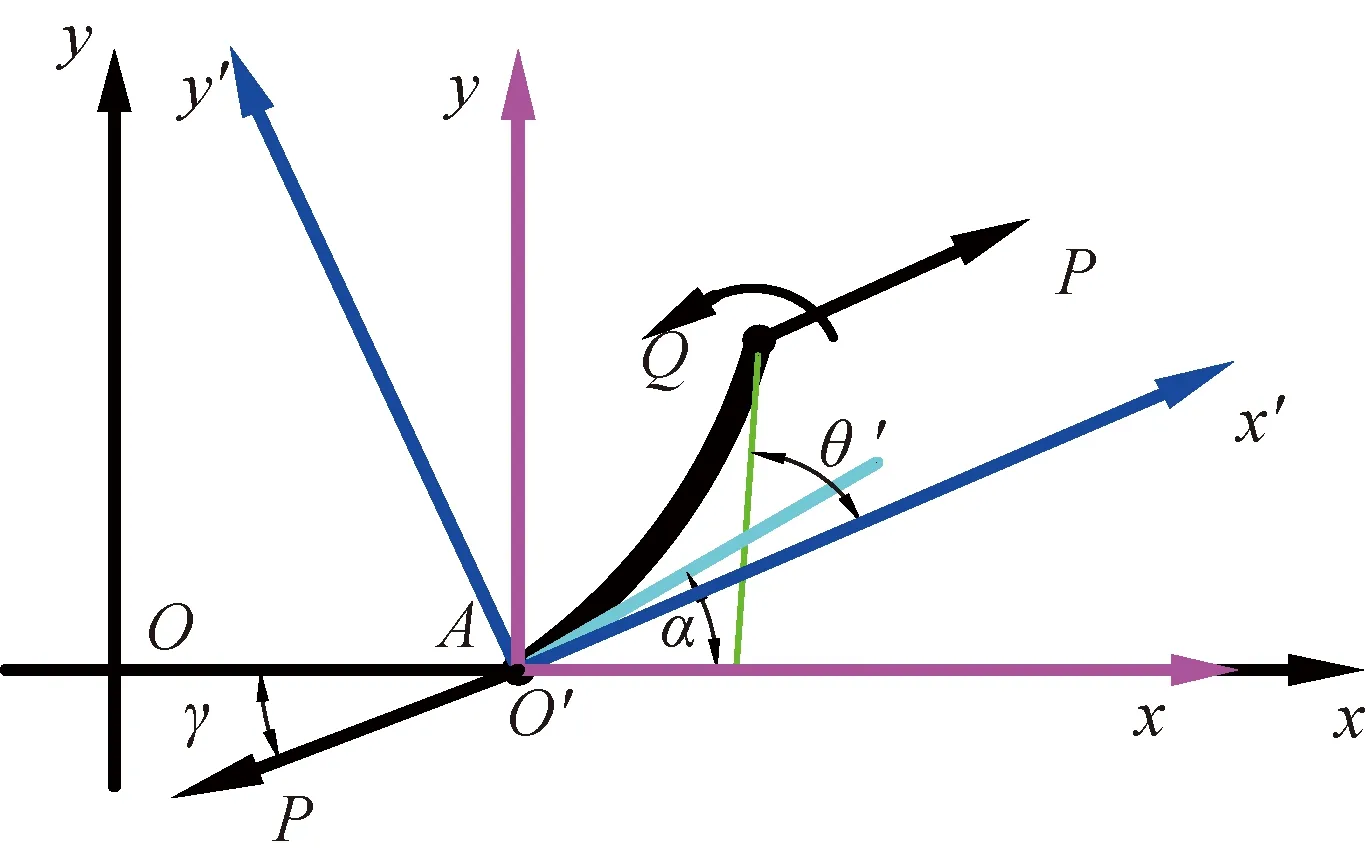
图4 弧段AB受力图Fig.4 Force analysis of arc AB

在坐标系x′O′y′中，弧段AB上任意一点Q(x′,y′)，对A点求弯矩平衡，得到夹角θ′关于抗弯刚度B和作用力P的微分方程如式(5)所示。

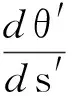
(5)

式中：B为纱线的抗弯刚度；s′为线圈单元弧长。求解微分方程得到接触点B的坐标(x′B,y′B)及线圈弧长SAB表达式如式(6)～(8)所示。

(6)

(7)

(8)

式中：

(9)

(10)

f(ε1,φ1B)=F(ε1, π/2)-F(ε1,φ1B)

(11)

e(ε1,φ1B)=E(ε1, π/2)-E(ε1,φ1B)

(12)

式中：F(ε1, π/2)、F(ε1,φ1B)分别为第一类完全椭圆积分和不完全椭圆积分；E(ε1, π/2)、E(ε1,φ1B)分别为第二类完全椭圆积分和不完全椭圆积分。

1.3.2 弧段BC

弧段BC的受力情况如图5所示，其任意一点Q(x,y)受到与点C处大小相等、方向相反的作用力。

图5 弧段BC受力图Fig.5 Force analysis of arc BC

对C点求弯矩平衡，得到夹角θ关于抗弯刚度B和作用力T、力矩M的微分方程如式(13)所示。

(13)

将微分方程代入方程(6)～(8)消去拉力T、力矩M得到弧长BC的表达式如式(14)所示。

(14)

式中：

(15)

k1=cosγ+sinγtan(β+φ)

(16)

(17)

(18)

根据上述弧段AB、BC的受力分析结果，可得到接触点B坐标及弧长表达式。

1.4 简化方程

将方程(4)、(6)、(7)、(14)代入方程(1)，消去拉力P和抗弯刚度B，得到描述线圈结构参数与空间角度之间的简化方程如式(19)～(21)所示。

(19)

(20)

(21)

式中：L、W、C、d分别为线圈单元的弧长、圈距、圈高、纱线直径，简化方程中的中间变量c1、c2、c3、c4的表达式如式(22)～(25)所示。

(22)

c2=[f(ε1,φ1B)-2e(ε1,φ1B)]sinγ+
2ε1cosφ1Bcosγ

(23)

c3=[f(ε1,φ1B)-2e(ε1,φ1B)]cosγ+
2ε1cosφ1Bsinγ

(24)

(25)

式中：k2、ε2、φ2B、ε1、φ1B分别由式(15)、(17)、(18)、(9)、(10)计算得到；f、e分别由式(11)和(12)计算得到。

根据上述简化公式，重新计算表达式(3)和(4)，得到变化后的纵向拉力P、横向拉力T的表达式如式(26)和(27)所示。

(26)

T=-k1P

(27)

式中：B为纱线的抗弯刚度；c4为简化方程的中间变量，由式(25)计算得到；L为线圈单元的弧长；k1由式(16)计算得到。根据上述分析方程建立线圈结构参数与特征角度及拉伸载荷之间的关系式。

2 纱线抗弯刚度及线圈结构参数测定

2.1 纱线抗弯刚度

纱线抗弯刚度采用KES-FB2型弯曲测试仪测定，纱线规格为14.6、18.2、22.4 tex纯棉纱线，制作如图6所示的待测试样，试样粘贴40根纱线且保持相互平行、松紧一致。

图6 纱线抗弯刚度待测试样示意图Fig.6 Schematic of test sample for yarn’s bending stiffness

纱线测试试验在恒温恒湿实验室进行，测得14.6、18.2、22.4 tex纱线的抗弯刚度分别为5.98×10-3、6.20×10-3和3.20×10-3cN·cm2。

2.2 纬平针织物结构参数

由于纬平针织结构本身存在不均匀性及结构尺寸较小的特点，手动测量结果的准确性不高，采用图像处理技术和统计学方法确定针织物的结构参数，以减小测量误差从而提高准确性。采用VHX-2000型超景深显微镜分别拍摄14.6、18.2、22.4 tex纯棉纱织物线圈结构照片，经滤波、灰度化、灰度均衡化[10]处理得到的线圈结构灰度图像如图7所示。

(a) 14.6 tex

处理后图像转换成为1 600像素×1 200像素的灰度矩阵，根据线圈结构的周期性灰度变化特点，计算得到3种针织物的结构参数, 如表1所示。

表1 线圈结构参数

3 计算实例

3.1 纬平针织物拉伸变形计算流程

根据测得的3种纬平针织物的初始结构参数圈距W0、圈高C0和单元弧长L0求解方程(19)～(21)，解得的初始角α0、β0、γ0及初始拉力P0、T0如表2所示。

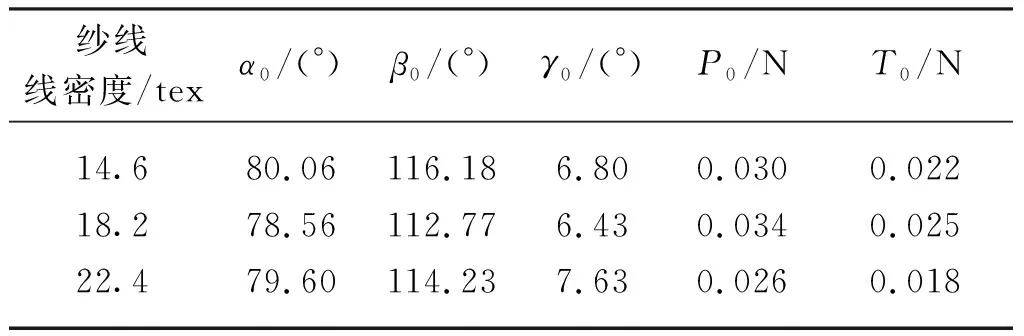
表2 线圈初始状态参数值

在已知初始角α0、β0、γ0及初始拉力P0、T0后，对纬平针织物沿纵行和横列方向上的拉伸载荷-应变进行迭代计算。此时将纱线抗弯刚度B、纱线直径d作为输入参数，结构参数W0、C0、L0为已知参数，按一定步长大小增大纵行和横列拉伸应变εC、εW，求解纵行和横列方向的拉伸载荷FTC、FTW。当织物沿纵行方向拉伸时，线圈结构参数C逐渐增大。假设上述初始拉力T0及线圈单元弧长L0保持不变，以ΔC=1 mm步长进行迭代。沿横列方向拉伸时，线圈单元结构参数W逐渐增大，此时假设弧长SBC保持不变，以ΔW=1 mm步长进行迭代计算。具体拉伸计算流程如图8所示。

图8 拉伸计算流程Fig.8 Stretch calculation process

针织物拉伸试验采用HZ-1007E型拉压仪，测试条件参照FZ/T 70006—2004《针织物拉伸弹性回复试验方法》，试样规格为130 mm×50 mm，预留30 mm夹持长度，实际有效尺寸为100 mm×50 mm，拉伸速率为30 mm/min。

3.2 滑动摩擦对拉伸载荷计算结果的影响

计算得到的3种纬平针织物的载荷-应变计算结果如图9所示。

图9 模型计算结果(φ=0)Fig.9 Calculation results (φ=0)

由图9可知，若在计算模型中不考虑纱线的滑动摩擦，3种织物的拉伸载荷计算值均小于试验值。这是由于模型中的载荷计算忽略了线圈间滑动摩擦产生的阻尼力，因此针对纱线间滑动摩擦对纬平针织物拉伸变形的影响进行讨论。以14.6 tex针织物为例，根据图3所示模型测得最小摩擦角θmin=48°，根据式(28)估算得到最大摩擦角θmax=117°。

(28)

由于θ的最大值是根据模型化方程得到的，直接采用该值计算拉伸载荷往往会产生较大的误差，因此计算并给出θ在40°～120°、40°～100°、60°～120°内随迭代步长变化的拉伸载荷-应变曲线。纯棉纱线的滑动摩擦因数[11]μ取0.453，载荷-应变计算结果如图10所示。

图10 滑动摩擦角对载荷计算影响Fig.10 Effect of friction angle on load calculation

由图10可知，当摩擦角θ在40°～120°内变化时，模型能够较好地描述纬平针织物沿纵行方向的拉伸载荷应变状态，具有较好的计算精度。

3.3 沿纵行和横列方向的拉伸载荷与应变

根据上述摩擦角的讨论，计算并给出3种纬平针织物沿纵行方向和横列方向拉伸载荷-应变曲线，如图11所示。

(a) 沿纵行方向

(b) 沿横列方向

由图11可知，线圈纵行和横列方向的载荷与应变的计算值和试验值均吻合较好，其中14.6 tex纬平针织物沿横列方向的计算相对误差最大为9.8%。 在0.1应变下，纵行方向的拉伸载荷大于横列方向，14.6、18.2 tex纬平针织物纵行方向的拉伸载荷分别为0.609、0.862 N，横列方向的拉伸载荷分别为0.372、0.462 N，其中纵行方向的拉伸载荷约为横列方向的1.7倍，而22.4 tex针织物纵行和横列方向的拉伸载荷分别为0.468、0.388 N，纵行方向的拉伸载荷约为横列方向的1.3倍。由此可见纬平针织物纵行与横列方向的力学性能差异较大。

3.4 沿幅宽方向的线圈不均匀变形

纬平针织物在拉伸过程中垂直于拉伸方向上的纱线由于泊松效应会发生收缩，与传统固体材料不同，针织物的收缩是线圈结构参数缩小的宏观表现。纬平针织物在拉伸初始阶段，沿幅宽方向由于线圈结构不均匀导致构型角度存在差异，因此考虑在从幅宽中心处到两边的迭代计算中通过逐渐减小线圈构型的初始角度值来模拟线圈沿幅宽方向变形的不均匀性。使用工业相机拍摄如图12所示的针织物试样上5个标记点处变形后的线圈结构，拉伸测试条件与3.1节中的条件相同，计算结果与试验结果如图13所示。

图12 针织物标记试样Fig.12 Knitted fabric marking sample

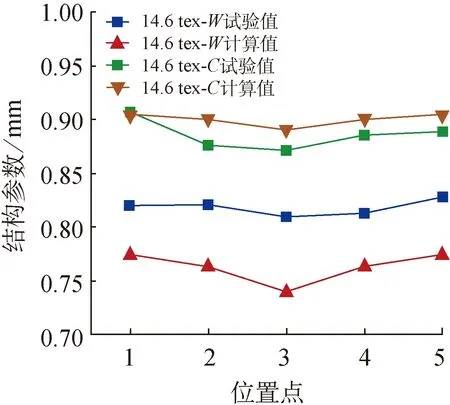
(a) 14.6 tex

由图13可知，对于40S、32S、26S的3种针织物，计算结果中最大变形位置处的圈距W分别为0.738、0.674、0.468 mm，最大变形位置处的圈高C分别为0.868、0.819、0.640 mm。通过测量5个位置点处的线圈结构参数，求解不同的初始角度值代入拉伸载荷-应变的迭代计算。由图13可知，计算所得曲线呈中心处变形大、两端变形小的趋势。在幅宽方向上5个位置点处计算值与试验值的最大相对误差如表3所示，其中最大相对误差为位置点3的计算值与试验值的差值与试验值的百分比值。

表3 不均匀变形计算的最大相对误差

由图13和表3可知，考虑纱线滑动摩擦下的拉伸计算模型可以有效模拟织物沿幅宽方向的不均匀变形，拉伸后线圈结构参数沿幅宽方向上的收缩变形计算结果呈出中心处变形较大而两端变形较小的趋势。14.6 tex织物的计算结果与试验测量值之间的相对误差较大，其中圈距W的最大相对误差为-9.20%， 这是由于14.6 tex织物结构较为疏松，拉伸过程中纱线间发生较大的滑动而自身结构参数变化较小，但拉伸载荷-应变的计算相对误差绝对值均在9.8%以内。

4 结 语

研究低张力作用下纬平针织物沿纵行和横列方向的拉伸载荷变形问题，建立考虑摩擦效应的纬平针织物的几何、力学模型，通过图像处理及统计学方法得到3种纬平针织物的初始结构参数，讨论拉伸过程中滑动摩擦角变化对模型计算精度的影响，并将模型用于沿幅宽方向上的收缩变形计算，得出如下结论：

(1)摩擦角θ在40°～120°内变化时能够有效提高模型的计算精度，模型能够较好地表达织物拉伸状态下的载荷-应变状态，相对误差总体控制在9.8%以内。

(2)纬平针织物在低张力作用下沿纵行和横列方向的力学性能存在较大差异，14.6、18.2 tex织物沿纵行方向的拉伸载荷约为横列方向的1.7倍，而22.4 tex织物约为1.3倍。

(3)模型能够计算沿幅宽方向的线圈结构不均匀变形，且纬平针织物拉伸后呈中心处变形较大、两端变形较小的特点。