二阶非完整平面欠驱动机械系统的位置控制

黄自鑫，秦翔宇，王乐君

1. 武汉工程大学电气信息学院，湖北 武汉430205；2. 中国地质大学（武汉）自动化学院，湖北 武汉430074

非完整系统是指一类具有非完整约束的非线性系统［1］，非完整约束可分为一阶非完整系统和二阶非完整系统［2］。欠驱动连杆机械系统是一类驱动关节个数少于系统自由度个数的非线性系统［3-4］，即系统的控制输入维数少于系统位形空间的维数［5］。其中，主要研究对象为垂直欠驱动连杆系统（含重力）［6］和平面欠驱动连杆系统（不含重力）［7-8］。近年来，国内外学者针对垂直欠驱动机械系统进行了广泛的研究。与垂直欠驱动系统相比，平面欠驱动机械系统的任意可达位置均为系统的平衡点，且该类系统的近似模型不满足线性可控条件［9］，无法采用垂直欠驱动系统的控制方法实现其稳定控制。

其中，针对平面三连杆欠驱动机械系统，主要依据欠驱动关节的位置进行分类研究。首关节为欠驱动的平面三连杆系统是一阶非完整系统，文献［10］提出一种基于模型降阶的位置控制方法，将原系统分段降阶为两个平面虚拟Acrobot 系统，并依据平面Acrobot 系统的角度约束关系进行有效控制。末关节为欠驱动的平面三连杆系统是二阶非完整系统，文献［11］将系统转换为链式规范型，设计控制器进行控制。而对中间关节为欠驱动的平面三连杆系统，文献［12］提出一种末端滑模控制的方法，当欠驱动关节的速度小于设置阈值时被锁住，将系统控制到目标位置，该方法使被控对象不再具有欠驱动特性。基于上述分析，针对中间关节为欠驱动的平面三连杆系统的位置控制是一个开放的问题。

本文针对中间关节为欠驱动的平面三连杆系统（简称平面APA系统），提出一种模型降阶的分段控制策略，实现系统位置控制目标。首先，控制第一连杆到达目标位置，并控制第三连杆角度和角速度为零，使系统降阶为平面虚拟Pendubot。其次，基于平面Pendubot 幂零近似特性，设计一个周期性开环迭代控制器，使平面虚拟Pendubot 两连杆的角速度为0 的同时，第一连杆回到目标位置，使原系统降阶为所有连杆初始角速度为零的平面虚拟Acrobot。根据平面Acrobot 的运动状态约束关系，以及系统末端点坐标位置和连杆之间的约束关系，利用粒子群优化算法计算第二连杆和第三连杆目标角度。最后，针对第三连杆控制目标设计控制器，实现平面虚拟Acrobot 的控制目标，从而实现平面APA系统的控制目标。

1 系统建模

平面APA系统的模型如图1 所示。图中，mi为第i(i= 1,2,3 )杆的质量，Li为i杆的长度，Lci为i杆的质心到前一关节的长度，Ji是i杆的转动惯量。

根据欧拉-拉格朗日法建立系统的动力学方程为：

如图1 所示，设欠驱动关节的位置为(XP,YP)，则欠驱动关节与系统末端点的几何约束关系为：

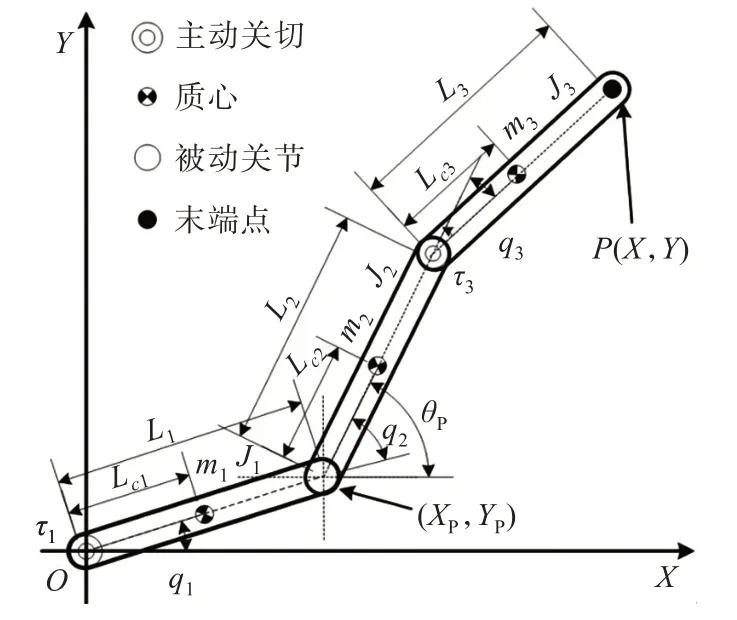
图1 平面APA 系统Fig. 1 Planar APA system

其中，XP= -sinq1L1，YP= cosq1L1，θP=q1+q2。

2 平面虚拟Pendubot控制

将平面APA系统降阶为平面虚拟Pendubot，并实现欠驱动关节位置控制目标。

2.1 第一连杆目标角度求解

根据系统的目标位置来求解系统第一连杆的目标角度。 以平面APA系统目标位置为圆心(xd,yd)，平面虚拟Acrobot 两连杆杆长之和为半径，构建一个圆C1；以平面APA系统首关节为圆心，平面虚拟Pendubot 驱动连杆杆长为半径，构建另一个圆C2；可得：

圆C1与圆C2的交点A(x1,y1)、B(x2,y2)为欠驱动关节目标范围的极限位置。欠驱动连杆目标角度的范围在qd1∈[ arctan (y1/x1), arctan(y2/x2)] 内就能保证平面APA系统末端点目标位置在几何可达范围内。

2.2 原系统降阶为平面虚拟Pendubot

控制第一连杆达到目标角度，同时控制第三连杆的角度和角速度为零。

根据控制目标和平面APA系统的状态空间方程［10］，构造Lyapunov 函数V1( )

x：

其中，e1和e2为正数。

当连杆状态满足条件S1时，平面APA系统被降阶为一个欠驱动关节速度不为零的平面虚拟Pendubot。因此，需要对平面虚拟Penduobt进行稳定控制。

2.3 平面虚拟Pendubot稳定控制

为维持第二连杆与第三连杆为一根虚拟连杆，τ3持续保持式（10）对第三连杆持续进行控制作用。

基于以上分析，可得平面虚拟Pednubot 的部分反馈线性化形式为：

式中，N= (m2+m3)L1Lc1/(J˜2+ (m2+m3)(Lc2+Lc3)2)。

模糊规则如表1 所示。

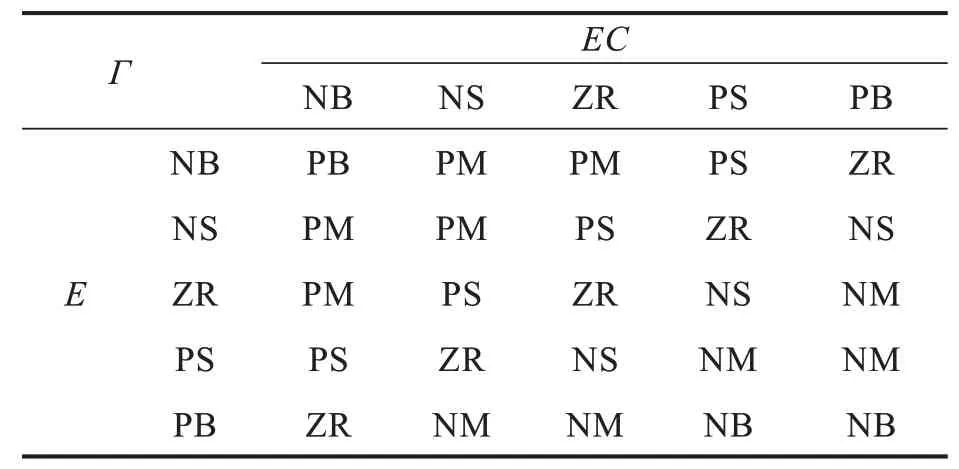
表1 模糊控制规则Tab. 1 Rules of fuzzy control

将系统总输出乘以比例因子Γ=kout·η代入开环迭代镇定控制器中。经过镇定控制的平面虚拟Pendubot 达到控制目标时可以进行切换。定义切换条件S3为：

当平面APA系统连杆的状态满足切换条件S3时，就可以被降阶为初始速度为零的平面虚拟Acrobot。

3 平面虚拟Acrobot控制

根据平面虚拟Acrobot 驱动连杆与欠驱动连杆的角度约束关系设计稳定控制器。根据平面虚拟Acrobot 的位置控制目标和几何约束关系，利用粒子群优化算法获得对应两杆的目标角度。

3.1 平面虚拟Acrobot模型

3.2 基于粒子群算法的目标角度求解

根据平面虚拟Acrobot 的位置控制目标，用粒子群算法［15］进行计算其目标角度。目标函数可以定义为：

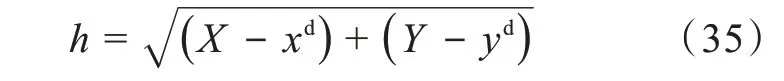
式中，(xd,yd)为平面虚拟Acrobot 的末端点目标位置，P(X,Y)为系统末端点位置，由式（2）计算可得。求解目标角度的算法步骤如下：

Step1：初始化粒子的初始位置与初始速度；

Step2：根据式（2）和式（35）计算适应度函数h；

Step3：当h( · )≤e3时，可得第三杆目标角度，否则，转到第二步；

Step4：将第三杆目标角度代入根据角速度约束关系，求出欠驱动连杆的目标角度。

3.3 平面虚拟Acrobot系统控制器设计

根据控制目标，构造Lyapun ov 函数V2(x)：

依据LaSalle 不变原理，可得xi→qid，xi+3→0。则式（37）能实现平面虚拟Acrobot 的控制目标。

4 仿真实验研究

利用MATLAB 数值计算工具验证提出的控制策略的有效性，平面APA系统的模型参数如表2所示。

表2 平面APA 系统模型参数Tab. 2 Model parameters of planar APA system

系统的初始状态为：

如图2 所示，角度、角速度都收敛到目标状态，末端点也稳定到目标位置。系统驱动杆的驱动力矩始终保持在20 N·m 以内，力矩较小。在13.17 s时，系统从第一阶段切换到第二阶段；在23.67 s时，系统从第二阶段切换到第三阶段；在33.79 s时，系统各连杆均到达目标角度，从而平面APA系统末端点也到达目标位置。

图2 仿真结果：（a）角度，（b）角速度，（c）控制力矩，（d）位置Fig. 2 Simulation results：（a）angle，（b）angular velocity，（c）control torque，（d）position

5 结 论

针对平面APA系统末端点位置控制问题，本文提出了一种基于模型降阶的控制策略。将平面APA系统末端点位置控制问题转化为平面虚拟Pendubot 的稳定控制问题和平面虚拟Acrobot 的位置控制问题。首先，基于开环迭代控制实现平面虚拟Pendubot 的稳定控制。其次，针对平面虚拟Acrobot，借助角度约束关系，采用粒子群算法计算各连杆角度，直接控制驱动连杆到达目标角度，并间接实现欠驱动连杆的控制角度目标，并最终实现平面APA系统末端点位置控制。