悬挑梁对结构受力特性影响分析

盛 唤，周万清*

1. 防灾减灾湖北省重点实验室（三峡大学），湖北 宜昌443002；2. 三峡大学土木与建筑学院，湖北 宜昌443002

随着经济蓬勃发展和科学技术不断更新，充分利用空间资源，设计出创造性建筑外观的悬挑结构越来越受到青睐［1］。但悬挑结构对结构整体的抗震很不利［2］，悬挑梁构件所受的内力复杂，构件在地震作用下的抗震性能有待分析［3］；现行结构设计规范对悬挑构件没有特别明确的规定［4］，设计院通常根据经验进行配筋设计［5］；并且只对悬挑梁单一构件和只使用一种软件进行分析，缺少运用多种有限元软件的悬挑结构整体分析［6-7］。作者基于两种不同的有限元软件对外围有悬挑梁和无悬挑梁的建筑结构，在风荷载和水平地震作用下［8］，采用结构 分析软件SAP2000（structure analysis program 2000，SAP2000）反应谱分析方法和高层建筑结构空间有限元分析软件SATWE（space analysis of tall-buildings with wall-element，SATWE）弹性分析方法进行对比验算，得出框架结构在两种情况下的自振周期［9］、结构变形倒塌的轴压比和水平荷载作用下的层间位移比［10］，保证其抗侧位移构件布置合理且有效，分析计算结果的差异性。

1 工程概况

该商业楼为客运中心，建筑总体平面布局采用矩形，东西长41.8 m，南北长25.8 m，商业裙房部分预留大空间，首层平面图如图1 所示。总建筑面积为3 332.00 m²，共3 层，建筑高度为13.95 m。结构采用钢筋混凝土框架结构体系，剪力墙分布在电梯井处，安全等级为二级，基础设计等级为丙级，建筑防火等级为二级。建筑抗震设防类别为丙类，抗震设防烈度为Ⅵ度（0.05g）。结构抗震等级［11］：框架结构设置四级抗震，剪力墙设置三级抗震。基本风压0.3 kN/m²，基本雪压0.3 kN/m²。地基承载力特征值fak=400 kPa。主体结构混凝土强度 等 级 为C30，容 重25 kN/m3。 钢 筋 等 级 为HRB400，楼板厚为120 mm。计算罕遇地震作用时，考虑偶然偏心，周期折减系数0.7，特征周期0.4 s，梁端负弯矩调幅系数0.85，梁扭矩折减系数0.4，梁刚度放大系数取2，柱按双偏压计算，考虑重力二阶效应。主要荷载：主梁10.6 kN/m，次梁11 kN/m。玻璃幕墙、女儿墙线荷载分别为6 和8 kN/m。 其他荷载参考《建筑结构荷载规范》（GB50009-2012）。

2 方案确定

原方案结构初步设计有2 种方案：第1 种是无悬挑结构方案，如图1 所示；第2 种是将外围边柱向内移动900 mm，采用悬挑结构。

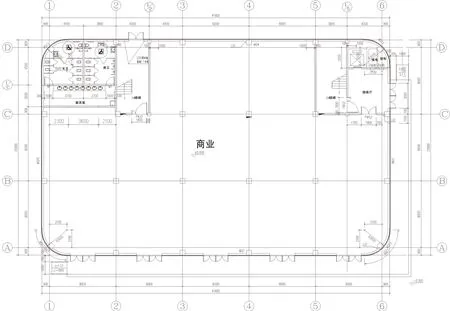
图1 首层平面图Fig. 1 Ground floor plan

2.1 梁控制参数

根据悬挑梁所承受的恒活荷载，分别采用SAP2000 软件及SATWE 软件对框架结构进行建模分析，计算水平风荷载和罕遇地震作用下主体结构的稳定性情况。各种梁的截面如下：主梁截面尺寸分别250 mm×700 mm/900 mm/1 200 mm，350 mm×700 mm/900 mm/1 200 mm，300 mm×800 mm。次梁截面尺寸分别250mm×500mm/700mm，300 mm×700 mm。 柱 截 面 尺 寸 分 别400 mm×400 mm ，500 mm×500 mm，600 mm×600 mm，450 mm×450 mm。本文对整栋建筑仿真分析着重于悬挑梁结构对整体结构受力性能的影响［12］。

2.2 多遇地震风荷载

风荷载标准值按公式ωk=βz×μz×μs×ω0进行计算［13］。风荷载作用下层间侧移

地震反应谱［14］分析本质上是一种拟动力分析，利用动力方法对质点地震响应进行计算分析，并使用统计的方法形成反应谱曲线，然后利用静力方法进行结构分析，计算每个振型中的位移内力的最大值。反应谱分析公式：

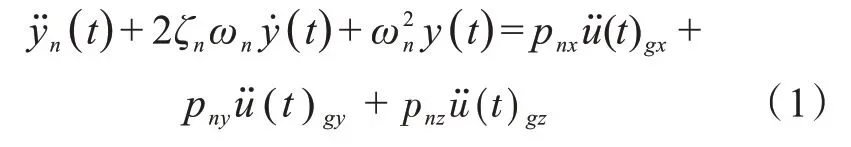
式（1）中3 个振型参与系数是由pni=-ϕnTMi定义的，i为x、y或z，式（1）考虑了结构3 个方向上的地震作用。反应谱分析是基于方向组合求解结构的总响应，当只考虑1 个方向上的地震作用时，式（1）可变为式：

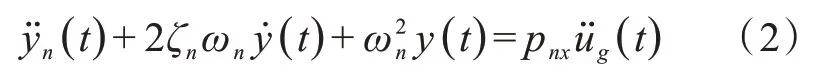
由式（2）可绘制出最大值响应ymax(ω)的曲线，对于该加速度输入，根据定义得到反映地震作用的位移变化。图2 表示反应谱曲线图。

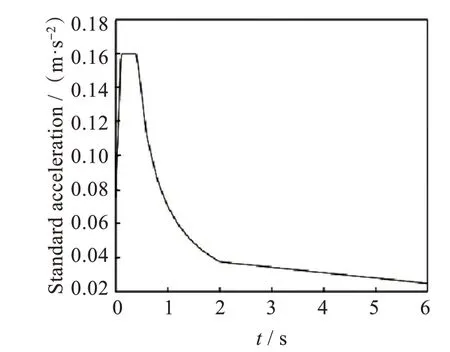
图2 地震反应谱图Fig. 2 Seismic response spectrum

3 结果与讨论

3.1 SAP2000 建模分析

利用SAP2000 软件对有悬挑梁和无悬挑梁的主体结构进行建模，悬挑梁和主体结构用Frame 单元模拟，根部完全嵌固［15］，运用Plane frame 分析模式，得到相应的结果。图3（a）为带悬挑梁框架整栋模型图，图3（b）为无悬挑梁的框架整栋模型图。

图3 框架模型图：（a）带悬挑梁，（b）无悬挑梁Fig. 3 Frame models：（a）with cantilever beam，（b）without cantilever beam

3.2 结构周期比

结构振动周期计算结果如表1 所示。《高层建筑混凝土结构技术规程》规定［16］，周期比指结构扭转为主的第一自振周期Tt与平动为主的第一自振周期T1之比，A 级高度高层建筑不应大于0.9，B 级高度高层建筑、超过A 级高度的混合结构不应大于0.85。根据周期比的定义得出无悬挑梁时的周期比为0.807，有悬挑梁时的周期比为0.889。有悬挑梁的构件第一平动周期和第一扭转周期都较无悬挑梁时大。表明有悬挑梁的周期比值较大，抗扭刚度变弱，扭转位移角也越大，使得整体结构变柔。

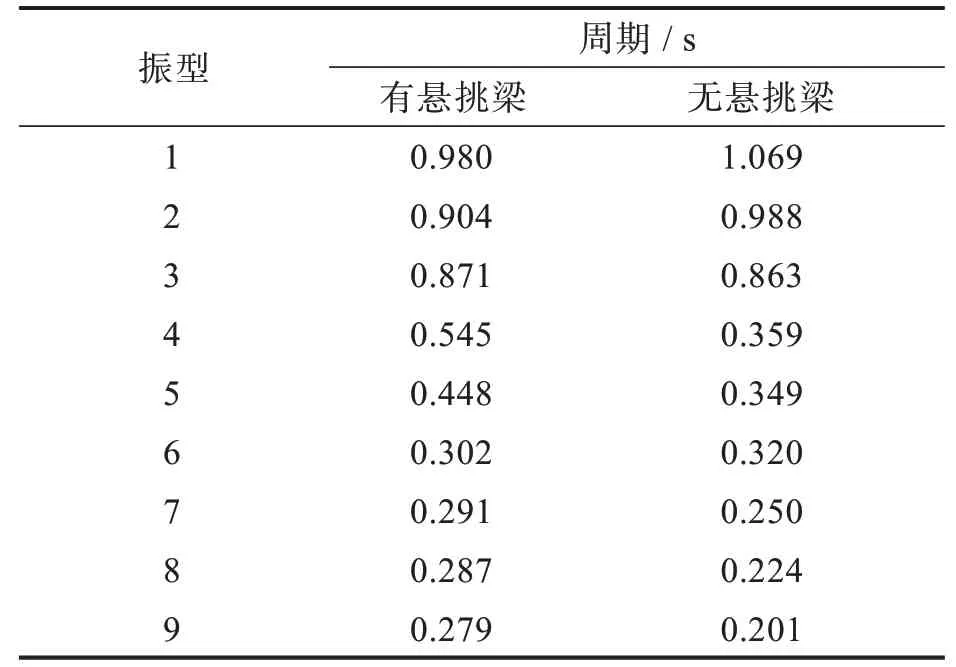
表1 各振型的周期Tab. 1 Period of each vibration mode

3.3 结构轴压比

A、B轴两榀框架的轴压比，如图4 所示。轴压比指柱考虑地震作用组合的轴压力设计值与柱全截面面积和混凝土轴心抗压强度设计值乘积的比值。柱的截面尺寸为500 mm×500 mm，从A、B轴两榀框架柱的轴压比设计结果对比可以得出：有悬挑梁时比无悬挑梁时大；B轴无悬挑梁时轴压比大，说明柱承受的荷载大，悬挑梁对柱的影响大。结构设计时柱距相同，通过提高混凝土的等级和增大柱的截面尺寸来保证结构的轴压比满足规范要求，因为增强柱的承载能力可以防止出现混凝土被压碎而产生脆性破坏的现象。

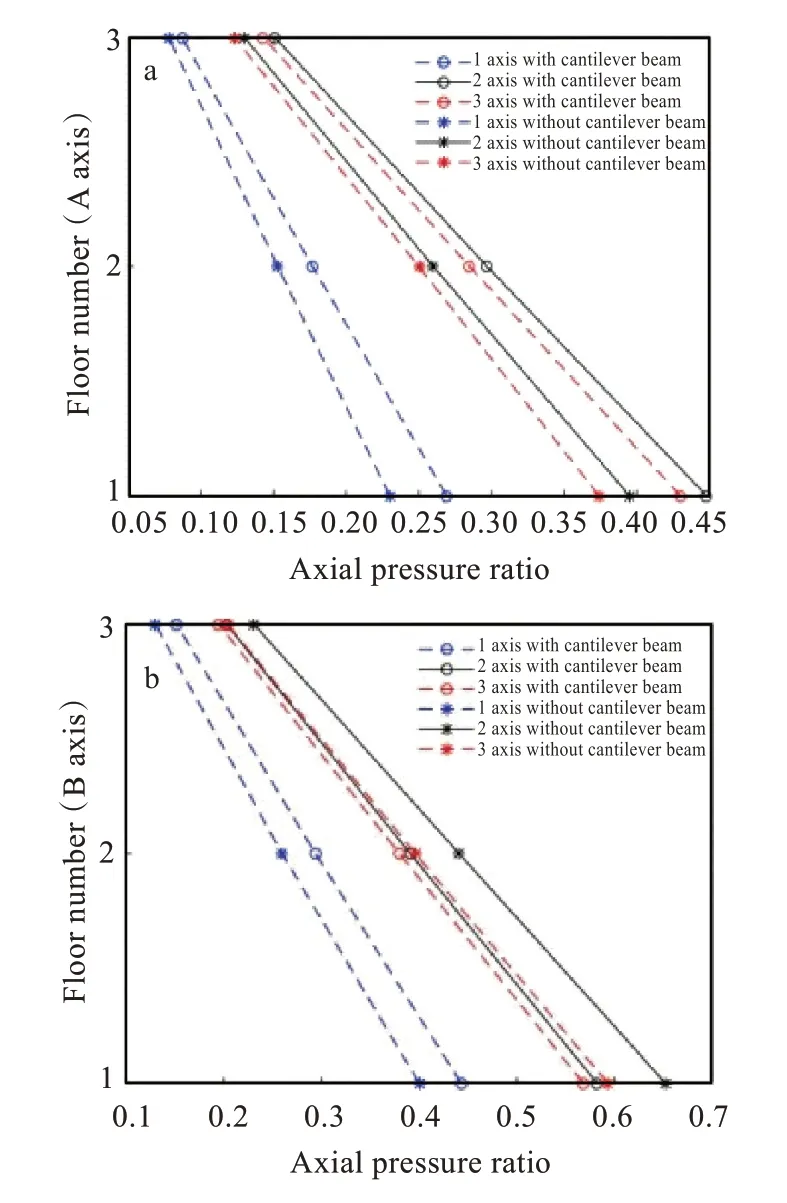
图4 框架柱轴压比图：（a）A 轴，（b）B 轴Fig. 4 Axial compression ratio of frame column：（a）A axis，（b）B axis

3.4 楼层位移

利用SAP2000 反应谱地震分析X，Y方向的层间位移。表2为X向和Y向地震工况的位移比，图5为前三层和楼梯出屋面的最大楼层位移图。

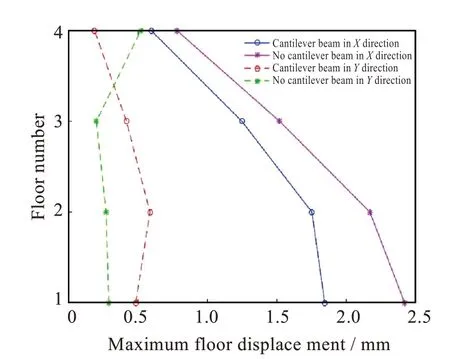
图5 X，Y 向地震工况的最大楼层位移Fig. 5 Maximum floor displacement of seismic conditions of X and Y direction

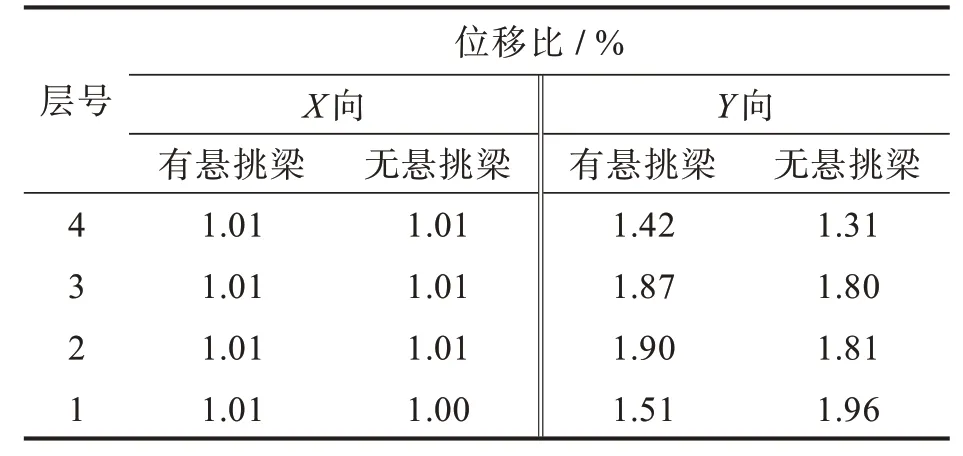
表2 X 向和Y 向地震工况的位移比Tab. 2 Displacement ratio of seismic conditions of X and Y direction

框架结构1 层到3 层都是由玻璃幕墙组成的外围整体，风荷载直接作用在幕墙上，有悬挑梁最外围围绕一圈封口梁，玻璃幕墙的荷载直接作用在封口梁上。导致在水平地震和风荷载作用下，X，Y方向上的层间位移有不同程度的变化，有悬挑梁时结构Y方向位移比增大，其中2 层变化0.09%，3 层变化0.07%，4 层变化0.11%，得到结构的最大层间位移和其变化趋势为上大下小，建筑整体侧向刚度偏小［17］，出现该情况的原因是层间位移角过大，结构过柔。通过改变结构平面布置调整为无悬挑梁的结构，使其变成一个规则图形减小结构刚心和质心的偏心距，让位移比满足要求。SAP2000 分析结果表明，悬挑梁对结构在水平荷载作用下的层间位移影响很大。

在地震作用下，利用反应谱分析法得出结构在有悬挑梁时的水平方向层间位移的变化趋势较大，其中Y方向上的顶层层间位移幅度变化明显。满足结构规范和工程师的需求的拟动力分析［18］，计算质点地震响应形成反应谱曲线使用静力方法分析，得到结构的最大层间位移和构件的最大值，更为方便地进行结构设计。

3.5 SATWE 结果分析

SATWE 软件建模分析结果表明，有无悬挑梁两种结构的周期比都为0.778，都小于0.9，符合规范中对于结构构件满足一定扭转刚度的要求，与SAP2000 的结果相比存在差异。对比这两种软件模拟得到的周期比，无悬挑梁时周期比相差0.029，有悬挑梁时周期比相差0.111，表明不同软件计算的周期比存在差异，原因是SAP2000 适用于钢结构设计，而SATWE 计算得出的结果接近实际情况。SAP2000 计算在地震作用下，有悬挑梁周期为0.889，接近0.9，只有控制好结构的抗扭刚度，使Tt/T1值处于理想的区间值，才能使结构具有一定的抗扭刚度，保证结构在地震作用下的抗扭能力和结构的抗震安全性。可以看出有悬挑梁存在的结构中以扭转为主的第一自振周期偏小，反而平动周期变化不大，得到悬挑梁的存在影响结构的扭转刚度。在实际设计中若存在悬挑梁且周期比过大，可以通过增加质心和刚心的偏离程度或者增加结构周边抗侧构件刚度来调整周期比［19］，使之满足要求。

悬挑梁的存在对结构的轴压比影响不大，且在限定的轴压比（＜0.9）范围内，但是在结构突变处柱的轴压比变化明显。在保证整体结构的延性方面［20］，柱的塑性变形能力和框架结构整体在罕遇地震下倒塌能力都满足要求。利用两种不同软件计算得出整体框架结构的轴压比相差不大，在分析轴压比的差异性上两种软件都可行，说明悬挑梁对整个构件抗倒塌能力和保证塑性变形能力的影响不大。

在地震作用下，有悬挑梁时X方向的位移比系数为1.06%，Y方向为1.01%；无悬挑梁时Y方向的位移比系数为1.04%，X方向为1.03%，可以看出楼层之间的刚度和扭转变化情况相对稳定，且框架结构的X、Y方向水平位移变化不大，构件基本不会出现过大的偏心及过大的扭转效应。同时计算结果表明整体最大层间位移角变化不大，说明按弹性分析计算方法有无悬挑梁的框架结构在刚度和构件的截面尺寸方面均满足。SATWE 依照中国规范编写，在结构平面布置规则有无悬挑梁的条件下，SATWE 分析的构件的X方向和Y方向水平位移比SAP2000 计算的水平位移都要大，产生过大的偏心而导致结构产生较大扭转效应，可以得到SATWE 计算的结果更加真实，其结果可信度更高。为了保证整个框架构件的整体稳定性，可以利用反应谱分析方法验算结构位移变形。

4 结 论

1）本文采用SAP2000 和SATWE 有限元软件，利用反应谱分析、弹性分析的分析方法分析悬挑梁对结构的影响，得到有悬挑梁的周期比大于无悬挑梁的周期比，周期比控制并不一定要求结构足够结实，而是要求结构布置的合理性；悬挑梁对轴压比影响不大，但是在结构布置突变处柱的轴压比增大，需要注意相应位置柱的轴压比并进行调整；有悬挑梁Y方向的位移比、最大层间位移都较无悬挑梁时大，可以增大柱截面或提高混凝土等级使整体结构满足安全性。根据实际施工方便性，参考部分多遇地震分析的数据，最终方案设计为在框架结构四级抗震和剪力墙三级抗震设计选择无悬挑梁的框架结构，使得结构布置规则。

2）客运站外围设置悬挑梁为了建筑形式美观要求。而对于多层或高层建筑上，对于外围悬挑又有玻璃幕墙的建筑结构，在水平风荷载、地震作用下的整体安全性能方面仍需要进行更深一步的研究探索。本研究中使用了两种软件分析悬挑梁的不规则受力的特点，结果表明SATWE 法较SAP2000 法更加准确和实用，有助于相同客运站工程借鉴使用。