多变量分数阶微分系统的稳定性分析①

王雪芹, 李晓艳, 陈雨婷

(安徽大学数学科学学院,安徽 合肥230601)

0 引 言

随着非奇异核分数阶导数的兴起,许多学者致力于含有非奇异核分数阶系统的研究[1-9]中去。其中,多变量分数阶系统的稳定性分析更成为一个难点问题,目前也已取得了一定的成果[10-12]。在前人工作的基础上,主要利用一个新的比较原理,结合李雅普诺夫方法,通过构造一个已知渐近性结果的分数阶系统,利用其渐近稳定性确保原分数阶系统的渐近稳定性。将考虑如下多变量分数阶微分系统:

或其矩阵形式为

1 预备知识

在本节中,将给出一些重要的定义与引理,具体的可参照相关文献[5,6,7,9]。

定义1.1[6,7]函数f(t)是[0,b]上的可微函数,并且f'∈L1(a,b)。则其ABC-分数阶导数定义为:

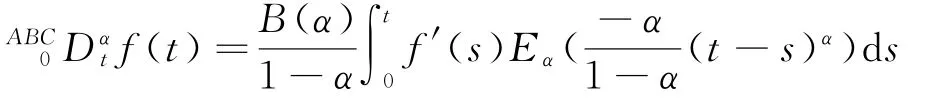
其中0＜α＜1,0＜t＜b,B(α)代表标准化函数。定义中的Eα代表单参数的Mittag-Leffler函数,单参数和双参数的Mittag-Leffler函数分别定义为

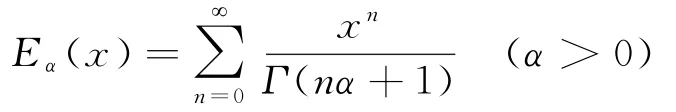
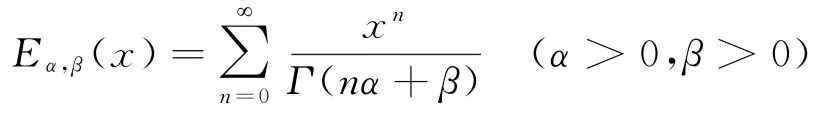
定义1.2[6,7]ABC-分数阶导数和双参数的Mittag-Leffler函数的Laplace变换定义为:

引理1.3[5]设x(t)∈ℝn是连续可微的向量函数,P∈ℝn×n是对称正定的常矩阵,则有:

引理1.4[9]给定α∈ℝn,β∈ℝn,则有如下关系式成立:

2 主要结论

本节利用数学归纳法得到推广的比较原理,并运用李雅普诺夫方法,得出主要内容。

引理2.1(比较原理)考虑下列的分数阶微分不等式

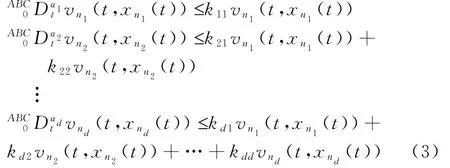
其中0＜αi≤1,i=1,2,…,d。与之相对应的比较分数阶微分系统为

初值条件为v ni(0,x ni(0))≤u ni(0,y ni(0)),i=1,2,…,d。其中k ii＜0,i=1,2,…,d,并且k ij≥0,i＞j。则 有v ni(t,x ni(t))≤u ni(t,y ni(t)),i=1,2,…,d。

证明:(i)当i=1时,从(3)中可以得到,存在非负函数m n1(t)使得

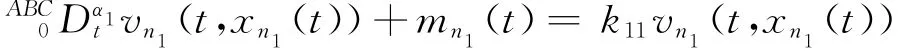
上式两端Laplace变换可得

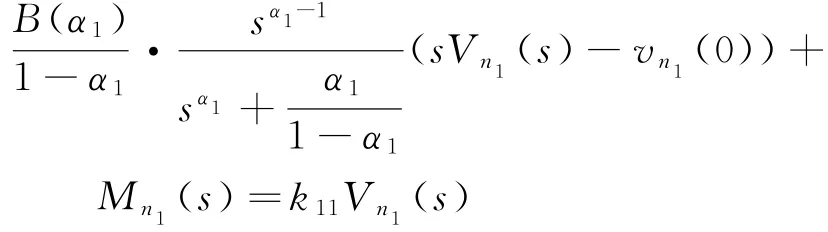
其中V n1(s)=L{v n1(t,x n1(t))},v n1(0)=v n1(0,x n1(0)),M n1(s)=L{m n1(t)},整理得

从(4)中可以得到

由(5),(6)和初值条件可得

(ii)假设当i=d-1时,有

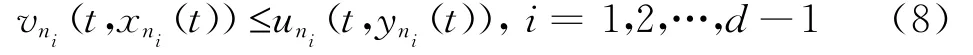
当i=d时,存在非负函数m n d(t)使得

所以

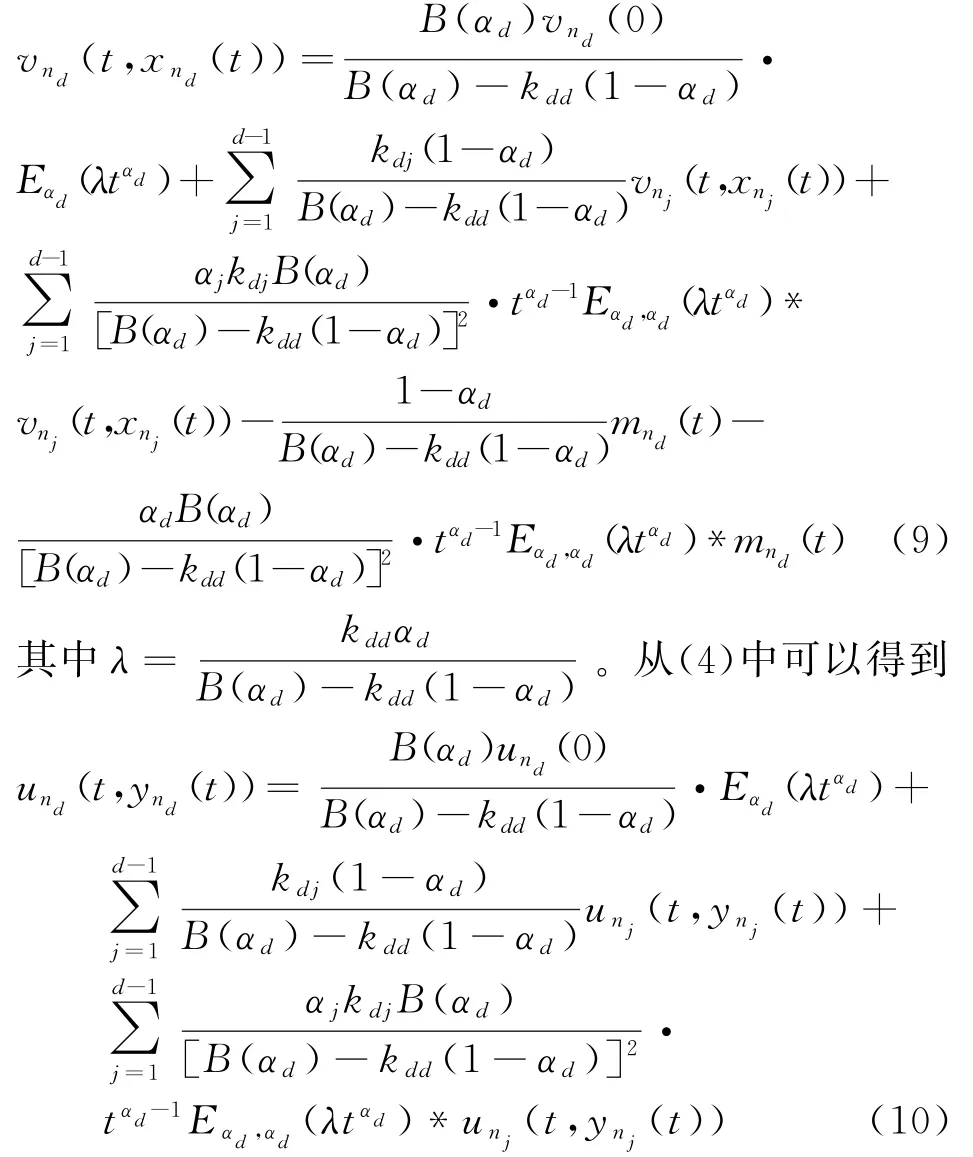
由(8),(9),(10)和初值条件可得

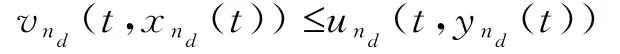
由归纳假设可知,结论成立。证毕。

接下来,给出的两个引理[10,11]对我们得出的稳定性结果是至关重要的。

引理2.2[10]若系统(1)的特征方程det[Δ(s)]=0的根均具有负实部,则系统(1)的零解是渐近稳定的。其中

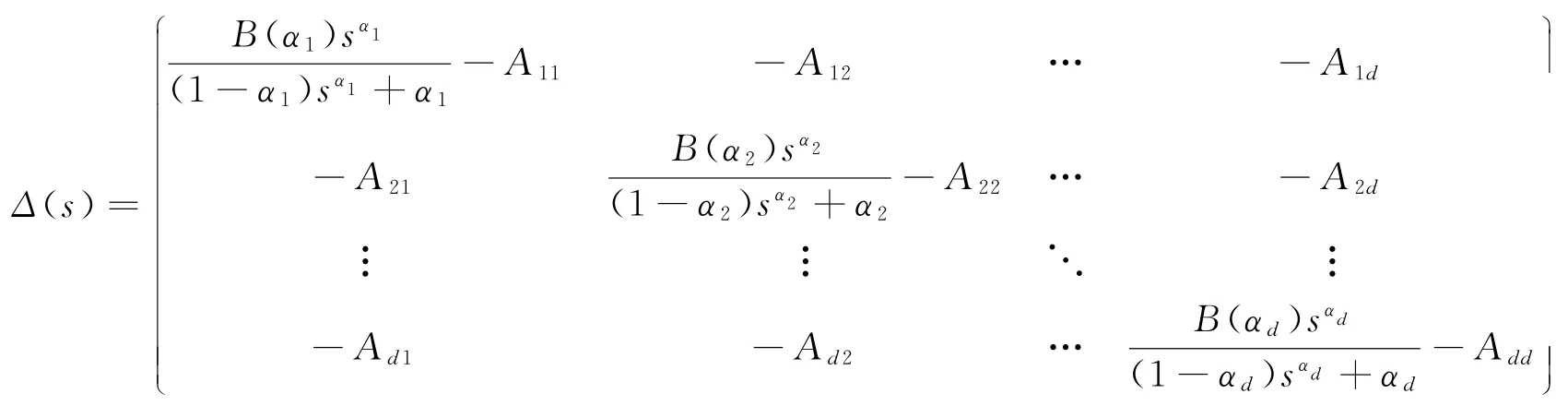
引理2.3[11]假定系统(1)的系数矩阵A∧是分块上三角或分块下三角矩阵,且每一个对角元均具有负实部。则系统(1)的零解是渐近稳定的。

定理2.4若存在对称正定矩阵P ni∈ℝni×ni使得下列条件成立,则系统(1)的零解是渐近稳定的:

(iii)(11)式的根均具有负实部

其中P ni∈ℝni×ni是对称正定矩阵,I ni∈ℝni×ni,I n j∈ℝn j×n j是单位矩阵。

证明:首先构造Lyapunov函数V(t)=,其中是连续可微的二次函数,由引理1.3可得

则可以得到

初值条件为U ni(0)=V ni(0),i=1,2,…,d。由引理2.1可得V n i(t)≤U ni(t),i=1,2,…,d。

在条件(iii)下,可得系统(14)的零解是渐近稳定的,即有所以有

定理2.5若系统(1)的系数矩阵是分块下三角矩阵,即A ij=O,i＜j。若存在对称正定矩阵P n i∈ℝni×ni使得下列条件成立,则系统(1)的零解是渐近稳定的:

3 结 语

利用推广的比较原理,通过构造一个已知渐近性的分数阶系统,根据其渐近稳定性保证原分数阶系统的渐近稳定性。结合连续可微二次函数的ABC-分数阶导数,和文献[10,11]中的稳定性原理,得到了含有ABC-分数阶导数的多变量系统的稳定性结果。同时,也为我们研究具有非奇异核的分数阶算子的稳定性提供了一种新的方法。