基于测不准原理的一维谐振子势中粒子能级及概率的讨论①

代君瑶, 张澜旭, 温 莹, 张海丰,*

(佳木斯大学1.理学院,2.机械工程学院,黑龙江 佳木斯154007)

在量子理论的研究和应用中,一维谐振子模型和测不准关系是非常重要的物理模型和重要理论,它们在理论研究和计算物理中都有广泛的应用。例如:乔流飞等利用代数解法讨论了一维电谐振子能量本征问题[1];冯璐等给出了电磁场中线性谐振子本征能量和本征波函数[2];赵森等研究了均匀电磁场作用下的一维线性谐振子的能级分布[3];肖奎等对一维线性谐振子本征矢及概率进行了可视化分布演示[4];刘燕杰论述了测不准原理的应用范围和意义[5];张佳林讨论了微观粒子波粒二象性和测不准原理的联系[6];沈曼等从坐标和动量的测不准关系出发对线性谐振子模型进行了分析[7];张艳燕等对测不准原理和表象理论进行了讨论[8];周宙安等利用测不准原理讨论了位置物理量算符的最小不确定度[9];陈念陔等分析了当前理论研究领域对测不准原理的研究[10];周宙安等探讨了测不准原理下的光频的引力红移问题[11]。本文旨在通过测不准原理,讨论一维谐振子势场中粒子出现的概率,进而对基态能级问题进行详细的分析。

1 一维谐振子的能级

设质量为m,角频率为ω的一维谐振子的势能函数为

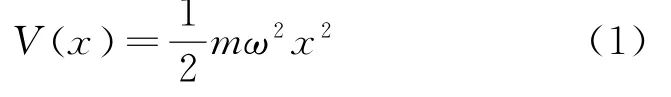
则体系的哈密顿算符和本征方程可以写成

于是得到

或

当ζ取值较大时,上式变为

于是按照波函数的自然条件可以得到上式的渐进解

所以本征波函数可以表示为

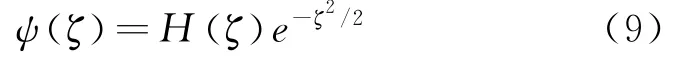
上式带入本征方程可得

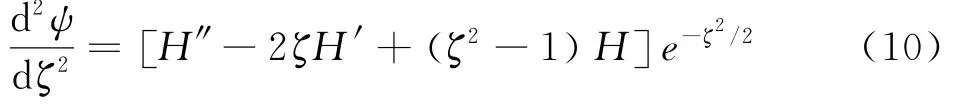
厄米多项式微分方程为

在ζ=0附近可以得到级数展开式

所以系数应该满足

由于级数的所有系数都必须是零,即

即

根据波函数的有限性条件,截取前n项,令H n（ζ）的系数为零,可以得到

所以,能级表示为

可见,能量本征值是量子化的。在没有外界能源情况下,体系在温度T=0时具有最小能量本征值。

2 粒子出现的概率

设一维谐振势下,一个粒子具有能量E0=ћω/2,下边我们讨论粒子在经典禁区出现的概率,并将其与粒子出现在更高能级的概率进行比较。

按照经典理论,经典谐振子满足

所以能量可以表示为

对于基态可得

令η=x/λ,则有

取A0/λ=1,则

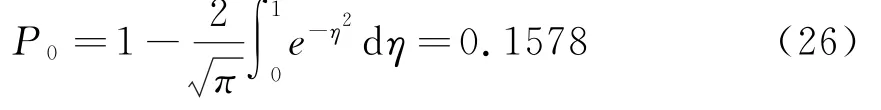
对于其他高能级激发态,相应的概率为

即

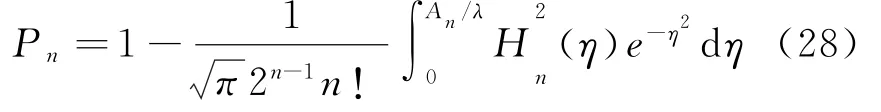
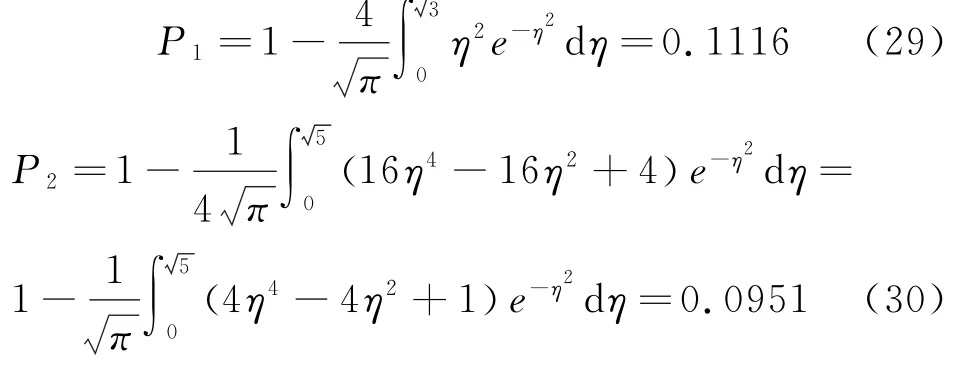
可见,对于各个能级的概率P n,能级越高它的值越小,究其原因在于能量高低决定了哪种粒子更趋于“经典”,即具有较高能量的粒子出现在经典禁区的概率较小。

3 应用测不准关系讨论基态能级

下边根据坐标和动量的测不准关系ΔpΔx≥ћ/2来近似求解一维线性谐振子的基态能级。

根据(2)式可以得到体系哈密顿量的在任意态上的平均值

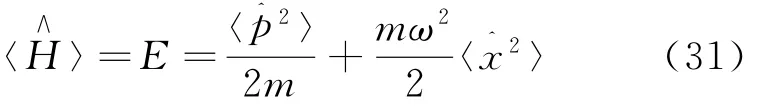
按照算符差方平均值定义,可得坐标和动量算符的差方平均值分别为

根据谐振子的势能函数具有空间反演对称性,所以

于是,得到

由于

根据ΔpΔx≥ћ/2可知,Δp的最小值为,则上式变为

再对上式求E（Δx）的最小值,即求一阶导数等于0

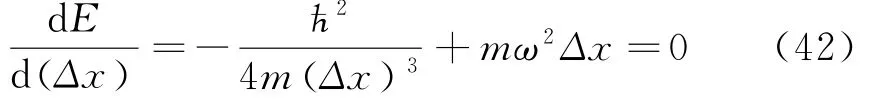
所以可得

4 结 论

通过上边的讨论,可以看到,通过代数解法给出的精确解与用测不准关系近似求解的一维线性谐振子基态能级是一样的,且粒子在谐振子基态和前两个激发态上的概率分别为0.1573,0.1116,0.0951,这表明能级越高粒子出现的概率越小,粒子越趋于“经典”特性。