嵌入四分之一正交学习的人工蜂群算法
2021-11-01宋晓宇全鹏宇肖以筒
宋晓宇,全鹏宇,赵 明,肖以筒
(沈阳建筑大学 信息与控制工程学院,辽宁 沈阳 110168)
0 引 言
人工蜂群算法(artificial bee colony algorithm,ABC)[1,2]在解决持续优化问题方面有着优秀的表现,近些年来受到广泛关注。然而,ABC算法有着探索能力强但开发能力弱[3]的问题,这主要受制于ABC算法每次只改一维的搜索模式[4,5]。根据没有免费午餐定理(no free lunch,NFL),每种算法都有各自的优劣,将ABC算法与其它开发能力强的辅助方法相结合,达到优势互补的效果,这是提升ABC算法开发能力的一种切实可行的方法。
正交实验设计(orthogonal experimental design,OED)因可以通过少量实验样本发现不同因素的最佳组合水平的能力而被广泛使用。其中,正交学习(orthogonal learning,OL)使用正交实验设计构造一个有潜力的候选解来加快算法的收敛速度,取得不错的效果。然而,OL仍存在着改进效率低和由于一次改进全部维导致的种群多样性下降快的问题。
针对这些问题,本文以OL为基础,根据2水平正交表的特点对参与正交的维数提出改进,不再使用全部维参与正交学习,而是选取一次正交实验使用相同评价次数可以修改的最大维数,最高效地利用函数评价次数。此外,本文还提出一种精英解引导的维选择方法,将其与随机选择结合,能够在保持探索能力的同时加快进化速度。
1 人工蜂群算法
1.1 基本的ABC算法
人工蜂群算法是一种基于群体的随机优化方法,其灵感来自于蜜蜂的摇摆舞和智能觅食行为。ABC算法有3种蜜蜂,雇佣蜂、观察蜂和侦查蜂[6],雇佣蜂数量等于观察蜂,且等于食物源数量。雇佣蜂负责探索食物源和收集有用的信息。观察蜂负责开发好的食物源,食物源的质量越高被搜索的机会就越大。如果一个食物源在一定次数内无法被提升,那么它的雇佣峰就会被一个新产生的侦查蜂替代。
在ABC算法中,一个食物源代表一个解,食物源的质量代表搜索过程中一个解的适应性。SN代表食物源的数量,max_FEs为函数最大评价次数,trial记录相应个体连续失败更新的次数。limit为启动侦查蜂的限制值。
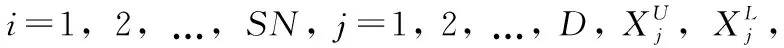
(1)
然后,使用式(2)计算食物源的适应值
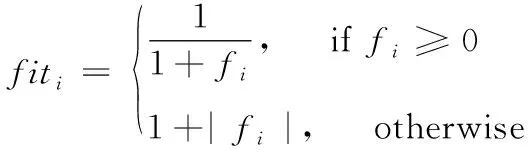
(2)
其中,fiti是第i食物源Xi的适应值,fi是食物源Xi对于优化问题的目标函数值。
在雇佣蜂阶段,每一个雇佣蜂用搜索方程在自己的食物源附近搜索并寻找更好的食物源,搜索方程如式(3)所示
Vi,j=Xi,j+φi,j·(Xi,j-Xk,j)
(3)
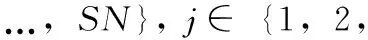
在观察蜂阶段,雇佣蜂分享食物源信息,优质的食物源会吸引更多的观察蜂。然后,观察蜂选择一个食物源进行搜索,第i个食物源被选中的概率为pi,pi通过式(4)计算
(4)
被选中的食物源使用式(3)生成一个新的候选解,如果候选解的适应值优于原解,则替换原解,并且其计数器将重置为0。否则,trial加1。
在侦查蜂阶段,选择计数最高trail的食物源。如果其trail大于预设的limit,该食物源将被其所使用的蜜蜂放弃,然后其雇佣峰将成为一只侦察蜂,使用式(1)寻找一个新的食物源,并且其trail值被重置为0。
算法的终止条件为找到可接受解或评价次数达到max_FEs。
1.2 ABC的改进工作
ABC算法自提出以来,许多研究人员开展了提升ABC算法性能的相关工作。有关结合辅助方法和有关维的选择方面研究的简要概述如下所示:
(1)结合其它辅助方法。Li等[7]提出记忆机制来指导搜索。Li等[8]受基因重组的自然现象启发提出了GRO方法。Xiang等[9]通过引入重力模型来选择优质的邻居用于引导搜索;
(2)有关维的选择。Zhang等[10]提出更新时对所有维测试,找出最好的维,产生候选解。Loubiere等[11]使用敏感分析方法提出了Morris方法,通过计算每一维对目标函数的影响,控制维度选择。Kong等[12]提出ECABC算法同时改进一个解的两维。
2 提出的QOL方法
2.1 动 机
基本ABC算法的搜索是每次只改进1维,导致收敛速度慢。通过增加一个解改进的维数可以加快解的收敛速度,而正交实验可以通过少量评价次数来修改一个解的多维。OL使用了正交实验取得一定的效果,但仍有很大的改进空间。为了提升OL的改进效率,本文根据2水平正交表的特点,每次正交实验需要的评价次数如式(5)所示。根据该公式,可以控制n的取值,从而限定m的数值,来最高效地利用函数评价次数,进而提升改进效率。例如,当n∈[8,15]时,m的值为16,故当n=15时就可以最大化利用这16次评价
(5)
此外,确定改进的维数后,需要一个方法选出哪些维参与正交实验。基本ABC算法的选维是随机的,这种方法更倾向于探索。为了提升开发能力,本文提出一种将引导和随机选择相结合的选维方法。一部分维利用精英解引导选择,选取与精英解均值差距大的维进行改进,来提升开发能力。另一部分采用随机方式选取,保证每个维都有被选中的机会,保持探索能力。
2.2 QOL方法
基于以上考虑,本文提出两种方法QOL(四分之一正交学习)和HOL(二分之一正交学习)。QOL和HOL和使用式(6)计算要改进的维数n,在QOL中p=4,在HOL中p=2。通过实验验证QOL略优于HOL,相应实验结果及分析可见本文实验分析部分。值得一提的是,p=8等虽然也能高效利用评价次数,但其维数所占整体的比例过小,无法一次构造出一个有潜力的解,故不作考虑
(6)
2.2.1 提出的选维方法
在QOL中,维的选择一半采用精英引导选择方法另一半采用随机选择方法。
引导选维首先计算出每维的精英解均值,根据Xi每维与精英解均值的差值,从大到小选择要改进维数。使用精英解可以预测一个当前最有潜力的进化区域。在一个解中,若其中一维偏离预测的区域越远,那该维相对于其它维改进的成功率就越高。使用引导选维选出改进成功率较高的维则可加快解的改进速度。
剩下的维采用随机选择方法。随机选维一方面是为了让所有的维都有机会参与到QOL中,另一方面也可以避免精英解引导选维陷入特例中,不失一般性。
2.2.2 QOL的具体流程
QOL的具体流程可描述为以下9个步骤。
步骤1使用式(6)计算要改进的维数n。其中p=4;
步骤2产生Lm(2n)正交表(OA),其中m=n+1;
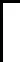
步骤4对选中的维用式(7)构造Ti;
步骤5根据OA和选中的维,通过从Ti或Xi中选择相应的值,构成m个测试解Zj(j= 1,…,m);
步骤6依次评估测试解Zj,并记录最佳解Zbest;
步骤7计算每个水平对因素的影响,并确定每个选中因素的最佳水平;
步骤8根据步骤7中确定的最佳水平构造预测解Zpre,并评估Zpre;
步骤9将f(Zbest)与f(Zpre)进行比较,并将更好的解代替原解Xi
Ti=Xk+ rand(0,1)(Xbest-Xk)
(7)
式(7)用于生成一个解Ti与随机选择的Xk共同参与到QOL中,其中rand(0,1)为[0,1]之间的随机数,k∈{1,2,…,SN}且k≠i,Xbest是当前种群中的最优个体。
2.3 QOABC算法流程
将QOL方法嵌入到ABC算法中形成了QOABC算法。完整的伪代码如下所示。与ABC算法相比,在每次循环的最后隔代启动QOL((42)~(44))。
(1)初始化参数,SN=NP/2,limit=SN*D,max_FEs=5000*D,gap=0.6
(2)iter=0;top=0.25;
(3)通过式(1)初始化种群
(4)评估每个个体,设置FEs=SN,trial[i]=0;
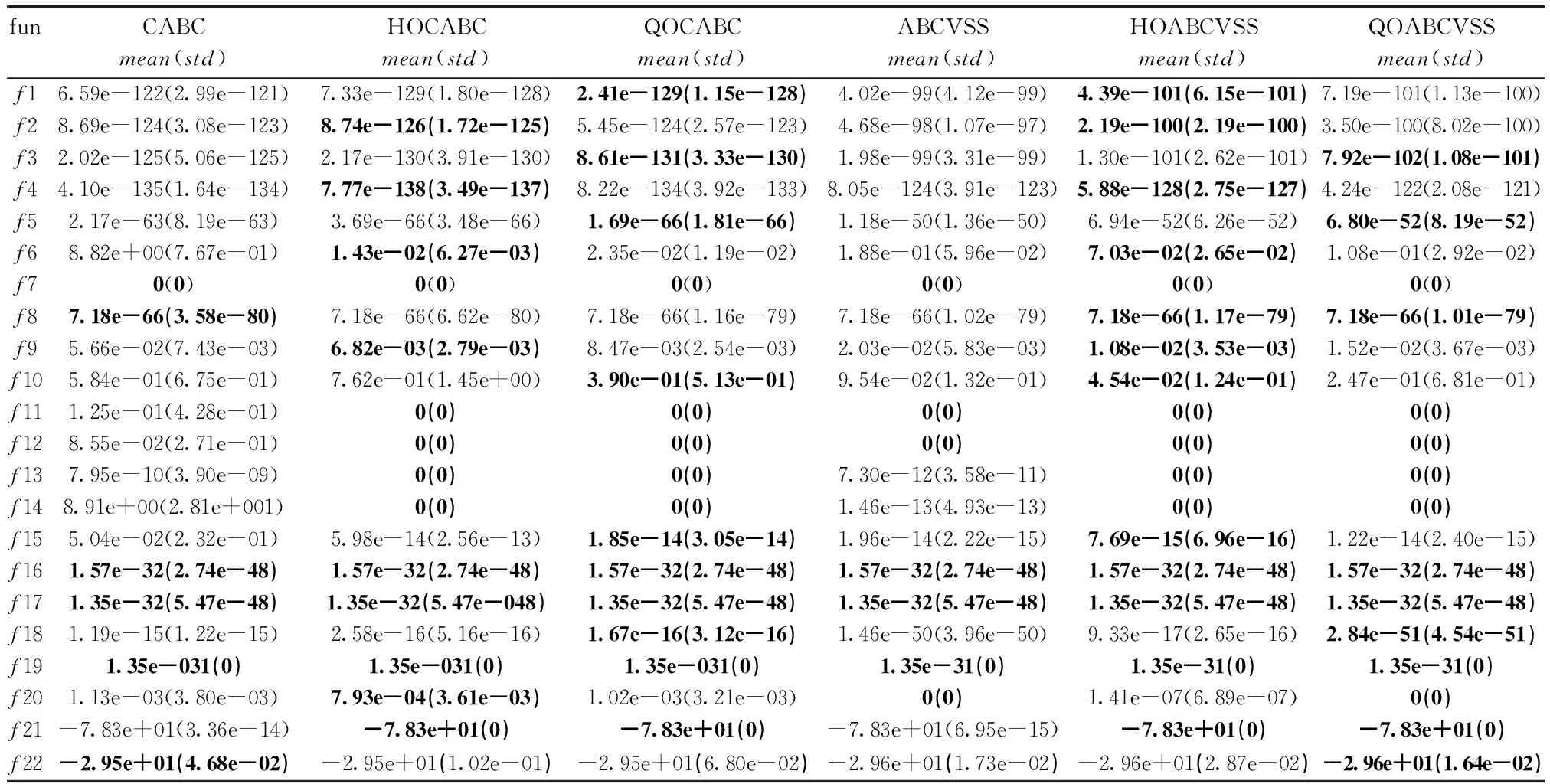
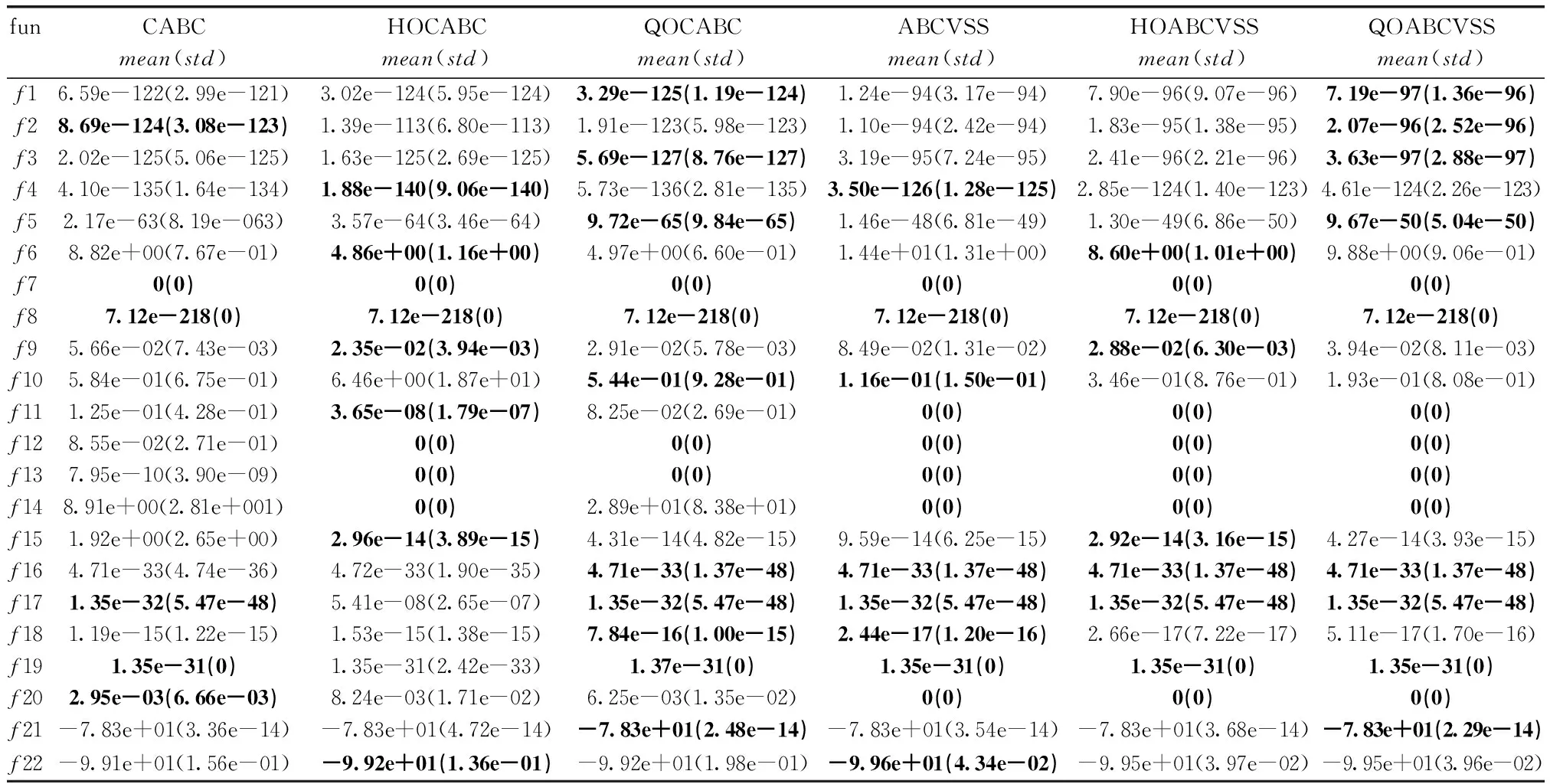
(5)while(FEs (6)fori=1∶SN▶雇佣蜂阶段 (7) 使用式(3)为Xi生成一个新的候选解Vi (8)iff(Vi) (9)Xi=Vi;trial[i]=0; (10)else (11)trial[i]=trial[i]+1; (12)endif (13)FEs=FEs+1. (14)ifFEs>=max_FEsorf(Xi)<=Acceptthen (15) 记录目前为止找到的最优解 (16) 跳出最外层的while循环 (17)endif (18)endfor (19) 使用式(4)计算pi▶观察蜂阶段 (20) 根据适应值的排名,选出最优解和精英解(T=top*SN) (21)fort=1:SN (22) 根据pi轮盘赌选择i (23) 使用式(3)为Xi生成一个新的候选解Vi (24)iff(Vi) (25)Xi=Vi;trial[i]=0; (26)else (27)trial[i]=trial[i]+1; (28)endif (29)FEs=FEs+1. (30) ifFEs>=max_FEsorf(Xi)<=Acceptthen (31) 记录目前为止找到的最优解 (32) 跳出最外层的while循环 (33)endif (34)endfor (35) 更新全局最优解 (36) 找出trail值最大的解Xmax▶观察蜂阶段 (37)if(trial[max] >limit)then (38) 通过式(1)重置 (39)FEs=FEs+ 1,trial[max]=0; (40)endif (41)iter=iter+1; (42)ifiter%(gap*D)==0then ▶QOL阶段 (43) 随机选择一个个体Xi启动QOL操作 (44)endif (45)endwhile 本文使用了一组22个可扩展的基准函数[4],见表1。其中,f1~f6和f8是连续的单峰函数;f7是不连续的阶跃函数;f9是一个噪声4次函数。f10对于D=2和D=3是单峰的,而当D>3时它可能有多个最优解。f11~f22是多峰函数。当算法在运行中获得的最佳解的目标函数值小于接受值时,作为一个成功的运行。为了公平比较,所有算法的参数均与原文相同。其中max_FEs=5000*D,SN=40,limit=SN·D。对于嵌入HOL和QOL的所有算法,gap都设置为0.6。 表1 测试函数集 在本文对原算法和新算法的评估中使用了3个指标,均值与标准差,平均函数评价次数和成功率。 均值与标准差(mean,std)用来测试求解的精度,均值和标准差越小说明求解越精确且越稳定。 成功率(SR)用于测试算法的鲁棒性。SR越大算法的鲁棒性越强。 平均函数评价次数(FEs)为算法找到可接受解时使用的评价次数,用于测试收敛速度。FEs越小即收敛速度越快。 本文在均值和标准差的测试中所有的算法对每个测试函数进行25次独立运行。在成功率与评价次数的测试中所有的算法对每个测试函数进行50次独立运行。 3.2.1 均值与标准差的汇总对比 为了分析HOL和QOL的性能,本节把HOL和QOL方法嵌入到两种ABC算法中(CABC和ABCVSS[13]),分别生成了HOCABC、HOABCVSS、QOCABC、QOABCVSS。并把新算法与原算法在D=30和D=100上进行比较。结果见表2、表3,加粗字体为最优解。 表2 D=30均值与标准差比较结果 表3 D=100均值与标准差比较结果 表2为D=30上的实验结果。对表中的均值和标准差的最优解的个数统计得,CABC、HOCABC和QOCABC分别在6,14,15个函数上表现最优,ABCVSS,HOABCVSS和QOABCVSS分别在7,16,15个函数上表现最优。 表3为D=100上的实验结果。对表中的均值和标准差的最优解的个数统计得,CABC,HOCABC和QOCABC分别在6,11,13个函数上表现最优,ABCVSS,HOABCVSS和QOABCVSS分别在14,13,15个函数上表现最优。 综上所述,ABC算法中嵌入HOL和QOL方法,可以在解的质量上有效地提升算法的性能,且嵌入QOL的算法表现最佳。 3.2.2 加速比与成功率的汇总对比 为了直观比较,本文计算出SP和ARSP,并将每组22个函数的SR和ARSP汇总取平均值,其结果见表4、表5。 表4 D=30 SR与SP加速比比较结果 表5 D=100 SR与SP加速比比较结果 (1)成功表现(SP),由于一些算法可能无法在每个测试函数上成功地找到可接受的解,在这些问题上SP能直观评估收敛速度。SP越小代表收敛速度越快。成功表现的计算公式为SP=mean(FEsfor successful runs)/SR。 (2)SP加速比(ARSP),用于比较算法性能,如公式所示,ARSP越小代表算法性能越好。ARSP的计算公式为ARSP(QOABC)=SP(QOABC)/SP(ABC)。 如表4、表5所示,CABC嵌入HOL和QOL后在D=30上ARSP有5%以上提升,在D=100上ARSP有10%以上提升,ABCVSS嵌入HOL和QOL后在D=30和D=100上ARSP均有5%以上提升。CABC和ABCVSS嵌入HOL后,在D=30上SR分别下降了0.73%和0.09%,在D=100上SR分别提升2.45%和1.09%。CABC和ABCVSS嵌入QOL后在D=30和D=100上SR分别提升了0.23%,0.63%,3.18%和1.64%。这说明嵌入QOL和HOL的算法在开发能力上都有显著提升,但是嵌入QOL的算法鲁棒性更好。 本文提出了QOL方法,通过使用相同评价次数可以修改的最大维数参与正交学习。为了选出参与QOL的维,本文提出了精英引导与随机相结合的选维方法。通过精英解预测优质区域,选出进化较落后的维,使其有更多被选中的机会,增强了开发能力。同时保留随机选维保证了每个维都有被选中的机会,保持了探索能力。通过实验测试,嵌入QOL的算法在几乎所有函数上求解精度,收敛速度和鲁棒性都有显著提升。后续工作将把QOL的思路应用到其它进化算法中,例如PSO、DE等,以及解决多目标优化问题中。2.4 时间复杂度分析
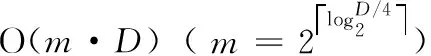
3 实验与分析
3.1 测试函数集和参数设置

3.2 实验数据对比


4 结束语
