基于智能手机的室内外行人定位算法

李冬阳，赵忠华，晏懿琳，卢 菁

(上海交通大学 电子信息与电气工程学院 仪器科学与工程系，上海 200240)

0 引 言

在室内外的环境下，惯性导航系统[1](inertia navigation system，INS)可以克服全球卫星定位系统(global navigation satellite system，GNSS)信号失效的困难。随着手机传感器精度的提高，使用手机进行简单便捷的导航定位也逐渐成为了研究热点。

行人惯性导航的传统方法是将惯性测量单元模块固定在足部，通过对陀螺仪输出角速度的积分获得姿态信息，利用姿态对加速度二次积分得到位置信息。由于MEMS(micro electro mechanical system)陀螺仪具有零偏和漂移，使得到的航向角出现不可避免的误差，而且误差会随时间推移累积。文献[2]提出了启发式漂移减少的技术，将航向误差降低了近一个数量级。但是这种方法无法修正曲线运动的航向角。文献[3]利用滑动窗口的方法用三轴磁力计来实时修正航向角，在噪声环境显示出良好的性能。但是磁力计容易受环境影响，从而降低导航定位稳定性。文献[4]将地图信息作为辅助，在40 min的步行过程中解算出优于5 m的位置精度，但该方法依赖于地图信息辅助，适用范围较窄。为使用智能手机这种便捷的设备在室内外都提供较好的定位精度，提出了一种航向修正的方式，利用上一零速时刻的航向角与下一动态时刻航向角的差值作为观测来修正航向角，设计在室内的外磁干扰检测算法，在较强的磁干扰下选择使用陀螺仪航向角。使用Java语言在Android Studio上开发手机传感器采集应用来采集传感器变化值，然后将数据拷贝到PC端使用Matlab进行计算。通过实验验证，对航向修正和高程修正有一定的效果。

1 行人导航系统原理

用微惯性测量单元来做行人导航系统的方案有两种：SINS算法和PDR算法。后者主要步骤是步长估计和方向估计，通过将步长投影到前进方向的二位平面上，不能获得三维的空间信息，适用场景有限。捷联惯性导航系统可以获得的三维的位置信息和姿态信息，适用场景广泛，但是由于微惯性测量单元传感器精度低，必须在定位期间及时修正，否则速度和位置会发散，导致导航失败。所以行人导航算法的设计是关键技术，本文将微惯性测量单元固联在脚尖，利用行人脚部约0.1 s～0.3 s[5]的静止状态来修正速度，从而修正位移，提高定位精度，整体算法结构如图1所示。

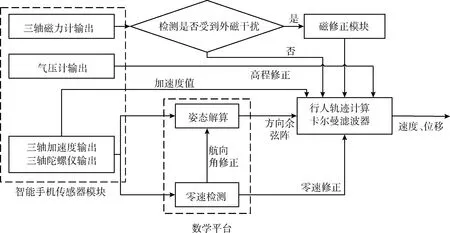
图1 行人导航解算流程

1.1 行人导航解算

指正本文涉及到两种坐标系分别是导航坐标系和载体坐标系：

导航坐标系(n系)：本文的导航坐标系为北-东-地(N-E-D)坐标系。导航系的原点设在载体重心，xn轴与正东方向重合，yn轴与正北方向重合，zn轴符合右手正交定则。

载体坐标系(b系)：本文载体坐标系定义为前-右-下，原点位于载体重心，xb轴与载体纵轴方向重合，yb轴与载体横轴方向重合，zb轴符合右手正交定则。

行人导航系统解算可以分为4个部分：

(1)利用加速计、陀螺仪和磁力计的输出解算出方向余弦矩阵，是转换坐标系的基础；

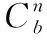
(1)

(2)

(4)得到导航坐标系的速度的基础上，积分得到导航系的位移，如式(3)所示。在积分之前根据零速检测结果对速度进行修正，否则结果误差很大

(3)

按照上述公式直接解算会得到较大的误差，所以对误差模型分析和建立。

1.2 行人导航误差

行人导航系统算法是在理想条件基础上建立，而实际情况中有多种多样的误差。误差的主要来源有：传感器初始的安装误差、传感器本身精度不高带来的误差、一些在期望之外的干扰运动所产生的误差以及数据解算的近似误差。所以对导航误差模型的准确建立十分重要，下面对系统的姿态、速度、位置进行误差建模[6]。

姿态误差

(4)

在零速时刻，ωin=ωie，δωin=0；忽略安装误差和刻度系数造成的误差，不考虑右边第一项，将上式化简为

(5)

其中，εn为导航系的等效陀螺漂移，包含白噪声，一阶马尔可夫还有随机常值，在零速修正过程可以通过卡尔曼滤波对其估计。

速度误差方程

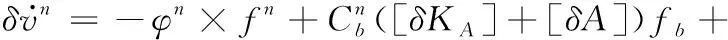
(6)

在零速时刻，vn=0，ωen=0，不考虑刻度误差和安装误差，上式可简化为

(7)

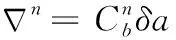
位置误差方程

(8)

在零速时刻，ωen=0，所以上式简化为

(9)

对姿态、速度、位置的误差模型建立之后，将误差模型整理到卡尔曼滤波模型里，然后对导航参数进行修正，在第四节中详细介绍卡尔曼滤波模型。

2 零速检测

如果只按照上述导航方程解算位置，将会有很大的误差，造成导航定位失败，所以要利用行人行走的规律来修正位置。当人在行走的过程中，一只脚处于摆动状态，而另一只脚有短暂的静止状态。正是有大约0.1 s～0.3 s的静止状态，可以用来修正速度，将误差反馈到观测器中。主要的方法分为两类，一类是借助外部传感器来检测，一类是利用自身的加速度计和陀螺仪来判断。文献[7]用传统的加速度模值和加速度滑动方差来进行零速检测，具有一定的可行性。文献[8,9]使用了SVM和马尔可夫模型将零速区间分为几个部分，取得了较好的结果。文献[10]提出了自适应阈值的零速检测算法，以适应行人不同的运动状态，使零速检测率达99%。

本文使用了多条件判定算法，同时使用加速度计和陀螺仪实现零速检测，给加速度和角速度加一个窗口为15的中值滤波，使噪声平滑，提高检测算法精度。

3个条件分别为C1，C2，C3：

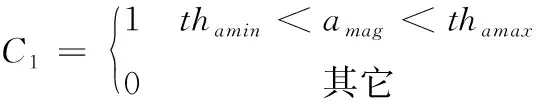
(10)

(2)在零速区间内加速度和处于重力加速度附近，所以加速度矢量和方差值在该区域趋于零，而在动态区域较大

(11)

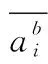
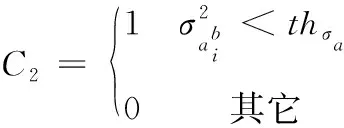
(12)

(3)在零速区域内角速度矢量和趋于0,根据经验设置上限thωmax=1.2 rad/s

(13)

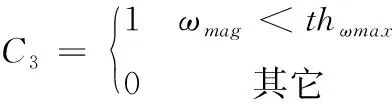
(14)

前3个条件得到的判定结果都略大于实际的零速区间，否则取交集之后零速区间会过小，导致速度发散，导航失效。取3个条件的交集之后得到图2中最下面的判定曲线，和加速度模值基本吻合，验证判定结果较好。

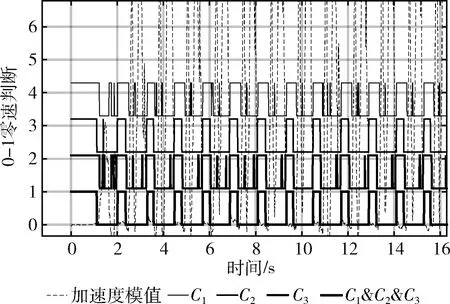
图2 零速检测结果

3 室内外航向修正和高程修正算法

通常在零速状态下可以用ZUPT技术来修正速度和位移，但是航向角误差却无法观测，这将会导致航向角发散，无法完成导航定位任务。同时行人导航系统还伴随着高度发散问题，除了ZUPT技术外，可以通过智能手机的气压计来抑制高度发散。文献[11]提出了启发式航向修正、零角速度修正和磁力计修正的方法。启发式航向修正方法利用行人在相邻两步的航向角差来修正直线运动，设立阈值来判断两步之间是否发生转弯，如果判定为转弯则不补偿，否则就视为直线运动补偿航向误差。但是该方法只能补偿直线运动，对于曲线运动效果有限。磁力计修正的方法依赖于磁力计精度而且易受外界环境干扰，如果在室内导航定位精度会受到较大影响。文献[12]将相邻零速时刻的航向角差值作为观测量，来修正航向角将导航定位精度提高到2%，但是该方法类似于启发式航向修正，如果两个零速时刻之间发生了转向则会有较大的航向差值，导致航向修正发散。本文在这3种方法的基础上提出用上一零速时刻的航向角和下一动态时刻的航向角差值作为观测量来修正航向角，在曲线运动中取得了良好的效果。在室内环境有不同大小和方向的外磁干扰，如果只使用纯地磁航向角来修正航向角会不可避免地使航向产生误差，影响导航定位精度。将受到较大磁干扰的区间检测出来，在这个区间内使用陀螺仪航向角代替磁航向角，使算法在室内也能表现良好。利用手机中的气压计来抑制高度发散，这将在长时间导航任务中发挥着重要作用。

3.1 传统航向修正

(1)启发式航向修正

当行人按直线或接近直线的线路行走时，相邻两步的航向角变化是非常小的。行人进行曲线行走时，当前这步的航向角相对于前一步的航向角会发生较大变化，因此可以利用相邻步之间航向角的突变来检测行人的曲线运动。为了保证转向检测的正确率，本文采用3个相邻步间的航向变化来检测曲线运动，如式(15)所示

(15)

式中：m表示行走路线状态，1代表直线，0代表转弯；φk表示当前步的航向角，φk-1和φk-2分别表示前一步和前两步的航向角，φth表示偏差阈值。通常情况下，设定角度值8°作为阈值。当判断行人走直线时，计算当前航向角与上一时刻航向角的差值，将差值补偿到下一个航向值,此处航向角选取静态的第一个点

(16)

(2)零角速率修正

当检测到零速区间时，真实速度和角速度都为0。零速时刻陀螺仪输出的角速度值为偏差，可以用来修正角速度，如式(17)所示，从而能修正航向角来提高姿态解算精度

(17)

(3)磁力计融合

本文所使用的IMU传感器中包含磁力计，可以用磁力计输出值来修正航向角。磁力计是一种无源器件，通过测量地球的磁场强度，可以得到载体的绝对航向角。不同环境对磁力计的准确度影响较大，尤其是室内。每次在室内使用前要先修正，从而得到更准确的读数。

(18)

可以计算出航向角

(19)

其中，φ0为磁偏角，可以通过表查得。

3.2 利用零速时刻的航向角作为动态的观测

通常，解算出的航向角在零速时刻比较稳定，而在动态时上下波动较大，因为积分出的速度和位置信息也处在动态时刻，只利用到了动态时刻的航向角。在之前的研究者们的工作中，很少有利用零速时刻比较稳定的航向角，文献[12]中利用了相邻零速时刻的航向角差值作为观测量来修正航向，该方法更适用于直线运动中，作者的实验路线选择了长方形。然而实际情况中曲线和直线运动混杂，所以本文在ZIHR(zero integrated heading rate)修正方法的基础上提出一种航向修正方法，适用在直线和曲线运动，利用上一时刻零速区间的航向角和下一动态时刻航向角的差值作为观测量，从而来修正航向的漂移，通过实验验证提高行人导航定位的精度。

载体坐标系相对于导航坐标系的旋转角速度向量ωnb为

(20)

将旋转角速率分解到载体坐标系上

(21)

展开成矩阵形式为

(22)

对上式求逆可得

(23)

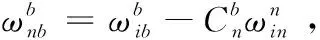
(24)

(25)

(26)

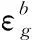
(27)

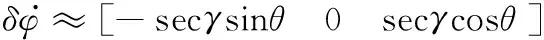
(28)

将航向角整理到观测方程中

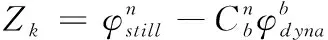
(29)

将上式整合到观测矩阵里为

航向角可观测性分析：对于脚绑式行人惯性导航系统，航向角在静态时比较稳定，而在动态时航向角变化较大。按照大多数人的行走习惯，行人在静态时候的航向也是下一时刻踢脚的方向。当IMU在静态时，由于没有动态误差，解算出来的航向角的误差也更小，利用在静态时的航向信息来修正下一时刻的动态航向角，提高行人导航定位精度。

3.3 检测磁力计是否受到外磁干扰

对于室外空旷的地方，磁力计能提供持续稳定的航向信息，然而室内容易受到磁干扰，会严重影响到解算结果。为了解决这个问题，在文献[13]中提出地磁航向角与陀螺仪航向角差值的阈值条件，检测是否受到硬磁场的干扰。但是这种检测外磁干扰的方法过于单一，假如陀螺仪航向角解算误差过大导致系统错误检测了外磁干扰区间。所以在此方法基础上再使用磁力计模值阈值条件和磁力计模值方差检测条件共同判断受外磁干扰的区间

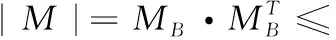
(30)

式中：ξM为行走前静止状态磁力计模值均值，m为方差窗口大小，ξgc为磁航向角与陀螺仪航向角差值阈值。同时满足上式，说明磁力计在此刻受到外磁干扰，此时磁力计提供稳定可靠的航向角。如图3所示，磁力计测量值模值局部变化较为剧烈，但是整体来看是一个缓变量，行走到不同的室内环境就会受到不同大小的外磁干扰。图3是磁力计在零速时刻的模值，将动态时刻磁力计置为0。在15 s～17 s，84 s～86 s等区间检测到磁力计受到外磁干扰，大幅度超出稳定时的磁力计测量模值，如圆圈所示。此时使用陀螺仪航向角来代替地磁航向角，以免解算结果漂移。

图3 磁力计在零速时刻的模值变化

3.4 利用气压计修正高程误差

由于解算轨迹在高度方向难免会产生发散问题，使得行人导航系统随着时间而发散，除了零速修正之外，需要引入气压计作为高度观测值来修正高程误差。在0 m～20 000 m 之间有两个高度层，即对流层和同温层，对流层的海拔范围为0 m～11 000 m，同温层的海拔范围为11 000 m～20 000 m。由于本文实验场地约为5 m左右，属于同温层，标准气压高度公式为

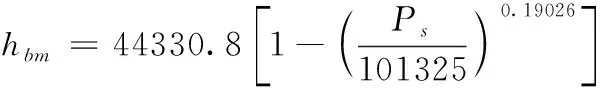
(31)

式中：hbm为气压计测量高度，hs为捷联惯导求得的高度信息，Ps为气压计测量值。

将上式整合到观测矩阵里为

经过气压计的高程修正，较好抑制住了高程误差。

4 行人导航系统自适应卡尔曼滤波模型

经过上文的分析，将误差模型、零速修正和航向修正公式整理到自适应卡尔曼滤波中。当检测到零速区间时，将这个区间的速度置零，利用速度误差修正动态时刻速度，利用上一零速时刻航向角与下一动态时刻的航向角差值来修正航向角。状态方程由误差模型方程组成，分别是姿态误差、速度误差、位置误差、陀螺偏移误差、加速度偏移误差，观测模型由ZUPT、航向修正和气压计修正组成。使用自适应滤波对系统和观测噪声进行估计和修正，增强行人定位算法的适应性。

系统的状态变量为

(32)

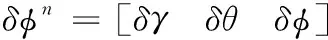
系统的观测方程为

δZk=Hδxk+vk

(33)

其中，δZk是时间k的误差测量值，H是测量矩阵，vk是测量噪声。

观测方程由3部分组成，第一部分是零速区间末的速度值，来修正动态时刻的速度；第二部分是上一零速时刻航向角与下一时刻动态时刻航向角的差值，作为观测量来修正动态时刻的航向角；第三部分是利用气压计测量的高度来修正行人轨迹的高程误差。

(1)将状态方程和观测方程离散化

δXk+1=AkδXk+WkδZk=HXk+Vk

(34)

状态转移矩阵

其中，τg和τa分别是陀螺仪和加速度计的相关时间，Δt代表采样时间间隔，fn×是导航系中的各加速度构成的偏斜对称矩阵。当检测到零速区间时，用零速区间上一时刻的速度减零即为速度误差，然后将速度误差输入卡尔曼滤波器进行观测更新,利用上一零速时刻航向角与下一动态时刻航向角的差值作为观测量，来修正航向角。

对于基于ZUPT和航向修正的卡尔曼滤波器，测量矩阵H的表达式如下

(2)预测及观测量

状态单步预测为

(35)

单步预测误差协方差为

(36)

(3)求速度、航向角和高程的零偏估计

状态估计

(37)

误差协方差更新

(38)

滤波增益更新

(39)

(4)计算加权系数并更新相关参数

(40)

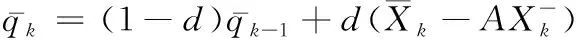
(41)

在导航参数修正完成后，由于δφn、δVn和δPn不属于零偏误差，该误差已经在这次修正阶段修正完成，所以要将这些参数置0。

5 实验与结果分析

为了检验本文行人导航系统的准确性，验证航向修正和高程修正算法的可行性，分别设计了室内外3组行人轨迹实验。

实验一的场地在上海交通大学南体体育场，自西南角足球场角球位置为起点，逆时针方向，沿规则足球场边线行走一圈。

实验二的实验场地在上海交通大学南体体育场，自西南角100 m跑道终点为起点，逆时针方向，沿400 m跑道第一赛道行走一圈。

实验三的实验场地在上海交通大学电子信息与电气工程学院2号楼与3号楼之间的二楼走廊，顺时针行走一圈。

5.1 实验条件及数据采集

本文使用的传感器数据均来源于华为Mate9，使用Java语言在Android Studio上开发传感器数据采集app，将传感器采集频率参数设置为SENSOR_DELAY_FASTEST，频率最高可到500 Hz。通过时间戳来控制采样周期，每个采样周期存储一次传感器数据从而精准控制采样频率。实验中将手机固定在行人右脚脚踝，如图4所示，实验结束后点击保存按钮存储各传感器数据，最后将数据拷贝到PC端使用Matlab进行计算。

图4 载体坐标系

采集数据的传感器包括三轴陀螺仪、三轴加速度计、三轴磁力计和气压计，符合实验的要求。表1是智能手机各传感器技术指标。lsm6 dsm是三轴加速度计和三轴陀螺仪合二为一的传感器，磁力计是akm09918，气压计是airpress_lps22bh。

表1 Mate9各传感器指标

5.2 实验结果和分析

实验设计共分为两类，分别是室外曲线和室内曲线。室外实验分别是直线闭合曲线和直线曲线混合曲线，设置直线路径和曲线路径对照，对比使用与未使用该航向修正算法之间的差别和关系。由于室外操场的实验磁力计不易受到外磁干扰，可以不使用检测外磁干扰模块。

实验一：图5为操场的标准足球场边线，长105 m宽68 m，总长346 m。从西南角角球位置开始(图中圆点)逆时针沿着边线行走一圈，只用ZUPT约束解算的定位误差为34.5 m，误差为8.62%,结合ZUPT与航向修正算法之后解算的定位误差为2.64 m，误差为0.76%。较好限制了航向角的漂移。利用气压计来修正高程误差，将高程误差限制在0.3%以内。

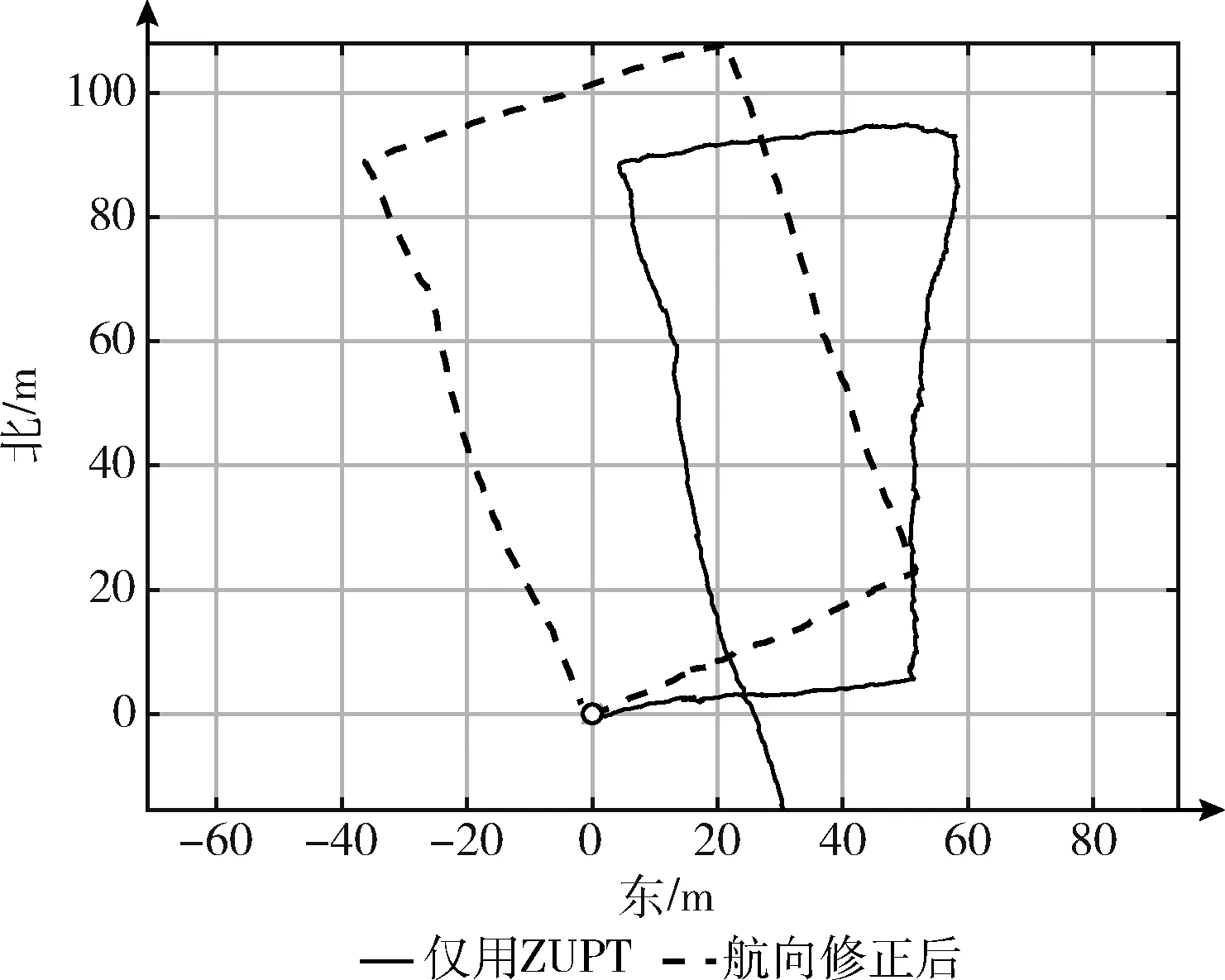
图5 标准346 m足球场边线行走

实验二：图6为操场的400 m的跑道内道，从西南角(图中圆点)出发逆时针行走一圈，只用ZUPT约束解算的定位误差为38.6 m，误差为9.7%,结合ZUPT与该航向修正算法之后解算的定位误差为2.9 m，误差为0.72%。较好限制了航向角的漂移。利用气压计来修正高程误差，将高程误差限制在0.4%以内。

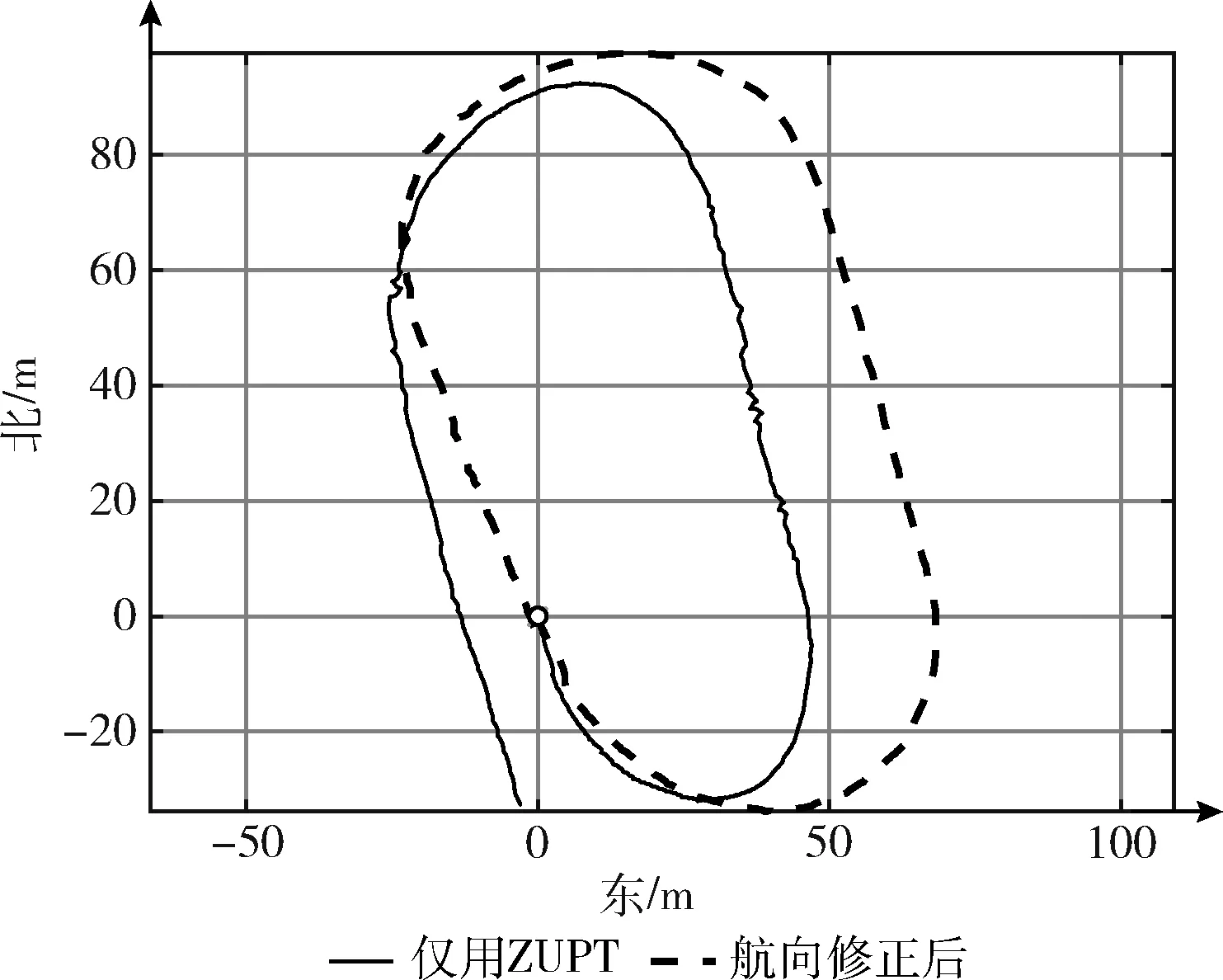
图6 操场400 m闭合路径行走

实验三：图7为上海交通大学电子信息与电气工程学院2号楼与3号楼之间的二楼办公室过道和走廊，从2号楼西侧楼梯口为起点顺时针行走一圈，只用ZUPT约束解算的定位误差为46.7 m，误差为15.3%,结合ZUPT与该航向修正算法之后解算的定位误差为14.4 m，误差为4.8%，较好限制了航向角的漂移。但是还存在一些外磁干扰点，经过外磁干扰检测模块后，对修正航向有一定的帮助，定位误差为3.5 m，使定位误差小于1.2%。利用气压计来修正高程误差，将高程误差限制在0.3%以内。

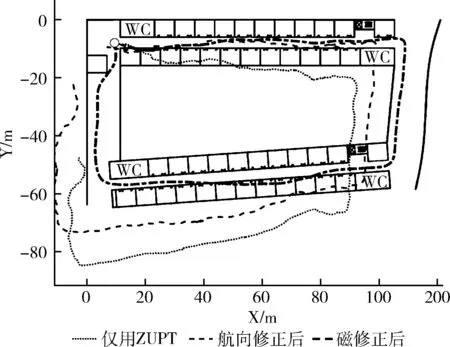
图7 室内路径行走

本文分别设置室内外实验，对仅使用ZUPT、ZUPT+航向修正算法、ZUPT+航向修正算法+磁异常检测修正算法效果进行对比，如图5～图7所示。仅使用ZUPT缺少对陀螺仪的零偏估计，航向角会不断发散，产生较大误差。ZUPT结合航向修正算法可以对航向角误差进行观测，能有效改善解算结果。分别设置直线路径与曲线路径进行对比，验证算法的适应性。但是在室内环境下地磁容易受到磁干扰，不去加以检测和修正同样会使航向角发散。在室内环境下同时使用ZUPT、航向修正算法以及外磁干扰检测修正算法，在室内出现强磁干扰后会检测并暂时放弃使用地磁航向角，以免使航向角发散。从结果来看，基本与实际路线吻合，能够在磁干扰条件下表现稳定。

同时，进行了多组实验验证，并将综合误差统计在表2中。根据数据显示，仅使用ZUPT误差最大，经过航向修正算法后大大降低了室外的误差，在室内通过使用磁异常检测修正后降低了室内行走的误差。

表2 实验误差

6 结束语

本文在零速修正和捷联惯性导航算法的基础上，根据行人的行走习惯：脚在零速时刻的航向和下一时刻踢出的方向是一致的，微惯性器件在静态时解算出的误差更小的性质，提出了一种航向修正的方法，用上一零速时刻的航向角与下一动态时刻航向角的差值作为观测来修正航向，扩充了一维观测器。经过对比实验验证，发现这种方法对航向抑制有效。针对室内存在磁干扰的问题提出了磁干扰检测的方法，较好修正了航向角。本文在一定程度上解决了微惯性陀螺在行人导航系统中航向漂移难以抑制的问题，扩展了适用场景，提高了行人定位精度。