高校突发事件演变机理与应急管理评价

李玉飞， 刘晓云， 刘 洋

（武汉科技大学a.机械自动化学院，b.资源与环境工程学院，武汉 430081）

0 引 言

近年来，我国高校突发事件数量不断增加。高校突发事件具有突发性、扩散性等特点［1-3］，容易对高校和社会造成不良影响，已成为影响高校稳定和发展的重要因素［4-5］。弄清高校突发事件的产生原因、发生条件、演变规律是有效管控高校突发事件的前提和基础，以便为高校管理者科学决策提供参考依据。因此，开展高校突发事件演变机理研究显得尤为重要。

目前，一些专家学者对高校突发事件开展了较多研究。刘效广等［6］采用心理试验，选取高校大学生作为研究对象，探讨了突发事件应急决策中的首因效应，分析了决策者情绪和后果严重性对首因效应的影响；张义庭等［7］基于熵理论，构建了高校突发事件网络舆情模型，阐释了高校网络舆情系统内部的相互作用及影响；吕美等［8］从高校突发事件预警角度出发，构建了高校突发事件预警信息分析模型；皮祖训等［9］基于灰色关联理论，建立了校园安全灰色关联评价模型；张欣［10］结合问卷调查和离散选择模型，分析大学生在校园突发事件中的信息传播行为偏好；杨霞等［11］采用层次分析和专家评分法，构建了高校突发事件应急管理能力的模糊综合评价模型；周荣喜等［12］基于Delphi-AHP和加权集值统计，提出了高校突发事件预警评估方法。

以上专家学者从高校突发事件应急决策、网络舆情管理、预测预警、评价模型构建等不同维度开展了研究，取得了较多研究成果，对高校突发事件应急管理具有重要的指导意义。从非线性数学角度来看，高校突发事件是偏离平衡状态的非线性突变过程，突发性是高校突发事件的主要特征。在高校突发事件应急管理研究中，学者大多将高校突发事件分为事前、事中和事后3 个阶段，但未从高校突发事件本身的非线性、突变性等内在属性出发阐述其阶段划分依据，缺乏一定的理论基础，导致所采取的应急管理方案实效性不强，需要进一步弄清高校突发事件的演变过程，进而提出有针对性的应急管理对策。

突变理论是研究不连续现象的新兴科学，根据突变模型的势函数，可分析临界点附近非连续状态的特征，展现系统在连续性的变化中突然中断，引起质变的过程，进而分析出现的突变现象。目前，突变理论已应用到危化品道路运输系统安全评价［13］、长三角生态安全评价与预警［14］、害虫种群动态模型［15］、风电场群静态电压稳定性分析［16］，涉及社会科学、生物科学、物理科学等诸多领域，以上应用证明了突变理论具有较好的适用性。基于此，采用突变理论，分析高校突发事件的突变特征，阐释高校突发事件的非线性演变机理。在突变理论的基础上，构建高校突发事件应急管理评价的突变级数模型，并结合实例进行说明。

1 高校突发事件的突变特征

当研究对象的系统参数变化时，突变模型势函数描述的系统具有多平衡位置、跳跃性、滞后性、不可达性等突变指征，可以解释系统中出现的不连续状态。高校突发事件具有明显的突变特征［17-18］，因此可以采用突变模型分析高校突发事件的突变特征。

在初等突变模型中，尖点突变模型临界曲面容易构造，且几何直观性强，应用最为广泛，因此选用尖点突变模型。尖点突变模型的平衡曲面如图1 所示。

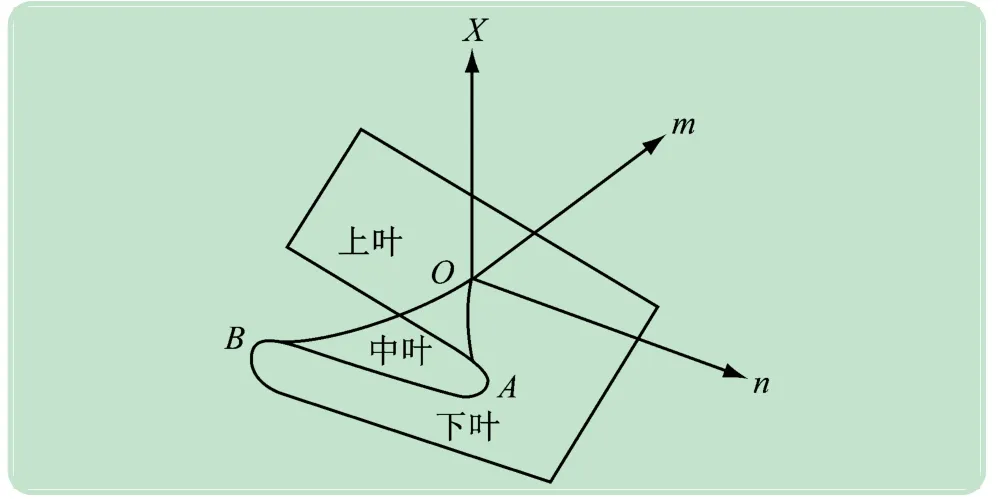
图1 尖点突变模型的平衡曲面

（1）多平衡位置。从图1 中知，位于中叶的势函数取极大值，系统的平衡位置具有不稳定性，位于上叶和下叶的平衡位置是稳定的。当高校发生突发事件时，系统处于不稳定状态；未发生突发事件时，系统将保持稳定平衡状态，此时系统势函数对于控制参数的某些范围内可能有2 个或多于2 个的极小值。

（2）跳跃性。外界条件发生变化时，将导致系统状态发生变化。在图1 中，当系统的平衡位置在上叶时，在外在因素的影响下，平衡位置将突跃到下叶。高校内某一外部因素的变化可能导致突变事件的突然发生，系统状态将由原来的稳定平衡状态转向不稳定状态，即发生突发事件。

（3）滞后性。当物理过程并非严格可逆时，会出现滞后性，而突变过程具有不可逆的特征。高校突发事件的发生具有突发性，高校管理者在人员伤亡、影响范围等方面的信息获取需要一定的时间，使得在判断决策上出现一定的滞后性，需要建立和完善高校应急管理快速反应机制。

（4）不可达性。图1 中由不稳定稳态点组成的区域穿插在定态稳定点之间，这些点是不能实现的定态点。高校突发事件的发生受内部、外部等多种因素的影响，只有达到突发事件的条件时，才会发生突发事件。因此，在高校突发事件应急管理中，要重视加强突发事件影响因素管控，查漏补缺。

2 高校突发事件的演变机理

2.1 双尖点突变模型

由突变理论知，双尖点突变模型可以解释非线性系统失稳的突变过程，为此将高校视为一个整体系统，建立系统动力学方程和势函数，构建高校突发事件的双尖点突变模型，阐释高校突发事件的动态演变机理，分析高校从安全状态演变为突发事件状态的过程。

双尖点突变模型的标准平衡曲面方程为：

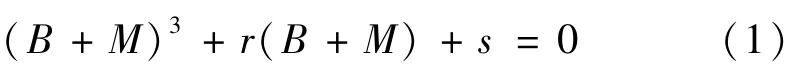
式中，r、s为控制变量，B ＋M 为状态变量，可将状态变量看作由B 和M两个变量组成，式（1）可视为由两个尖点突变模型构成的双尖点突变模型，如图2 所示。

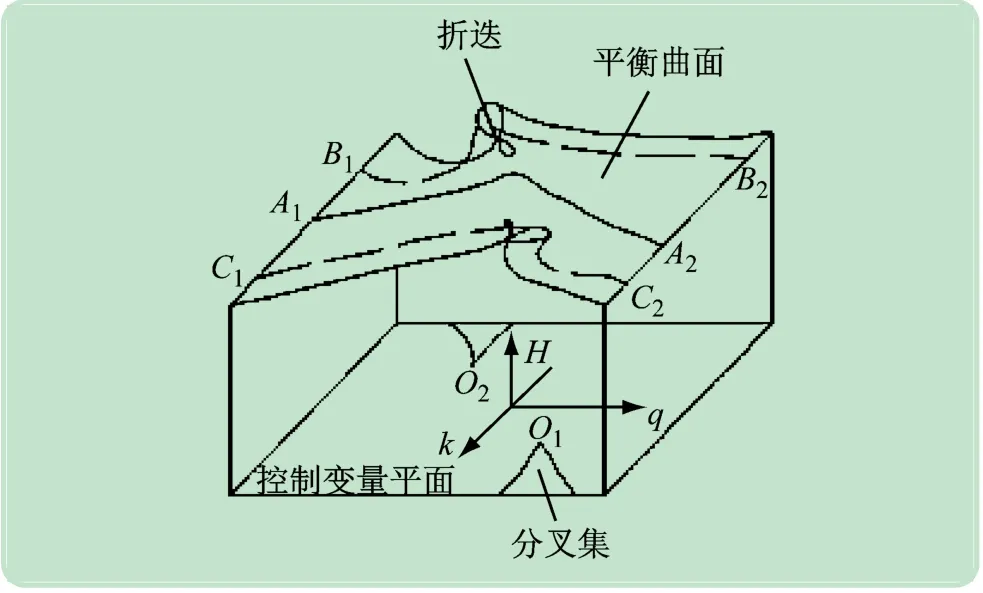
图2 双尖点突变模型

2.2 非线性演变机理

将图2 中两个位于分叉集尖角处的尖点位置坐标分别设为O1（f1，k1）和O2（f2，k2）。k 值的不同对高校是否发生突发事件具有不同的响应，这里可以把f 值看作系统发生突发事件的内在因素，把k 值看作外界条件的集合，将k值分为k2＜k ＜k1、0 ＜k ＜k2、k ＞k13种情形，系统在控制变量平面上的投影如图3-5 所示，分别与图2 中A1A2、B1B2、C1C2曲线对应。

当k2＜k ＜k1时，从图3 可以看出，系统随着f 值的变化而连续变化，系统呈现近乎线性的趋势，此时系统不会发生失稳，即高校不发生突发事件。

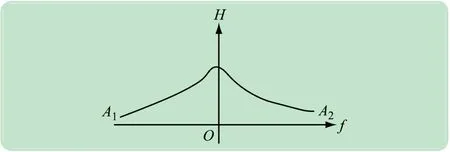
图3 k2 ＜k ＜k1 时在控制变量平面上的投影图

当0 ＜k ＜k2时，在图4 中，从左向右分析f 值时，可将系统失稳过程分为曲线B1a1阶段、a1b1阶段和b2B2阶段，进而分析高校突发事件的演变机理。在曲线B1a1阶段，系统出现连续变化，此时高校不会发生突发事件；在曲线a1b1阶段，当f 值增大到某一量值，系统发生突跃，高校从安全状态演化为突发事件状态，该阶段验证了高校突发事件是一种非线性的突变过程；在曲线b2B2阶段，f值继续增大，系统呈线性变化，表明高校突发事件已经结束，高校重新恢复到稳定状态。当从右向左分析f 值时，分析过程与从左向右分析f值相同。由此可知f值不同，导致高校突发事件的演变路径也不同。

图4 0 ＜k ＜k2 时在控制变量平面上的投影图

当k ＞k1时，从图5 可以看出，系统发生突发事件的演化规律与0 ＜k ＜k2时类似，不同的是系统发生突跃的f值不同。

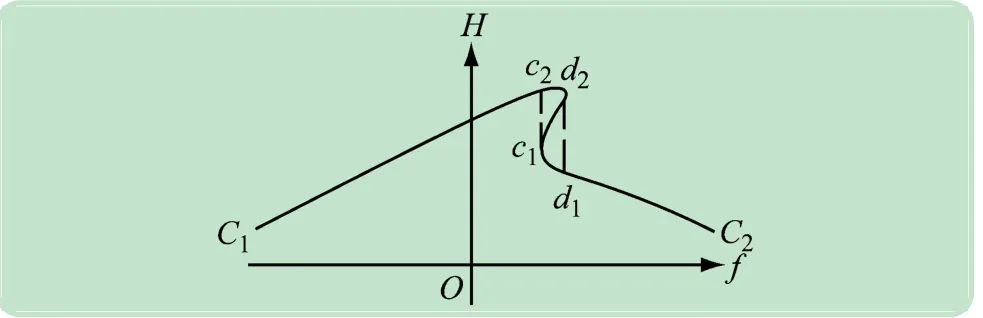
图5 k1 ＜k时在控制变量平面上的投影图

从以上分析可知，影响高校突发事件的生成因素既包括外界条件的集合k值，也包括内在因素f值，内外因素构成了高校突发事件的充要条件。其中，内在因素f值是高校发生突发事件的根本原因，也是高校发生突发事件的必要条件。

2.3 演化阶段

基于突变理论，采用双尖点突变模型可以阐释高校突发事件非线性系统的失稳过程，证明了突变理论适用于高校突发事件演变机理研究。结合图4，可将系统非线性失稳过程的曲线B1a1阶段、a1b1阶段和b2B2阶段分别定义为稳定量变阶段、失稳质变阶段和稳定恢复阶段。

在稳定量变阶段，该阶段可以看作是高校突发事件的前兆。本阶段若不采取措施，在各种风险的累积叠加效应作用下，高校内部的能量将不断集聚，当总能量积累到一定程度时，会造成平衡状态的势函数发生突变，导致高校发生突发事件。为避免系统从稳定量变阶段转向失稳质变阶段，可对影响系统的外部和内部因素施加作用，阻断内因和外因同时发生作用，防止两者形成合力，阻止或延缓能量的聚集过程。

在失稳质变阶段，该阶段可以看作是高校突发事件的发生过程。为高校减轻突发事件发生的烈度，使损失最小化，应实施应急预案，重点布防，防止事态扩大化；或人为改变系统突变发生的路径，使突变向相对有利的方向发生；或改变造成系统发生突变的内在和外部因素，降低突变过程中的能量强度。由于失稳质变阶段发生时间较短，为高校管理者预留出有效控制的时间有限。因此，在实际情况中，高校要针对不同类型的突发事件加强研判和分析，制定不同的应急预案，定期开展应急演练。

在稳定恢复阶段，该阶段可以看作是高校突发事件的事后管理过程。高校突发事件结束后，系统内部的能量逐步释放，高校恢复到原有的稳定状态。在这一阶段，高校要做好善后处置工作，减轻突发事件造成的损失与影响。同时，高校要对突发事件开展调查分析，完善和优化应急处理措施和应急方案，提高高校应对突发事件的应急储备。

3 高校突发事件的应急管理评价

3.1 应急管理评价指标体系

影响高校突发事件应急管理评价的因素较多，以往高校突发事件应急管理评价指标体系的构建主要基于突发事件的阶段性，侧重于各个阶段的管理。而由高校突发事件演变机理知，高校突发事件的影响因素包括外界条件和内在因素，内在因素是高校突发事件的发生根源，高校突发事件应急管理评价应重点强调内外因素的共同作用。因此，从制度管理、物质保障、精神保障、安全教育、事后改进等方面选取评价指标。在前人研究成果的基础上［19］，遵循评价指标选取的全面性、代表性等原则，选取安全管理规章制度预案、安保人员应急救援等12 个评价指标，并根据评价指标的重要性排序结果，建立高校突发事件应急管理评价指标体系，如表1 所示。

表1 高校突发事件应急管理评价指标体系

参考高校突发事件应急管理分级标准，结合突变级数法计算结果特性，将高校突发事件应急管理等级划分Ⅰ（优）、Ⅱ（良）、Ⅲ（中）、Ⅳ（一般）、Ⅴ（差）共5个等级，Ⅰ级表示达到评价标准的95% ～100%为优，Ⅱ级表示达到评价标准的85% ～95%为良，Ⅲ级表示达到评价标准的75% ～85%为中，Ⅳ级表示达到评价标准的60% ～75%为一般，Ⅴ级表示达到评价标准的0% ～60%为差，高校突发事件应急管理分级划分标准如表2 所示。

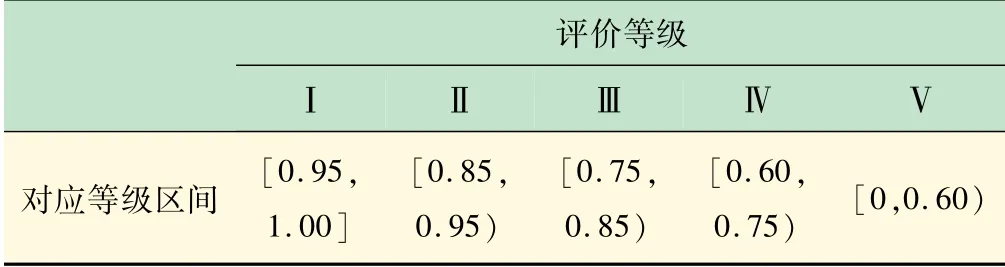
表2 高校突发事件应急管理等级划分标准

3.2 应急管理评价的突变级数模型

突变级数法是突变理论和模糊数学理论相结合的一种评价方法，通过归一化公式，得到各层的突变隶属函数值，进而获得研究对象的突变级数值，实现对评价指标体系的量化分析。根据表3 的突变模型类型和表1 的高校突发事件应急管理评价指标体系，构建高校突发事件应急管理评价的突变级数模型，如图6 所示。

表3 突变模型的常见类型

图6 高校突发事件应急管理评价的突变级数模型

3.3 应急管理分析

由于评价指标为定性指标，较难直接获取，故采取专家打分法确定。选取某一高校，聘请5 位高校突发事件相关研究领域的专家，结合高校实际情况和表2的高校突发事件应急管理等级划分标准与要求，对高校进行打分，专家打分结果如表4 所示。

表4 专家打分结果

根据图6 的高校突发事件应急管理评价的突变级数模型，利用表3 的归一化公式，由无量纲化处理的标准化数据，逐层向上计算各层控制变量的值，即突变隶属函数值，最终计算出A层的突变级数值。计算过程如下：

B1与C1、C2、C3构成燕尾突变模型，则XC1＝（0.92）1/2＝0.949，XC2＝（0.75）1/3＝0.909，XC3＝0。由于控制变量间具有相关性，按照“互补”原则，取平均值，则B1＝average｛0.949，0.909，0｝＝0.619。

B2与C4、C5、C6、C7构成蝴蝶突变模型，则XC4＝（0.83）1/2＝0.911，XC5＝（0.17）1/3＝0.554，XC6＝（0.83）1/4＝0.954，XC7＝1.000。由于控制变量间无相关性，按照“非互补”原则，大中取小，则

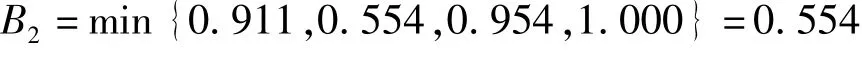
B3与C8、C9、C10构成燕尾突变模型，则XC8＝（0.42）1/2＝0.648，XC9＝（0.50）1/3＝0.794，XC10＝（0.42）1/4＝0.805。按照“互补”原则，则

B4与C11、C12构成尖点突变模型，则XC11＝（0.92）1/2＝0.959，XC12＝（0.75）1/3＝0.909。按照“非互补”原则，则B4＝min｛0.959，0.909｝＝0.909。

A1与B1、B2、B3、B4构成蝴蝶突变模型，则XB1＝（0.619）1/2＝0.787，XB2＝（0.554）1/3＝0.821，XB3＝（0.749）1/4＝0.930，XB4＝（0.909）1/5＝0.984。按照“非互补”原则，则

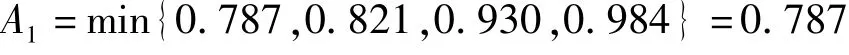
最终计算得到的A 层突变级数值为0.787，根据表2 的高校突发事件应急管理等级划分标准，确定该高校的等级为Ⅲ，这与专家实际调研结果基本一致，验证了将突变级数模型应用于高校突发事件应急管理评价是可行的。

在同一层突变模型中，可计算该层某一评价指标的突变隶属函数值占同层突变模型总突变隶属函数值的比值，比重越大，说明该评价指标的能力越好。相反，比重越小，说明该评价指标的能力越差，需要对能力差的评价指标进行重点管理，进而有效预防高校突发事件的发生。

以蝴蝶突变模型B2和A 为例，由图7 可见，校园精神保障C5在蝴蝶突变模型B2中突变隶属函数值占比最低为16.2%，说明评价指标校园精神保障C5较差，应加校园精神保障能力建设。同理，对于蝴蝶突变模型A而言，应加强安全保障能力建设。

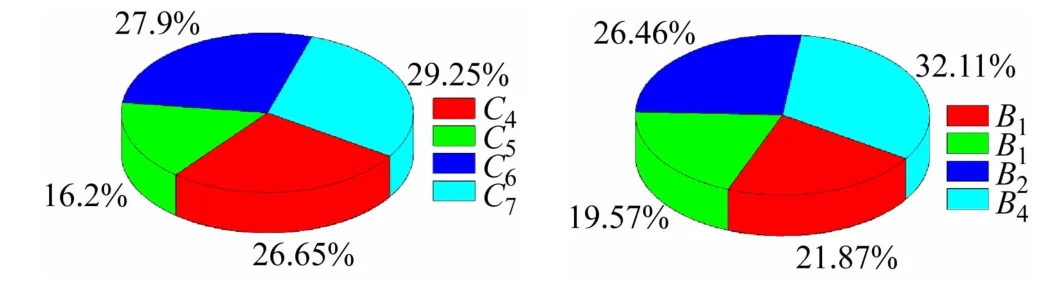
图7 样本中评价指标的突变隶属函数值占比

4 结 语

（1）从非线性的角度出发，采用突变理论分析了高校突发事件的多平衡位置、跳跃性、滞后性、不可达性等特征，这与突变模型势函数描述的突变指征一致，表明利用突变理论分析高校突发事件突变特征具有较好的适用性。

（2）选用双尖点突变模型，采用定性的数学描述，阐释高校突发事件的非线性演化机理，分析高校从安全状态演化为突发事件状态的失稳过程，验证了高校突发事件是一种偏离平衡状态的非线性突变过程，并将高校突发事件非线性失稳过程分为稳定量变阶段、失稳质变阶段和稳定恢复阶段。

（3）将突变理论和模糊数学理论相结合，形成突变级数法，构建了高校突发事件应急管理评价的突变级数模型。通过计算评价指标的突变隶属函数值占同层突变模型的总突变隶属函数值的比值，判断和识别出有待加强的评价指标，为高校突发事件应急管理提供决策依据。

（4）本文着重从理论角度探讨了高校突发事件的非线性演变机理，将高校突发事件的演化过程划分为3 个阶段。下一步，将研究如何在高校突发事件不同阶段中加强外部因素和内在因素管理，提供切实可行的应对方案。同时，将扩充检验样本的数量，对构建的高校突发事件应急管理评价的突变级数模型作进一步验证。

·名人名言·

人不光是靠他生来就拥有一切，而是靠他从学习中所得到的一切来造就自己。

——歌德