实验设备管理绩效动态博弈模型的构建与应用

纪 伦

（哈尔滨工业大学交通科学与工程学院；交通实验中心，哈尔滨 150090）

0 引 言

绩效测评中，指标量化的科学性、合理性是测评体系的焦点，是绩效测评办法的关键。绩效测评的分析方法很多，例如，定性考核有德尔菲专家调查、无领导小组讨论和层次分析法等；定量考核分为因子分析、聚类分析、主成分分析等。以及博弈论、神经网络、多目标决策、模糊模式识别和统计分析等综合方法［1-3］。

而构建绩效测评模型，实现定量分析，可以克服主观因素，使得测评更加科学与准确。基于设备管理绩效测评的特点，本文以实验机构管理岗位人员设备管理绩效测评为例，采用博弈论方法分析博弈属性，构建模型，提出量化分析方法，以便为类似工作提供参考。

1 设备管理绩效测评中的博弈问题

1.1 设备管理绩效测评工作中的博弈状态

（1）管理层级间的博弈状态。高校设备使用绩效测评的过程可以看作高校资产管理部门与实验机构，实验机构与人员之间的博弈过程［4］。从服务国民经济发展，及资源共享角度，学校资产管理部门希望通过延长工作时间、提高服务效率，使设备创造的社会和经济效益最大化；而实验机构或人员，出于使用目的考虑，设备使用能满足其自身教学或科研目标即可，出于资源垄断、技术封锁或懒散态度，不愿意承揽委托实验，而增大工作量。由于二者的目标差异，设备绩效测评中出现博弈状态。类似的，在一定的环境下，实验机构与其管理工作人员也存在同样的博弈关系［5～7］。

（2）绩效测评体系中的博弈状态。实验机构与管理岗位工作人员在绩效体系方法中存在显著的博弈特点。

作为实验机构，希望评价体系公平公正，能体现出实验设备正常基本工作状态的绩效，以及通过管理岗位工作人员努力而获得的“额外绩效”，据此，实现激励。实验管理岗位工作人员希望测评模型是对己有利［8］，这是一个必须面对和解决的典型博弈问题。

1.2 设备管理绩效测评中的博弈属性

（1）实验设备管理绩效测评的动态博弈属性。区别于静态博弈策略选择的同时性，设备管理绩效测评属于动态博弈，资产管理部门和实验机构，或实验机构与管理人员作为博弈双方，在选择各自的博弈策略时是有顺序的［9-11］。

（2）实验设备管理绩效测评的完全且完美信息属性。动态博弈分为完全信息博弈和不完全信息博弈、完美信息博弈和不完美信息博弈。由于实验设备管理绩效测评中，博弈各方对信息认知对等、交流顺畅，且彼此策略公开，各自意图明朗，因此，可运用完全且完美信息动态博弈的方法进行分析［12］。

2 设备管理绩效博弈函数构建

综上所述，现以实验机构对管理岗位人员进行设备管理绩效测评，采用完全且完美信息动态博弈方法进行博弈分析，建立博弈分析模型。

依据相应文献［13-16］，可将设备管理绩效测评问题视为多阶段动态博弈进行分析［11］。具体地，可按下述过程进行分析。

2.1 确定设备管理绩效测评中的博弈基本参数

（1）实验机构对实验管理岗位人员提出仪器设备绩效要求的目标基数T（Target value）。一般地，可参考上一测评周期确定，具体可以为收费目标总金额，或设备运转总时长，文中示例分析按照“金额”，相关参数同。

（2）实验管理岗位人员明确绩效要求基数T 后，对实验机构报出一个自认为能够获得的绩效承诺数P（Promising value），即，被测评人员承诺达到的收费总金额。

之后，确定测评仪器设备的绩效商定值N（Negotiation value），为了确保N 值的合理性，需由博弈双方协商确定。绩效商定值计算式为

式中：T为实验机构提出的要求基数；P 为实验管理岗位人员承诺数；w为权值，w∈（0，1），应由实验机构和实验管理岗位人员共同确定。

取w ＞0.5 或w ＜0.5 时，分别侧重接受实验管理岗位人员承诺数或实验机构提出的要求基数；取w ＝0.5 时，则是平等考虑双方意见。

2.2 确定设备管理绩效测评中的博弈分析参数

（1）绩效增损值A′。若实验管理岗位人员的实际完成绩效（A）超过商定值N 时，超出部分以α 比例增加绩效量化值［11－15］，以实现激励人员努力提高实验设备管理的智力和精力投入。绩效增损值计算式为

式中，α为奖惩系数，α∈（0，＋∞）。

可见，当A≥N时，α表现为奖励；当A ＜N，α表现为等量的惩罚。

将（1）式代入（2）式，整理可得：

由（3）式可见，若将P 视为自变量，函数表现为“递减”，即，承诺数P值越小，绩效增损值A′越大。因此，会使得博弈失去公平，需采取措施控制。

（2）消极惩罚阈值k。为避免上述问题，模型中应建立惩罚机制。但，由于承诺数提供依据不充分，以及影响设备工作客观因素的复杂性，惩罚措施的执行需构建合理阈值。取k为消极惩罚阈值：

一般地，检测机构当次测评全部设备的消极惩罚阈值进行排序分析，当本设备对应阈值为全部阈值按大小排序的前20%时，可对本设备绩效进行消极惩罚。此处取20%，消极惩罚阈值k 排序判定可以设定其他标准，如30%等，从而加大惩罚范围。

（3）消极惩罚值A″。构建消极惩罚值A″，可按下式计算［11］：

且阈值k排序在前20%

式中，β为惩罚因子，β∈（0，＋∞）。该参数数值越大，惩罚力度就越大。

2.3 设备管理博弈绩效分析的绩效函数

根据上述分析，P 视为自变量，建立绩效函数如下：

（1）P≥A 时绩效函数的构建。绩效函数F（P）按下式计算：

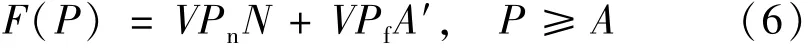
式中：VPn为基础绩效测评系数，单位可取为分/万元；VPf为绩效增损测评系数，单位可取为分/万元。

将式（1）、（3）代入（6）式，可得：

（2）P ＜A 时绩效函数。此时，存在消极惩罚问题。P ＜A，即，k ＞1，若阈值k 排序在前20%时，可按下式计算：

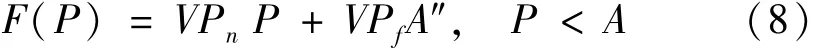
且消极惩罚阈值k排序在前20%

将式（5）代入（8）式，可得：

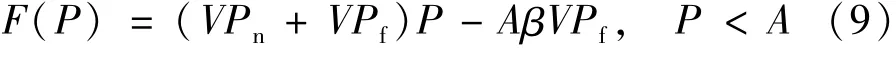
且消极惩罚阈值k排序在前20%

若阈值k排序不在前20%时，可认为，出现P ＜A情况是由于判断误差造成的，不是人为主观故意，不实施消极惩罚措施，按照下式计算：

且消极惩罚阈值k排序不在前20%

由式（7）、（9）和（10）组成绩效测评函数。

3 绩效参数对绩效测评结果的影响分析

由式（7）和式（9）可知，绩效函数表达式组成项（1－ w）（VPn－ αVPf）T、VPfαA和（VPn－ αVPf）P，存在的参数T、A和P，严格地，从数学意义上讲，均可视为自变量。其中，参数T可理解成实验机构的影响；P为管理工作人员报出策略和对实验室工作的理解准确性参数；而A 作为最终实际完成绩效，具有一定的不确定性。而函数表达式中的（VPn－ αVPf）项目尤为重要，当其大于零或小于零时，函数表现出“增减”特性。

3.1 P≥A时的绩效测评函数“增减”特性分析

（1）P≥A 时的绩效测评函数增减特性。对于式（7），鉴于上述分析，当VPn－ αVPf＞0 时，即，VPn/VPf＞α时，式（7）中的所有组成项均大于0；VPn/VPf＜α时，式（7）中的项（1 － w）（VPn－ αVPf）T 和（VPn－αVPf）P均小于0。

（2）基于函数“增减”特性的参数设置策略。对于式（7），其成立条件P≥A，即，实验管理岗位人员承诺数大于实际完成绩效。由式（1）可知，N ＞P，即，满足N ＞P≥A。可见，此时，可判定为A值异常，未达到一般绩效水平。此时需判定设备在测评周期内是否有客观原因造成长期停用、效率低下，以及收费项目遗漏等问题？如没有类似的客观原因，可考虑将此时的绩效测评函数定义成“递减”函数，即，取VPn/VPf＜α。鉴于该比值的重要性，将其定义为激励指数（Incentive index），简称Ii，即：

此外，若A 值的异常存在直接的客观原因，绩效可按常规绩效按式（10）计算。

（3）VPn/VPf＝α 时的绩效函数表达。当VPn/VPf＝α时，即，VPf＝VPnα，式（7）简化为：

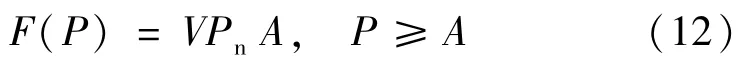
即与式（10）表达式相同。

3.2 P ＜A时的绩效测评函数“增减”特性分析

对于式（9），其组成项（VPn＋VPf）P 和A、β、VPf，含有两个变量参数，A是测评周期末才会获得的参数，存在一定不确定性，可将其作为自变量分析。当P 为定值时，函数呈现递减特点，消极惩罚特征突出。

4 设备管理绩效测评的博弈分析

以某教学岗位2 名工作人员负责的27 台设备的绩效测评数据为例进行分析。2 名工作人员所管理的设备分别为序号1 ～15、16 ～27。

4.1 不考虑函数特性的示例绩效测评分析

（1）均衡考量实验机构和管理岗位工作人员双方意见，取w ＝0.5。

（2）为了激励工作人员，取α ＝0.7。

（3）惩罚因子β不宜设置过大，取β ＝0.6。

（4）参照本机构相关的教学科研绩效测评取值，VPn取2.5 分/万元，VPf取4 分/万元。

按上述模型进行分析，结果见表1。

表1 某实验机构两名工作人员设备管理绩效测评结果

4.2 考虑函数特性的示例绩效测评分析

（1）参数设定。对于式（7），当P≥A，且取Ii＜α时，突出绩效的激励机制。按上述示例，取α ＝0.7 分析；VPn取为2.5 分/万元，保持不变，而VPf变为5分/万元，使得Ii＝0.5。其他参数均与上节分析一致。

（2）考虑函数特性的绩效博弈测评分析。参数如前文所述。另，取VPf＝7.15 分/万元，此时Ii＝0.35，及结合上例的Ii＝1 和0.625 的结果进行分析。分析数据列于表2。

表2 激励指数Ii 不同取值时绩效分析结果对比

将甲、乙绩效分随参数变化及激励指数Ii不同取值的关系进行分析，如图1 所示。

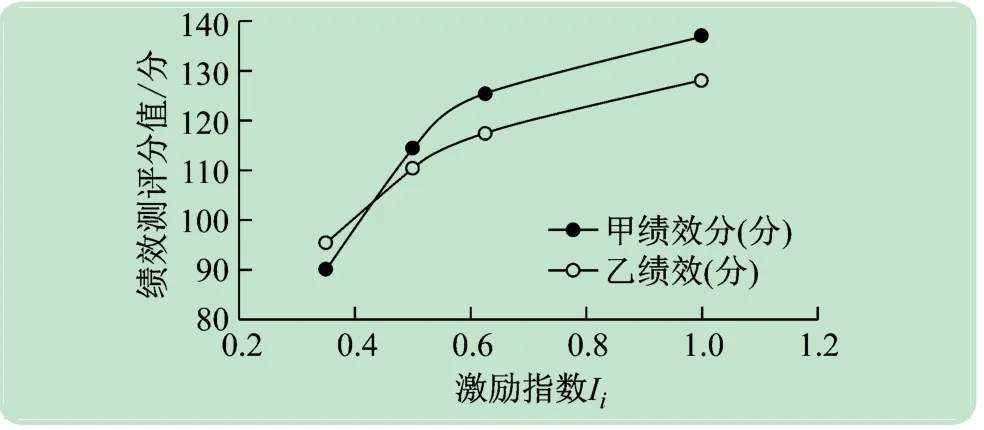
图1 不同激励措施下两名工作人员设备管理绩效对比

可见，随着激励指数Ii的减少，绩效分降低，两位被测人员的绩效分差减小；在Ii＝0.43 时，两位被测人员的绩效分相等，之后乙绩效分反超；与常规测评相比，单独设备绩效测评极差变化范围在5% ～110%间；对于两位被测评人员，不同参数测评分析的绩效分极差变化达到25% ～35%。可见，激励指数Ii属敏感参数，其与绩效测评分表现出显著的正相关。

此外，由图1 分析可见，关系曲线中存在拐点，对应甲的约为Ii＝0.53 ，对应乙的约为Ii＝0.55，即，当激励指数小于0.55 时，随着指数的减小，绩效测评分锐减。

通过各设备绩效测评值与常规测评比较，设备的绩效值有增加、减小和基本持平。可见，该方法克服以往简单方式的测评，实现了激励、奖惩的目的。

5 结 论

本文采用博弈理论方法分析设备绩效管理问题，结合问题的博弈过程，分析提出模型参数和博弈函数；依据博弈原理和实际问题，设定参数范围；考虑奖励激励机制，设定控制参数；通过示例分析模型的可行性，提出敏感性参数及其控制机制。研究结论如下：

（1）应用动态博弈理论分析设备绩效管理问题需明确博弈属性和博弈过程。结合博弈过程分析，可保证绩效模型构建的完整性。

（2）绩效增损值、消极惩罚值的设置，使得依赖博弈函数模型进行的绩效测评更具激励特征，与常规比较，实现了显著的奖惩特点。

（3）模型参数设置策略是模型功能的关键，例如，β、VPn和VPf值的确定，控制Ii＜α可实现绩效测评的激励目的，并保证绩效测评的合理性。