基于改进模糊聚类算法的地铁站点重要性分析

张 玲， 郭进利

(上海理工大学 管理学院， 上海 200093)

地铁是城市公共交通中最重要的一环，与其他交通方式相比有着快速便捷、载客量大、准时等优越性，成为可以解决大城市区域交通需求的关键方案[1]。随着城市地铁的发展，世界上的许多城市对地铁系统的依赖日益增长。截至2019年6月，上海已有17路线、415座车站、累计705 km地铁运营线投入使用，运营线网规模位居世界前列(含磁悬浮)。

城市地铁网络中的节点因其重要度不同，遭受攻击后失效导致的网络运行效率的降低程度有所不同。已有研究表明，交通网络的网络抗毁性是由关键节点决定的[2]。因此识别地铁网络中对网络运行效率起着重要作用的关键节点，加强对关键节点的保护和管控，增强其抗风险能力，对于提高地铁网络的抗风险能力有重要意义。目前，已有许多学者对地铁网络和复杂网络节点重要度评价进行了深入研究。在对波士顿地铁网初步的研究中，Latora等[3]发现其具有小世界特性。Sienkiewicz等[4]研究了22个所在波兰的城市轨道交通的网络特性，从而分析得出波兰轨道交通网络呈现出小世界特性和分层组织的结论。Meng等[5]用Space-L和Space-P两种模型建立深圳市地铁网络，构建两种模型的节点重要度评价模型，对两种模型的抗毁性进行对比，结果表明P模型比L模型具有更强的整体抗攻击能力，更有利于网络的弹性。郭晓玲等[6]运用二次约束二次规划模型，针对赋权网络，综合考虑节点移除后对网络的整体结构和功能的影响，给出了计算网络连通性的新测度，即一步连续和两步连续。韩纪彬等[7]采用了空间 L 方法系统分析其网络特征参量，从最大连通子图的相对大小、网络全局效率和网络局部效率等指标分析网络的可靠性。许海霖等[8]结合垂面距离和灰色关联度综合评价方案，用局部熵代替整体熵改进TOPSIS算法，测算了地铁网络的节点重要度。王梓行等[9]创新性地重新定义了复杂网络的冗余度，并重新定义的冗余度量化了网络抗毁性，利用节点删除法对节点重要度进行了评估。

目前对地铁网络节点重要程度的评价主要依赖于删除节点，考察节点失效对网络整体效率的影响，且在评价节点时多采用重要度排序，但是在交通网络中，对一个节点的评价大多为“关键”“重要”“一般”等表达，研究者难以确定关键节点的数量，选择重要度排序前K个节点作为关键节点，导致关键节点判别不准确。为准确判断轨道交通的关键节点，本文选取节点介数、接近中心性和特征向量中心性作为重要性评价指标，研究一种基于特征加权的模糊聚算法的节点重要性评价方法，适用于地铁网络。

1 城市地铁网络构建及指标选取

1.1 城市地铁网络构建

城市地铁网络建模是指将地铁按照一定方法抽象为复杂网络拓扑结构，从而方便对复杂网络的各个统计指标进行分析和计算，为节点重要性分析提供模型基础[10]。为直接反映站点之间的连接关系，采用Space-L方法来构建城市地铁网络拓扑结构：将站点抽象为节点，相邻站点之间的轨道线路抽象为边，构建城市地铁网络的自然拓扑结构，如图1所示。

图1 Space-L法构建网络拓扑图

1.2 指标选取

从网络拓扑结构出发，综合考虑了节点自身的性质及其邻居节点的性质，最终选取了节点的介数、接近中心性和特征向量中心性作为评价节点重要性的依据。在描述网络中某一个节点时，节点介数描述了该节点进行最短路径传输信息的控制能力，接近中心性描述了网络中所有节点到该节点的效率，特征向量中心性反映了与该节点相邻节点的重要性。

1)介数：以经过节点i的最短路径数目来刻画节点重要性的指标称为介数，它描述了节点i对于网络中节点对之间沿着最短路径传输信息的控制能力，即

(1)

式中：σst(i)表示节点s和节点t经过节点i的最短路径数；σst表示节点s和节点t之间的最短路径数。在现实出行中，人们往往选择最短路径。因此，通过节点的最短路径越多，节点越重要。

2)接近中心性：对于网络中的任意节点i，可以计算该节点到网络中所有节点的距离的平均值，平均距离越小，代表节点i更接近其他节点，将平均距离的倒数定义为节点的接近中心性，即

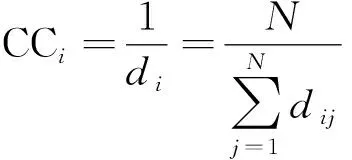
(2)

3)特征向量中心性：特征向量中心性的基本思想是一个节点的重要性既取决于其邻居节点的数量，也取决于其邻居节点的重要性。本文将特征向量中心性定义为节点的邻居节点的度值累加，即

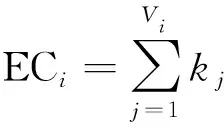
(3)

式中：Vi为节点空间V的子空间，表示节点i的邻居节点集合；kj为节点j的度值。由于特征向量中心性的计算方法既考虑到了节点i邻居节点的数量，即度值，又考虑到了邻居节点的质量，为了减少指标之间的相关性，本文不再引入度值作为评价指标。

2 基于k-means和熵权法加权的改进FCM算法

不同于聚类算法的硬化分，严格地将个体归划到某一类去，模糊聚类将个体以一定的隶属度归于某一类，实现软化分。在交通网络中，对节点的描述多是“关键”“重要”等模糊性表达，研究者难以对其进行明确的区分，因此模糊聚类更能客观描述节点重要性程度。

基于上述结论，选择采用模糊C-均值(FuzzyC-means)对节点进行模糊聚类。FCM算法是利用目标函数来反映聚类效果，利用约束条件解决非线性问题，目标函数进行不断迭代，直到取得极小值。在模糊聚类的思想中，每一个样本不是严格地归为某一类，而是以一定的隶属度属于某一类。为了优化FCM算法，从而进一步提升FCM算法在地铁网络中的适用性，本文采用k-means和熵权法对FCM算法进行改进。

2.1 基于k-means的初始聚类中心确定方法

FCM算法对初始聚类中心十分敏感。初始聚类中心的选取直接影响算法迭代次数和计算时间，算法极容易因选择了不恰当的初始聚类中心而陷入局部最优解[2]。

k-means作为动态聚类法，具有原理简明、熟练快速、聚类效果较优等优势[12]，是一种最为广泛使用的聚类方法，且可以得到与FCM相似的聚类中心，因此在对数据进行模糊聚类之前，先使用k-means 聚类，确定初始聚类中心，不仅可以大大降低迭代次数，而且可以降低FCM陷入局部最优解的可能性。

2.2 特征加权的FCM算法

为了优化传统FCM算法，除了通过k-means动态聚类法确定初始聚类中心，减少迭代步骤之外，也重新定义了样本与聚类中心之间的距离。

考虑到节点介数、接近中心性和特征向量中心性3个指标在重要性评价上的权重有所不同，熵权法是一种客观赋权方法，指标的变异程度越小，其反映的信息量就越少，所对应的权值应该就越低，因此在传统FCM算法基础上使用熵权法引入权重。

特征加权后的FCM算法与传统FCM算法的区别体现在样本xj与聚类中心ci之间的距离变为

(4)

式中：wq为相应指标的权重；xjq表示第j个样本的第q项指标；ciq表示第i个聚类中心第q项指标；m为模糊加权指数，取值范围为1.5～2.5。因此，改进FCM算法目标函数和约束条件为

(5)

式中：c为别个数；uji表示第j个样本属于第i类的隶属度，满足0≤uji≤1且uj1+uj2+…+ujc=1。

改进FCM算法的步骤如下：

步骤1l=0，通过k-means算法得到初始聚类中心C(0)，确定初始隶属度矩阵U(0)，通过熵权法计算的指标权重为W。

步骤2l=l+1，更新第l步中的聚类中心C(l)，即

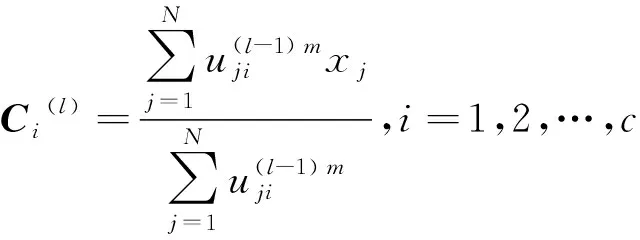
(6)

步骤3修正隶属度矩阵U(l)，计算目标函数J(l)，即

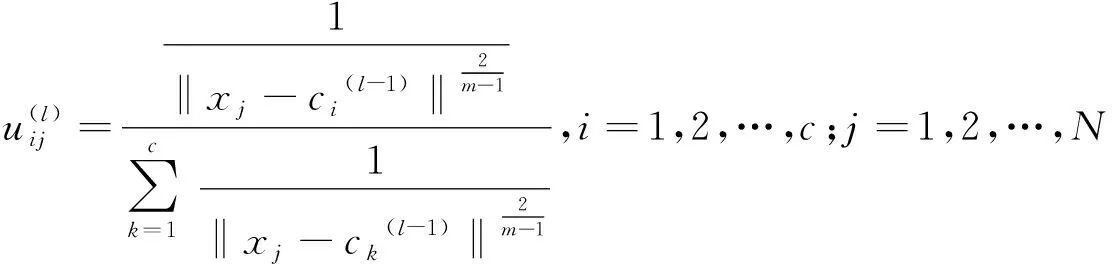
(7)

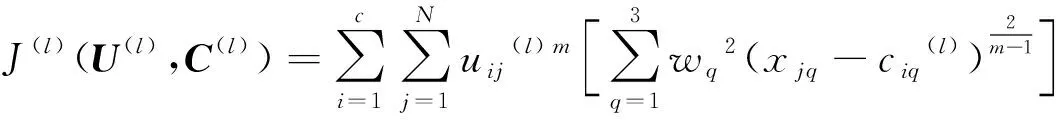
(8)

步骤4对给定目标函数终止容限ε或最大迭代步长Lmax，当|J(l)-J(l-1)|<ε或l>Lmax时，终止迭代，否则l=l+1，转步骤2。

2.3 算法检验

为了判断FCM算法的准确性，采用误差率交叉估计法进行结果验证[12]。首先从N个数据中任意去掉一个，对其他数据进行FCM聚类，然后用所得的聚类中心对删除的样本进行判别。重复上述步骤，直到所有样本均被检验，与原FCM聚类结果进行对比，求得误判率。

3 实证分析

选取上海地铁网络作为研究对象，以截至2019年6月的地铁站点及线路为例，验证评价方法的有效性。

3.1 方法应用

将上海地铁实际网络抽象为以站点为节点、站点之间的轨道为连边的Space-L网络模型，由于地铁相邻两站之间的出行时间多为2～3 min，故不考虑站点之间的距离，建立无向无权复杂网络模型，如图2所示。

图2 上海地铁Space-L模型

由Gephi软件的结果可知，节点度最大的点为世纪大道，度值为8，上海地铁网络平均度为2.329，大多数站点的度值为2，即与同一条线路上的相邻两站构成邻居关系，网络直径为44。平均路径长度为15.893，网络平均聚类系数为0.026，上海地铁Space-L网络不构成小世界网络。

通过MATLAB计算出节点介数、接近中心性和特征向量中心性3个指标，并对所有的数据进行标准化处理。

通过熵权法对网络节点重要性指标进行加权，得到3个指标(节点介数、接近中心性、特征向量中心性)的权重矩阵为W={0.425 7 0.165 8 0.408 5}。

3.2 改进FCM算法的应用结果

将节点重要性分为5个级别，分别为“关键”“次关键”“重要”“较为重要”“一般”。在应用算法的过程中，取聚类类别数c=5，终止容限ε=0.001，模糊聚类指数m=2，最大迭代次数Lmax=1 000，通过改进FCM算法得出的聚类结果如图3所示。

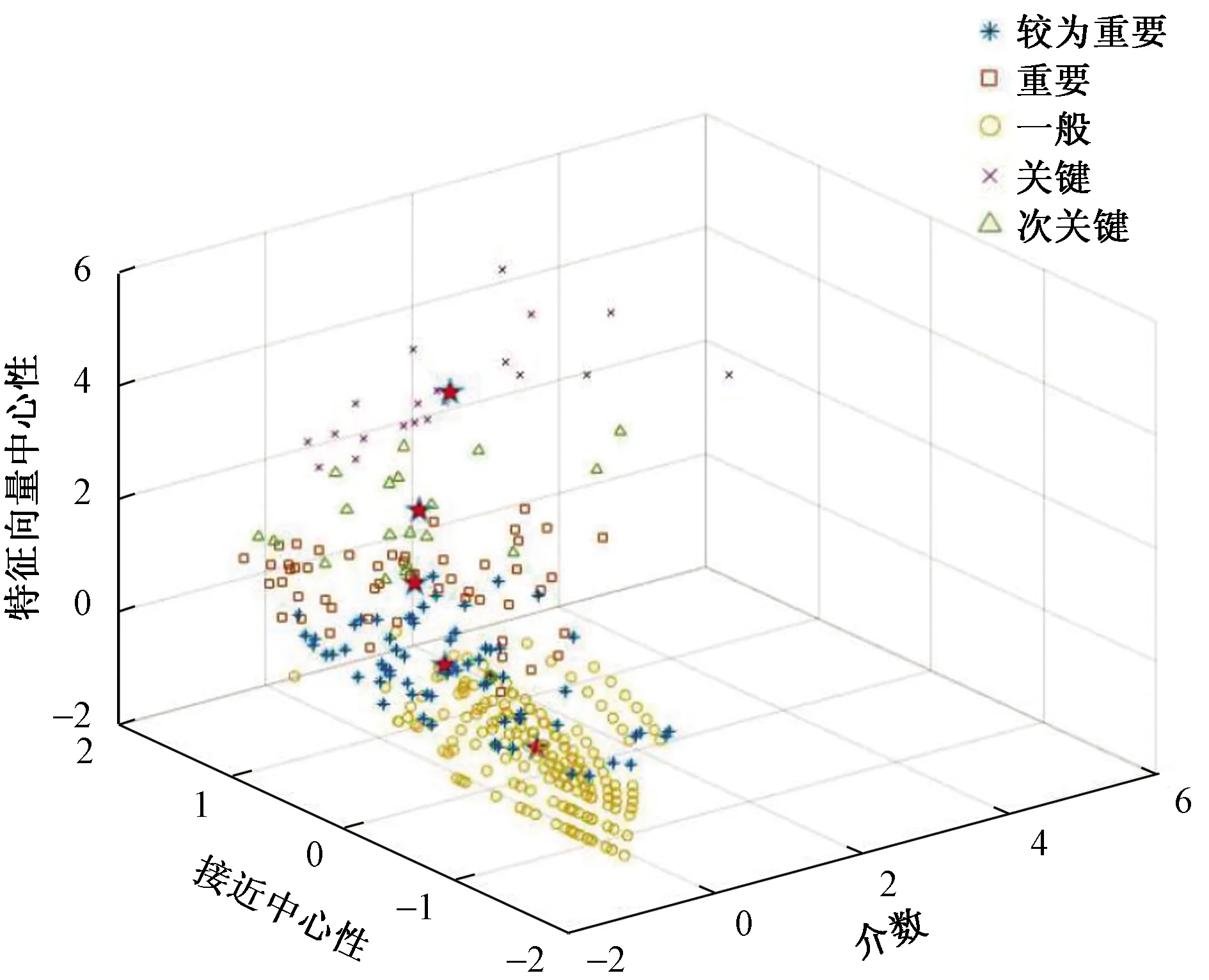
图3 改进FCM聚类结果可视化

由于节点介数、接近中心性和特征向量中心性均为正向指标，即指标数值越大，节点越重要，因此将最终聚类中心的3项指标加权和进行降序排列，将类别依次记为“关键”“次关键”“重要”“较为重要”“一般”，改进FCM算法结果统计如图4所示。

图4 上海地铁站点重要性汇总

由图4可知，用改进FCM算法得出了上海地铁的24个关键节点、52个次关键节点、62个重要节点、167个较为重要节点和41个一般节点。对比站点信息得出关键节点分别为上海体育馆、徐家汇、常熟路、陕西南路、人民广场、汉中路、江苏路、静安寺、南京西路、世纪大道、宜山路、金沙江路、曹杨路、大木桥路、东安路、肇嘉浜路、成山路、陆家浜路、曲阜路、嘉善路、马当路、交通大学、新天地、隆德路。由站点信息可知，关键节点均为换乘站点，且地理位置集中于市区中心区域。

表1所示为改进FCM算法各个聚类中心在3个评价指标上的得分。从表1可知，关键节点在介数、接近中心性和特征向量中心性上的评分均为最高，其中特征向量中心性的得分为2.705 6，说明相邻节点的重要性对节点自身的重要性有一定影响。次关键节点的聚类中心在3个评价指标上的得分仅次于关键节点，且依然是在特征向量中心性这一指标上得分最高。重要节点在接近中心性上的得分较高，说明此类节点与网络中节点的距离较小。图4 表明，较为重要站点个数为167个，这些站点大多居于线路的中间部分，且不为换乘站，经过此类站点的最短路线较多。

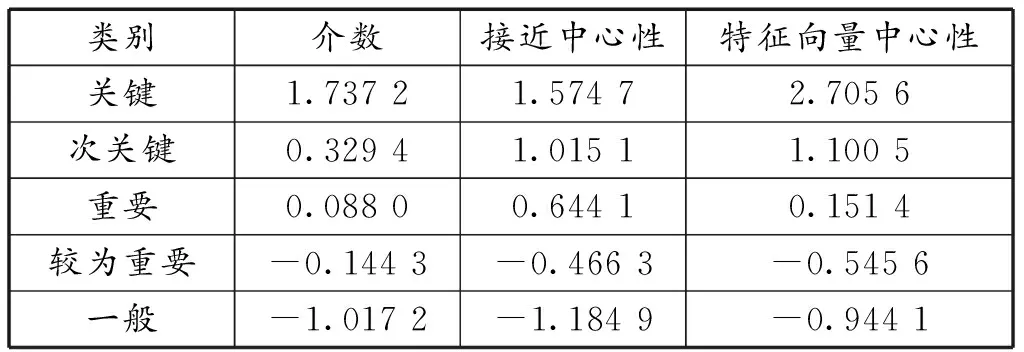
表1 聚类中心

而在重要性为一般的节点中，大多数节点为地铁线路的首末站点或与首末站点相邻的站点。在地铁网络拓扑结构中，这些站点一般不与其他站点相邻，度值较小；通过它们的最短路线较少，因此介数较小；而其他站点到它们的距离较大，因此接近中心性较小；由于在模型中考虑到了一个节点的重要性也取决于其邻居节点的重要性，因此与首末站点相邻的站点在评价体系中重要性也相对较小。

3.3 改进FCM算法评价

3.3.1 目标函数及迭代次数

与传统FCM算法相比，由于改进FCM算法在迭代之前通过k-means确定了初始聚类中心，故初次计算的目标函数值和迭代次数均远低于传统FCM算法。传统FCM算法迭代次数为62次，改进后迭代了26次，迭代次数降低了58.06%，缩短了运行时间。传统FCM的目标函数值为5.554 9，改进FCM算法最终得出的目标函数值为5.259 1，目标函数值降低了5.33%，如图5所示。

图5 目标函数和迭代次数对比

3.3.2 误判率评价

采用误判率交叉估计法，分别验证传统FCM算法与改进FCM算法的误判率。观察表2可知，使用传统FCM算法进行模糊聚类，在“重要”“较为重要”“一般”3种类别中出现分别出现了6、9、4个误判，整体误判率为5.49%。而使用k-means和熵权法对FCM算法进行改进后，误判率为0，大大提高了FCM算法的准确性。

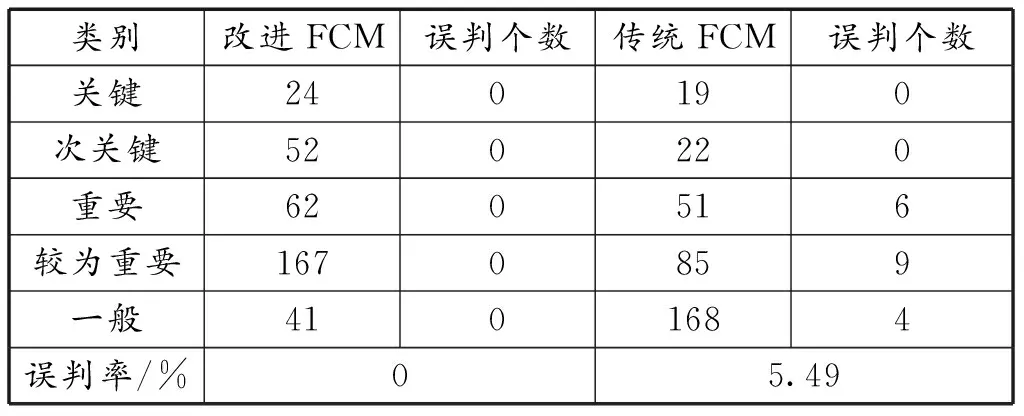
表2 改进FCM算法与传统FCM算法误判率对比

4 结语

研究了城市地铁网络节点重要性：选取节点介数、接近中心性和特征向量中心性3个指标，通过基于k-means和熵权法改进的FCM算法进行模糊聚类分析，并由模糊聚类中心3项指标的加权和将地铁网络节点分类为“关键”“次关键”“重要”“较为重要”“一般”5个重量级类别。以上海地铁网络为例，通过模糊聚类得出了24个关键节点，均在4号线环线及以内区域，因此在以后的站点维护中，要加强对城市中心区域地铁站的维护，增强其抗干扰能力。对比改进FCM算法和传统FCM算法的聚类效果，发现改进后的FCM算法降低了目标函数值、减少了迭代次数、降低了误判率，更能客观刻画地铁网络的节点重要性，适用于城市地铁网络。

提出了一种改进的FCM模型，但仍存在许多方面期待进一步研究，例如本文仅从网络拓扑结构上综合考虑了节点本身及其相邻节点的重要性指标，但并未考虑实际交通需求量，以后的研究可以将实际客流量考虑进去，建立带有权重的网络模型，计算各个节点的强度作为指标之一。