应急物资配送问题研究

王金英，包立军

应急物资配送问题研究

王金英1，包立军2

（1.辽宁工业大学 理学院，辽宁 锦州 121001；2.锦州市公安局 网络安全保卫支队，辽宁 锦州 121001）

研究了多受灾点的应急物资运送方案的优化问题。首先将各城市路径分布图进行简化，对各节点重新编号，采用Floyd算法求出各城市运送物资到达受灾地所需要的时间，建立了一个多目标应急物资配送模型并进行求解。其次，建立了基于双层规划方法的应急物资配送模型，采用动态优选策略求得全局满意应急方案。最后，为实现整体救灾目标，求得了近似最优解作为应急物资运送方案。

最短路径；Floyd算法；资源竞争；动态优选策略

当今我国经济飞速发展，各类公共突发应急事件时有发生，使人类的生命和财产遭受严重损失。灾后初期受灾地区往往需要大规模的应急救援物资，为保证应急物资的配送时效，提高救援效率，有必要对应急物资配送方案的优化问题进行研究，这具有重要的理论和实际意义。

目前，对于应急物资配送方案问题的研究也较多，如文献[1]研究了物资需求约束条件下多出救点的紧急物资调度问题。文献[2]建立了一种双层决策方法的应急资源配置模型，确保配置过程兼顾公平性和及时性。文献[3]建立了随机混合整数规划模型，据此讨论了应急物资储备地点和仓库的库存水平。文献[4]构建了一个多目标优化模型，对应急物资配送车辆路径安排以及配送中心选址等问题进行决策。文献[5]建立了物资动态分配和配送中心选址的多目标规划模型，并设计了一种非支配排序的遗传算法进行求解。文献[6]构建了应急物资公平配送的多目标车辆路径优化模型，并用MATLAB进行求解。文献[7]建立了考虑受灾点需求时间窗的多目标应急物资车辆配送路径规划方案模型，并运用遗传算法求解。文献[8]引入公平理论，构建了关于效率和公平的双目标优化模型，并利用改进的遗传算法实现物资配送优化。上述文献虽然成功地得到了应急物资配送的最优解，但大多局限于将单受灾点作为研究对象，当多地同时受灾，各受灾点资源需求存在竞争时，各单受灾点最优解的累加甚至不是可行方案。因此，本文针对多受灾点情形，在满足资源连续性的条件下，建立了多受灾点-多出救点的应急资源配置模型，并通过MATLAB求解。

1 问题的提出

某省份各个城市的分布情况如图1所示，图中的直线段代表连接各个城市的公路，直线段上的数值代表车辆通过这段路程所需要的时间。目前有3个地区突然发生自然灾害，各受灾地记为A1、A2、A3，所需应急物资分别为100、80、60 t/a；能够供应应急物资的城市为C1，C2，…，C12，这些城市能供应的应急物资为30、15、15、20、35、40、30、20、10、25、25、30t/d。

问题一：若C1，C2，…，C12供应的应急物资成本是2，4，5，3，1，6，2，3，6，1，5，5万元/(t·h)，为保证受灾地A1、A2、A3每天需求的应急物资，请帮助设计一份经济快捷的运送方案。

问题二：若每小时消耗应急物资5 t，为灾害爆发后应急物资能尽快运送至A1、A2、A3三地并保证连续供应，请帮助设计一份救灾第一天的运送方案。

问题三：若希望应急物资能够在灾害发生后5 h之内送达且保证连续供应，请修改问题二的运送方案。

图1 某省份各城市的分布图

2 基本假设与符号说明

2.1 基本假设

假设1：运输过程中没有突发事件发生，保证耗时为图中标记量。

假设2：应急物资在运输过程中损坏率为零。

假设3：所有装卸时间及费用忽略不计。

假设4：配送车辆能够容纳各城市提供的应急物资。

2.2 符号说明

3 模型的建立与求解

3.1 问题一的建模与求解

将各城市的分布图(图1)简化，去掉图中无效的节点和路径，对简化后的路径图各节点重新编号(图2)，以便下一步求解各城市到达受灾地区的时间。

接下来，求各城市运送应急物资到达受灾地的时间，即求各城市对应的节点到受灾地对应的节点之间的最短路径。本文采用Floyd算法[9-10]进行求解，结果整理后如表1所示。

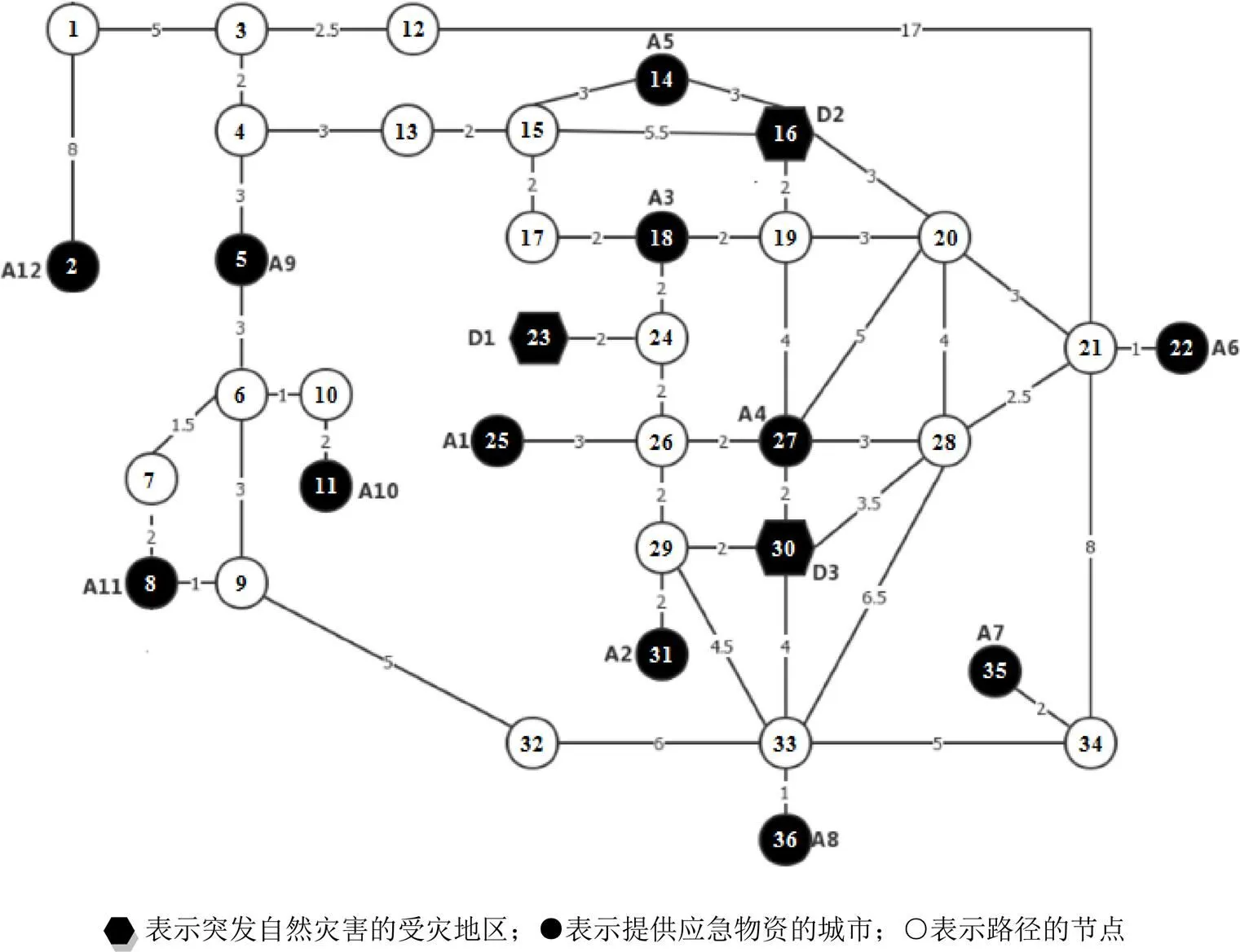
图2 重新编号后的路径图

表1 各城市到达受灾地的时间

采用矩阵形式表示任意全局方案为：

运送方案总代价为：

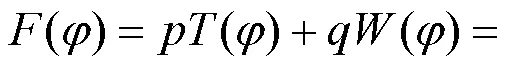
约束条件为：

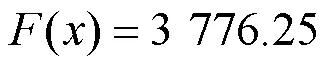
表2 各城市到受灾地的运送方案（p = q = 0.5）

由表1可知，C12运送应急物资到达A1、A2、A3所需时间分别为28、25.5、32 h(均超24 h)，即C12提供应急物资不能于当日送达受灾地，而其余11个城市都可在当天内将应急物资送达到受灾地。因C12提供物资不能于当日到达，C12所提供物资将计入次日提供物资量。由于灾害发生后第一天内无法接收到C12的物资，因此，第一天需要单独考虑，于是计算第一天的分配方案时，需除去C12对应的3个变量。再根据表2可知，运送方案中C12未参与救援，因此，除去C12对应的3个变量后，运送方案保持不变，即问题一的应急方案为：

3.2 问题二的建模与求解

约束条件为：

观察上述方案，发现各出救点之间存在资源竞争，所以，A1、A2、A3 3地的独立最优解累加是不可行的。动态优选策略的核心思想是在得到各受灾点独立最优应急方案(具体算法见文献[1])的情况下，检测存在竞争的出救点及竞争资源量，从未被利用的资源中找到可以满足各受灾点应急最早开始时间延长量之和最小，且费用最少的调整方案。通过动态优选策略(具体算法见文献[2])，对上述方案进行调整，得到全局满意应急方案：

3.3 问题三的建模与求解

为更好地对受灾点进行救援，实现整体救灾目标，设计了一种近似最优解。将C3向A1提供物资的发货时间延迟0.5 h，C5向A2提供物资的发货时间延迟2 h，通过求解，得到全局满意应急方案：

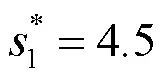
4 结束语

首先根据权重、的不同取值情况，设计了各城市提供应急物资运送到各受灾地的3种方案，可以依据具体的实际情况选择参数、的值，从而得到经济快速的应急物资运送方案。其次考虑了“时间最短、持续供应”的条件，求得了符合要求的近似最优解。最后为实现整体救灾目标，设计了一种应急物资运送方案。本文的这类问题有很强的应用背景，广泛适合于大型火灾、危险化学品泄漏、电力系统故障、网络系统瘫痪等灾害的应急。

[1] 刘春林, 施建军, 何建敏. 一类应急物资调度的优化模型研究[J]. 中国管理科学, 2001, 9(3): 29-36.

[2] 王苏生, 王岩. 基于公平优先原则的多受灾点应急资源配置算法[J]. 运筹与管理, 2008, 17(3): 16-21.

[3] 王亮, 邱玉琢. 两级应急物资储备协同预先配置优化决策研究[J]. 软科学, 2015, 29(12): 117-120.

[4] 陈刚, 付江月. 基于NSGAII的应急物流多目标LRP研究[J]. 软科学, 2016, 30(4): 135-139.

[5] 曲冲冲, 王晶, 黄钧, 等. 考虑时效与公平性的震后应急物资动态配送优化研究[J]. 中国管理科学, 2018, 26(6): 178-187.

[6] 张杏雯. 模糊条件下应急物资公平配送多目标优化模型[J]. 物流科技, 2019, 42(5): 20-24.

[7] 吕伟, 李志红, 马亚萍, 等. 考虑受灾点需求时间窗的应急物资配送车辆路径规划研究[J]. 中国安全生产科学技术, 2020, 16(3): 5-11.

[8] 张杏雯, 倪静. 公平约束下的应急物资配送模型及算法[J]. 统计与决策, 2020, 36(7): 179-182.

[9] 陈华友, 周礼刚, 刘金培. 数学模型与数学建模[M]. 北京: 科学出版社, 2014.

[10] 王翼. MATLAB基础及在运筹学中的应用[M]. 北京: 机械工业出版社, 2012.

Research on Distribution of Emergency Materials

WANG Jin-ying1, BAO Li-jun2

（1. College of Science, Liaoning University of Technology, Jinzhou121001, China;2. Network Security Detachment, Jinzhou Public Security Bureau, Jinzhou121001, China）

This paper studies the optimization of emergency supplies transportation scheme for multiple disaster areas. Firstly, the route distribution map of each city is simplified, and each node is renumbered. Floyd algorithm is employed to calculate the time required for each city to transport materials to the disaster-stricken area, a multi-objective emergency materials distribution model is established and solved. Secondly, the emergency material distribution model based on the bi-level programming method is established, and the dynamic optimization strategy is adopted to obtain the overall satisfactory emergency plan. Finally, in order to achieve the overall disaster relief goal, the approximate optimal solution is obtained as the emergency material transportation scheme.

shortest path; Floyd algorithm; resourcecompetition; dynamic optimizing strategy

10.15916/j.issn1674-3261.2021.05.011

O221

A

1674-3261(2021)05-0325-05

2021-03-04

辽宁省教育厅高校科研基金(JJL201915403)

王金英(1981-)，女，辽宁黑山人，副教授，硕士。

责任编辑：孙 林