一种锥壳形旋转超声电机的结构设计与模态分析

赵彦东，何 勍，余祥瑞

一种锥壳形旋转超声电机的结构设计与模态分析

赵彦东，何 勍，余祥瑞

（辽宁工业大学 机械工程与自动化学院，辽宁 锦州 121001）

为了解决面内弯曲旋转行波电机转子与振子稳定接触困难的问题及面外弯曲旋转行波电机运转时转子径向滑移问题，提出了一种锥壳形旋转行波超声电机。锥形超声电机振子与转子为锥面接触，可以将面内振动与面外振动耦合。利用有限元软件确立了振子的工作模态、固有频率及结构尺寸，为锥形超声电机的后续研究奠定基础。

锥壳；超声电机；旋转行波；模态分析

超声电机是根据逆压电效应激励出频率大于20kHz机械振动，利用该振动实现转子在定子上运动的一种微型压电驱动装置。因其毫秒级响应、高精度定位、噪音小、能量损耗低、无电磁干扰、体积小、低速大转矩等诸多优点近几十年来引起广泛关注[1-3]。目前，市面上出现多种多样、多种功能的超声电机,根据驱动原理的不同，超声电机可以分为驻波型、行波型超声电机。就目前商品化应用方面来讲，行波型超声电机属于发展较为完善的，常见的行波型超声电机有圆盘状的、柱状的等[4-6]。

旋转行波超声电机按工作模式可以分为面内弯曲振动和面外弯曲振动。采用面内弯曲振动模式的电机可在振子的内侧或外侧获得椭圆运动，但实现转子的稳定接触比较困难[7]。利用面外弯曲振动模式的电机是在振子的端面获得椭圆运动，由于振子与转子的端面是水平的，转子在运转时会产生径向滑移[8]。为了克服以上旋转行波超声电机存在的缺点，本文提出了一种形状新颖的锥壳形旋转行波超声电机。

1 电机的结构

图1所示为锥壳形超声电机的结构示意图。超声电机振子采用锥壳形中空结构，锥壳中空部分用于布置转子及其输出轴。电机转子设计为圆锥实体，与锥形振子内部倾斜表面为锥面接触，这样可以减小转子与振子间的径向滑移而带来的能量损失。转子通过轴承，卡簧压紧在振子上，可以实现预紧力的施加。本电机结构简单，体积小，不需要传动机构，可以根据实际应用场景的不同，进行结构融合设计。

图1 电机结构

2 电机的工作原理

本超声电机为锥壳形旋转行波超声电机，由于其本身的对称结构，振子能够在同一频率激发出空间相位差为π/2的A、B两个正交的振型。在锥壳大端端面半径为处，A、B两相在法线方向的第阶弯曲振型函数可表示为

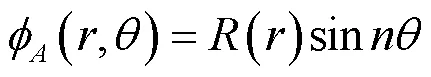
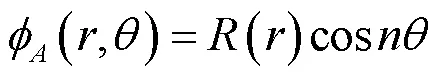
式(1)、(2)中：()为沿半径方向的位移分布函数；sin，cos为沿周向的位移分布函数。

在无其他模态干扰的情况下，用时间上相差π/2的两相激励信号同时施加在激发相应模态的压电陶瓷片上，能激励出振子的在空间和时间上都相差1/4周期的弯曲模态，即复合成一个沿圆周方向行进的行波。

3 振子结构设计与模态选取

对于目前已有旋转行波超声电机的振子模态，一般选择面内弯曲模态或面外弯曲模态。本文所设计的振子与传统的旋转行波超声电机模态的选取不同，无需甄别轴向弯曲模态与径向弯曲模态。这是由于锥壳的特殊结构所决定的，在一个振型下既有轴向弯曲振动，又有径向弯曲振动，模态属于二者的耦合。

根据超声电机的工作原理可得知，对超声电机的振子进行模态分析设计，可以得到振子相应的固有频率，使振子在实际工作中通过共振来获得最大的振幅，因此振子的模态设计是超声电机设计中最关键的步骤。

参考USR30旋转超声电机的振子端面尺寸，并将本电机振子的锥壳的半锥角选择为45º，振子的形状及主要结构参数如图2所示。

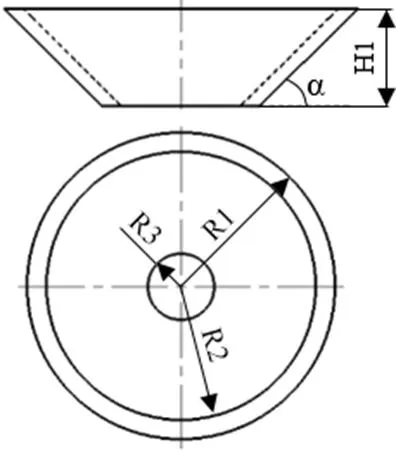
图2 振子尺寸参数图

材料的选取对振子频率的影响很大。本文在振子尺寸参数不变的条件下，分别考虑了铝合金、45#钢、黄铜作为基体材料时的弯曲振动频率。相同结构参数时同阶弯曲振动模态，材料为黄铜的振子频率较低，材料为铝合金的振子与45#钢的振子在同阶弯曲振动模态下模态频率较为接近。考虑到电机的工作频率应高于超声的临界值以及振子齿在实验过程的耐磨强度，在本论文中,振子的材料选择45#钢。

利用有限元ANSYS软件对振子进行有限元仿真，仿真模型的具体参数设置见表1。

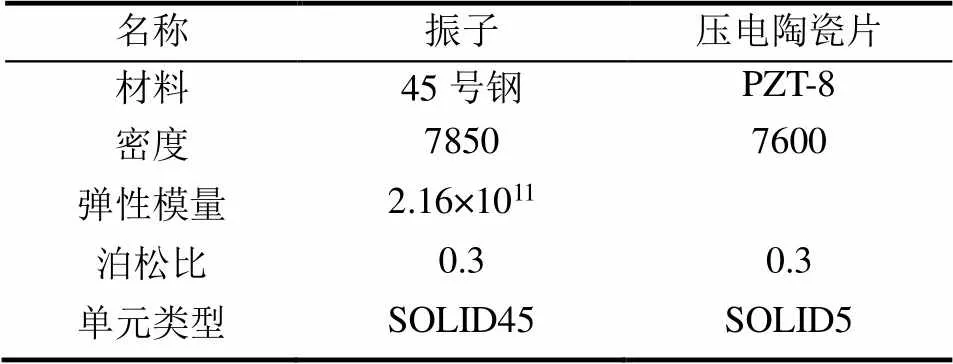
表1 态分析参数设置表

根据具体参数下的仿真结果，振子的弯曲模态结果中有第三(=25 954.6 Hz)、四阶(=39 166.5 Hz)模态可以作为振子的工作模态，结果如图3所示。

图3 振子弯曲模态

对于锥壳形振子，为了激发出振子的固有模态，图3中3个模态的压电陶瓷片布置方式是有所不同的，三阶模态的压电陶瓷片每隔90°布置，四阶模态需要每隔22.5°布置压电陶瓷片。从压电陶瓷片的布置角度，三阶弯曲模态的布置更容易设计。三阶模态的频率为25 954.6 Hz，满足超声要求，综上选择三阶弯曲模态为工作模态。

振子处于三阶弯曲模态时，由于圆锥形振子结构的对称性，在同一频率下有A、B两个弯曲模态，模态如图4所示。

图4 三阶弯曲模态

经过模态分析与选取，电机尺寸参数确定为：圆锥母线与轴线呈45°夹角，大端面外径为30 mm，小端面外径为10 mm，壁厚为2.83 mm，圆锥台高为10 mm，驱动齿高2 mm，驱动齿外径32 mm。由于振子为圆锥台壳对称结构，驱动齿的数量应为4的倍数，且应为振子三阶模态的倍数[9]，为了同时满足以上两个要求，齿数确定为72个。

振子为锥壳形，为使压电陶瓷片容易粘贴在振子锥面上，对振子锥壳的外表面进行削平处理，并选用梯形压电陶瓷片以增大压电陶瓷片的面积。压电陶瓷片的极化方向如图5所示，两片相对的压电陶瓷片的极化方向相同。

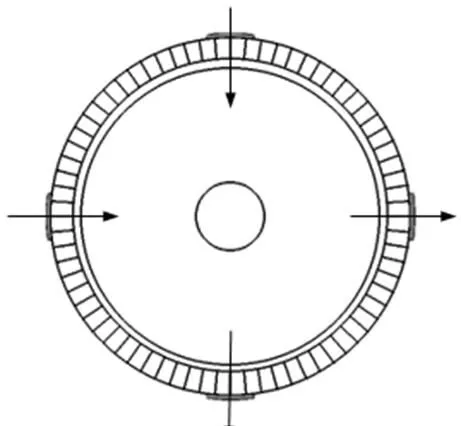
图5 陶瓷片极化方向

4 结论

提出了一种形状新颖锥壳形旋转行波超声电机，解决了面内弯曲与面外弯曲旋转行波超声电机的问题。锥壳形超声电机的转子为实体圆锥，可以将定子激发出的耦合模态充分利用。利用ANSYS软件对振子形状进行设计及模态分析，在锥壳的多个弯曲模态中选择了三阶弯曲模态为工作模态，得到了锥壳形振子的固有频率为25 954.6 Hz。

确定了振子的尺寸参数，明确了梯形陶瓷片的布置方式和极化方向，为锥壳形超声电机的后续研究奠定了基础。

[1] 赵淳生. 超声电机技术与应用[M]. 北京: 科学出版社, 2007.

[2] 康国华, 周琼峰, 范凯, 等. 采用超声电机的旋转式惯导系统转台[J]. 中国惯性技术学报, 2016, 24(4): 421-426.

[3] 梁大志, 时运来, 朱华, 等. 超声电机驱动及控制技术的新进展[J]. 振动、测试与诊断, 2012, 32(6): 990-993, 1039.

[4] 安大伟, 张建辉, 薛昊东, 等. 旋转行波超声电机性能提升技术进展[J]. 光学精密工程, 2020, 28(5): 1109-1115.

[5] Zhang J , Yang L , Ma C , et al. Improving efficiency of traveling wave rotary ultrasonic motor by optimizing stator. [J]. The Review of scientific instruments, 2019, 90(5): 56-64.

[6] 王楠, 陈超, 陈金燕. 一种圆筒型转子的中空型超声电机的研制[J]. 压电与声光, 2019, 41(02): 203-206.

[7] Bekiroglu E. Ultrasonic motors: Their models, drives, controls and applications[J]. Journal of electroceramics, 2008, 20(3): 277-286.

[8] 羊全钢, 张凯, 周铁英, 等. 弯曲旋转超声电机接触界面锥形角的分析与实验[J]. 声学学报, 2002(5): 413-419.

[9] 李英华, 何勍. 含齿环形振子的振型一致性分析[J]. 辽宁工业大学学报：自然科学版, 2011, 31(2): 132-134.

Structure Design and Modal Analysis of a Cone-shell Rotating Ultrasonic Motor

ZHAO Yan-dong, HE Qing, YU Xiang-rui

（College of Mechanical Engineering and Automation, Liaoning University of Technology, Jinzhou 121001, China）

In order to solve the problem of the difficulty in stable contact between the rotor of the in-plane curved rotating traveling wave motor and the vibrator and the problem of the rotor radial slip when the out-of-plane curved rotating traveling wave motor is running, a cone-shell-shaped rotating traveling wave ultrasonic motor is proposed. The conical ultrasonic motor vibrator and the rotor are in conical surface contact, which can couple in-plane vibration with out-of-plane vibration. The finite element software is used to establish the working mode, natural frequency and structural size of the vibrator, which lays the foundation for the follow-up research on cone ultrasonic motor.

cone-shell; ultrasonic motor; rotary traveling wave; modalanalysis

10.15916/j.issn1674-3261.2021.05.005

TB535；TM356

A

1674-3261(2021)05-0301-03

2020-12-23

赵彦东(1995-)，男，辽宁朝阳人，硕士生。

何 勍(1962-)，男，吉林东丰人，教授，博士。

责任编辑：陈 明