代价树深度优先搜索及优化

刘庆宇

代价树深度优先搜索及优化

刘庆宇

（辽宁工业大学 电子与信息工程学院，辽宁 锦州 121001）

代价树深度优先搜索算法是代价树搜索的常用方法之一，但在没有限制条件的情况下，可能陷入死循环或者大量无效搜索，存在搜索不完备以及所找的解未必是最优解的问题。针对深度优先搜索的缺点，在搜索过程中设计一定的剪枝条件，以提高搜索效率避免陷入死循环，并尽量返回代价更低的解。

代价树；搜索；深度优先

搜索是人工智能学科重要的研究内容之一，指从当前状态出发，根据一定的条件及规则搜索到达目标状态路径的过程，包括盲目搜索和启发式搜索[1]。其中盲目搜索指在搜索中每一步都根据既定的规则和策略进行搜索，启发式搜索则是指在搜索过程中的每一步都根据估价函数或一定的方法选择离目标状态预测更优的路径继续搜索[2]。

代价树是代价搜索树的简称，指有向边上标有代价(或花费)的搜索树。代价树的搜索与普通搜索的区别在于搜索过程中要考虑当前搜索路径代价并选择较低代价的路径继续搜索[3]。

1 代价树深度优先搜索算法

1.1 算法介绍

代价树的深度优先搜索主要是从根节点S0开始进行扩展，并从后继节点中选择代价最小的节点继续扩展，并以此类推，直到节点无法扩展且没有找到解时进行回溯，若找到解，则返回。

代价树深度优先搜索需要定义2个队列，OPEN队列代表未扩展节点的队列，CLOSED队列代表已扩展节点的队列。

定义节点j的代价f(j) = f(i) + c(i,j)，其中c(i,j)代表边节点i到其后继节点j的代价。

算法的流程如下。

(1)将节点S0放入OPEN表中，CLOSED表置空。

(2)判断OPEN表是否为空，若空则返回，若不为空则从OPEN表的首部拿出第一个节点n放入CLOSED表中。

(3)判断节点n是否目标节点，若是，则返回。

(4)判断节点n是否可扩展，若不可扩展，则返回步骤(2)。

(5)若节点n可扩展，则对节点n进行扩展，计算后继节点代价并按从小到大的顺序排序后加入到OPEN表的首部，返回步骤(2)。

1.2 算法缺点分析

(1)算法在对节点进行扩展时，没有考虑后继节点是否在祖先节点中出现过，导致可能出现死循环。

(2)算法在扩展节点时没有考虑该节点是否是已搜索过的无效节点。

(3)算法在执行复杂搜索时由于没有限制条件导致可能在无解路线上浪费大量时间。

(4)算法返回的搜索结果不一定是最优解。

2 代价树深度优先搜索优化

2.1 算法优化

针对代价树深度优先搜索的缺点，对算法进行相应改进。

(1)根据具体问题对深度优先搜索算法进行搜索层数限制，当搜索达到规定的层数后，即视为无法扩展。若搜索完毕后依然没有找到解，则提高限制层数。

(2)对节点n进行扩展时，判断其是否出现在CLOSED表中，若存在则丢弃节点n。

(3)对节点n进行扩展时，判断相应的后继节点是否出现在OPEN表中，若存在则比较其代价，若后继节点代价低则丢弃OPEN表中的相应节点，若节点n后继节点代价高则丢弃相应的后继节点。

2.2 改进算法应用分析

推销员旅行问题，设有7个城市A、B、C、D、E、F、G，交通路线如图1所示，图中数字代表所需路费，推销员要从A城市到达G城市，怎么样去搜索一条花费更低的路线？

2.2.1 深度优先搜索过程

按照深度优先搜索方法，遍历顺序如图2所示。

(1)首先从节点A出发扩展，将节点B、节点C加入OPEN表中，将节点A加入CLOSED表中。

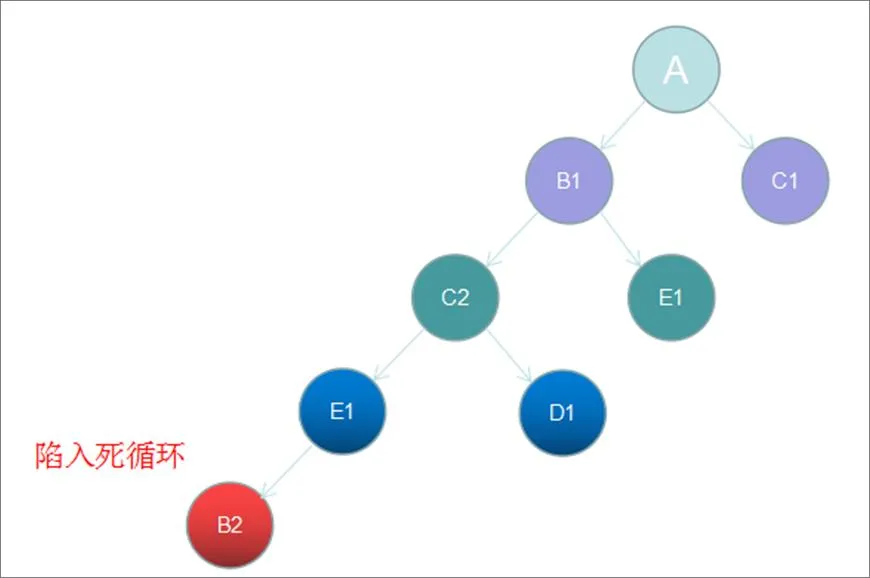
图2 深度优先搜索过程

(2)选择代价更小的B节点扩展，从OPEN表中取出节点B并将节点B加入CLOSED表中，扩展节点B，将节点C、节点E加入OPEN表中。

(3)选择代价更小的C节点扩展，从OPEN表中取出节点C并将节点C加入CLOSED表中，扩展节点C，将节点E、节点D加入OPEN表中。

(4)选择代价更小的E节点扩展，从OPEN表中取出节点E并将节点E加入CLOSED表中，扩展节点E，此时后继节点中B为代价最小的节点，搜索将会陷入死循环。

2.2.2 改进深度优先搜索过程

因城市数量较少，可以不通过设置层数限制搜索深度，按照改进的深度优先搜索方法，遍历顺序如图3所示。

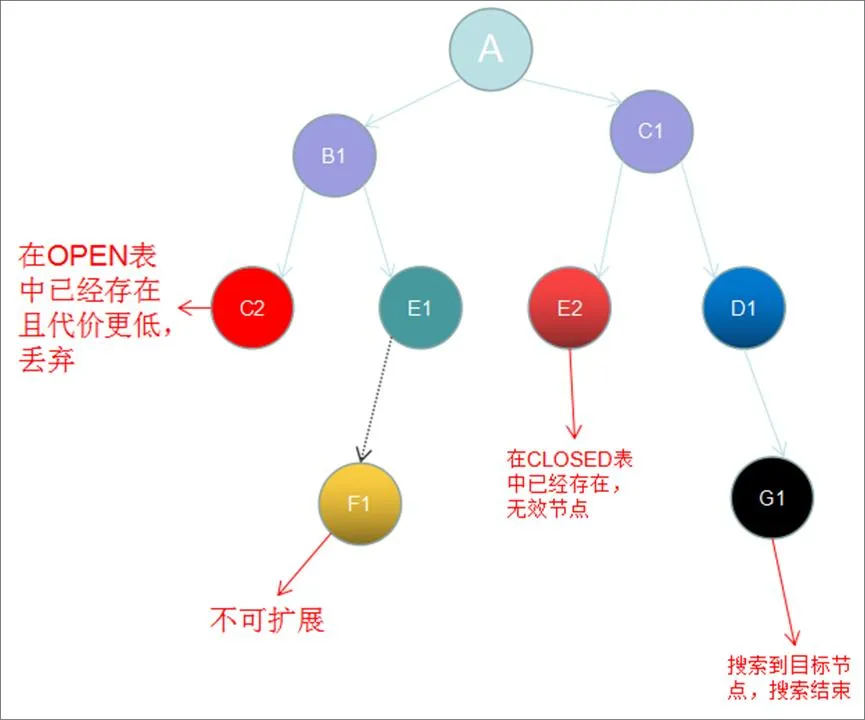
图3 改进深度优先搜索过程

(1)首先从节点A出发扩展，将节点B、节点C加入OPEN表中，将节点A加入CLOSED表中。

(2)选择代价更小的B节点扩展，从OPEN表中取出节点B并将节点B加入CLOSED表中，扩展节点B，因节点C已经在OPEN表中存在且原节点代价更小故丢弃，将节点E加入OPEN表中。

(3)选择节点E扩展，从OPEN表中取出节点E并将节点E加入CLOSED表中，扩展节点E，将节点F加入OPEN表中。

(4)选择节点F扩展，从OPEN表中取出节点F并将节点F加入CLOSED表中，扩展节点F，节点F不可扩展。

(5)选择节点C扩展，从OPEN表中取出节点C并将节点C加入CLOSED表中，扩展节点C，将节点E和D加入OPEN表中。

(6)选择节点E扩展，因节点E在CLOSED表中已经存在，是无效节点，故丢弃。

(7)选择节点D扩展，找到解，搜索结束。

3 结语

经过推销员旅行问题的验证，改进后的算法避免了搜索陷入死循环，提高了搜索效率。但依然存在找到的解未必是最优解的问题，搜索到的解相比普通深度优先搜索更优。

[1] Lu Kai, Tang Tao, Gao Chunhai. The Depth-First Optimal Strategy Path Generation Algorithm for Passengers in a Metro Network[J]. Sustainability, 2020, 12(13): 1-16.

[2] 龚建华. 深度优先搜索算法及其改进[J]. 现代电子技术, 2007(22): 90-92.

[3] 张建旭, 蒋燕, 刘兴国. 基于深度优先反向搜索算法确定有效路径集合[J]. 重庆交通大学学报: 自然科学版, 2015, 34(3): 93-98.

Depth First Search for Cost Tree and Its Optimization

LIU Qing-yu

（School of Electronics & Information Engineering, Liaoning University of Technology, Jinzhou 121001, China）

The depth first search algorithm for cost tree is one of the common methods of cost tree search. It may fall into an endless loop or a large number of invalid searches in the case of no constraints. The depth first search may be not complete and the solution may be not optimal. Aiming to solve the shortcomings of depth first search, some pruning conditions are designed in the search process to improve the search efficiency and avoid falling into the dead loop and return the solution with lower.

cost tree; search; depth first

10.15916/j.issn1674-3261.2021.05.010

TP301.6

A

1674-3261(2021)05-0322-03

2020-12-15

刘庆宇(1991-)，男，辽宁康平人，讲师，硕士。

责任编辑：孙 林