改进蚁群算法对TSK-FLS的参数设计

兰 洁

改进蚁群算法对TSK-FLS的参数设计

兰 洁

（辽宁工业大学 理学院，辽宁 锦州 121001）

模糊逻辑系统(FLS)是被证实行之有效的估计器，有其他系统不可比拟的优越性，但存在着参数选取以及规则数等难以获取的缺点。蚁群算法(ACO)是一种基于局部更新信息素搜索寻优的策略，在此算法基础上改进全局信息素更新设计改进蚁群算法(IACO)。它不仅继承蚁群算法可以解决随机择路的复杂优化问题，同时克服候选解随机搜索空间大，反复迭代效率低的缺点。将此改进的优化蚁群算法用于TSK-FLS的参数调整和规则筛选，设计一种智能优化的模糊逻辑系统，并将改进蚁群算法优化后的模糊逻辑系统应用于国际油价预测。通过数值预测仿真结果以及对比结果可以看出，该改进算法在TSK-FLS的参数设计的有效性和可靠性，并缩小了传统蚁群算法的搜索空间并提高计算效率。

改进ACO；TSK-FLS；参数设计

模糊逻辑系统能够基于逻辑和主观经验对信息进行感知和决策，广泛应用于人工智能控制、图像处理、语言识别、智能决策等前沿领域。模糊逻辑系统设计中最重要部分是基于模糊规则以及系统参数的模糊推理机，规则数筛选以及系统参数的获取是一个重要问题[1]。反向传播(BP)算法设计可将系统分解的低阶子系统，通过设计虚拟控制，反推到整个系统的控制性能实现规则的筛选及参数选取，但只能实现局部收敛；最小二乘法广泛用于已有测量数据来估计未知参数解决构造模型最优解问题，但存在选取粗糙很难实现精准设计需求。模糊逻辑系统在人工智能领域的重要位置，利用智能算法[2]的高性能和全局收敛性，使得应用智能算法优化模糊逻辑系统设计受到越来越多学者的密切关注和研究。目前已经有许多算法被用于模糊逻辑系统的优化设计，如蚁群、蜂群、粒子群[3]、遗传算法[4]等。

蚁群算法[5]是一种源于自然界仿生的分布式随机正反馈搜索算法。通过对候选解的组成群体进行随机优化来寻求最优解，从而逐渐实现全局最优。随机搜索算法在扩大搜索范围以及提高算法效率之间存在矛盾，因此产生了一些改进算法，如精英蚁群策略[6]、最大-最小蚂蚁系统、排序蚁群系统。精英蚁群策略和基于测序的蚁群系统都侧重减少搜索空间。不同之处在于，精英蚁群策略是一种格外强化当前最优解路径选择，用指数幂强化此路径信息素，进一步迭代出最短路径；排序蚁群系统将每次迭代产生的路径降序排列，并赋予降序权重。但这2种算法的效率并没有提高，很可能陷入局部最优解，从而系统停滞，不再继续迭代搜索最优解。通过设置信息素大小值的最大-最小蚁群算法虽然可以有效解决局部最优解问题，但并不能显著提高算法的效率。

基于算法存在问题的进一步研究，构建一种利用全局信息素更新的改进蚁群算法，可有效压缩搜索空间并可以提升算法效率。模糊逻辑系统因其良好的估计特性受到控制领域的广泛应用[7-9]，特别是一型FLS针对未知的非线性的估计。将此进化搜索改进优化蚁群智能算法使用在对TSK-FLS的参数调整和规则筛选具有很广泛的实际意义，并进一步将此算法对国际油价的数值仿真预测，证实了该算法的有效性。

1 利用改进算法筛选规则及选定参数

2.1 蚁群路径选择

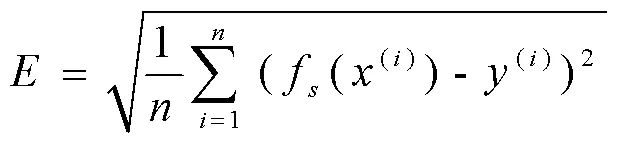
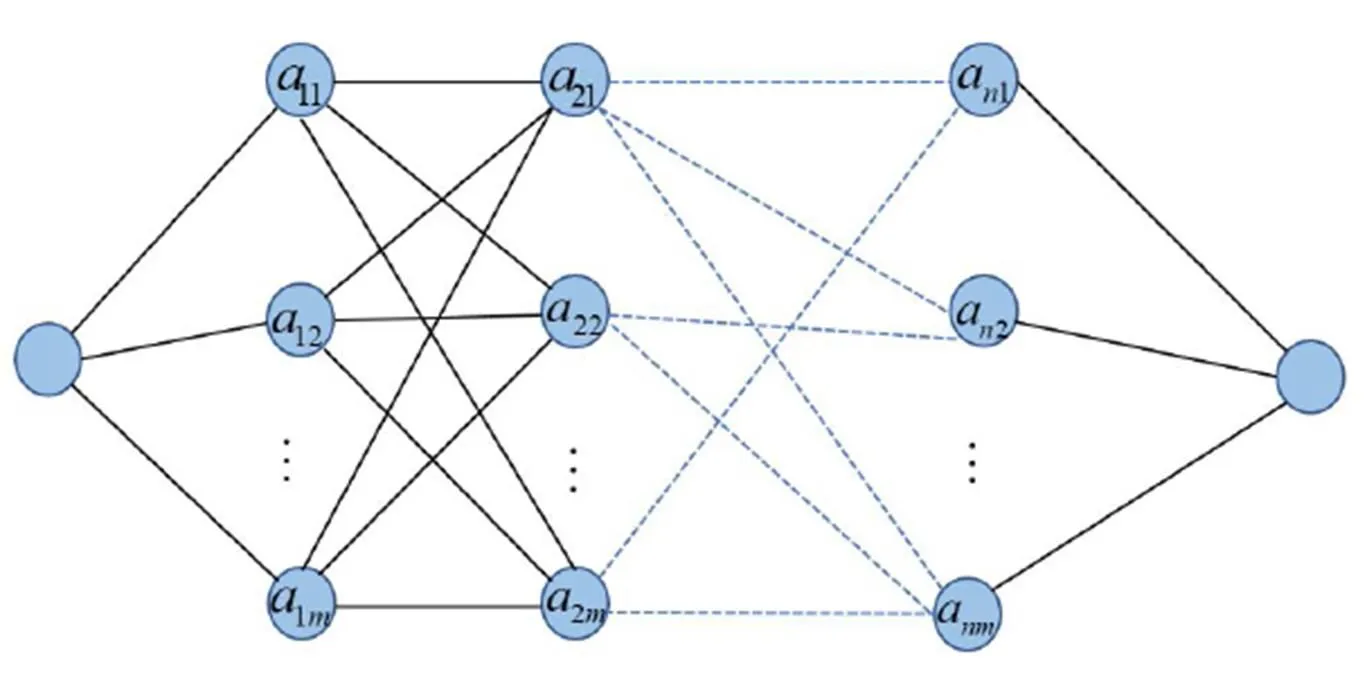
图1 模糊神经网络路径图

其次，随机分配只蚂蚁到每个节点处，并建立对应的禁忌表，以防止蚂蚁重复访问同一节点，过早陷入局部最优解；蚂蚁根据式(2)计算的概率选择下一个访问的节点。蚂蚁携带一定浓度量的信息素，并在经过的路径上遗留信息素。蚂蚁会依据所感知的信息素浓度判定下一步行动路径，一般会选择信息素浓度高的方向，进一步强化该路径的选择以及信息素浓度。

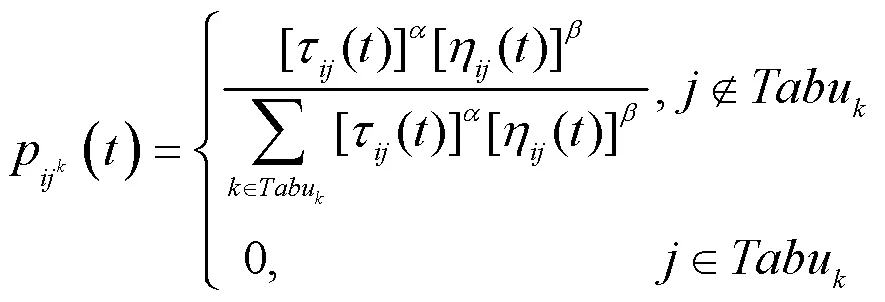
2 更新信息素的迹

2.1 局部更新

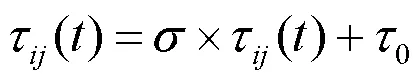
其中，表示蚂蚁所携带的信息素总量，E表示蚂蚁访问过的节点构成的TSK-FLS的均方根误差RMSE。

2.2 全局信息素的迹的更新

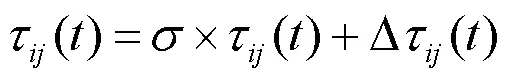
其中，E表示局部参数最优时刻的均方根误差。

该算法具有以下优点：(1)全局信息更新时只对当前最优路径信息的迹更新，迹越多浓度越大，蚂群访问的概率就越大，从而缩小了蚁群的搜索空间；(2)最优路径信息素的迹增加越快，越吸引蚁群逼近最优路径，从而更新全局信息素迹，增加算法收敛的速度。

设置3种情况为改进算法的结束条件：(1)设置终止迭代次数，运行到此迭代次数结束运算；

(2)设置误差，满足误差条件，结束运算；(3)最优路径的选取不再发生变化，算法已实现收敛时，算法结束。

3 改进蚁群算法对TSK-FLS的参数选取与规则筛选

3.1 TSK-FLS结构

在本文中TSK-FLS：单点模糊化，多输入单输出的模糊规则库，构建高斯型隶属函数的乘积范数下的模糊推理机，利用中心降型解模糊化这4部分构成的系统[15]。TSK-FLS的第条规则：

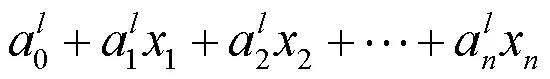
将模糊逻辑系统设计成网层结构，构建一个5层的模糊神经网络系统。

第一层：输入层，将规则数以及参数选取作为输入。

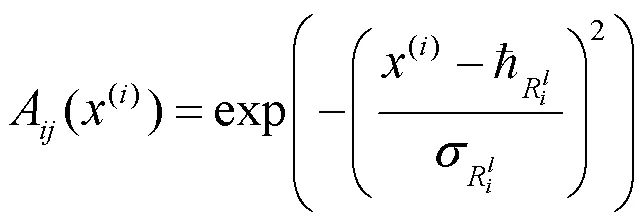
第四层：权重层，计算每条规则的权重：

第五层：输出层，输出为：

3.2 参数调整和规则筛选的步骤

(1)利用BP算法，求出可能候选参数及规则数生成路径的最大值和最小值。按照图1构造蚂蚁搜索路径图和路径矩阵。

(2)定义变量。随机分配蚂蚁在各个节点，在TSK-FLS中蚂蚁指的是参数及规则，并且构建相应的禁忌表，防止重复访问同一节点。

(4)当所有蚂蚁访问每个节点时，根据式(4)更新全局信息素，并找出当前最优参数和规则选取，计算由最优参数组成的RMSE。

(5)清空禁忌表，在循环数上加1，根据以上3种方法中的任何一种结束算法。

(6)输出结果。

4 应用实例

设计国际油价的数值预测，选取248个数据，采用前件124个数据进行参数训练，后件124个数据用于系统测试。改进蚁群算法对模糊逻辑系统的规则参数选取，采用输入训练对进行预测，3个数据预测下一个数据的方式。设计TSK模糊逻辑系统，对于规则的每一个前件取2个模糊集，这样就有23=8个模糊规则。模糊规则形式如下：

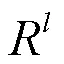
运用改进蚁群算法对模糊逻辑系统的参数和规则调节，因为后件有4个待调节的参数，总共有8条规则，这样就有32个待调节参数，也就是需要找出32个最优参数，这样需要构造一个32×32维的路径矩阵。这里设置路径矩阵是一个对称的无向图，并且规定自身和自身距离为零。每个参数等分为最大值和最小值之间的15个值，共有32×15=480个待选参数。通过BP算法分别得到每个参数的最大值和最小值，初始参数选取如下：

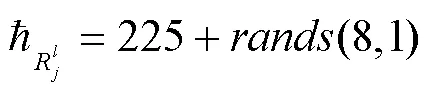
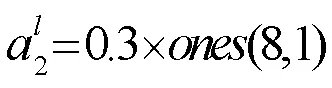
通过对前件124个数据训练，对TSK-FLS中的参数和规则选取，优化参数选取后的预测结果如图2所示，可以看出，经过数据训练改进蚁群算法对TSK-FLS的预测模型与实际输出拟合效果较好，预测是比较可行、有效。

图3中，后件的124个数据用于测试系统预测国际石油走势效果，可以看出测试数据取得了理想的预测效果，展示了很好的数据拟合结果。图4中，最小二乘法，改进蚁群算法与样本数据值进行比较，可以看出改进算法预测效果与测试数据的图像拟合效果更好，相对误差更小。

为了验证利用全局信息素更新优化后的蚁群算法具有更好的性能(图5)，在进一步数据仿真中设置100次迭代，通过对TSK-FLS参数设计的预测效果的比较可以看出更新全局信息素的改进蚁群算法筛选规则和参数确定的TSK-FLS在预测上面有更好的性能。

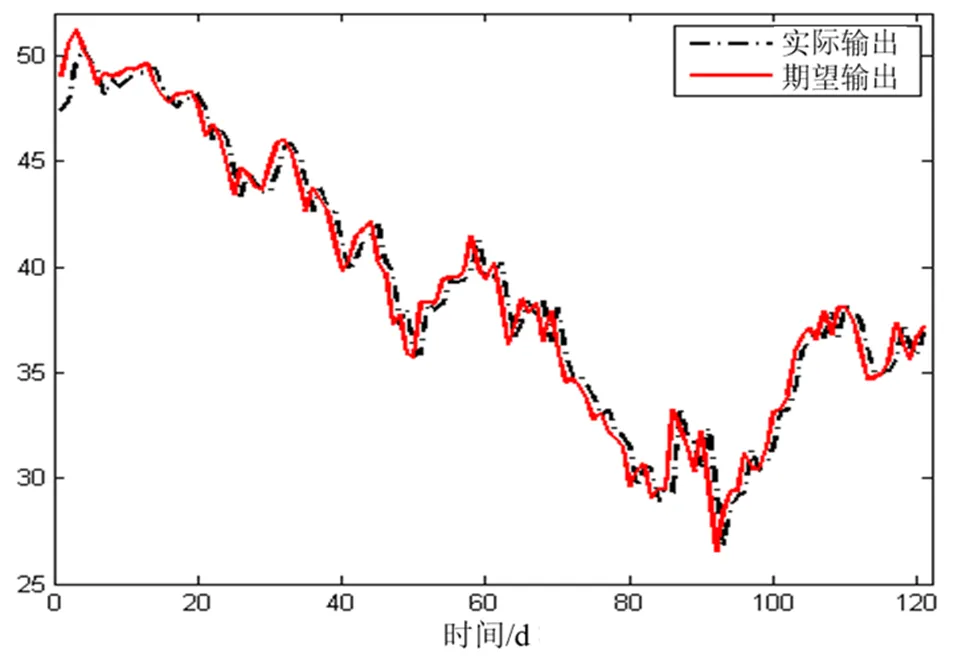
图2 改进蚁群对TSK-FLS参数优化训练

图3 测试预测国际石油走势效果图

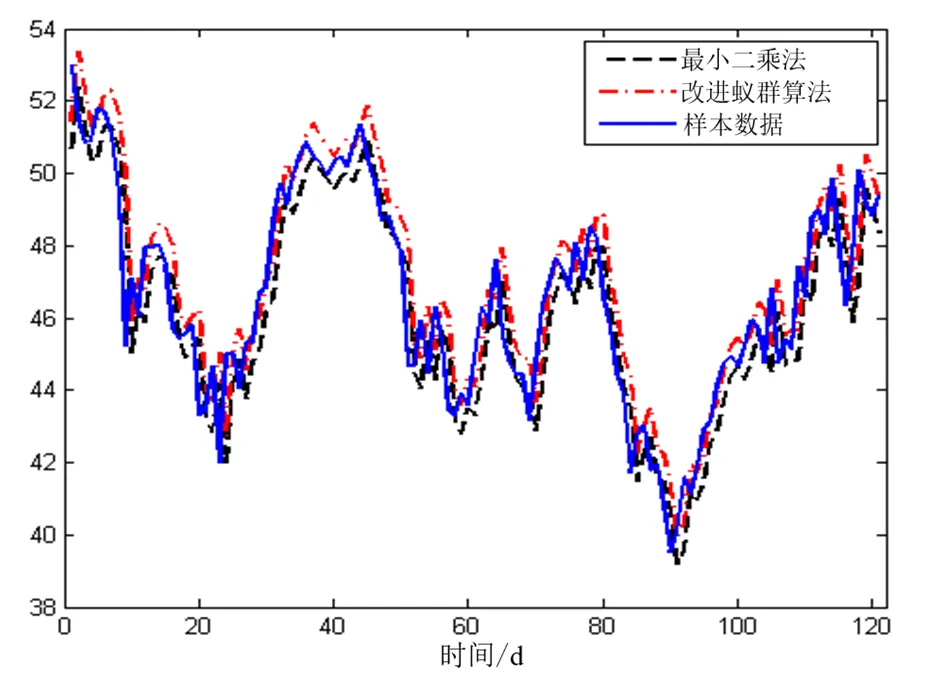
图4 比较改进蚁群算法与经典算法的预测效果

设置迭代次数为100，不同算法下设计的TSK-FLS预测的均方根误差RMSE结果如表1。蚁群算法下FLS的预测输出误差是1.42，改进蚁群算法下的FLS的预测输出误差是1.28，都小于最小二乘法的预测误差1.57；进一步表明该改进算法缩小随机搜索空间，预测效果可更快接近设置误差，同时也说明仿生进化式搜索寻优算法比传统的经典算法具有更高的精度性能。

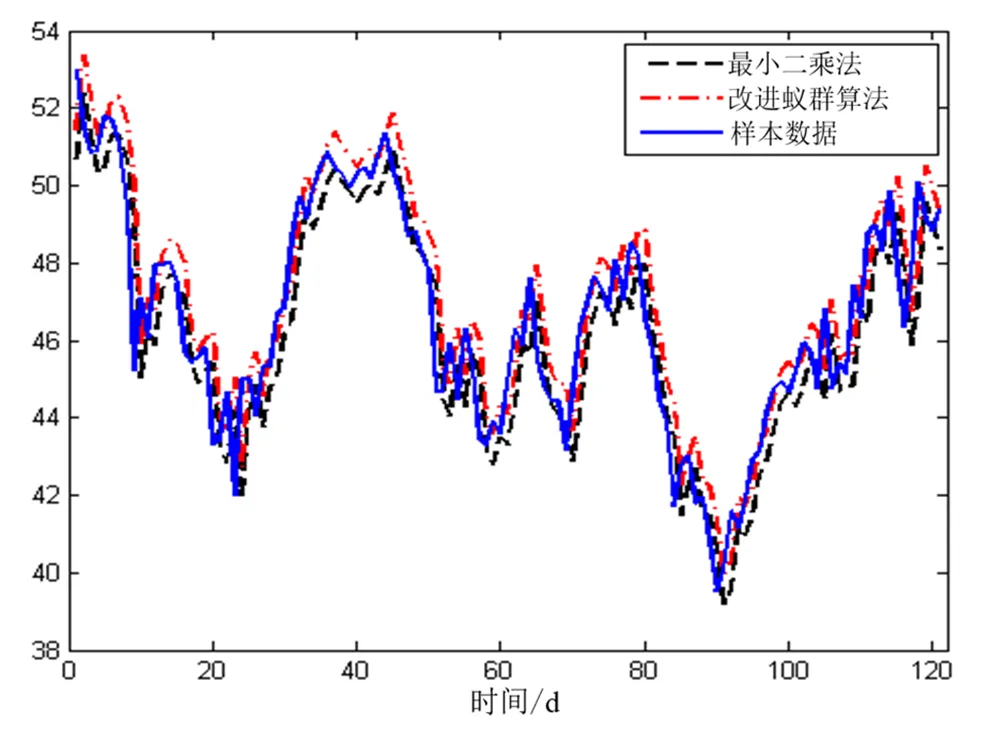
图5 比较改进蚁群与经典蚁群的预测效果

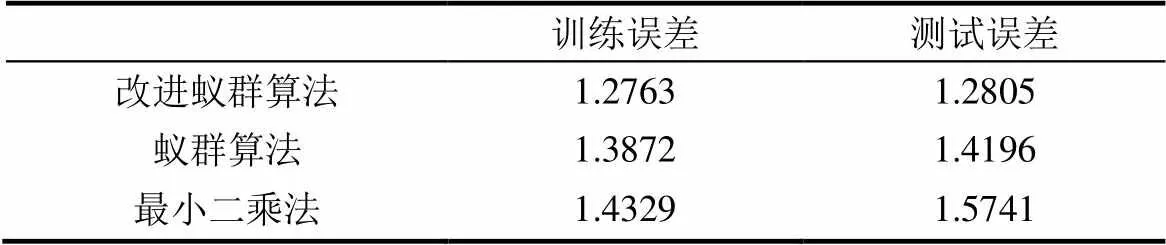
表1 算法预测的RMSE

5 结论

应用TSK-FLS，利用进化算法优化系统中参数选取以及规则筛选，不但可以通过候选解寻求最优解处理参数设计问题，还进一步解决蚁群算法的随机搜索中的空间较大、效率较低的缺点，并将此优化后的模糊逻辑系统预测国际油价。数值仿真的结果说明，改进的TSK-FLS模型预测具有更好的效果，可以有效提高优化算法的效率，尤其针对系统中具有不确定的非线性的智能控制器设计，具有较强的鲁棒性，进一步可用于多重目标决策和多目标控制等问题，特别是针对多智能体编队控制中优化路径规划，提高轨迹跟踪，对避障避撞有一定的应用前景，可以进一步探索。

[1] Juang C F, Lo C. Fuzzy systems design by clustering-aided ant colony optimization for plant control[J]. International Journal of General Systems, Dec. 2007, 36(6): 623-641.

[2] Takagi T, Sugeno M. Fuzzy identification of systems and its applications to modeling and control[J]. IEEE transactions on systems, man, and cybernetics, 1985(1): 116-132.

[3] Juang C F, Hung C W, Hsu C H. Rule-based cooperative continuous ant colony optimization to improve the accuracy of fuzzy system design[J]. IEEE Transaction on Fuzzy Systems, 2014, 22(4): 723-735.

[4] Dorigo M, Birattari M, Stutzle T. Ant colony optimization [J]. IEEE Computational Intelligence Magazine, 2006, 1(4): 28-39.

[5] Sim K M, Sun W H. Ant colony optimization for routing and load-balancing: survey and new directions[J]. IEEE Transactions on Systems, Man, and Cybernetics-Part A: Systems and Humans, 2003, 33(5): 560-572.

[6] Socha K, Dorigo M. Ant colony optimization for continuous domains[J]. European Journal of Operational Research, 2008, 185(3): 1155-1173.

[7] Yu J P, Zhao L, Yu H S, et al. Fuzzy finite-time command filtered control of nonlinear systems with input saturation[J]. IEEE Transactions on Cybernetics, 2018, 48(8): 2378-2387.

[8] Wang M, Chen B, Liu X P, et al. Adaptive fuzzy tracking control for a class of perturbed strict-feedback nonlinear time-delay systems[J]. Fuzzy Sets and Systems, 2008, 159(8): 949-967.

[9] Lan J, Liu Y J, Liu L, et al. Adaptive output feedback tracking control for a class of nonlinear time-varying state constrained systems with fuzzy dead-zone input[J]. IEEE Transactions on Fuzzy Systems, 2021, 29(7): 1841-1852.

[10] Juang C F, Chang P H. Designing fuzzy-rule-based systems using continuous ant-colony optimization[J]. IEEE Transactions on Fuzzy Systems, 2009, 18(1): 138-149.

[11] Ma X J, Sun Z Q, He Y Y. Analysis and design of fuzzy controller and fuzzy observer[J]. IEEE Transactions on Fuzzy Systems, 1998, 6(1): 41-51.

[12] Yuan X, Zhang C, Ren Y. Generalized fuzzy groups and many-valued implications[J]. Fuzzy Sets and Systems, 2003, 138(1): 205-211.

[13] Castillo O, Lizárraga E, Soria J, et al. New approach using ant colony optimization with ant set partition for fuzzy control design applied to the ball and beam system[J]. Information Sciences, 2015, 294: 203-215.

[14] Bououden S, Chadli M, Karimi H R. An ant colony optimization-based fuzzy predictive control approach for nonlinear processes[J]. Information Sciences, 2015, 299: 143-158.

[15] Mendel J M. General type-2 fuzzy logic systems made simple: a tutorial[J]. IEEE Transactions on Fuzzy Systems, 2013, 22(5): 1162-1182.

Improved Ant Colony Algorithm for TSK-FLS Parameter Design

LAN Jie

（College of Science, Liaoning University of Technology, Jinzhou 121001, China）

Fuzzy logic system (FLS) is proved to be an effective estimator, but it has some disadvantages such as parameter selection and rule number difficult to obtain. Ant Colony Algorithm (ACO) is an optimization strategy based on local update pheromone search. Based on this algorithm, the global pheromone update design, improved ant colony algorithm (IACO) is improved. The method inherits the advantages of ant colony algorithm to solve the complex optimization problem of random routing, but also overcome the shortcoming of large random search space and low repeated iteration efficiency of candidate solutions. The improved ant colony algorithm is applied to the parameter adjustment and rule selection of TSK-FLS, and an intelligent and optimized fuzzy logic system is designed. Further, TSK- FLS optimized parameters by IACO is applied to the international oil price prediction. Through data simulation results and comparison results, it can be seen that the improved algorithm is effective and reliable in the parameter design of TSK-FLS, and can reduce the search space of traditional ant colony algorithm and improve computational efficiency.

IACO; TSK-FLS; parameter design

10.15916/j.issn1674-3261.2021.05.007

O159

A

1674-3261(2021)05-0307-05

2021-05-29

辽宁省教育厅科研基金(JJL202015407)

兰洁(1982-)，女，吉林长春人，讲师，硕士。

责任编辑：孙 林