面向工程应用的应力集中与应力奇异现象的有限元研究

高思远，赵旭东，李卫民，江国海

面向工程应用的应力集中与应力奇异现象的有限元研究

高思远1，赵旭东2，李卫民2，江国海2

（1. 锦州师范高等专科学校 机械电子工程系，辽宁 锦州 121001；2. 辽宁工业大学 机械工程与自动化学院，辽宁 锦州 121001）

首先针对应力集中与应力奇异现象产生的原因进行了分析与总结；对应力集中与应力奇异在有限元求解过程中的变化规律进行了研究。此外，对不同网格类型及尺寸对有限元求解精度的影响进行了分析。随后，对应力奇异与应力集中的区别进行了讨论。最后，就所研究的问题总结了工程上的处理对策。

有限元技术；应力集中；应力奇异；网格无关解校验

在现代化生产中，由于产品性能的不断提升所带来的工程问题也日趋复杂化，为了达到预期的性能目标，工程设计人员在产品还未生产之前就需要对产品的可靠性、安全性能以及经济价值有一个宏观的预估。

多数产品在研发过程中都需要进行静态、动态或多物理场的校核，在静力学分析中，常常被关注的问题莫过于要考虑产品在刚度、强度、稳定性与疲劳失效等方面的问题。同时，在基于有限元技术进行产品结构静力学校核过程中，由于产品自身结构原因，求解中极易出现应力集中与应力奇异现象，这是每一个从事产品开发的CAE从业人员都无法规避的技术问题。由于局部应力集中现象或奇异解的出现，就会使计算得到的结果偏离了真实解，通常经计算得到的应力结果不能应用于后续产品的疲劳性能评估[1]。近年来，国内外学者围绕板孔的应力集中及其失效问题，不同材料之间连接的应力集中问题等进行了相关研究[2-7]。

基于此，在国内外研究成果基础上，进一步认识并了解在有限元求解过程中，产品应力集中与应力奇异现象产生的原因、掌握其变化规律，在此基础上找到解决这一问题的有效方法，将有利于提高有限元技术在工程应用中的求解精度与可信度。

1 应力集中与应力奇异产生的原因

1.1 应力集中现象产生的原因

在产品设计过程中进行刚度与强度的校核是必不可少的设计过程，产品刚度校核主要是关注产品在承受外力作用下抵抗变形的能力，而强度的校核则是关注产品在承受外力作用下抵抗破坏的能力。当产品承受交变载荷时，产品是否具有良好的设计结构和足够的强度会对其使用寿命产生直接影响，因此，应力强度的计算是静强度和疲劳校核的基础。

通常机械零部件结构复杂多变，当零件结构上存在孔、凹槽、凸台或是含有缺口等特征时，由于零件在这些特征的截面处存在几何形状上的剧烈变化，将会导致这些特征的局部位置存在较高的应力，而这些较高应力的峰值则远远高于由理论公式所求得的应力值，出现这一现象时则认为产品结构上出现了应力集中的现象[8]。

1.2 应力奇异现象产生的原因

应力奇异主要是指由于受力件自身几何结构的影响，在求解应力函数时，出现了应力解发散的情况。导致求解过程中应力奇异现象出现的影响因素不一，基本是由于边界条件设置、集中载荷施加、模型光顺程度以及材料的光顺性等因素造成的[9]。

在实际问题中，任何一个构件都是存在一定强度的，并不可能存在无限大的应力值，并且零件在切削加工过程中，金属切削刀具的切削刃上均会存在圆弧，所以没有绝对的直角边。由此可知，在实际结构中应力奇异是不存在的，而这一现象的产生只会存在于数值计算中，其出现的主要原因在于模型的过度简化、实际外载的施加以及边界条件设置等方面存在问题，导致求解应力函数时出现了奇异解。奇异点的存在往往会导致有限元计算过程中解的收敛速度变慢。

应力奇异现象的产生最本质特征为：模型在有限元求解过程中，随着网格尺寸的不断变小，求解得到的应力却无限变大。由于求解模型的过度简化，对于直角过渡位置或是当载荷集中施加在某一点上时，在同等载荷作用下，受力面是一条没有面积的直线，由式(1)可知，当外载一定时，受力面积无限趋近于零，所得到的应力是趋近于无穷大的，而导致这一问题的出现的原因在于建立有限元模型时采用了理想化模型。

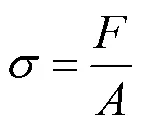
2 应力集中与应力奇异在有限元求解过程中的变化规律

2.1 分析模型的建立

因为应力集中和应力奇异与受力体结构及有限元求解过程中的离散程度有直接关系。所以，现以某简化的吊钩结构为研究对象，来探究其在有限元求解过程中位移与应力的变化规律，以及采用不同类型的求解单元对求解精度的影响，模型结构如图1所示。吊钩结构从用途上看为典型的受力件，模型中含有圆孔及大弧度曲面等几何要素，这在求解过程中对网格质量有较大要求，也便于研究不同网格尺寸在求解精度上的影响规律。同时，为了区分不同结构对于有限元结果的影响，仅在挂钩受力的关键位置加以区别，分为直角模型及圆角模型，如图1所示。

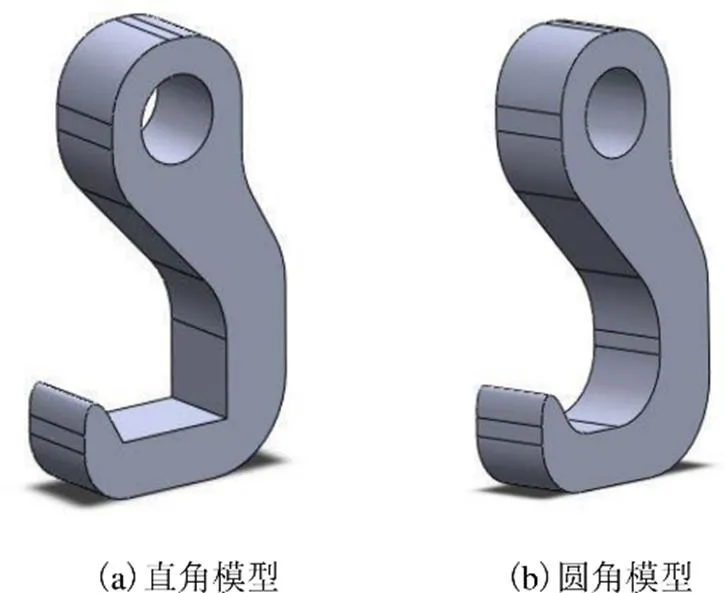
图1 用于有限元分析的模型图

定义吊钩材料为结构钢，在受力面施加一方向向下的静载荷，大小为10 000 N，并对上端圆孔施以固定约束。分别使用不同尺寸及类型的单元进行网格划分，网格类型为四面体高/低阶单元、六面体高/低阶单元；网格大小为1～20（单位: mm，增量为1），经静力学求解后对比其位移以及应力结果。

2.2 不同求解单元对直角模型应力位置及求解精度的影响

图2～图4分别为网格尺寸为20、12、2 mm下采用六面体高阶单元求得的直角模型的应力结果。观察求得的应力云图可以发现，随着网格尺寸不断加密，最大应力出现位置的不断靠近结构中的直角过渡位置(锐利的拐角位置)，由图2及图3观察可知，最大等效应力出现位置并未完全覆盖两层网格。当网格划分比较稀疏时，对于梯度变化较大的应力不易被捕捉到，最大等效应力值的大小及出现的位置是不准确的。

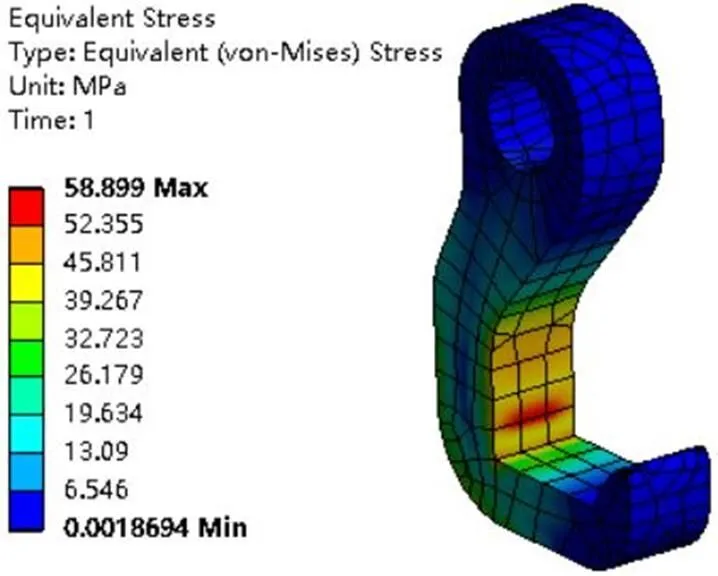
图2 网格尺寸为20 mm条件下的应力

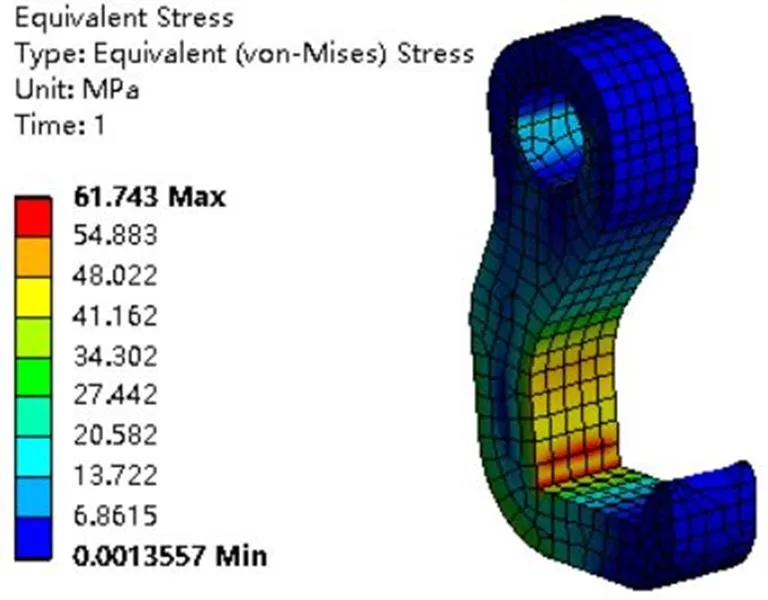
图3 网格尺寸为12 mm条件下的应力

图4 网格尺寸为2 mm条件下的应力

图5所示，为采用不同单元类型与尺寸求得的直角模型应力解的变化规律，由于直角模型在受力关键位置含有锐利的直边，在外载及边界条件不变的情况下，随着网格的不断加密，应力解逐渐变大，出现发散趋势，当网格尺寸细化到小于4 mm时，应力值出现了陡增，应力解出现了明显的发散现象。同时观察求解结果也可以发现在同等网格尺寸下，采用高阶单元所求解的应力值普遍高于低阶单元的求解结果，但是当网格细化到一定程度，高阶单元的发散趋势更为明显。

2.3 不同求解单元对直角模型位移求解精度影响

如图6所示，是采用不同单元类型与尺寸求得的直角模型的位移解的变化规律，从图中的变化规律可以看出采用高阶单元求得的位移解，在求解过程中位移受网格尺寸变化的影响不明显，具有良好的稳定性。当使用低阶单元进行求解时，无论是四面体单元还是六面体单元，受网格尺寸变化的影响较大，随着网格尺寸的不断加密，位移解逐渐趋于真实解。同时，当采用六面体低阶单元进行求解且网格划分的极为粗糙时，所求的位移解出现了较大程度的震荡，证明所求得的位移解存在较大误差。

图5 直角模型不同单元类型及网格尺寸下的应力解

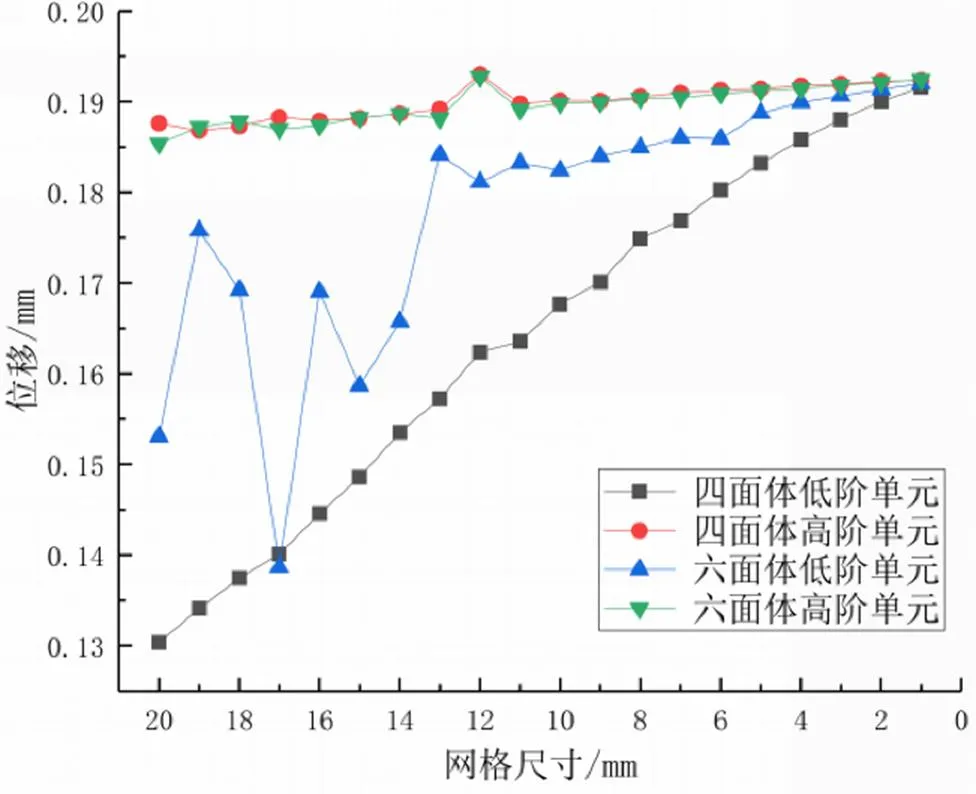
图6 直角模型不同单元类型及网格尺寸下的位移解

2.4 不同求解单元对圆直角模型应力位置及求解精度的影响

图7～图9分别为网格尺寸为19、5、1 mm下采用六面体高阶单元求得的圆角模型的应力结果。不论网格划分的粗细与否，最大应力的出现位置基本都在圆角附近。观察图7可知，由于网格划分的过于粗糙，最大等效应力并未均匀覆盖两层网格。因此，对于圆角结构当网格划分比较稀疏时，最大等效应力数值及出现的位置可靠度略低。但随着网格尺寸的不断加密，最大等效应力基本出现在圆角上，且数值相差不大。由图10观察可知，当网格尺寸细密到一定程度，最大等效应力解出现的位置及数值大小基本不再出现变化，表示最大等效应力数值的区域所覆盖的网格层数在不断增加，证明结果具有更高的可信度。

如图11所示，是采用不同单元类型与尺寸求得的圆角模型应力解的变化规律。

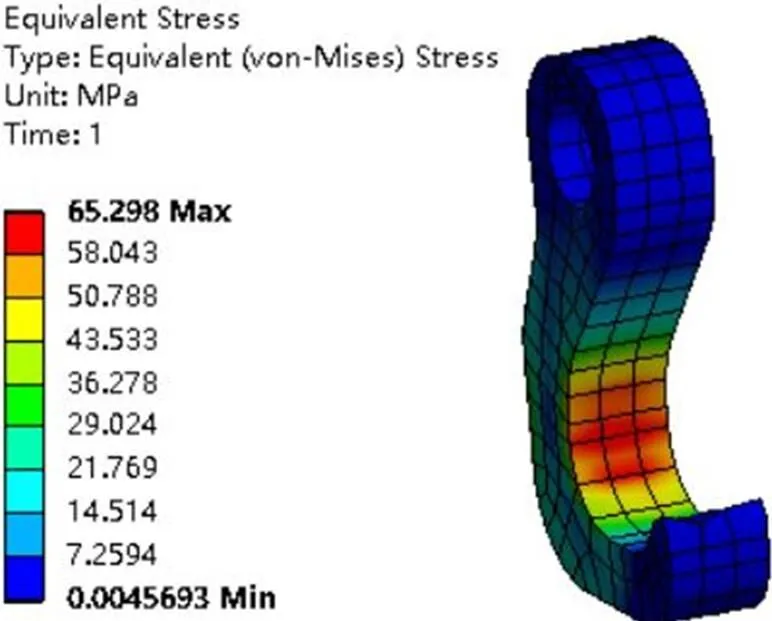
图7 网格尺寸为19 mm条件下的应力

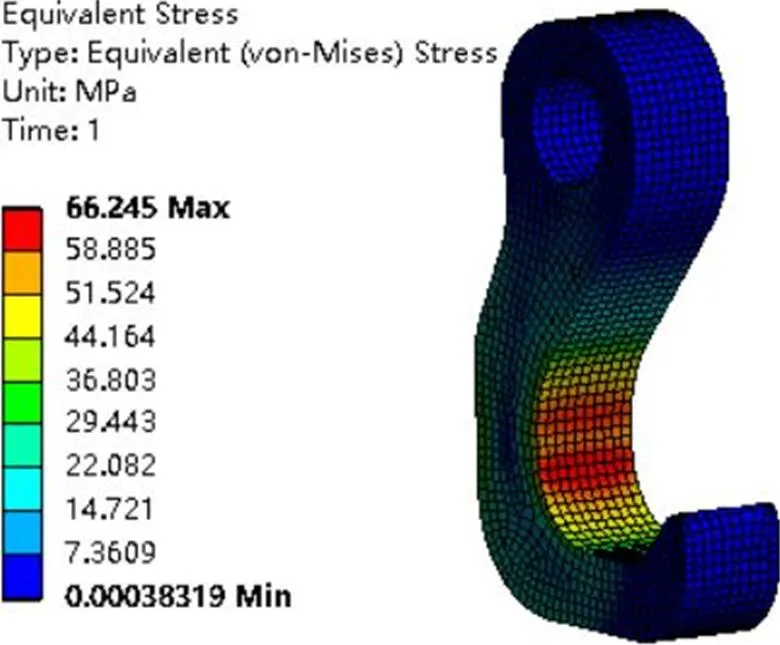
图8 网格尺寸为5 mm条件下的应力

图9 网格尺寸为1 mm条件下的应力

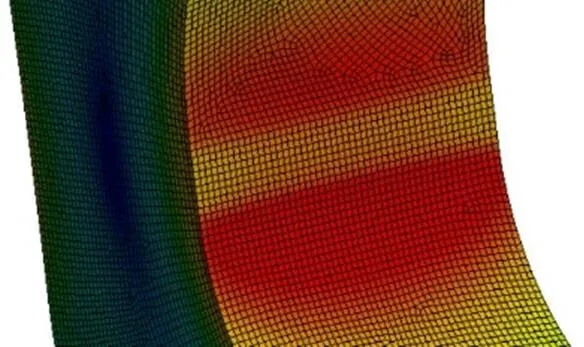
图10 网格尺寸为1 mm时的最大应力处局部放大图

可以看出，四面体高阶单元与六面体高阶单元所求结果较为吻合，整体趋势均不存在大幅度变化，应力解稳定，圆角结构具有良好收敛性。当网格尺寸细化到8 mm以下时，所求应力解几乎不变，收敛于66 MPa左右，高阶单元的求解精度均明显高于低阶单元。当采用四面体低阶单元进行求解时，由于网格划分过于粗糙，所求应力解出现了较大幅度变化，具有明显的求解误差。

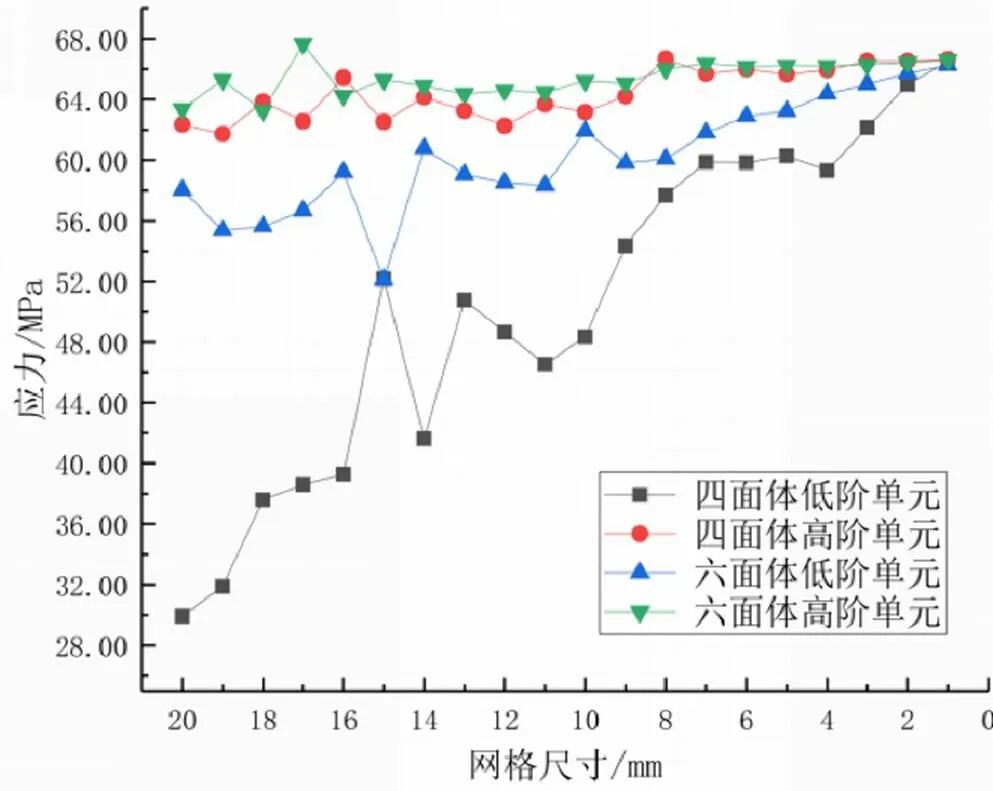
图11 圆角模型不同单元类型及网格尺寸下的应力解

2.5 不同求解单元对直角模型位移求解精度影响

如图12所示，圆角模型的位移解的变化规律与直角模型基本一致，但当采用高阶单元求解时位移解更为稳定，基本收敛于0.173 mm。

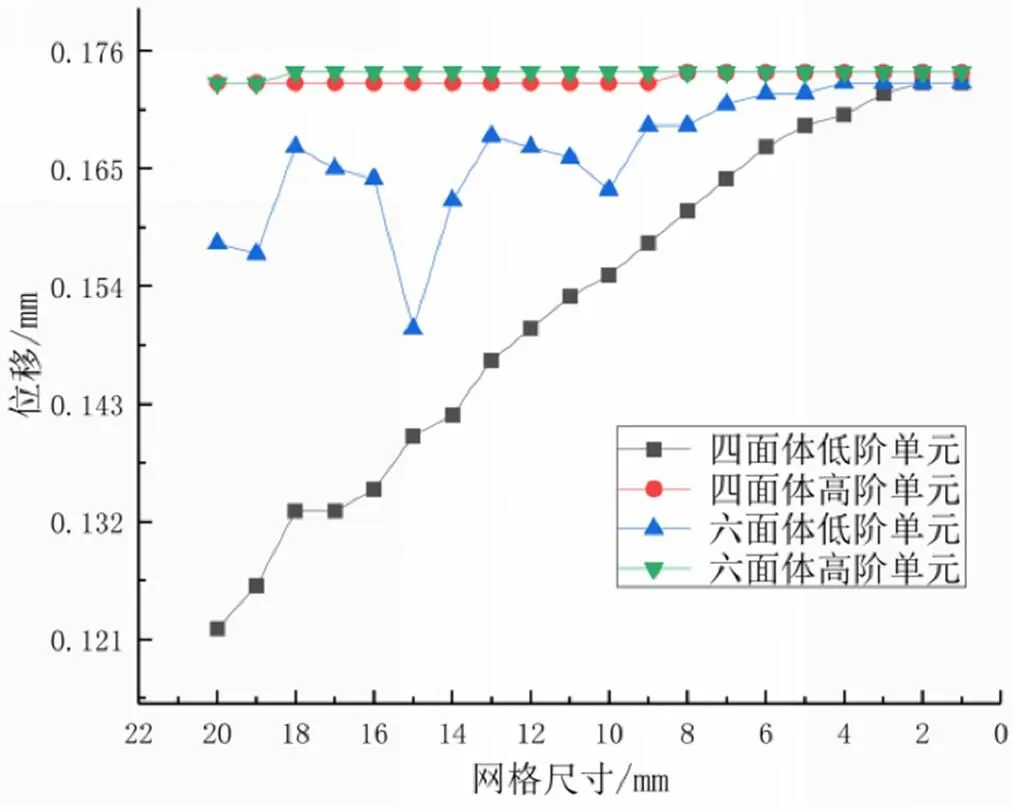
图12 圆角模型不同单元类型及网格尺寸下的位移解

2.6 不同求解单元对两类模型最大位移位置及求解精度的比较

观察图13的吊钩位移云图可知，无论是直角模型亦或是圆角模型，也无论网格尺寸划分的疏密与否，最大位移出现的位置相一致，均在挂钩受力面左侧远离固定约束位置的边缘处，位移解的数值大小变化幅度不大，基本相同，同时观察云图还可以看出，圆角结构相较于直角结构具有更高的刚度。此外，即使是直角模型中应力解存在应力奇异现象，但是其位移解与网格粗细程度无关，即使网格划分的较为粗糙，也可以获得具有一定可信度的位移解。因此，在工程中如果仅需要校核结构的刚度，可以采用较为稀疏的网格划分方法，在提高计算效率的基础上同样可以得到精确解。

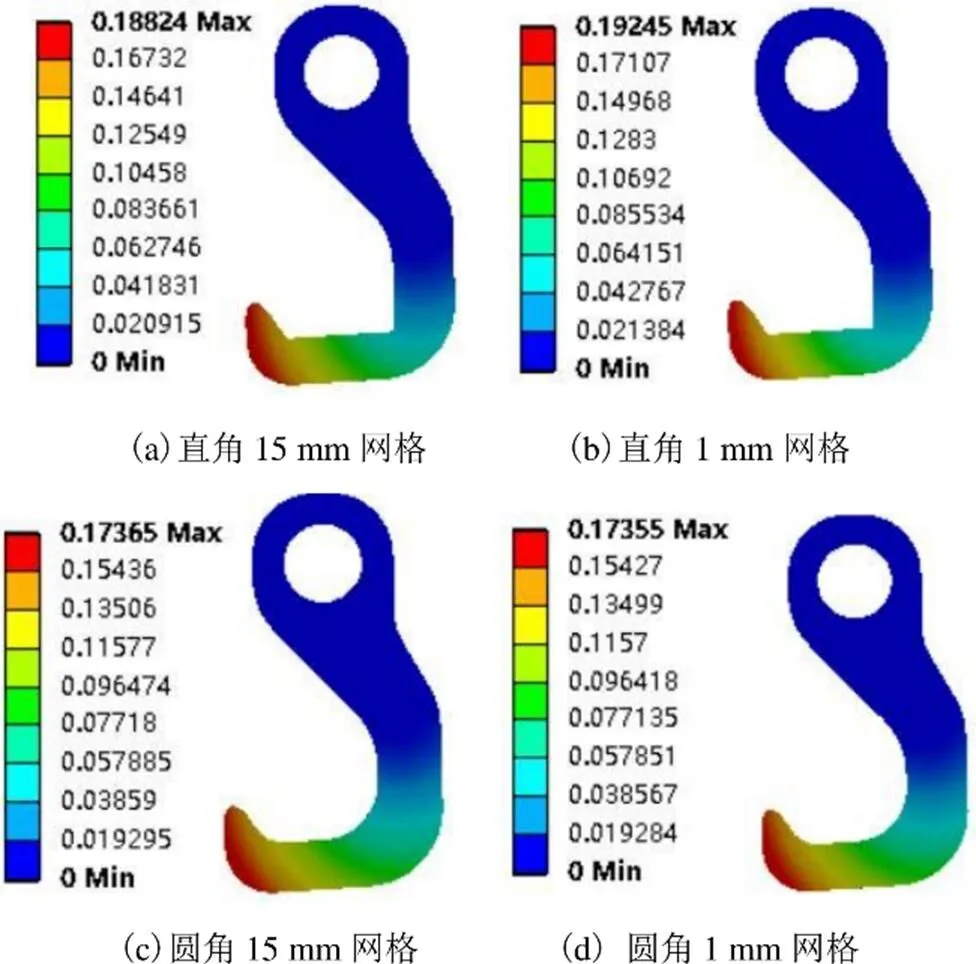
图13 吊钩位移解

3 应力集中与应力奇异区别

应力奇异现象只会存在于数值计算中，这是有限元求解应力问题时固有的缺陷与不足，也是应力集中与应力奇异现象在来源上的最本质区别。应力集中与应力奇异现象具有一定联系，但在一定情况下应力集中并不完全等同于应力奇异。这一现象可借由板孔实验进行研究。

采用结构为一端固定，另一端施加拉力的钢板进行研究，当网格尺寸为6 mm时，所求的的应力如图14所示；当网格尺寸为0.6 mm时，所求的的应力如图15所示。

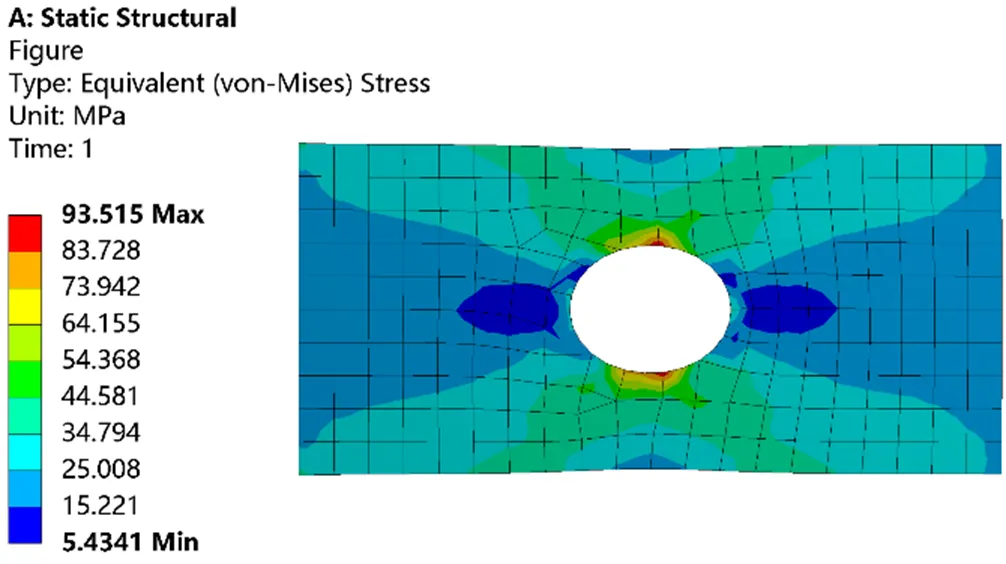
图14 网格尺寸为6 mm时的应力解

由求得的等效应力云图可知，在圆孔竖直方向的边缘位置应力值较大，存在应力集中现象，对模型进行网格细化，经二次求解后由计算结果云图可以看出，最大应力出现位置并未发生变化，表示最大等效应力数值的区域所覆盖的网格层数增加且求得的应力解也并未出现急剧上升，随着网格的加密，应力值越来越趋于稳定并且接近真实值，经计算前后两次求解应力误差为0.028%。因此，由上面的分析结果可以看出，板孔结构存在应力集中现象，但圆孔处的应力值并不随着模型网格的细化而发散，即所求得的应力解不存在应力奇异。例如圆孔附近的应力解是收敛解，所以应力集中出现位置不一定是应力奇异，但应力奇异现象出现的位置一定存在应力集中，这是二者的另一重要区别。

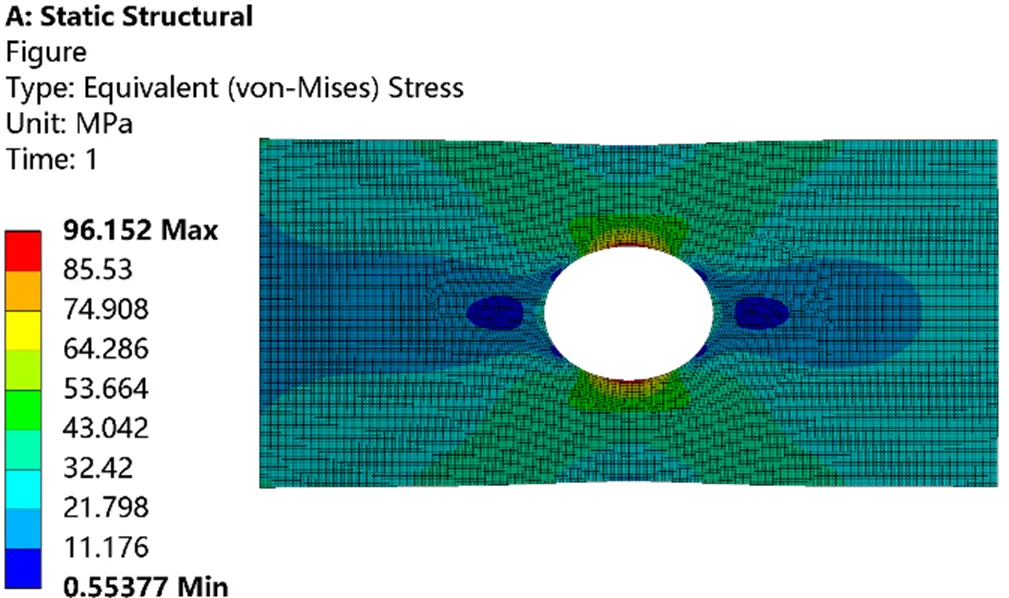
图15 网格尺寸为0.6 mm时的应力解

4 应力集中与应力奇异处理方法

4.1 保证计算过程中前处理符合求解要求

在有限元计算结构的应力时，其计算结果与网格的密度及划分质量有较大联系。在求解时首要的就是在保证材料本构模型正确的基础上，确保有限元分析的前处理过程中网格划分的数量及质量满足基本的求解要求。

一般的，在网格划分过程中，应保证模型的网格划分层数沿模型厚度方向最少划分出3层单元。此外，通过改善网格的相关中心、平滑度以及临近单元过渡等设置，可以使网格划分质量得到有效改善。对于具有复杂结构或大曲率型面的分析模型，使用带有中间节点的高阶单元同样有助于提升网格划分质量，同时由前面的分析可知，采用高阶单元也有助于提高求解精度。当网格划分完成以后，对网格划分质量进行评估时，对于静力学求解而言，一般选择平均网格质量及平均扭曲度两个准则作为网格划分后质量的评估。根据工程经验当平均网格质量数值Average>0.75，扭曲度Average<0.5时，即认为网格划分质量达到了求解标准。

4.2 应力集中现象的处理

4.2.1 通过结构改进来弱化应力集中现象

由前面的分析可知，应力集中主要是与零部件结构及材料性质有关，通过合理改进零件或装配体的结构可以有效改善应力集中现象。例如：可以在模型设计过程中增大结构中的圆角、增加圆弧槽或是通过改变具体结构来实现模型中力的传递路径的改变，将应力集中区域的应力有效分散；若零部件结构过于复杂，含有多处应力集中位置，在设计过程中，应尽量采用合理的结构来疏远应力集中过于密集的区域，目的是为了避免应力集中区域彼此间因为距离过近而出现应力叠加的现象，而防止应力陡升现象的出现；此外，对于结构中出现的局部应力较高的现象，在零件设计过程中对于局部位置增加加强筋及肋板，对于改善局部位置的应力集中现象以及提升整体刚度均有一定帮助。

4.2.2 不同材料对应力集中的处理方法

通常零件在静载荷作用下，不同材料对于应力集中问题的考虑是不同的。对于塑性材料来说，由于材料本身的静力学特点，材料在承受外部载荷以后，由于划痕、局部的几何缺陷或是细微圆角等局部细小的几何结构所引起的应力集中问题，在实际应用中，会因为所在位置的局部细微的塑性形变而得到缓解。此时，在静力学校核过程中就可以忽略应力集中对零部件性能的影响。

当零部件内部组织均匀，但为脆性材料时，此时就应考虑应力集中现象对零部件性能的影响，主要原因在于脆性材料不会像塑性材料通过局部的塑性形变来降低局部应力，一旦在脆性材料中出现了应力集中现象，在局部高应力区内极易产生裂纹等缺陷，在外力作用下会迅速降低产品的可靠性，缩短其使用寿命；当零部件是由铸铁等内部组织非均匀的脆性材料铸造而成时，受冶金作用的影响其结构内部的晶粒通常较为粗大，且具有较大的不均匀性，同时还有铸造产生的相应缺陷。这两者均是引起构件出现应力集中现象的重要因素。但铸件为了便于脱模，其结构上均含有铸造圆角，对于铸件来说因结构外形骤变引起的应力集中现象反而不明显。因此，静载荷作用时铸件可不考虑应力集中现象的影响；若构件承受动载荷，无论组成材料是塑性材料还是脆性材料，均应考虑应力集中现象对结构的影响。相对应的，应力集中对构件的疲劳寿命具有重要影响，通过以上分析可以得出，无论构件由上述哪一种材料构成，在对结构进行疲劳可靠性分析时，都必须考虑到应力集中现象对于疲劳寿命的影响。

4.2.3 复杂模型出现应力集中的处理方法

在对于产品结构进行静力学结构校核时，通常单个零件或是装配体结构复杂的情况下，单单凭借经验是很难准确估计出结构中的应力集中位置，这时有限元技术就可较好地解决这一问题。校核产品的刚度与强度过程中可以首先对有限元的分析模型进行较为粗糙的网格划分，即试算，在网格划分质量满足基本的静力学要求时，这样可以较为迅速的锁定应力集中位置，同时对于远离应力集中区域部分的结果是具有较高可靠度的。而对于结果中应力集中区域，可以采用局部网格加密二次计算的方法求得应力集中位置较为准确的应力解。常采用的二次计算方法主要有利用“影响球”功能进行局部加密或是子模型技术进行局部位置的网格精细化划分，用以得到较为准确的收敛解。

4.3 应力奇异现象的处理

应力集中与应力奇异现象相伴且共生，通过前面的分析可知，存在奇异解的有限元模型，在奇异解位置一定会有应力集中现象。想要消除奇异解，其本质还是应该首先解决模型中的应力集中问题。由于求解过程中模型的过度简化，所引入的任何一处尖角位置，都可能会导致计算过程中出现奇异解。因此，计算过程中能够合理简化圆角结构就显得尤为重要。此外，在计算过程中根据零件或装配体实际工况，合理添加约束和载荷也是避免奇异解出现的重要因素。通常静力学分析中，在固定约束位置易出现应力奇异解，因此需要工程人员合理分析实际工况适当使用固定约束。

在对于奇异解的处理问题上，对于非关键位置可以采用局部比例尺涂白进行处理；当分析模型的过度简化，致使模型中存在锐利的尖角或直角边且分析模型过于庞大时，可采用子模型分析技术，进行模型的二次创建，求出较为精确的收敛解；总而言之，对于应力奇异问题的处理办法，最为行之有效的措施就是在模型出现奇异的直边位置添加圆角或圆弧过渡面。

4.4 网格无关解校验

在有限元计算过程中，当单元内部不满足平衡方程，或是单元与单元交界面上的应力存在不连续性，又或者在力的界面上不满足外载施加的边界条件，以上3种情况在有限元求解过程中都会带来离散误差。在有限元求解过程中当模型本构、单元类型、边界条件与外载的施加均不变的情况下，有限元技术所求的应力解与网格的尺寸是具有极其密切的联系的。

4.4.1 有限元求解产生误差的原因

有限元计算结果存在一定的误差，误差的本质是有限单元分析的计算结果与数学模型精确解间的不一致性。有限元计算过程将连续体离散成带有公共节点的单元形式进行逼近，这就意味着只要采用有限元技术进行求解就会带来离散化误差。当有限元模型中的单元趋近于无穷小则可近似的认为，模型等同于原来的连续体而消除离散化误差，然而在实际计算中这一过程是不可能实现的。有限单元解法会受到网格数量、每个网格上的节点数量、单元形状函数的性质、等参数单元所用的积分规则以及特殊单元其它公式化细节的影响。而离散误差的大小取决于模型离散方程的截断误差（舍入误差）的有效数字位数。通常截断误差在应用求解算法之前就已经存在于所采用的单元和结构矩阵之中。正常在相同的网格步长之下，截断误差的阶数越高（有效数字位数越多），相对应的离散误差就会越小。对于相同的离散方式，单元数量越多，对应的离散误差也会越小。模型划分出足够细化的网格，就可以确定出“真实的”收敛率。网格的细化需要有度，在计算过程中显然不可能采用单元尺寸趋近于0的单元步长，因为这会带来离散方程数目的激增，致使计算量过大，由于方程求解次数的激增，会导致数值解埋没于舍入误差之中。

4.4.2 消除有限元求解误差的方法

在实际应用中，网格细化的程度应该是在工程允许的误差范围内，模型经网格细化操作后所求得的结果，与前一次相比几乎不再发生变化，这样所获得的解就是网格无关解。这一方法有助于缩小离散误差得到较为精确地结果，同时也有助于校验所求解中是否存在奇异解。

相对应的，对于一个科学且严谨的有限元分析，就必须校验所求得的静力学结果与网格的疏密程度是无关的。目前，获得网格无关的解是国际学术界接受数值模拟类论文的基本要求，并且在粗分网格与精细化划分的网格条件下，前后两次求解误差应保持在3%的误差范围以内，或者需要更小误差来满足工程需求。由前面对于直角与圆角模型的分析可以看出，不同类型的求解单元对求解精度存在一定影响，因此还可以校验计算结果在不同网格类型下的无关性。

5 结论

应力集中与应力奇异现象是静力学求解中常见的工程问题，奇异解的出现对产品强度及疲劳寿命的校核均会产生较大影响，通过上述系列研究得到如下结论：

(1)应力集中与应力奇异在来源上有本质区别，应力集中现象存在现实的结构当中，而应力奇异现象仅存在于数值计算之中；存在应力集中的位置不一定存在奇异解，但是存在奇异解的位置一定存在应力集中。并且在有限元计算过程中，对于应力奇异解，网格划分的越细，应力结果越大，趋于发散。

(2)高阶单元相比于低阶单元，计算结果具有更高的可信度，四面体低阶单元计算结果可信度最低，在模型网格划分较为粗糙时，具有较大的误差。

(3)位移解受模型网格划分疏密程度影响较小，即使是采用较为粗糙的网格进行计算，也可较为准确的估计出模型的位移解。

(4)改善模型中应力集中的较好方法是增加大弧度圆角结构，对于解决应力奇异的最行之有效的方法也是合理的添加圆角结构。

(5)在有限元计算过程中，当出现奇异解时，除合理修改结构和划分网格外，对于本构模型、边界条件及外载、初始条件的检查也非常必要。

(6)在有限元分析中，子模型技术对于获得复杂结构较为精确的应力解具有突出优势，并且对于合格的数值模拟分析，应进行网格无关解校验。

[1] 徐丽, 高嵩, Nigel Barltrop. 存在奇异点的结构疲劳评估简单方法[J]. 船舶工程, 2013, 35(6): 9-14.

[2] Abdelhak Khechai, Abdelouahab Tati, Abdelhamid Guettala. Finite element analysis of stress concentrations and failure criteria in composite plates with circular holes[J]. Frontiers of Mechanical Engineering, 2014, 9(3): 281-294.

[3] Alireza Fallahi Arezoodar, Ali Baladi. The Effects of Materials Properties & Angle Junction on Stress Concentration at Interface of Dissimilar Materials[J]. Advanced Materials Research, 2012(1518): 887-892.

[4] Murer S, Leguillon D Static and fatigue failure of quasi-brittle materials at a V-notch using a Dugdale model[J]. European Journal of Mechanics - A/Solids, 2009, 29(2): 109-118.

[5] 张进, 吴健, 王纬波, 等. 45钢椭圆孔板应力集中的应变率效应[J]. 机械强度, 2020, 42(3): 694-699.

[6] 唐洪祥, 管毓辉. 孔口应力集中问题的Cosserat连续体有限元分析[J]. 东南大学学报：自然科学版, 2013, 43(4): 849-855.

[7] 张永锐. 三维切口板应力奇异性分析[D]. 合肥: 合肥工业大学, 2017.

[8] 谭林. 薄板孔边应力集中的尺度效应研究[D]. 重庆: 重庆大学, 2015.

[9] 周炬, 苏金英. ANSYS Workbench 有限元分析实例详解 (静力学) [M]. 北京:人民邮电出版社, 2017.

Finite Element Study of Stress Concentration and Stress Singular Phenomenon for Engineering Applications

GAO Si-yuan1, ZHAO Xu-dong2, LI Wei-min2, JIANG Guo-hai2

（1. Department of Mechanical and Electronic Engineering, Jinzhou Normal College, Jinzhou 121001, China;2. College of Mechanical Engineering and Automation, Liaoning University of Technology，Jinzhou 121001, China）

The causes of stress concentration and stress singularity are analyzed and summarized. The changes of stress concentration and stress singularity in the process of finite element solution are studied. In addition, the influence of different mesh types and sizes on the finite element solution accuracy is analyzed.. Then the difference between stress singularity and stress concentration is discussed. Finally, the engineering solutions to the problems are summarized.

finite element technology; stress concentration; stress singularity; grid-independent solution test

10.15916/j.issn1674-3261.2021.05.001

TH164

A

1674-3261(2021)05-0281-07

2020-10-27

辽宁省教育厅科学技术研究项目(CYYJY-201802)

高思远(1982-)，男，辽宁锦州人，讲师，硕士。

责任编辑：陈 明