叶轮搅拌非牛顿流体时的功耗特性研究

王 鹏，段江龙，王世基

(1.江苏大学流体机械工程技术研究中心，镇江 212013；2.山东双轮股份有限公司，山东 威海 264200)

随着全球能源和环境问题日益凸显，努力寻求解决全球能源需求与环境保护之间的平衡问题已迫在眉睫.生物质能源(如沼气等)是一种能从处理工农业废弃物中回收利用的可再生清洁能源，在全球范围内已备受重视.生物质能源作为我国能源结构的重要组成部分，至2020年，其每年转化为能源的潜力为4.6亿吨标准煤，占一次能耗总量的10%，其研究和开发对提高我国新能源利用和占有率具有举足轻重的作用[1-2].研究表明，在对工农业废弃物回收利用以获得新能源的过程中，机械搅拌过程对生物质能源的充分回收利用具有重要的影响[3].作为整个厌氧消化过程中至关重要的一个步骤，搅拌叶轮使发酵原料与微生物充分混合、均匀接触，从而使得微生物的食料充足，保证充分发酵，提高产气率，防止物料结壳和沉淀[4].因此，搅拌叶轮的搅拌功耗高低直接关系到可再生能源的回收利用率，而如何预测搅拌系统的功耗损失以及提高搅拌效率是一个亟待解决的问题.

由于发酵工程中的发酵液呈剪切稀化非牛顿流体特性，其粘度随着剪切速率呈非线性变化，致使机械搅拌过程的功耗特性及雷诺数的计算更加复杂.为了精确的预测其功耗特性及相应的雷诺数，有学者提出了功率准数(Ne)与广义雷诺数(ReN)的方法来表征整个搅拌系统的功耗特性，如图1所示.在搅拌系统中，功率准数与广义雷诺数的关系可定义为当ReN<10时为层流区、当1010 000时为湍流区[5].在层流区，其主要的特征是功率准数与广义雷诺数的乘积为一常数，且该段直线的斜率为-1.在转捩区，其功率准数曲线持续下降，在靠近湍流区的地方趋于平缓.而在湍流区，功率准数基本不随广义雷诺数的增加而改变，即为一定值.

研究发现，在利用已有的功率准数与广义雷诺数公式来预测一个搅拌系统的功耗特性时，对于不同的广义雷诺数定义式有着不同的差异[6-10].因此亟需争对任意搅拌系统推导适用性更广的功率准数与广义雷诺数公式，使其能够更加精准的预测诸如沼液搅拌等场合.

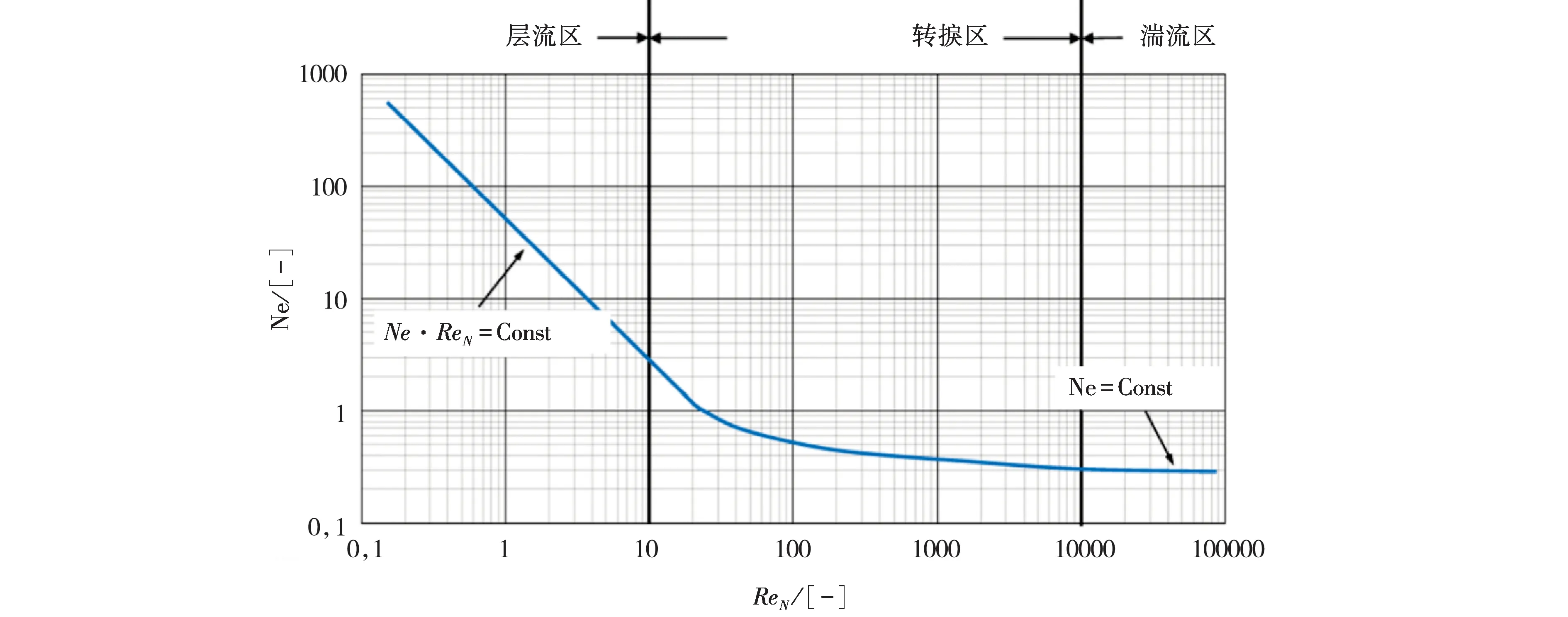
图1 搅拌系统中功率准数与广义雷诺数的分区定义

图2 搅拌系统试验装置图

图3 (a)搅拌系统不同尺寸叶轮及搅拌罐示意图 (b)搅拌叶轮三维图

2 实验材料与方法

2.1 试验装置

本实验过程采用自主设计的实验平台，如图2所示.其中，1为驱动电机，可实现正反转；2为扭矩仪，可测量搅拌叶轮的转速及扭矩(测量范围为0.5 N·m)，其测量误差为2 rpm和0.001 N·m；3与4为反应器盖板；5为空气轴承，可减小轴的摩擦导致的误差；6为轴，轴端可固定搅拌叶轮.

2.1.1 反应器与搅拌叶轮几何参数

本研究采用两种尺寸的反应器与叶轮来完成实验，其中反应器及搅拌叶轮的相关几何尺寸如图3所示，其具体的几何尺寸如表1和表2所示.

表1 不同尺寸及外径的搅拌罐及叶轮

表2 大小搅拌系统的几何尺寸

2.2 试验流体

由于沼液具有非牛顿流体特性，其发酵过程中的不同发酵程度的沼液的流变特性极其复杂.因此，为了模拟沼液发酵过程中不同浓度沼液对搅拌叶轮功率的影响特性，本研究中采用与沼液具有相似流变特性的不同浓度的羧甲基纤维素钠 (CMC)溶液作为试验流体.因此，本试验采用4种不同浓度的CMC溶液作为试验流体，其中编号0为牛顿流体(水)，其相关物理特性如表3所示.

表3 不同浓度溶液的流变特性

为了测量CMC溶液的流变特性，本实验采用BROOKFIELD R/S流变仪来测量CMC溶液的流变特性.经过测试及数据拟合得知，CMC溶液满足Ostwald-de Waele[11]的幂律型非牛顿流体函数方程，其本构方程为

(1)

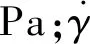
进一步，上式可简化为动力粘度η与剪切速率的关系.

(2)

试验所涉及的非牛顿流体的流变特性如图4所示.

图4 试验所用的CMC溶液的剪切应力与剪切速率的关系

因此，搅拌器中雷诺数可定义为

(3)

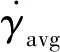
(4)

公式中：ks为Metzner常数.但是该假设是基于整个搅拌过程为层流状态所提出的，大量研究也证明了其在层流状态下的适用性，并得出了ks=11.5这一结论.由此，搅拌器中层流流动的广义雷诺数可定义为

(5)

此外，Metzner和Reed[12]基于管道流动提出利用有效动力粘度来计算管道内广义雷诺数的方法.该方法中，利用有效粘度ηeff来替代牛顿流体雷诺数定义中的粘度为

(6)

(7)

结合公式(1)和公式(2)可得出有效粘度的表达式为：

(8)

因此，基于Metzner 和 Reed假设的广义雷诺数的表达式为

(9)

此外，Chhabra等[13]通过假设非牛顿流体在圆管内流动，以此推导出了一个适用于圆管内非牛顿流体层流流动的广义雷诺数为

(10)

2.3 功率测量和功率准数

实验使用扭矩传感器测定搅拌功率，通过安装在轴上的扭矩传感器测得搅拌过程中叶轮的扭矩(M)与转速(N)，则搅拌功率P由下式计算.

P=2πNM.

(11)

由于在测量过程中联轴器晃动及搅拌过程带来的不稳定性，在搅拌叶轮轴上安装空气轴承以减小摩擦造成的误差，试验时待搅拌系统运行稳定后，在10分钟内每5 s测量一组，最后取多次测量扭矩及转速值的平均值.

功率准数Ne是无量纲数，是用于表征搅拌功率输入性能的参数，同时也是表征搅拌叶轮自身性能的一个特征参数，其定义为

Ne=P/ρN3D3，

(12)

公式中：ρ为液体密度；D为叶轮外径.

3 试验结果与分析

根据试验要求，完成不同浓度的CMC溶液的搅拌及数据的采集.首先基于已有的三个广义雷诺数对试验过程的功率准数数据进行分析.功率准数Ne随Metzner和Otto广义雷诺数ReMO的变化曲线如图5所示.由图5可知，试验测量的牛顿流体的功率准数在层流及转捩区明显高于不同尺寸及浓度的功率准数，但不同流体的功率准数与广义雷诺数具有相同的变化趋势.层流状态下的功率准数最大，随着广义雷诺数的增加，在转捩后区功率准数的变化趋势趋于平缓；当雷诺数大于100后，非牛顿流体的功率准数与牛顿流体的功率准数基本吻合.此外，对比不同大小的搅拌叶轮及搅拌槽的功率准数可知，在层流区浓度0.62的CMC溶液具有较高的功率准数，但是在转捩区其功率准数却偏小趋势.在雷诺数大于100的区域，CMC溶液浓度0.15的大搅拌叶轮的功率准数最接近牛顿流体的功率准数，但是各个尺寸搅拌叶轮及浓度的搅拌槽的功率准数除了具有相同变化趋势外，没有其他变化规律.

图5 不同尺寸及溶液的功率准数与广义雷诺数ReMO的变化曲线

功率准数与Metzner和Reed广义雷诺数ReMR的变化曲线如图6所示.由图6可知，相比广义雷诺数ReMR，牛顿流体的功率准数与非牛顿流体的功率准数在层流区基本吻合，且率低于部分非牛顿流体搅拌的功率准数.牛顿流体的功率数只有在广义雷诺数大于800左右时，其功率准数明显低于所有非牛顿流体搅拌的功率准数.对不同尺寸及浓度的非牛顿流体搅拌，可知在层流区时，不论叶轮大小尺寸，高浓度的非牛顿流体则具有高的功率准数.此外，在转捩区及靠近湍流区的地方，非牛顿流体的功率准数变化随着广义雷诺数的增加其趋势趋于平缓.

图6 不同尺寸及溶液的功率准数与广义雷诺数ReMR的变化曲线

功率准数与Chhabra广义雷诺数ReCH的变化曲线如图7所示.由图7可知，在该广义雷诺数定义下，牛顿流体的功率准数在层流区明显低于大部分非牛顿流体搅拌的场合；但在转捩区却明显高于各非牛顿流体搅拌系统，在广义雷诺数大于450的区域远低于各非牛顿流体搅拌场合.对不同尺寸的非牛顿流体的搅拌，再次，在层流区，对高浓度的CMC溶液仍然具有高的功率准数.可以观察到，在雷诺数大于100的区域，所有非牛顿流体的功率准数基本重合，且其变化趋势趋于平缓.特别地，在转捩区浓度0.45的CMC溶液大尺寸的搅拌系统的功率准数最小，在雷诺数大于100后，功率准数再次与其他的搅拌系统功率准数重合.

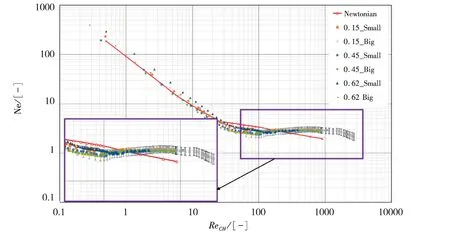
图7 不同尺寸及溶液的功率准数与广义雷诺数ReCH的变化曲线

由上述分析可知，对已有的研究搅拌器内功率准数与广义雷诺数的关系式只适用于层流区，而在转捩区则出现了很大的偏差.因此，亟需对不同的搅拌系统在搅拌非牛顿流体时，搅拌器内从层流到转捩的整个流动过程的功率准数与广义雷诺数之间的关系进行深入研究，提出一个新的关系式以适用不同尺寸的搅拌系统.基于此，本研究从非牛顿流体的流变特性及已有的试验数据出发研究推导一个新的功率准数与广义雷诺数公式.

首先，基于非牛顿流体的流变特性，可知

(13)

(14)

(15)

根据公式(10)可知输入功率与扭矩关系，可由此假设扭矩(M)的产生主要来自有效力(Ff)与搅拌叶轮的直径(d)有关，即

M∝Ff·d.

(16)

而有效力又与剪切应力相关联，即：

Ff∝τf·d2.

(17)

有相似理论可知，搅拌容器的体积可表达为：

V∝d3.

(18)

由公式(11)、公式(16)及公式(18)可得到公式(17)中的有效剪切应力τf的表达式为

(19)

由Bao等[14-15]可知，定义Cp为比例因子，P/V为特定的功率输入.同时可得出有效剪切应力为

(20)

结合公式(11)可得有效剪切速率为

(21)

公式中：

(22)

为剪切指数，其与比例因子有关.因此，功率输入可通过公式

(23)

计算.进而可得出

(24)

对于平底搅拌槽的体积可定义为

(25)

由于功率输入特性仅在一个恒定的几何关系下有效，因此，搅拌槽的体积可转化为

(26)

(27)

因此，搅拌槽的容积可表示为

V=Cg·d3，

(28)

公式中：

(29)

是与搅拌槽相关的几何因子.由于对于不同的假设，剪切系数的推导于剪切速率有关，因此，基于[16]所提出的假设，剪切速率的表达式为

(30)

(31)

q=1-k1.

(32)

在层流区(当k1=1时)，剪切速率可定义为

(33)

公式中：klam为层流区系数，结合公式(7)可得

(34)

由此可得到剪切系数为

(35)

结合上述各式可得

(36)

结合公式(6)、公式(11)及公式(34)可得出一个新的广义雷诺数的表达式为

(37)

在层流区，功率准数可表示为

Ne=klam·Re-k1.

(38)

其中对大多数搅拌系统而言k1=1，层流区系数klam，且满足层流区的流动规律为

klam=Ne·Re.

(39)

其中klam与搅拌系统中搅拌叶轮的位置及相关几何参数有关.根据参考文献[12]可知，klam可表示为

(40)

结合公式(35)和公式(36)可得出一个新的适用于本搅拌系统的广义雷诺数为

(41)

其中

(42)

对新推导的广义雷诺数公式进行试验验证，其功率准数与新广义雷诺数结果如图8所示，由图8可知，新公式不仅能很好的预测该搅拌系统在层流区的功耗特性，同时在层流和转捩区也能很好的预测其功耗特性，进而进一步证实了新公式的广泛的适用性.

图8 不同尺寸及溶液的功率准数与新广义雷诺数Renew的变化曲线

4 结 论

(1)基于Metzner &Otto的广义雷诺数ReMO可知，牛顿流体的功率准数在层流及转捩区明显高于非牛顿流体搅拌过程，当ReMO>100后，非牛顿流体的功率准数与牛顿流体的功率准数基本吻合;

(2)基于Metzner &Reed的广义雷诺数ReMR可知，在层流区，搅拌牛顿流体的功率准数搅拌非牛顿流体时基本吻合；但在ReMR>100时，明显低于非牛顿流体的功率准数，且在转捩区非牛顿流体的功率准数基本不随雷诺数的增加而改变;

(3)基于Chhabra的广义雷诺数ReCH可知，在层流区牛顿流体的功率准数明显低于非牛顿流体的功率准数，特别是在ReCH>450后；在转捩区浓度0.45的CMC溶液大尺寸的搅拌系统的功率准数最小，在ReCH>100后，功率准数再次与其他的搅拌系统功率准数重合;

(4)对本研究的试验数据基于新推导的广义雷诺数公式进行整个搅拌系统的功率准数的预测，新公式显示了在层流及转捩区都能很好的与牛顿流体的功率准数高度吻合，证明了新的广义雷诺数的广泛适用性.