粒子群算法在带导叶离心泵性能优化中的应用

王文杰，邓起凡，裴 吉，王家斌

(1.江苏大学 国家水泵及系统工程技术研究中心，江苏 镇江 212013；2.山东双轮股份有限公司，山东 威海 520000)

借助于数值仿真和可视化试验手段，泵内部流动规律得到深入研究，泵设计理论也得到发展，传统的一元设计方法只能依赖半理论半经验公式，往往要借助于经验公式，系数多，需要反复尝试，才有可能使泵性能达到最优.而先进的三元设计方法则利用数值模拟软件获得泵内流特性和性能参数，基于CFD的性能预测泵初始化设计之后的重要研究内容.国内外专家学者对泵性能优化方法开展了长期的研究.常用的优化方法如下：(1)通过固定泵其他几何参数，改变单一几何参数，得到其对性能的影响规律[1-4]，这是一种简单快捷的优化设计方法；(2)结合内部流动规律以及统计大量优秀泵水力模型，简化推导泵性能优化目标的半经验半理论计算公式，完善泵设计方法[5-6].其中，应用较为广泛的一种方法为水力损失法；(3)采用正交试验设计方法，基于设计变量的个数及水平选取合适的正交表，采用极差分析法研究多个设计参数对优化目标的影响程度，再通过组合，获得较优目标的最优组合方案[7-9]；(4)采用试验设计与近似模型建立优化目标值和设计变量之间高精度的近似数学函数表达式[10-14]；(5)采用伴随方法优化性能，采用伴随方程求解控制方程(流场)，从而减少数值计算资源[15-16]；(6)智能优化算法直接优化性能[17-19]，主要采用的是经典的遗传算法.

然而，在泵优化过程中，泵性能和几何变量之间是强非线性的数学关系，建立优化目标(效率、扬程、空化等)与设计变量之间的近似数学模型精度低，不能精确获得最优值.伴随方法虽然不考虑设计变量个数，但是其本质上属于梯度类优化方法，无法实现全局寻优.因此，本文以带导叶离心泵为优化对象，提出一种基于改进的实时自适应粒子群算法的叶轮多参数自动优化方法，采用改进的粒子群优化算法自动对叶轮的10个设计变量在全局范围内进行寻优，以获得满足扬程设计要求下效率最高的参数组合.

1 计算模型与数值模拟

1.1 模型泵

带导叶离心泵的水力部件由叶轮、导叶和环形蜗壳组成，如图1所示.其性能设计参数为：流量Q=910 m3/h，扬程H=77 m，转速n=1 490 r/min.泵的主要几何参数如表1所示.

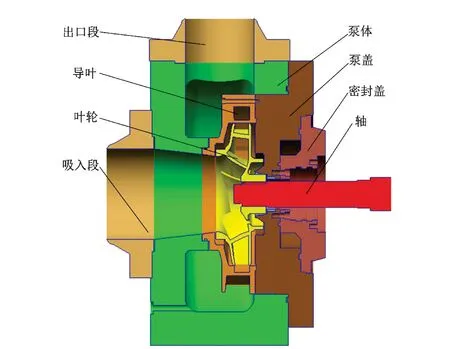
图1 带导叶离心泵三维图

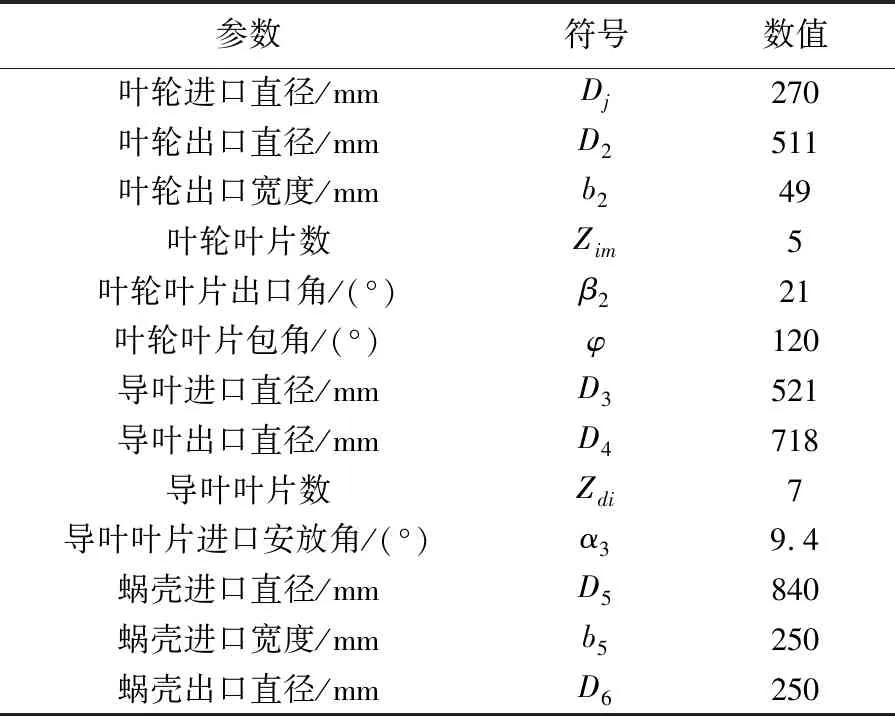
表1 带导叶离心泵几何参数

1.2 数值模拟

采用Turbo Grid软件对叶轮计算域进行六面体网格划分，如图2所示.根据前期的网格无关性分析[20]，网格总数取350万时，计算的扬程保持不变.此对，对比全流场和非全流场的外特性数据，发现两种条件下设计工况下的性能参数差异较小[21].整个计算域包括进口段、叶轮、导叶和蜗壳4个水力部件，未考虑口环间隙和前后腔如图3所示.在定常计算设置中，选取SST湍流模型封闭N-S方程进行求解.进出口边界条件分别设为总压和质量流量.进口总压为一个标准大气压，出口设置为设计工况的质量流量.旋转域和静止域的交界面设置为“Frozen Rotor”，而静止域之间设置为“None”，计算域之间网格采用GGI连接方式.计算精度为高阶精度，计算残差设置为10-5，迭代数为500.

2 带导叶离心泵叶轮性能优化

2.1 粒子群算法

1995年美国学者James Kennedy和Russell Eherhart提出了粒子群优化算法[22-23]，是一种群智能算法.其基本思想是模仿自然界鸟群、鱼群搜索食物的行为方式.

图 4 粒子运动示意图

在算法迭代过程中粒子位置更新示意图如图4所示，粒子具有速度v和位置s两个属性.粒子群算法迭代计算的基本数学方程为公式(1)和公式(2).

vi，t+1=vi，t+c1×rand1i×(pbesti-xi，t)+

c2×rand2i×(gbesti-xi，t)，

(1)

xi，t+1=xi，t+vi，t+1，

(2)

公式中：xi，t和vi，t分别为在迭代时刻t第i个粒子的位置和速度；c1和c2分别为自身认识学习速度和社会学习速度的学习因子，rand1i和rand2i为随机因子，在0和1之间随机取值.

考虑粒子与全局最优粒子间在每个维度下的距离，粒子之间的距离定义为[24]

dis=xg-x，

(3)

(4)

(5)

w=(wmax-wmin)×dis2/(dismax/2)2+wmin.

(6)

根据粒子群算法改进中加快全局搜索能力的经验(随算法的不断迭代，惯性权重减小，自我学习因子减小，社会学习因子变大).对公式(4)～公式(6)中的c1max、c2min和wmax分别进行了补充，建立了三个变量随迭代数线性变化的表达式，提高了实时自适应粒子群算法系数改进方法.

c1max=3.2-1.2/tmax×t，

(7)

c2min=0.5+1.5/tmax×t，

(8)

wmax=1.2-0.4/tmax×t.

(9)

2.2 优化目标

以带导叶离心泵在设计工况的效率为优化目标，通过数值模计算泵进出口压力和扭矩，得到泵效率.计算公式为

(10)

公式中：Qd为设计工况下的流量，m3/h；p1tot、p2tot分别为泵进出口总压，Pa；T为叶轮扭矩，N·m；ω为叶轮旋转角速度，rad/s.

在带导叶离心泵效率优化过程中，扬程的设计要求范围为[71 m，77 m]，人为地对缩小扬程设计范围，扬程的约束条件表达式为

(11)

在编写泵效率化智能程序中，优化目标函数定义为效率的相反数，可变成求解最小值问题.当粒子群优化算法中粒子(叶轮)在三维造型或者网格划分失败，无法得到数值模拟值，人为地停止该方案的进，并将效率值设置为100，即视为无效值.如果当粒子的约束条件扬程超出了给定的约束范围，则人为地将优化目标设置为数值模拟得到的效率(正值)，即为无效值.

3.3 优化变量

由于泵整体结构尺寸的限制，仅对叶片型线进行优化设计.叶片安放角、叶片进口边位置和叶片厚度分别由五阶、三阶和三阶Bézier曲线进行控制.由于Bézier曲线上控制点在水平方向的坐标值是有序的，设定Bézier曲线控制点固定在水平方向并均匀分布.控制点可以在竖直方向上自由移动，固定叶片进口边在前后盖板上的位置，同时叶片进口边和出口边的厚度固定.最终选取了10个设计参数(表2)，其中叶片进口边位置有2个控制变量(x1、x2)、叶片安放角有6个控制变量(x3～x6)，叶片厚度有2个控制变量(x9、x10).在叶轮三维造型BladeGen软件中，叶片型线如图5～图7所示.

表2 10个设计变量的范围

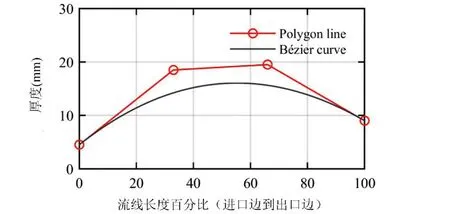
图7 叶片厚度变化的Bézier曲线

2.4 粒子群算法参数设置

根据文献[25-26]对种群数的研究，选取种群数为优化变量的2倍，即20个粒子数，采用拉丁立方试验设计方法对20个粒子进行空间分布初始化.在工程实际中，泵效率取4位有效数字，选取收敛残差为10-5，设定迭代数为50次.

3 结果与分析

3.1 外特性实验验证

图8 带导叶离心泵开式测试台

为了验证带导叶离心泵性能数值模拟的准确性，采用不锈钢材料加工制造叶轮和导叶.在江苏大学国家水泵及系统工程技术研究中心实验室的开式实验台上完成导叶离心泵外特性测量，如图8所示.开式实验台满足国家Ⅱ级测试精度.采用上海威尔泰仪器仪表有限公司生产的WT200智能压力变送器测量泵进出口静压，进口压力变送器的量程为-0.1～0.1 MPa，出口压力变送器的量程为0～1.6 MPa，测量精度均为 0.1级；采用开封仪表有限公司生产的MF/E2511621100ER11型电磁流量计测量泵流量，测量精度为0.5级.由于带导叶离心泵额定功率较大，为355 kW，采用降转速进行测试，测试转速为980 r/min.泵进口管路直径为350 mm，出口管路直径为250 mm.获得带导叶离心泵的外特性曲线后再通过泵相似换算定律得到其在额定转速下的外特性曲线.

对比离心泵外特性曲线如图9所示，从图9可以看出，两者的性能曲线变化趋势一致，在设计工况下，带导叶离心泵模拟扬程为75.2 m，效率为76.4%，实验扬程和效率分别为77.1 m和78.5%，扬程和效率的计算误差分别为2.5%和2.7%.因此，数值模拟得到的性能参数是可信的.

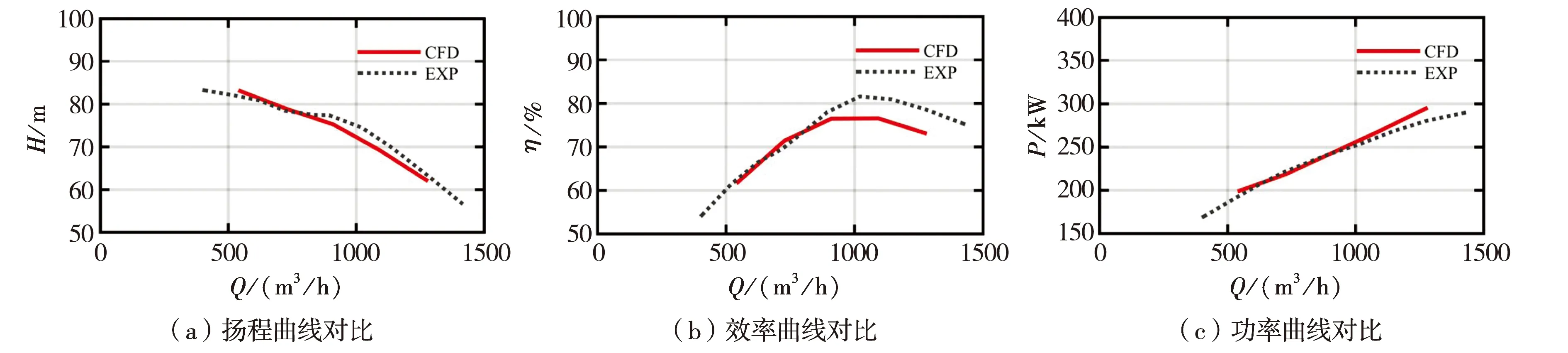
图9 数值模拟与试验外特性曲线对比

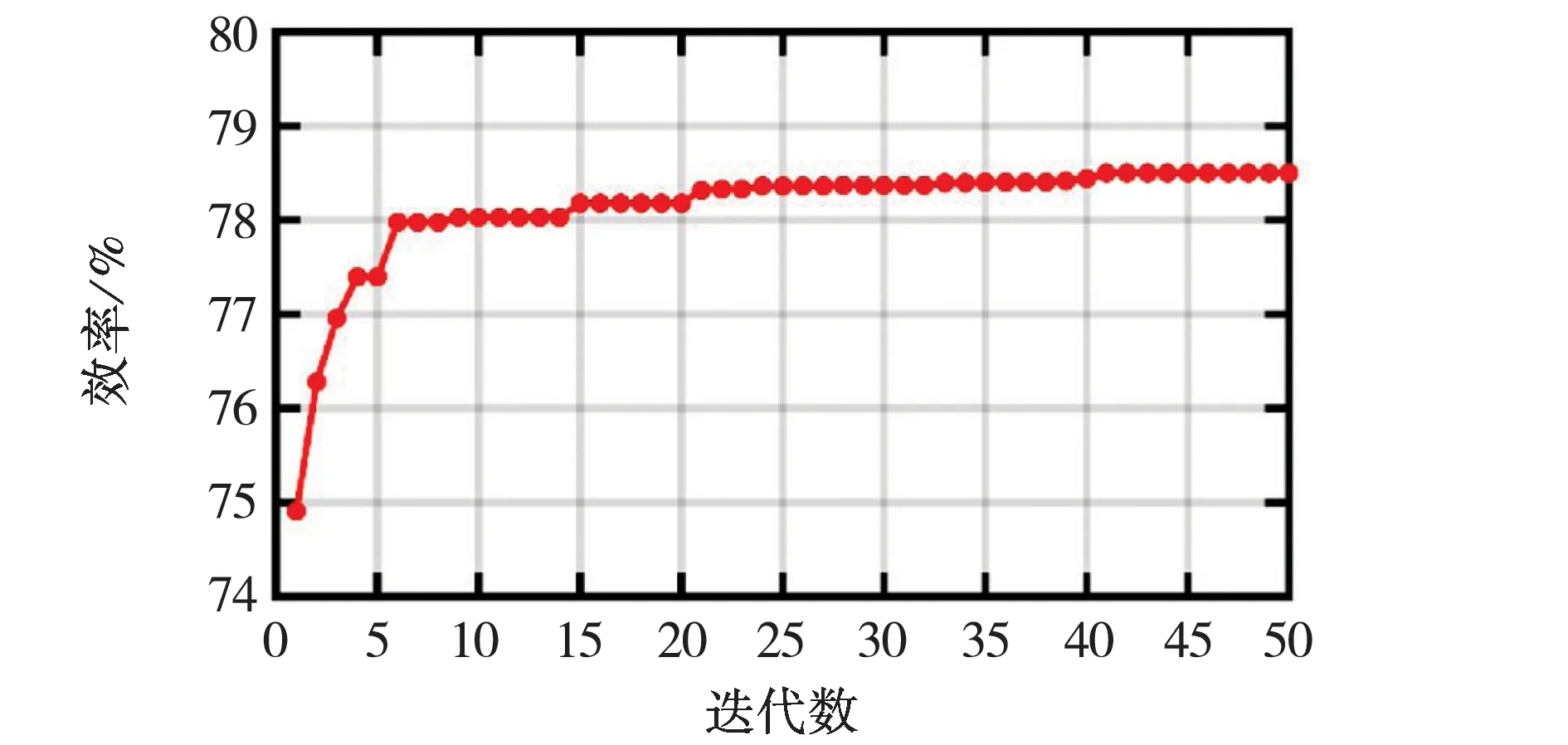
图10 泵效率在寻优过程中的变化趋势

3.2 带导叶离心泵叶轮优化过程分析

粒子群优化算法在迭代计算中不断对泵效率寻找最优值的过程曲线，如图10所示.在叶轮的自动优化计算过程中，采用的改进粒子群算法收敛速度快，自动优化计算经过50次迭代，收敛残差已达到10-5.在粒子群算法搜索的初期泵效率为74.91%，经过6次迭代后，泵效率达到77.97%，扬程为74.2 m，全局寻优速度快，在粒子群算法搜索后期泵效率增加到78.50%，扬程为72.5 m.经过优化后，泵效率可提高2.1%，扬程仍然满足设计要求.

5.3 带导叶离心泵叶轮优化内流场分析

为了揭示泵效率提高的机理，对比分析了原始叶轮和优化迭代过程中不同叶轮方案下泵内部速度流线图，如图11所示.在原始叶轮流道内在叶片工作面出现了回流，流动不符合在进口区域的叶片型线，产生较大的水力损失.在导叶内部速度分布不均匀，在一个流道内出现了较大的回流区，阻塞流道.在导叶叶片工作面产生了流动分离.在第一次迭代最优方案中，叶轮流道内速度分布并未得到改善，在叶轮的一个流道叶片工作面产生了较大的漩涡区域，产生水力损失，叶片背面的流动得到改善.导叶部分流道内流动分离产生的回流区域消失.在第4次迭代最优方案中，相对第一次迭代中的叶轮，叶片包角增加，叶轮叶片工作面上的不稳定流动得到改善，流动分离引起的回流区域减小或者消失，叶片背面流动符合叶片型线.导叶部分流道内流动得到改善，而部分流道回流区域增大.在第41次迭代最优方案中，叶片包角继续增加，在叶轮叶片工作面回流区域消失，但存在低速区，流动得到大幅度改善.

图11 不同叶轮方案的泵内部流线分布

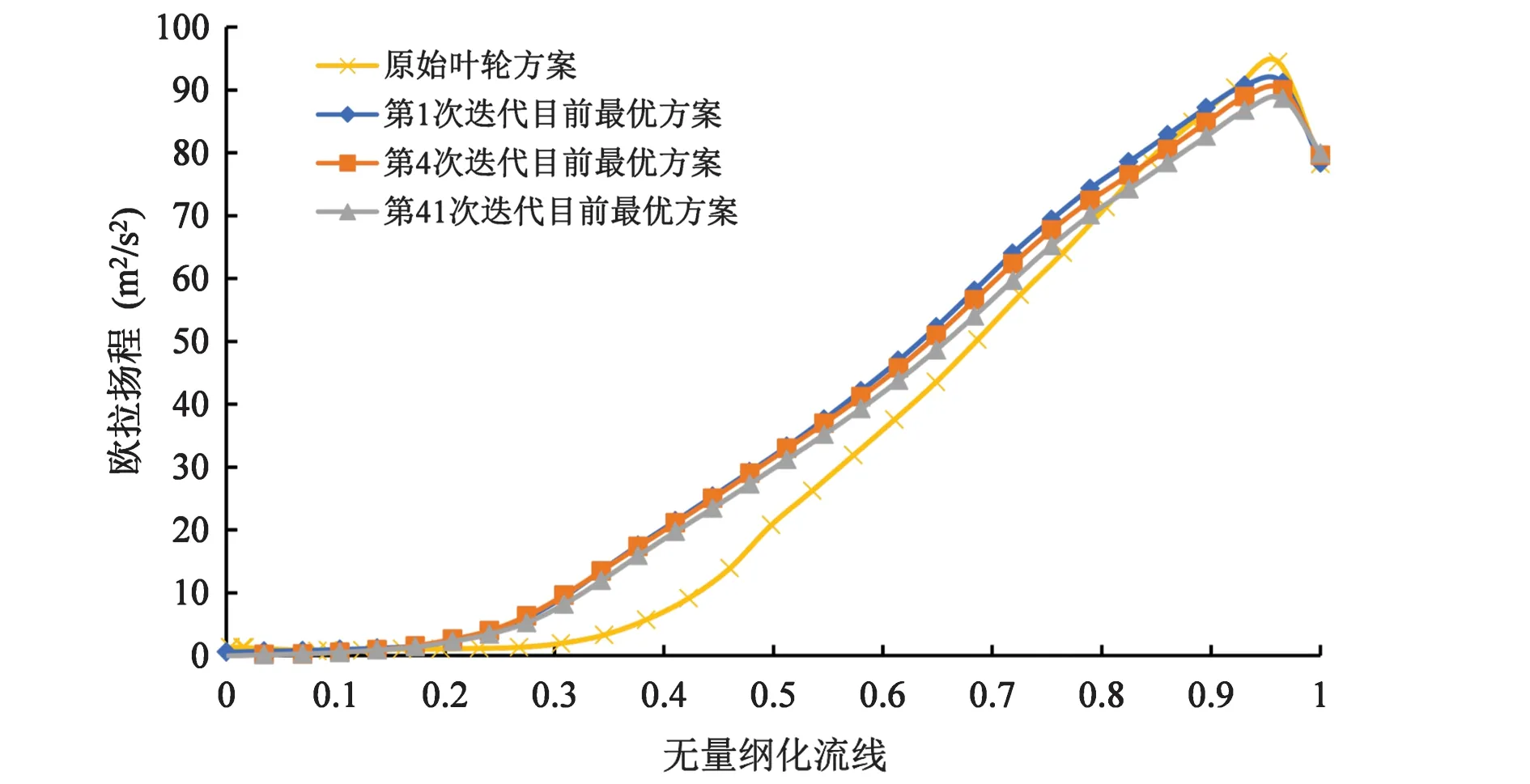
图12 叶轮从进口到出口欧拉扬程分布

从叶轮进口到出口的欧拉扬程(ucu/g)分布特性如图12所示.可以看出优化后的叶轮扬程在流线Streamline=0.2处开始上升，而原始叶轮扬程在流线Streamline=0.3处开始上升，优化的叶轮进口边位置比原始叶轮进口边更靠近叶轮进口，欧拉扬程快速增加，但变化梯度要比原始叶轮要小，有利于能量的转换.优化后的叶轮在叶片出口边处的欧拉扬程比原始叶轮偏小，但仍达到设计要求.

粒子群算法能成功解决多参数的泵性能优化问题，在今后的优化设计过程中，采用粒子群算法可以对叶轮和导叶的几何参数进行匹配 优化是必要的.

4 结 论

(1)基于改进的实时自适应粒子群算法，提出了一种带导叶离心泵叶轮自动性能优化方法.粒子群算法在搜索初期速度快，而在后期算法搜索趋于稳定.同时，设计变量也趋于稳定.在设计工况下优化的泵效率增加到78.50%，比原始方案的效率高2.1%；

(2)优化后的叶轮和导叶的内部速度流线分布得到改善，而且叶轮的欧拉扬程梯度小于原始方案，有利于减小水力损失；

(3)基于粒子群优化算法的带导叶离心泵叶轮多参数优化方法能在全局范围内寻找最优值，获得最优设计参数组合，对其他种类泵的性能优化具有借鉴意义，具有实际工程价值.