基于EMD-CNN的光伏逆变器开路故障诊断

孟献蒙，郭兴众，程凡永 ，陈旺斌，方骏仁

1 研究背景

近年来，随着石油、天然气等不可再生资源的日益消耗，越来越多的国家开始进行低碳能源转型[1]。在可再生、低碳能源生产中，太阳能光电技术显现出小规模能源生产的巨大潜力[2]。2005年以来，中国光伏制造产业发展迅速，并于2007年超过日本，成为世界上最大的光伏组件制造国[3]。截至2017年，中国、美国、印度、德国、日本等国家积极部署太阳能光伏产业，并已经在光伏市场中占主导地位[4]。未来太阳能光伏在全球各个国家低碳能源产业发展中继续具有重要的战略地位。而逆变器是光伏发电系统中的核心部件，其一旦发生故障，不仅会影响系统的正常运行，而且可能会对设备造成不可估量的损失。因此，开展光伏逆变器的故障诊断研究在设备损耗和降低成本投入以及逆变器保护等方面有着至关重要的意义。

目前，关于逆变器的故障诊断方法大体上可以分为如下3 类：基于参数辨识的方法、基于物理信号分析的方法和基于人工智能的方法。文献[5]通过对实测电流-电压（I-V）曲线进行参数辨识，以识别并且发现故障。文献[6]通过采集三相电压逆变器的输出电流信号，然后根据电流矢量的瞬时频率特征和瞬时角度特征的变化来进行故障诊断。文献[7-8]利用小波包分解和主成分分析法实现了故障诊断，其中，文献[7]基于极端学习机实现了单器件及多器件开路等多种故障诊断，文献[8]基于径向基神经网络对NPC 三电平逆变器开路故障进行了诊断。但是这些故障诊断方法都需要专业的物理知识和复杂的特征提取工程，不具备强的通用性。近年来，随着人工智能技术的发展，越来越多的深度学习技术被广泛地应用于逆变器的故障诊断中。文献[9]针对光伏组件中各种类型的故障，采用多层感知器来识别发生故障的类型和位置，但由于特征区分能力的限制，该方法不能有效地诊断不显著的故障类型。文献[10]为提高特征区分能力，采集了电压、电流和速度的变化信号，利用神经网络和遗传算法相结合的结构，对感应电动机电压源逆变器故障进行了诊断。尽管该方法提高了故障诊断率，但是需要3 个传感器采集数据，增加了设备的投入。

为减少传感器的使用数量和提高特征区分能力，本文提出一种基于经验模式分解（empirical mode decomposition，EMD）和二维卷积神经网络（twodimensional convolutional neural network，2D-CNN）结合的故障诊断方法。该方法首先使用一个传感器采集光伏逆变器的直流侧电流信号，采用EMD 提取电流中的多个本征模函数与原始数据组成的二维特征图作为2D-CNN 的输入；然后，利用2D-CNN 进行特征提取；最后，用2D-CNN 模型对多类开路故障进行诊断和分类。

2 光伏发电系统分析

2.1 光伏发电系统

光伏发电系统利用电池组件将太阳能直接转变为电能。在光照条件下，太阳电池组件产生一定的电动势，通过组件的串并联形成太阳能电池方阵，使得光伏阵列的电压达到系统输入电压的要求。光伏发电系统的主电路拓扑结构如图1 所示，左侧由光伏阵列产生直流输入，经过逆变器输出三相电流和电压。图中R、L分别是电阻和电感，C是电容，T1～T6 为6 个绝缘栅双极型晶体管（insulated gate bipolar transistors，IGBT），S1～S6 是6 个开关，系统通过调制电路来控制IGBT 的导通。

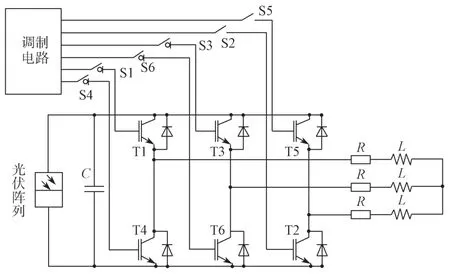
图1 光伏发电系统主电路拓扑结构Fig.1 Topological structure of main circuit of the photovoltaic power generation system

2.2 常见故障类型

逆变器的故障可以分为IGBT 短路故障和IGBT开路故障两类[11]。IGBT 短路因时间短暂可以在电路上直接进行处理，目前已经有相当成熟的解决方法[12]。当一个或两个IGBT 发生开路时，会导致逆变器不能正常导通。如果同一时间内有更多的IGBT开路，则此时逆变器早已不能正常工作，对于研究已无意义。因此文中的研究对象为一个或两个IGBT 开路故障。如图1 所示，当电路中一个开关断开的情况下，将会出现单管故障，共6 种情况（T1～T6 分别开路）。当电路中两个开关断开情况下，将会出现两管故障，而两管故障又分3 种情况：同一相的两个功率管开路故障，例如T1 和T4，共3 种；同一半桥的两个功率管开路故障，例如T1 和T3，共6 种；交叉的两个功率管开路故障，例如T1 和T6，共6 种。把正常情况归为一类，则IGBT开路故障的类型为22种。

3 多模态信号分解与特征提取

3.1 经验模式分解

经验模式分解（EMD），又可以称为Hilbert-Huang 变换（Hilbert-Huang transform，HHT）[13]，它是一种新型自适应信号时频处理方法。经验模式分解能够从单个信号中提取多尺度特征，特别适用于非线性、非平稳信号的分析处理之中[14]。EMD 能够使复杂信号分解为有限个本征模函数（intrinsic mode function，IMF）和一个残余项（res）之和，所分解出来的各IMF 分量包含了原信号的不同时间尺度的局部特征信号。

EMD 的基本分解流程如下：

1）获取原始时间序列x(t)的极值点；

2）采用三次样条插值函数拟合形成原数据的上包络x1(t)和下包络x2(t)，计算包络均值m(t)，

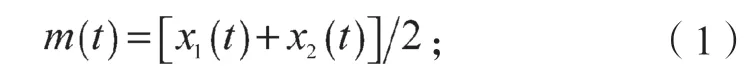
3）计算新序列h(t)，

4）判断h(t)是否满足IMF 的两个条件；

5）如果不是，则以h(t)代替x(t)，重复以上步骤，直到h(t)满足判据，则h(t)就是需要提取的IMF；

6）每得到一阶IMF，就从原信号中去除它，重复以上步骤，直到信号最后剩余部分就只是单调序列或者常值序列。

这样，经过EMD 分解，将原始信号x(t)分解成高频到低频的IMF 分量的线性组合和残余项r(t)；

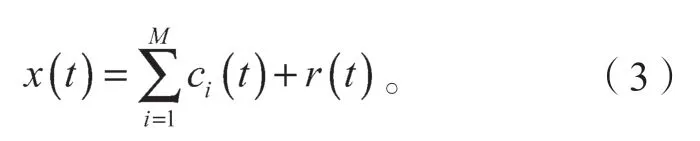
式中：ci(t)为第i个IMF 分量；

r(t)为残余项，不包含信号的震荡模态，只反映信号的变化趋势。

前面几个高频的IMF 分量包含了原始信号中显著且重要的特征信息。

3.2 卷积神经网络

3.2.1 卷积层

卷积层用到了数学运算-卷积，卷积是一种特殊的线性运算，用来替代一般的矩阵乘法运算。卷积运算的数学公式如下：

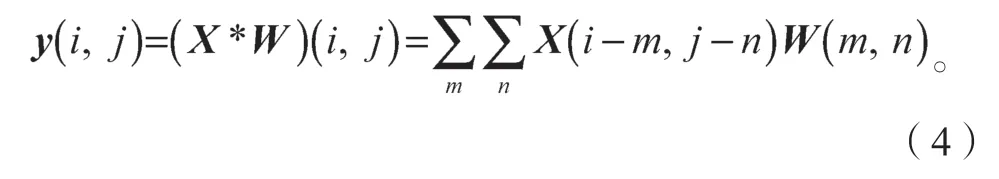
式中：X为二维矩阵；

W为权重参数，它可以是一个或多个二维矩阵；

y(i,j)为卷积运算的输出；

*为卷积运算符号。

在CNN 中，除了权重参数，还存在偏置。滤波器的参数就对应之前的权重。具体的卷积层运算如图2 所示，有一个3*3 的卷积核，卷积核都与输入信号进行卷积运算。卷积核滑动步长为1，卷积核为3*3，输入数据为4*4，经过卷积运算后，加上相对应的偏置，经过激活函数激活后就得到了大小为2*2的输出特征图。

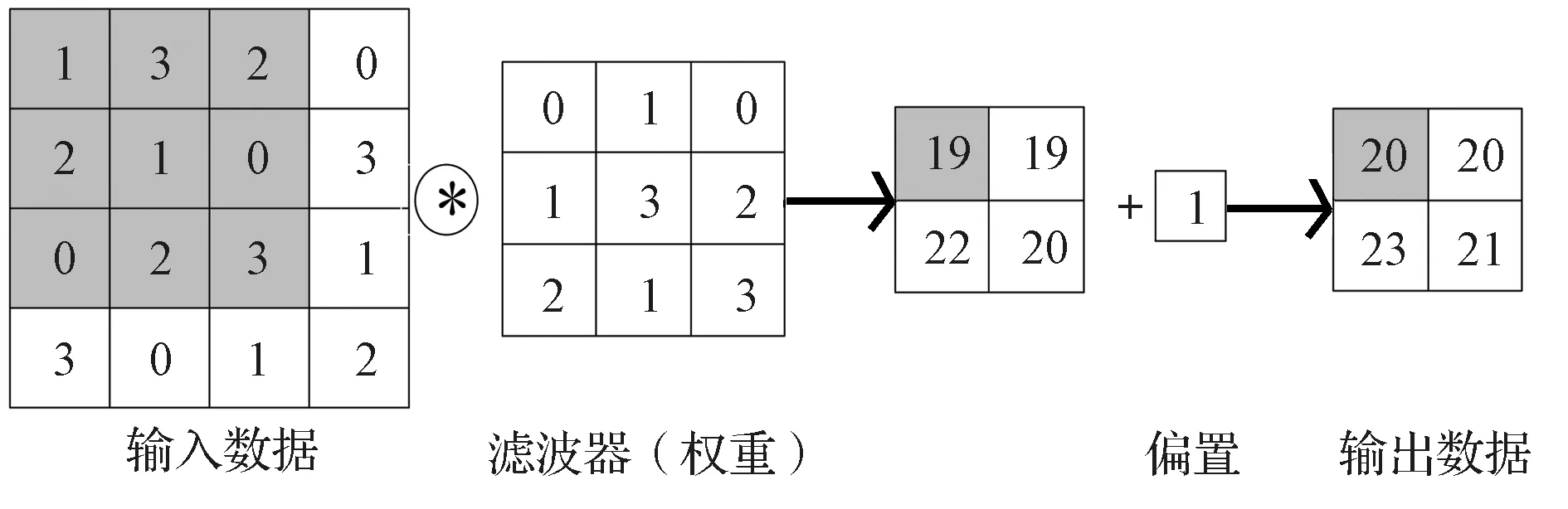
图2 卷积运算示例Fig.2 Illustration of convolution operation

3.2.2 池化层

理论上来说，所有经过卷积层获取的特征都可以直接输入到分类器中，但是巨大的计算量是一个难题。为了解决这个问题，一般会使用池化层来减少卷积计算中的冗余特征。池化层会将平面内某一位置及其相邻位置的特征值进行聚合统计（降采样），并且将聚合后的结果作为这一位置在该平面内的值。假设第l-1 层为池化层的上一层卷积层，第l层为池化层，则可以得到从第l-1 层到第l层的最大池化传播公式如下：

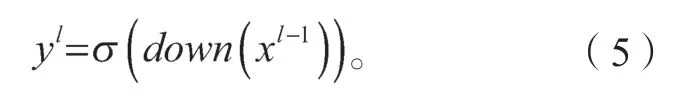
式中：down(·)为一个下采样方法，可以采用最大池化或平均池化；

σ(·)是激活函数。

图3 所示为最大池化层处理结果示意图，其中左侧图是原始的二维矩阵网格数据（深度为2，宽度和高度各为4），池化核的大小是2*2，并且池化核每次移动的步长是2。右侧图给出了网格数据经过最大池化之后的输出结果。

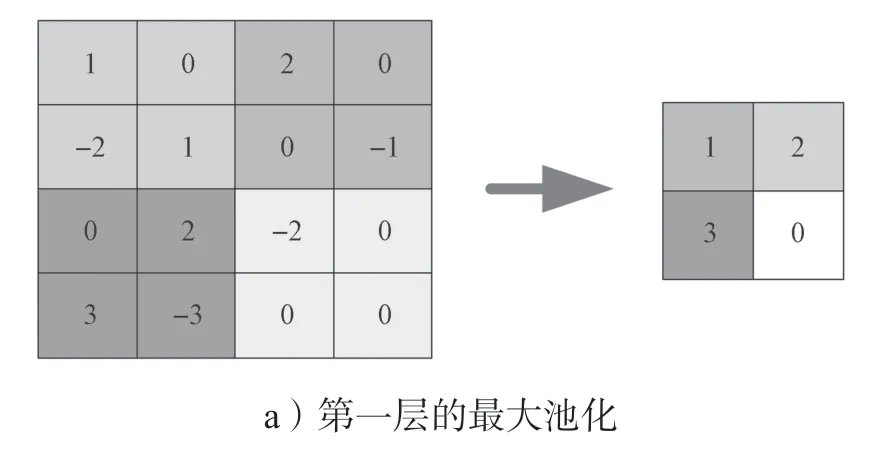
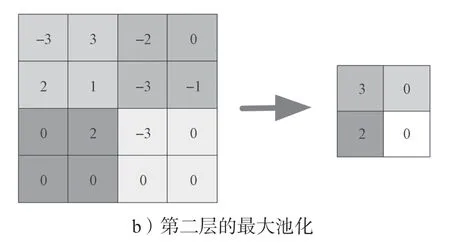
图3 最大池化层处理结果示意图Fig.3 Schematic diagram of the treatment results of the maximum pooling layer

3.2.3 全连接层

卷积层从输入中提取特征，这些特征经过池化层处理后被输入到一个全连接层中进行分类。全连接层的计算公式为

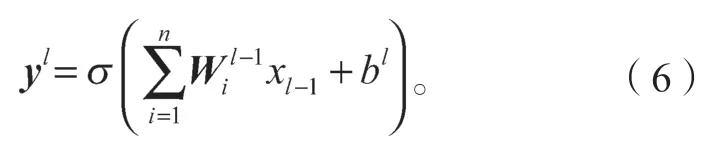
式中：yl为第l层的输出；

bl为第l-1 层的所有神经元到第l层的所有神经元集合的偏置；

σ(·)为激活函数。

4 基于 EMD-CNN 的故障诊断方法

4.1 EMD 分解和2D-CNN 模型

为了确定IMF 的个数，本研究中对5 类开路故障中的一种故障数据分别进行了EMD 分解，每一种故障数据的序列长度为200，所得到的实验结果如图4 所示。所设计的二维卷积神经网络模型（2D-CNN）如图5 所示，由输入层、3 个卷积-池化模块、平铺层、全连接层、Softmax 层和输出层构成。

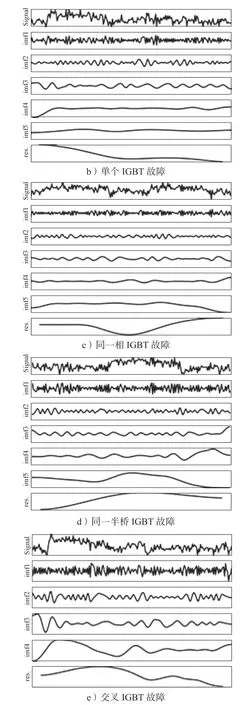
图4 5 类开路故障数据的EMD 分解Fig.4 EMD of five types of open-circuit fault data

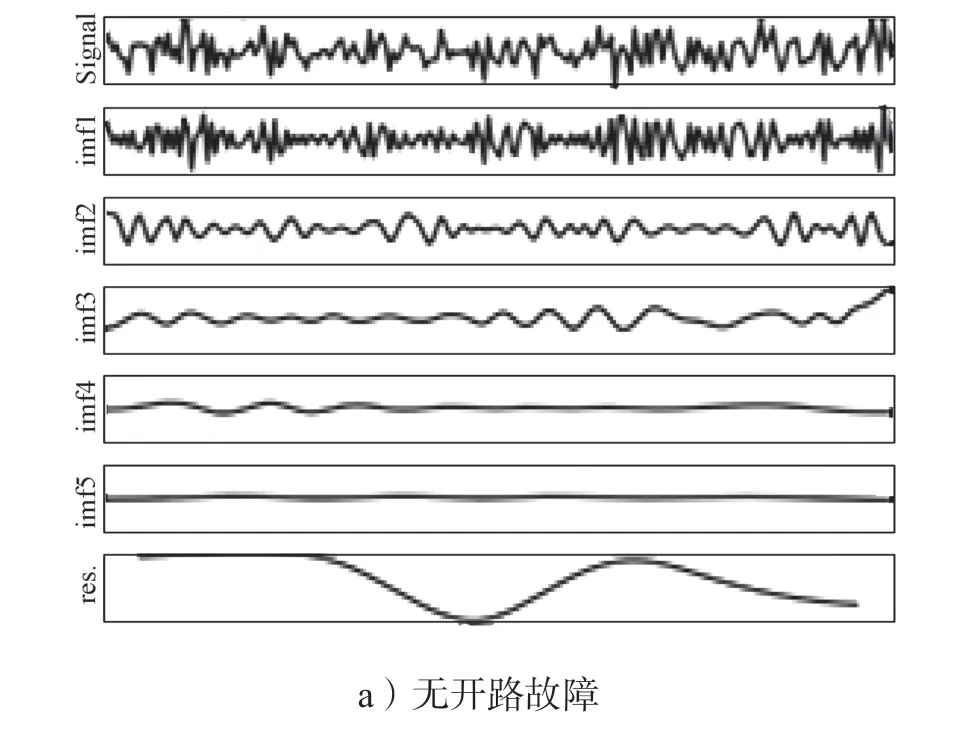
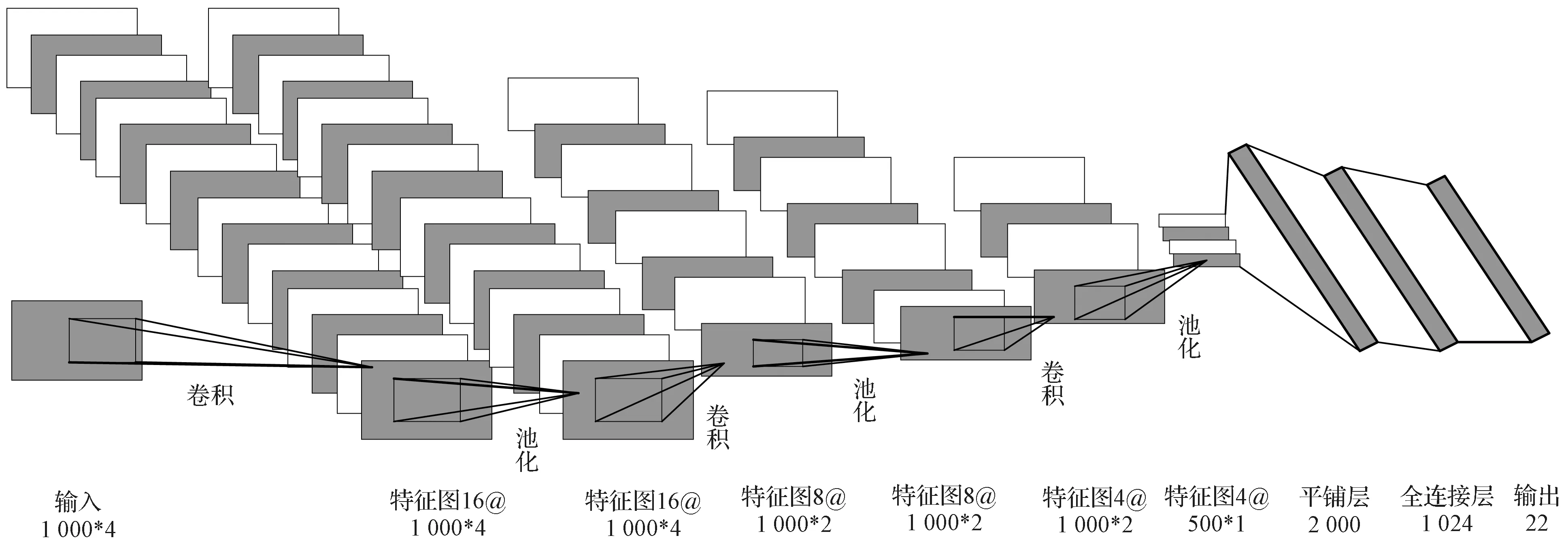
图5 2D-CNN 模型示意图Fig.5 2D-CNN model diagram

4.2 诊断方法

基于EMD-CNN 的故障诊断方法如图6 所示。

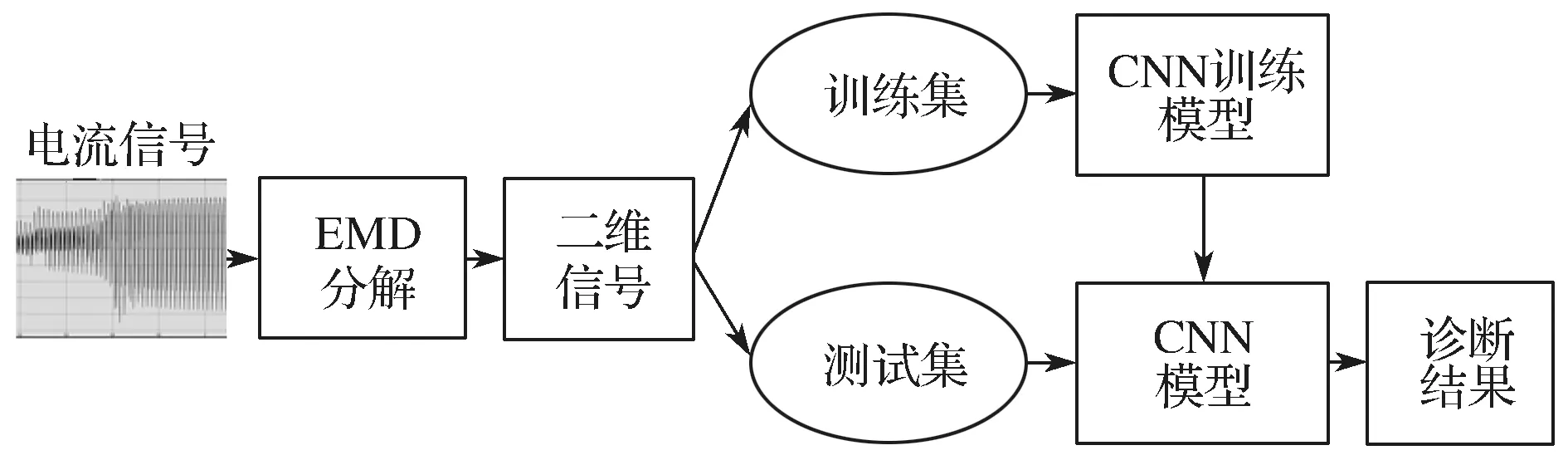
图6 基于EMD-CNN 的故障诊断方法Fig.6 Fault diagnosis method based on EMD-CNN

基于EMD-CNN 的故障诊断的具体步骤如下：

1）控制开关的闭合来模拟光伏逆变器的IGBT开路故障，并利用传感器采样电流信号；

2）设置IMF 的个数，对电流信号进行EMD 分解，得到各开路故障下的IMF 分量；

3）组合IMF 和原始数据，获取不同开路故障下的特征向量样本；

4）将故障数据集分为训练集和测试集，利用训练集训练EMD-CNN 故障诊断模型；

5）把测试集输入训练的EMD-CNN 中进行故障识别和诊断。

5 实验结果与分析

5.1 数据的采集和分割

本研究中所设计的光伏发电系统的仿真模块如图7 所示。图7 所示仿真模块具有最大功率点跟踪和电压前馈控制功能。在仿真中，采样频率设置为104Hz，总运行时间为4.1 s，电阻为0.1 Ω，电感为0.002 H，三相电流频率为50 Hz。前0.1 s，系统刚刚通电，数据的波动巨大，所以舍去这一部分的数据，数据采集的时间为0.1～4.1 s。此外，当采样过程执行到0.25 s 时，系统的工作条件发生变化，光照强度从700 W/m2变为1 000 W/m2。这样做的目的是更加符合光伏逆变器的实际工作环境。从图中可以看出，6个IGBT 分别连接了一个开关。数据集的获取方法如下：人为地控制不同开关的闭合，利用传感器以数据段的形式等时间采样每一种情况下（22 种）的直流侧电流信号，每种故障的采样数为2 000 个，总共收集了20 个数据段，最后经EMD 分解后，汇总成440个样本的数据集。

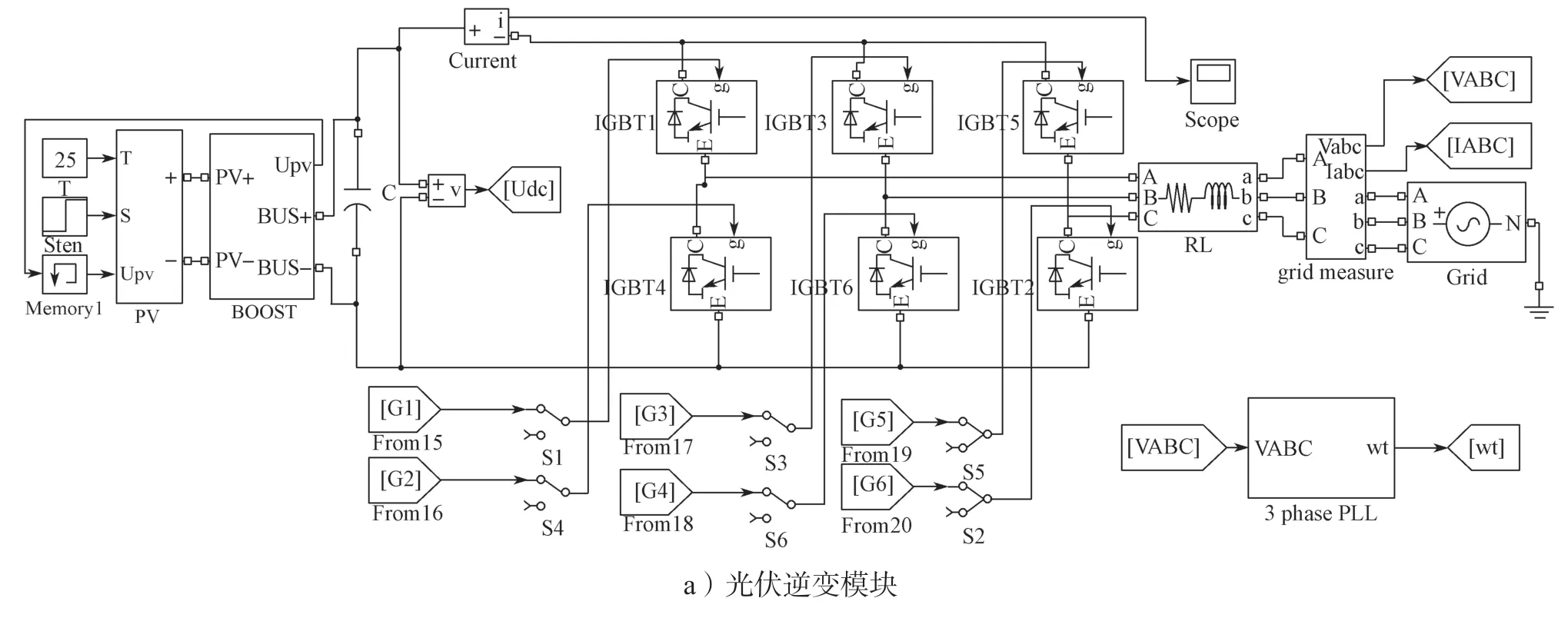
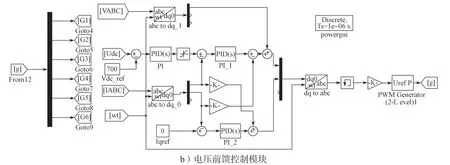
图7 光伏逆变系统的仿真模块Fig.7 Simulation of the photovoltaic inverter system

每个故障样本数据序列长度为2 000 个，它仍然是一个长的一维时间序列数据。在2D-CNN 模型训练过程中，如果把这个长的一维时间序列数据经过EMD 处理后一次性输入2D-CNN 模型中，会带来很大的计算复杂度。为了解决这个问题，对数据采用了分段分割[15]。根据采样周期，长的一维时间序列数据可以被分割成若干个等长度的短一维时间序列数据段，并将短的一维时间序列数据段作为一个故障样本。为了提高相邻样本之间的相关性，文中采用了滑动窗口重叠采样方法[16]。通过这种方法，可以获得更多的故障样本用于2D-CNN 诊断模型的训练和测试。

图8 所示为数据分割的重叠采样法示意图。

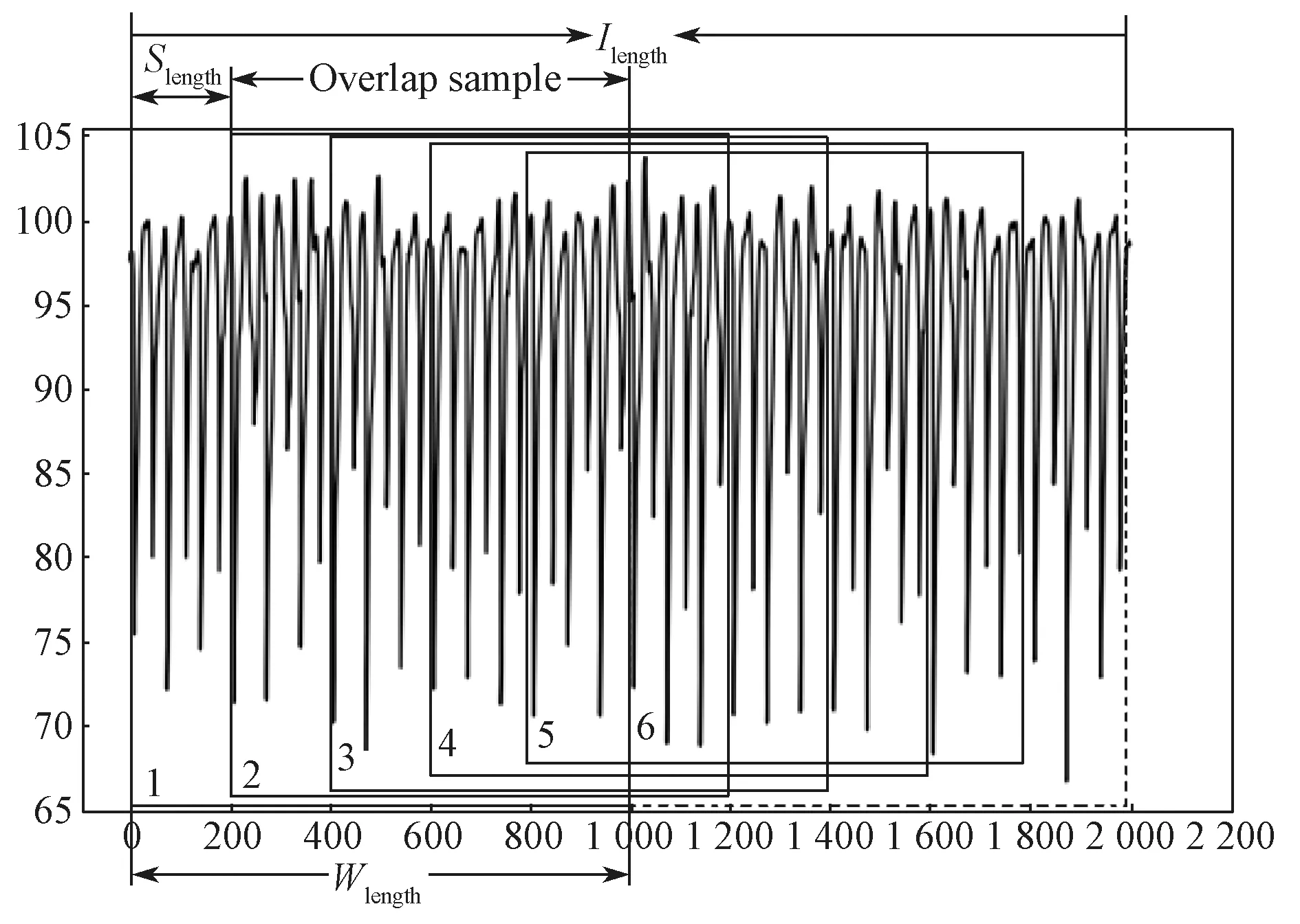
图8 数据分割的重叠采样法Fig.8 Overlapping sampling method for data segmentation

在图8 中，长的一维时间序列数据段有2 000 个数据。采用滑动窗口重叠采样方法，即每一次向前移动200 个数据，这样就可以得到6 个新的样本。每个新样本的长度为1 000 个数据。重叠样本的数据点数量为800 个，重叠率为80%。重叠采样的样本量计算方法定义如下[17]：式中：Samplenum为利用重叠采样法得到的新故障样本量；

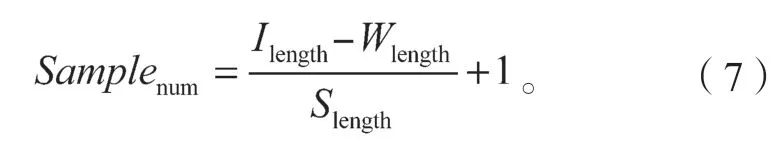
Ilength为原始数据段的数据点数量；

Wlength为滑动窗口内数据点的数量；

Slength为检测步长的数据点数量。

本研究中，Ilength为2 000 个数据，Wlength为1 000个数据，Slength为200 个数据。因此，根据公式可以计算出图8 的Samplenum为6。

5.2 模型参数的设置

在仿真实验中，光伏逆变器的直流侧电流信号是在理想状态下获取的，它不受外界因素的影响。为了保证数据的有效性，人为地在数据上加入了不同信噪比（signal noise ratio，SNR）的噪声，SNR 的计算公式如下：SNR=10 lg(Ps/Pn)。 （8）

式中：Ps为信号的有效功率；Pn为噪声的有效功率。

在模型训练过程中，参数设置对网络模型的性能有重要影响。检测步长是网络模型中的一个重要参数，它代表模型中数据的更新数量。5 dB 噪声下不同检测步长的诊断准确性以条形图显示，如图9 所示。

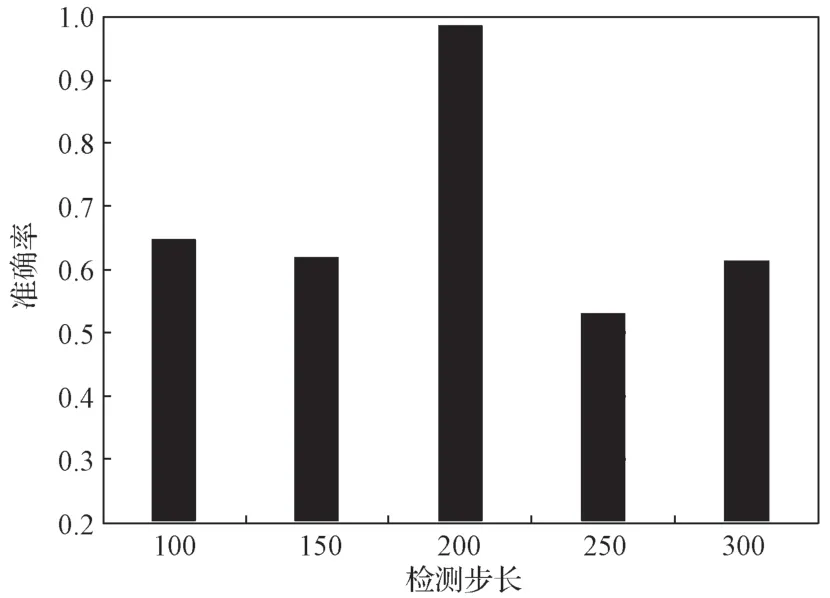
图9 不同检测步长的故障分类准确率Fig.9 Fault classification accuracy rate ofdifferent detection steps

由图9 可知，当检测步长设置为200 个数据时，故障诊断的效果最佳，准确度达到了0.987 4。同时，200 个数据的采样时间正好为0.02 s，这与相电流的周期保持一致。因此，文中的后续实验将检测步长设置为200 个数据。

滑动窗口代表每一次输入网络模型的数据样本个数，其数值的改变将会影响模型的故障诊断和分类。实验过程中设置了5 种滑动窗口，其数据量分别为400, 600, 800, 1 000, 1 200。5 种噪声下的故障诊断准确率如图10 所示。

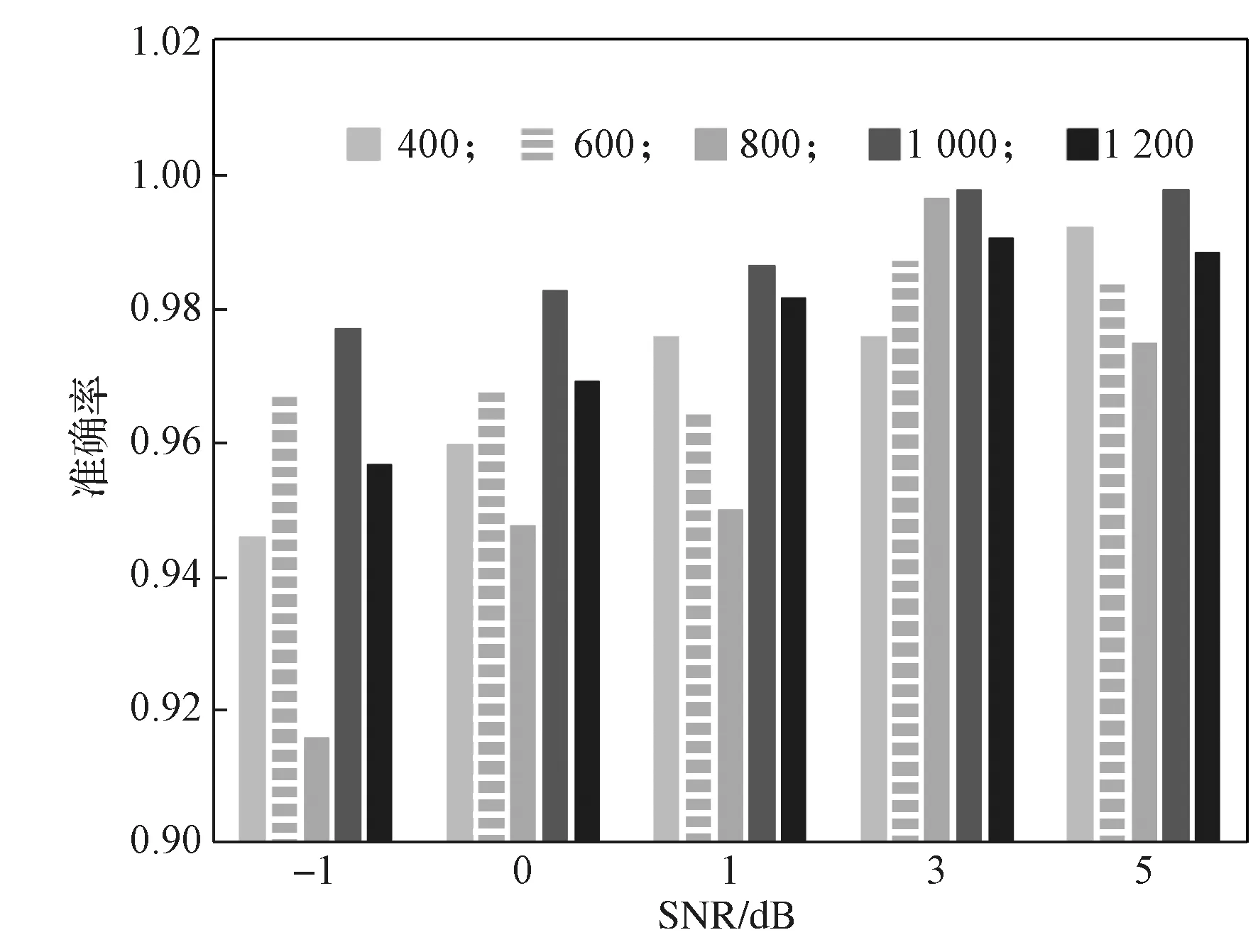
图10 不同噪声下5 种滑动窗口的故障分类准确率Fig.10 Accuracy rate of the fault classification of five sliding windows under different noises

由图10 可知，相较于另外4 种滑动窗口，当滑动窗口为1 000 个数据时，5 种噪声下的故障诊断准确率均最高。因此，当滑动窗口为1 000 个数据时，故障的分类效果最好。

5.3 实验对比

选择kNN（k-nearest neighbor）[18]、SVM（支持向量机）[19]和CNN 方法进行对比实验。

1）kNN 方法。在实验中，kNN 的超参数n_neighbor 设置为7。

2）SVM 方法。实验中采用线性核支持向量机对逆变器数据进行故障诊断。

3）CNN方法。将输入数据变形为[400，1]的形状，并输入CNN 网络，最后通过Softmax 层输出故障诊断结果。

在实验中，批量大小设置为600 个数据，学习率设置为0.000 1。所得4 种方法的故障诊断结果如表1所示。从表1 中的数据可以得知，EMD-CNN 的诊断精度均优于前3 种方法。最重要的是，EMD-CNN 在5 种不同级别的噪声上均具有最佳性能。这主要是由于EMD 对故障数据进行了多尺度分解，CNN 可以快速且精准地对故障数据进一步提取特征，最后实现故障的诊断和分类。因此，EMD-CNN 在处理光伏逆变器的IGBT 开路故障和获得最佳故障诊断性能方面具有明显的优势。

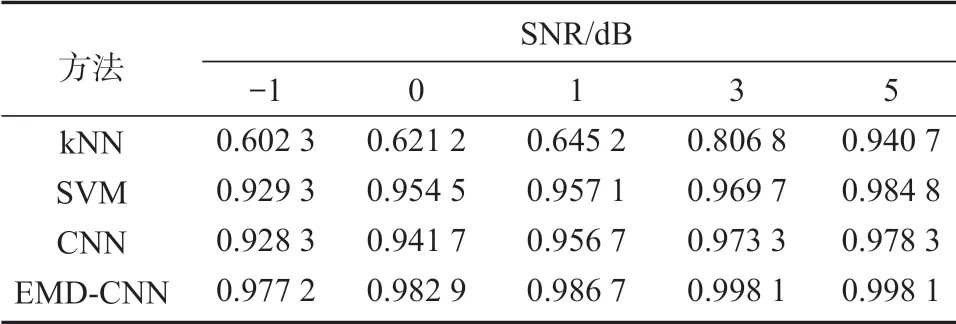
表1 不同噪声下不同方法的故障诊断准确率Table 1 Accuracy rate of different methods under different noises

6 结语

本文提出了一种结合EMD 和CNN 的光伏逆变器故障诊断方法，利用直流侧电流对开路故障进行监测。并且对光伏逆变器系统进行了Simulink 仿真，以验证所提出方法的性能。为了测试该方法的鲁棒性和适用性，将不同强度的高斯噪声人工添加到数据集中。实验结果表明，与传统的分类方法相比，该方法在不同噪声水平下可以获得更高的故障诊断精度。

后续研究中，为了充分利用CNN 进行直流侧电流的深度特征提取能力和LSTM 在处理时间序列数据上的优异性能，值得研究CNN-LSTM 的组合模型，以进一步提高在较高噪声水平下的故障诊断性能。