一种新型开关模式的高增益低谐波三相逆变器

2021-11-01吴方礽王军章廖晓斌曾进辉

湖南工业大学学报 2021年5期

兰征，吴方礽，王军章，廖晓斌，刘湘，曾进辉

1 研究背景

随着电力电子技术的不断发展，DC/AC 逆变器现已经被广泛地应用于电源、新能源发电、电机驱动、不间断电源等电气领域[1-2]。在各种逆变器拓扑结构中，基于桥式结构的三相逆变器，具有结构简单、控制灵活、既能并网运行又能离网运行等优点，得到了广泛的研究。逆变器的直流电压利用率和输出电压谐波是很重要的性能指标，直流电压利用率的高低将直接影响整个逆变器系统的运行效率。某些高端设备、精密仪器等负荷，要求逆变器输出电压具有较低的谐波畸变率[3]。然而现有三相桥式逆变器的直流电压利用率提升能力有限，减少谐波含量的方法也有一定的局限性，因此三相桥式逆变器不太适用于这些特殊应用场景。

采用正弦脉冲宽度调制SPWM（sinusoidal pulse width modulation）的三相逆变器，理论上能够达到的最大直流电压利用率仅为0.866[4]。文献[5]分析了空间矢量脉冲宽度调制SVPWM（space vector pulse width modulation）方法，与SPWM 相比，SVPWM可以将直流电压利用率提升15.47%。文献[6]通过在三相无中线系统的相电压调制信号中注入3 次谐波，也使得直流电压利用率提升了15.47%。提高直流电压的利用率能够提高逆变器的带载能力，减小功率器件的电压应力[7]，但是基于PWM（pulse width modulation）调制的桥式逆变器，理论上其最大直流电压利用率为1，提升能力有限。

为减小逆变器输出电压的谐波畸变率，文献[8-11]提出了多电平变换器，该类型变换器交流侧电压的电平数不小于3。逆变器输出的电平数越多，电压波形越接近于正弦波，谐波含量越少。但是，多电平变换器的系统结构和控制方法相对而言较为复杂，可靠性和稳定性较差[12]。另外，有学者提出采用LCL 型滤波器以减少逆变器的输出谐波含量[13]，但是LCL 型滤波器容易引起谐振尖峰问题[14]，降低了系统的稳定性。

本文提出一种新型开关模式的高增益低谐波三相逆变器。首先，介绍了其拓扑结构，并且详细分析了其工作原理和开关模式；然后，将准PR（quasiproportional resonance）控制引入其中，实现了对逆变器的恒压恒频控制，并且分析准PR 控制参数对逆变器输出性能的影响；最后，在Matlab/Simulink 中搭建了该仿真模型，给出仿真验证分析结果。仿真结果表明，该新型开关模式三相逆变器的最大直流电压利用率为1.73，谐波含量也低于常规桥式三相逆变器，从而验证了所提新型开关模式的三相逆变器及其控制策略的正确性和有效性。

2 拓扑结构与工作原理

2.1 拓扑结构

逆变器通常由斩波电路和逆变桥电路组成[15]，属于两级式结构的逆变器，本研究中所提出的新型三相逆变器的拓扑结构如图1 所示。图1 中：Vs为输入直流电源，L、C分别为滤波电感和电容，Q11～Q34为开关管。

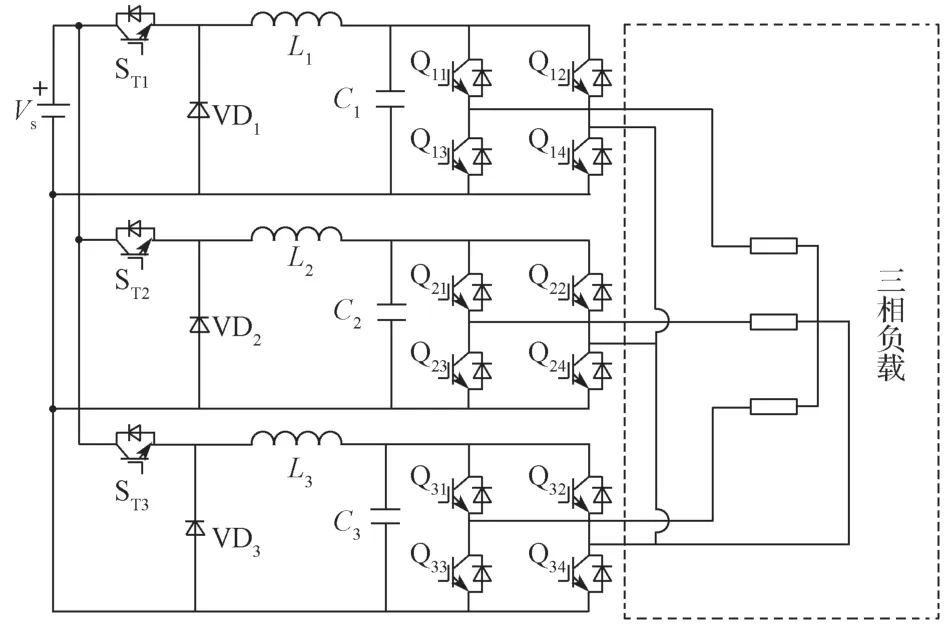
图1 新型三相逆变器的拓扑结构Fig.1 Topology of the new three-phase inverter

逆变器每一相的前端为Buck 变换器，后段为H桥，如图2 所示，其稳态输出电压为

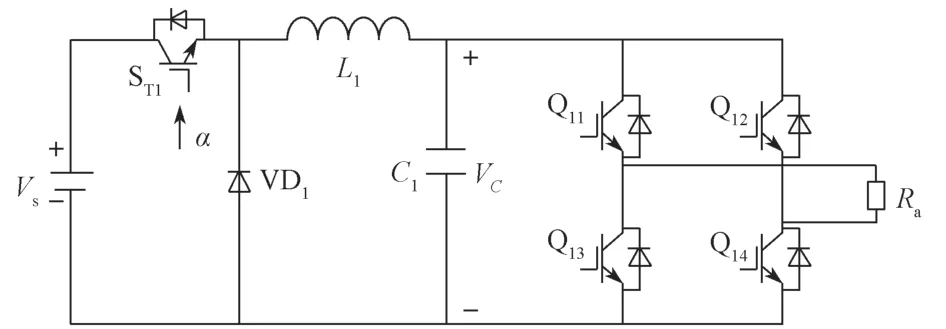
图2 单相新型开关模式逆变器Fig.2 New single-phase switching mode inverter

式中：α为Buck 变换器功率开关管的导通占空比；

Vs为输入直流电压。

直流电源电压恒定，通过控制开关频率的变化来使得占空比α随着直流脉动（如图3a 所示）呈规律变化，即

所以在功率开关管ST1输出端的输出电压为等效正弦正半波的PWM 波，如图3b 所示。电压通过Buck 电路中的LC 滤波器后，输出的只有正弦正半周的直流脉动波形，如图3c 所示。后面跟随的H 桥与50 Hz的工频信号同步。通过Q11/Q14与Q12/Q13交替导通，将直流脉动波变换成标准的正弦波，如图3d 所示。

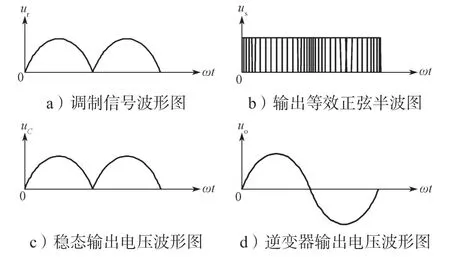
图3 主要原理波形示意图Fig.3 Schematic diagram of main principle waveforms

虽然此种新型三相逆变器的开关器件较多，但是工作在高频的功率开关管只有ST1、ST2、ST33 个，其余H 桥电路的开关管的工作模式为零电压开通和零电流关断，即软开关状态，几乎不产生损耗。而逆变器的开关损耗主要来自高频开关，新型三相逆变器的高频开关数量是传统的三相桥式逆变器的一半，因而大大降低了开关损耗。

2.2 工作原理

2.2.1 原理分析

若ST1、ST2、ST3的PWM 波形都随着直流脉动波变化，并且其相位相差120°，由式（2）可以得知，图1 中的功率开关管ST1、ST2、ST3的导通占空比也均随着直流脉动波发生变化，且其相位相差120°，因此三相逆变器当中ST1、ST2、ST3的占空比分别如下：

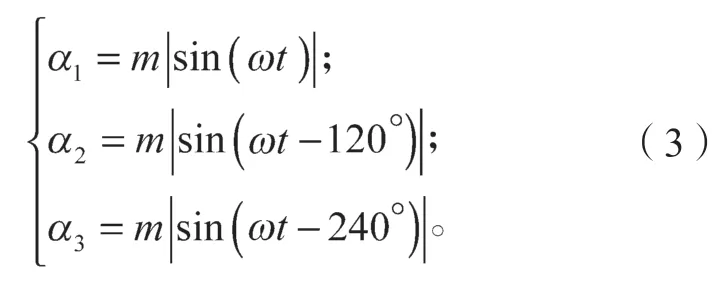
式中m为调制系数，其表达式为m=Vo/Vs，其中Vo为逆变器输出电压，Vs为输入直流电压。

当系统达到稳态时，三相逆变器的Buck 变换器输出侧电压如下：

结合式（3）可得：

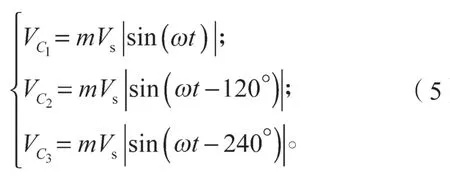
从式（5）可以看出，三相Buck 电路输出端电容上所加电压、、都只含有正弦的正半周波形，这是一直流量，因此电容C1、C2、C3均可以按照直流型（如电解电容器）进行设计。然而，传统的桥式逆变器和PWM 逆变器中的滤波电容上的电压都是交流量。与传统逆变器相比，相同容量大小的滤波电容，直流型的滤波电容体积较小、价格较低，但是滤波效果更好，滤波器输出电压谐波含量更少[16]。随后H 桥的4 个开关管Q11/Q14与Q12/Q13以50 Hz 的频率交替导通。比如在t=0 时，Q11/Q14导通，Q12/Q13关断；t=T/2 时，Q11/Q14关断，Q12/Q13导通；其余B、C 两相类似。变换后的输出电压如下：

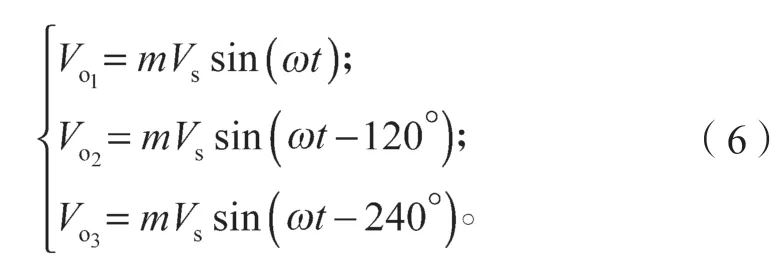
式（6）表明，输出电压是一光滑的正弦波，实质上是由Buck 变换器中的高频开关ST1、ST2、ST3不断改变开关频率，使得输出电压等效为含有无限电平数的正弦波形，输出电压波形中电平数的增加在很大程度上降低了谐波。

每一相H 桥中的4 个开关管不但工作频率很低（50 Hz），而且都工作在软开关状态，因此几乎不产生损耗。式（6）中的电压是相位互差120°的相电压，最大的相电压峰值为Vs。当三相对称时，由式（6）可以推导出线电压如下：

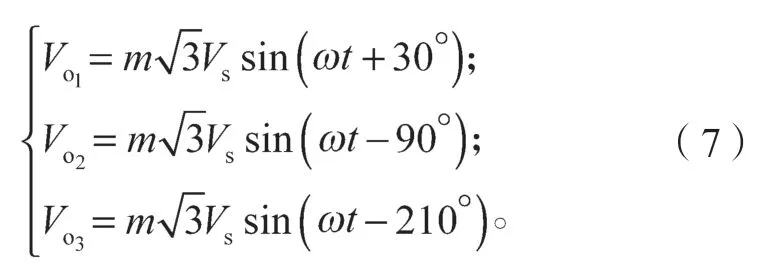
式中：Vl为输出线电压峰值；

Udc为直流电源电压。则该新型开关模式逆变器的最大直流电压利用率为≈1.73。然而传统桥式三相逆变器采用SPWM 调制时，其最大直流电压利用率只有0.866。即使采用SVPWM 调制或三次谐波注入法，能获得的最大直流电压利用率也只有1[17]。可见，该新型开关模式三相逆变器与现有桥式三相逆变器在直流电压利用率方面有显著的优势。

2.2.2 开关模式分析

正常运行状态下，每一相的5 个功率开关管都有4 种开关模式，且每一种开关模式对应不同的开关回路。为了详细分析每种开关模式的功能，以A 相为例，给出各开关模式下的电流回路以及等效电路图，如图4 所示。

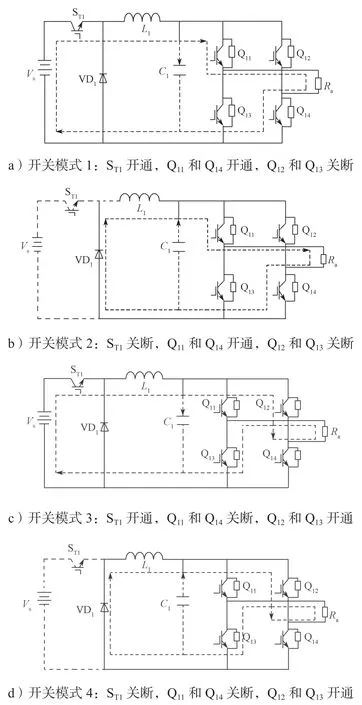
图4 各开关模式的等效电路图Fig.4 Equivalent circuit diagram of each individual switching mode

开关模式1 时（如图4a）：ST1开通，Q11和Q14开通，Q12和Q13关断。此时电流通过Vs、ST1、L1、Ra、Q11和Q14形成回路，同时直流电源给电容C1充电，给负载供电。

开关模式2 时（如图4b）：ST1关断，Q11和Q14开通，Q12和Q13关断。此时电流通过VD1、L1、Ra、Q11和Q14形成回路，同时电容C1放电，VD1起到续流作用。

开关模式3 时（如图4c）：ST1开通，Q11和Q14关断，Q12和Q13开通。电流通过Vs、ST1、Ra、Q14和Q13形成回路，此时直流电源为电容充电，为负载供电。

开关模式4 时（如图4d）：ST1关断，Q11和Q14关断，Q12和Q13开通。此时电流通过VD1、L1、Q14、Ra和Q13形成回路，电容C1放电，VD1续流。

Buck 变换器后面跟随的H 桥由4 个开关管（Q11～Q14）组成。H 桥实现随着参考电压同步逆变翻转的功能，如图5 所示。

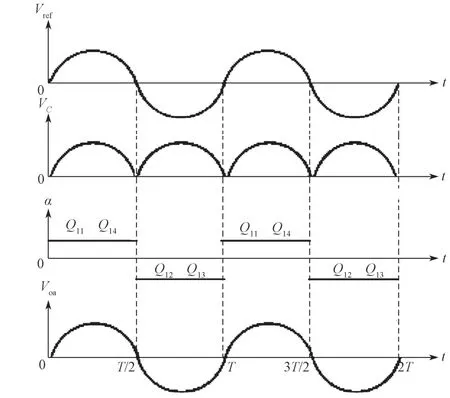
图5 H 桥的开关工作方式Fig.5 Operation mode of H-bridge switches

在0～T/2、T～3T/2 等时间段内，开关管Q11和Q14处于导通状态，开关管Q12和Q13处于关断状态；在T/2～T、3T/2～2T等时间段内，开关管Q12和Q13处于导通状态，开关管Q11和Q14处于关断状态。因此将Buck 变换器输出侧电容电压VC翻转为标准的正弦输出电压Voa。

3 控制策略与参数设计

3.1 准PR 控制

传统的PI 控制器由比例和积分环节组成，其传递函数为

式中：kp和ki为PI 控制器的参数；

s为复频率。

控制器在基波频率ω0处的增益为

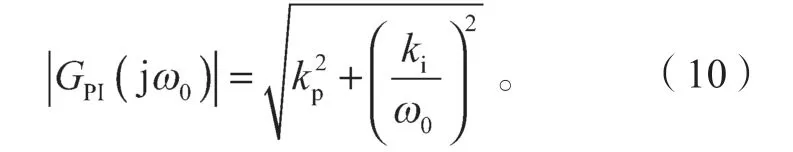
式中j 为虚数单位。

从式（9）和式（10）中可以看出，PI 控制器是一种线性控制器，在基频处的增益为一有限定值，因此只能对直流量进行准确跟踪。若要将PI 控制应用于三相交流，必须进行复杂的abc/dq或αβ/dq坐标变换，将交流量变化成直流量，才能实现无静差跟踪控制。

为了克服PI 控制器的缺陷，很多文献提出了采用PR 控制器[18-19]，其传递函数如下：

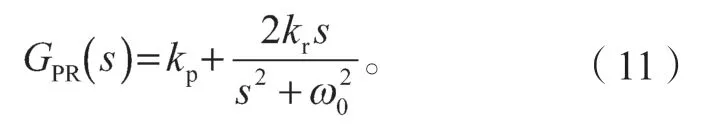
将基波频率ω0代入PR 控制器的传递函数式（11）中，可以得到其在基波频率ω0处的增益为

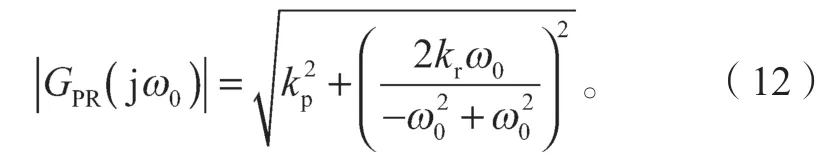
通过根轨迹法分析可知，PR 控制器相比PI 控制器，传递函数在s平面的虚轴上增加了2 个固定频率的闭环极点形成谐振，使得PR 控制器在基波频率处的增益趋近无穷大，从而可实现该频率下交流量的无静差控制[20]。

相比PI 控制器，PR 控制器理论上在特定频率处的增益为无穷大，能实现对特定频率的交流量的无静差控制。在对电流内环控制设计中，无需复杂的dq坐标变换，也没有dq轴之间的耦合关系，从而简化了控制系统设计。但是，在实际电网中，电网频率有一定的波动，理想的PR 控制器的带宽比较窄，无法适应实际波动的电网。为了解决这一问题，引入准PR 控制器，其传递函数为

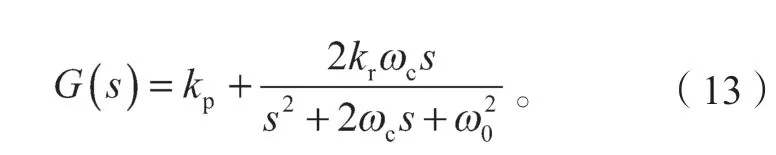
相比于PR 控制器，准PR 控制器相当于在PR控制器的传递函数中增加了一个零点，从而增加了控制器的带宽，因而更能适应实际频率波动的电网，可有效解决由于频率波动引起逆变器控制性能变差的问题。

3.2 控制参数分析

由式（13）可以得出，准PR 控制器的传递函数含有kp、ωc、kr3 个变量。为了研究每个参数对逆变器输出性能的影响，此处使用控制变量法分析3 个变量对系统性能的影响。

1）设定kp=1、ωc=1，kr为变量，画出相应传递函数的伯德图（如图6 所示），以研究kr对控制器性能的影响。从图6 中可看出，随着kr参数的增大，控制器的增益也增大，然而控制器的带宽却没有变化。因此，kr参数只影响控制器的增益，而不影响控制器的带宽。

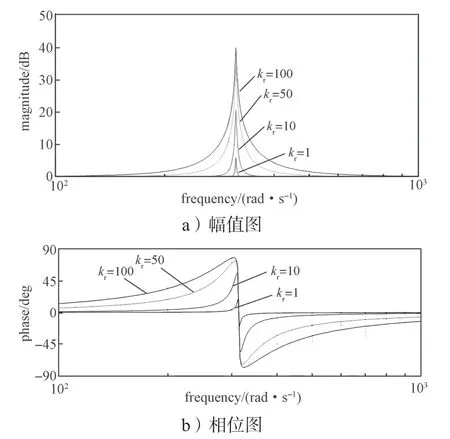
图6 kr变化时，准PR 的bode 图Fig.6 Bode diagram of quasi-PR with changes of kr

2）设定kp=1、kr=1，ωc为变量，画出相应传递函数的伯德图（如图7 所示），研究ωc对控制器性能的影响。

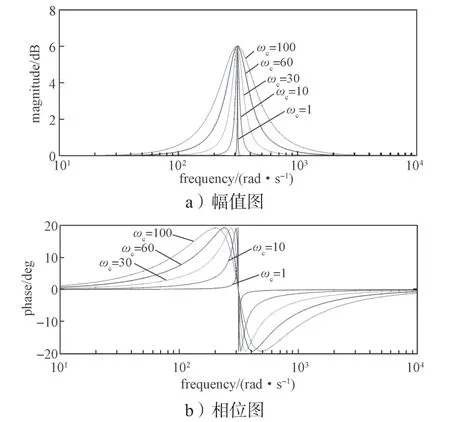
图7 ωc变化时，准PR 的bode 图Fig.7 Bode diagram of quasi-PR with changes of ωc

由图7 可以看出，随着ωc参数的增大，控制器的增益和带宽都增大，但是在基频处的增益却没有变化。可见，ωc不仅会影响控制器的增益，还会影响带宽，因此在选择ωc参数时不能一味追求大的带宽，因为ωc越大，虽然带宽增大，但是在基频较远处的谐波也会被放大。

3）设定ωc=1、kr=1，kp为变量，画出相应传递函数的伯德图（如图8 所示），研究kp对控制器性能的影响。

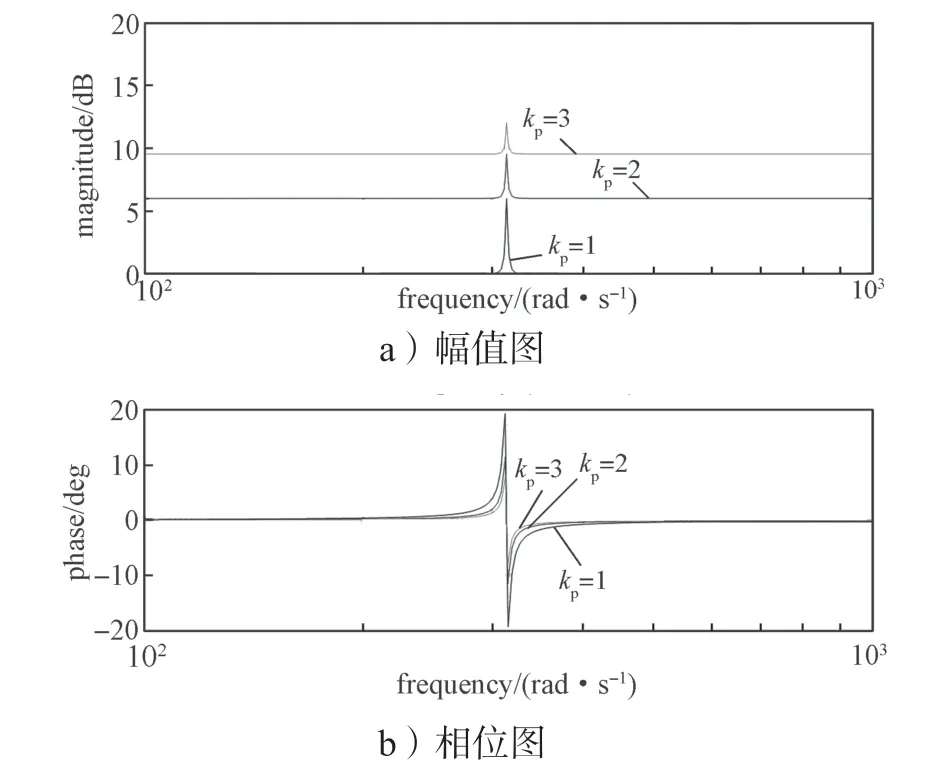
图8 kp变化时，准PR 的bode 图Fig.8 Bode diagram of quasi-PR with changes of kp

从图8 所示传递函数的伯德图中可以看出，参数kp影响了所有频率处的增益，它影响着整个控制系统的整体性能。因此在设置PR 控制器参数时，应综合考虑稳态性能以及各参数之间的相互影响关系等因素，确定最终参数。

3.3 总体控制策略

为简化说明总体控制策略，以A相为例进行说明，新型三相逆变器每相控制策略见图9，其余B、C 两相类似，只是给定的参考信号相位互差120°。

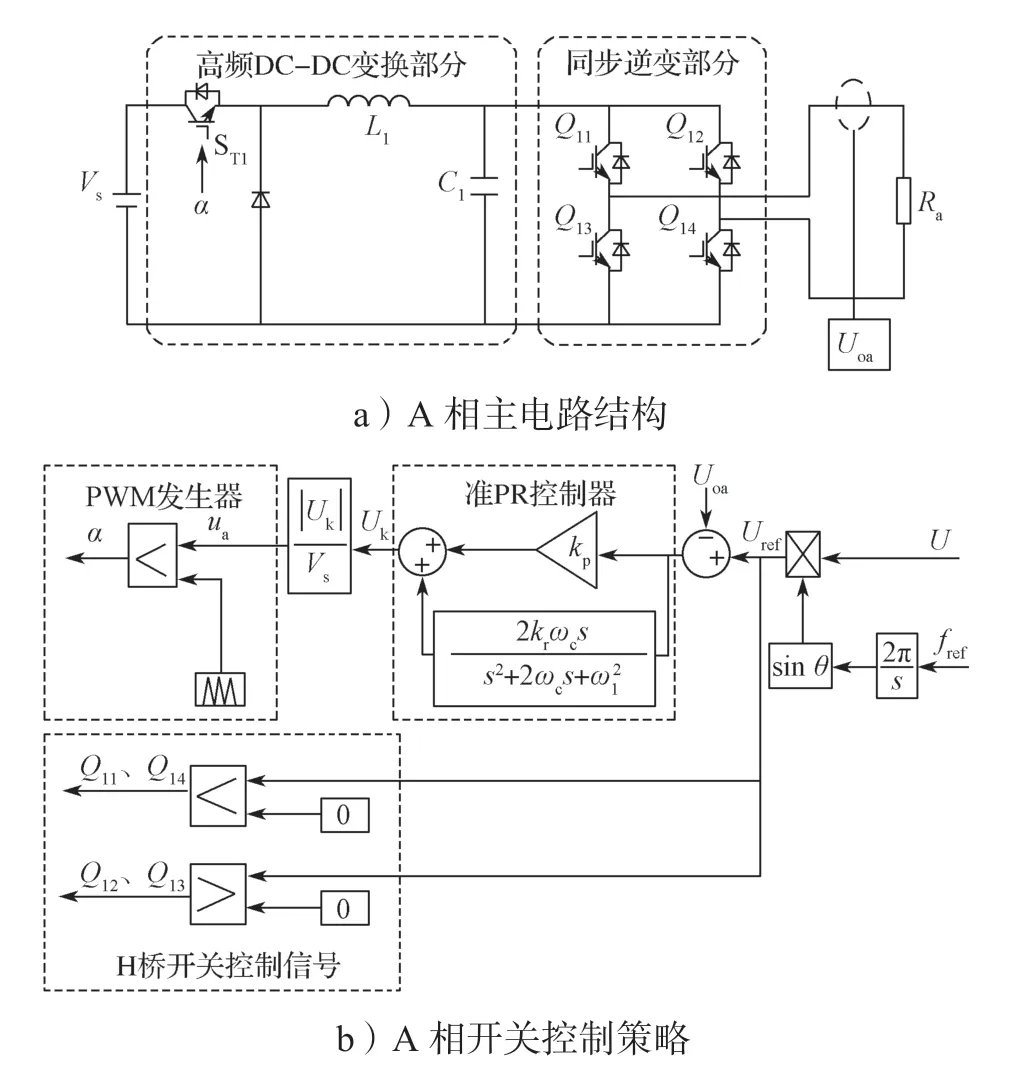
图9 新型三相逆变器的控制策略Fig.9 Control strategy of the new three-phase inverter

为了使得逆变器在交流负载波动时，三相逆变器仍能够恒压、恒频输出，此处采用闭环控制策略（如图9b 所示）。首先，将给定的频率参考值fref进行积分，得到相位角θ；然后，将给定电压幅值U乘以sinθ，得到最终的参考电压Uref，等式表示为

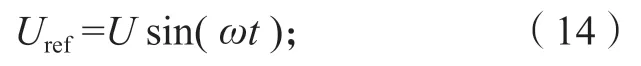
最后，直接将输出侧交流电压Uoa反馈到控制器，形成闭环控制，参考电压Uref与输出电压Uoa进行比较，将误差信号送入准PR 控制器，使得PR 控制器对误差信号进行无静差跟踪。由式（2）可知，为了使Buck 变换器输出电压成直流脉动规律变化，PR 控制器输出信号Uk需要进行绝对值运算和归一化处理后，才能送入PWM 发生器中，与三角波进行脉冲宽度调制。则A 相调制信号为

经过PWM 调制过后，得到Buck 变换器高频开关ST1的控制信号。H 桥是实现Buck 变换器输出端的直流脉动电压波以50 Hz 同步翻转的功能。所以每一相H 桥的4 个开关的控制信号产生方法如图9b 所示。分别以50 Hz 的参考电压Uref与0 做比较，当参考电压大于0 时，Q11、Q14开关导通，Q12、Q13开关关断，输出电压为正弦电压的正半周波形。当参考电压小于0 时，Q12、Q13开通，Q11、Q14关断，输出电压为正弦电压的负半周波形。

4 仿真分析

在Matlab/Simulink 中搭建新型开关模式三相逆变器的仿真模型，仿真参数设置如下（以A 相为例）：直流电源电压为311 V，逆变输出为50 Hz 的交流相电压有效值为220 V，线电压有效值为380 V；星形负载电阻为20 Ω，Buck 电路电感为6 mH，电容为10 μF，开关频率为10 kHz；准PR 控制器的参数设置为ωc=3、kp=1.5、kr=100。

4.1 恒压恒频运行

4.1.1 正常工况

图10 为正常工况下三相逆变器的A 相电压和电流波形图。

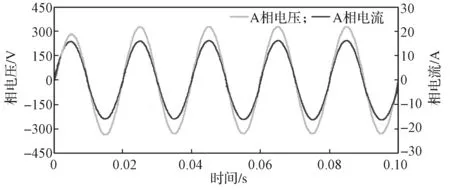
图10 逆变器A 相电压和电流波形图Fig.10 A-phase voltage and current of the inverter

由图10 可以看出，逆变器的输出电压为标准的50 Hz 的交流电压，在0.01 s 后输出电压峰值稳定在311 V，从而实现了恒压恒频控制。

4.1.2 负荷突变

为了验证负荷突变时，逆变器仍然能够实现恒压恒频输出，仿真验证中设置在0.206 s 时负荷突然增大1 倍。其输出相电压和相电流的动态过程如图11所示。

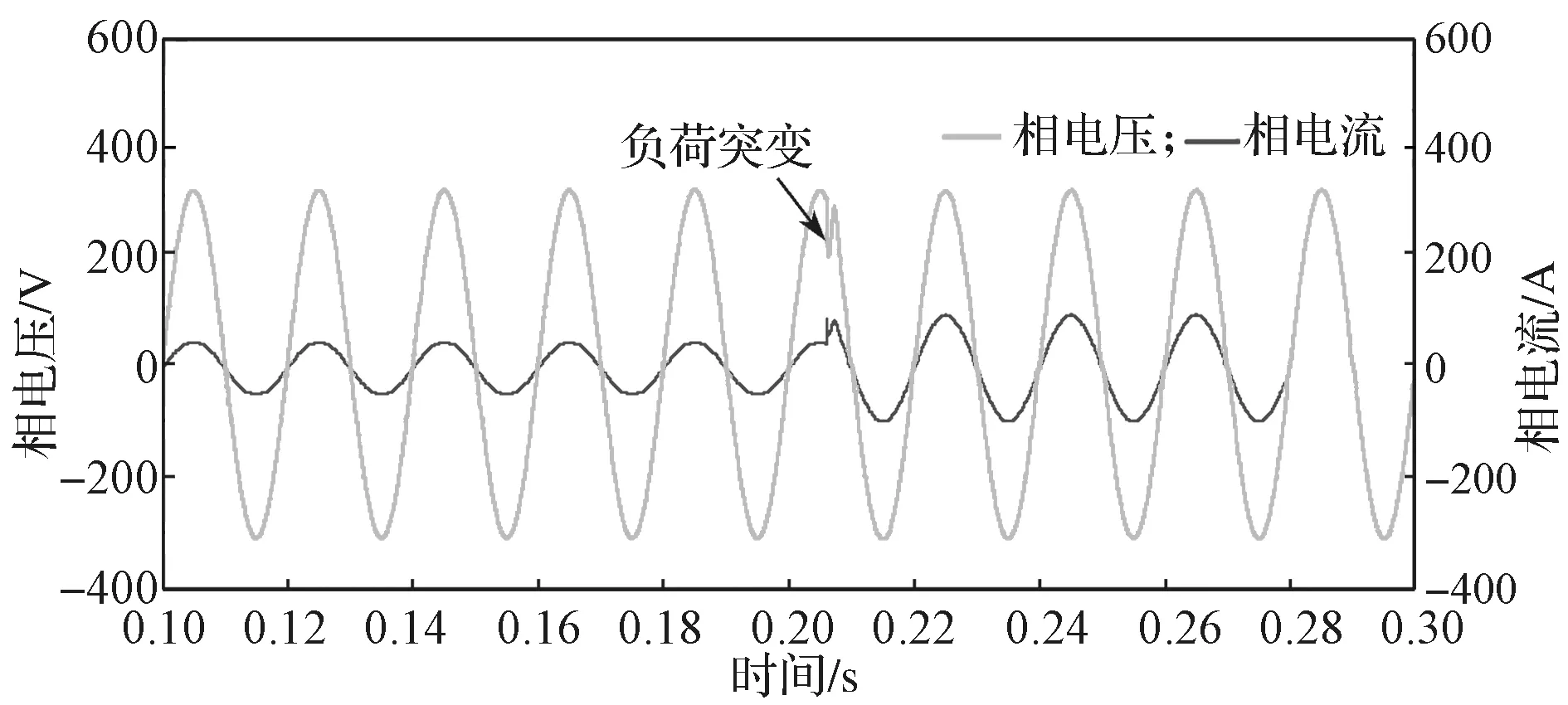
图11 负荷突变时相电压和相电流波形图Fig.11 Waveform of phase voltage and phase current under the condition of a sudden load change

由图11 所示负荷突变时新型三相桥式逆变器输出的电压电流动态波形可以看出，在0.206 s 负荷突然增大1 倍时，输出相电流峰值由15.5 A 增大到31.0 A，因此输出功率也增大了1 倍。在负荷突增1倍时，逆变器输出的三相相电压在0.206 s 时有所波动，从峰值311 V 突变到峰值330 V，但是0.21 s 后就恢复为峰值311 V 的50 Hz 交流稳态输出，从而实现了在负荷突变时的恒压恒频稳态输出。

4.2 直流电压利用率比较

图12 所示为不同模式下三相逆变器的输出三相电压波形。

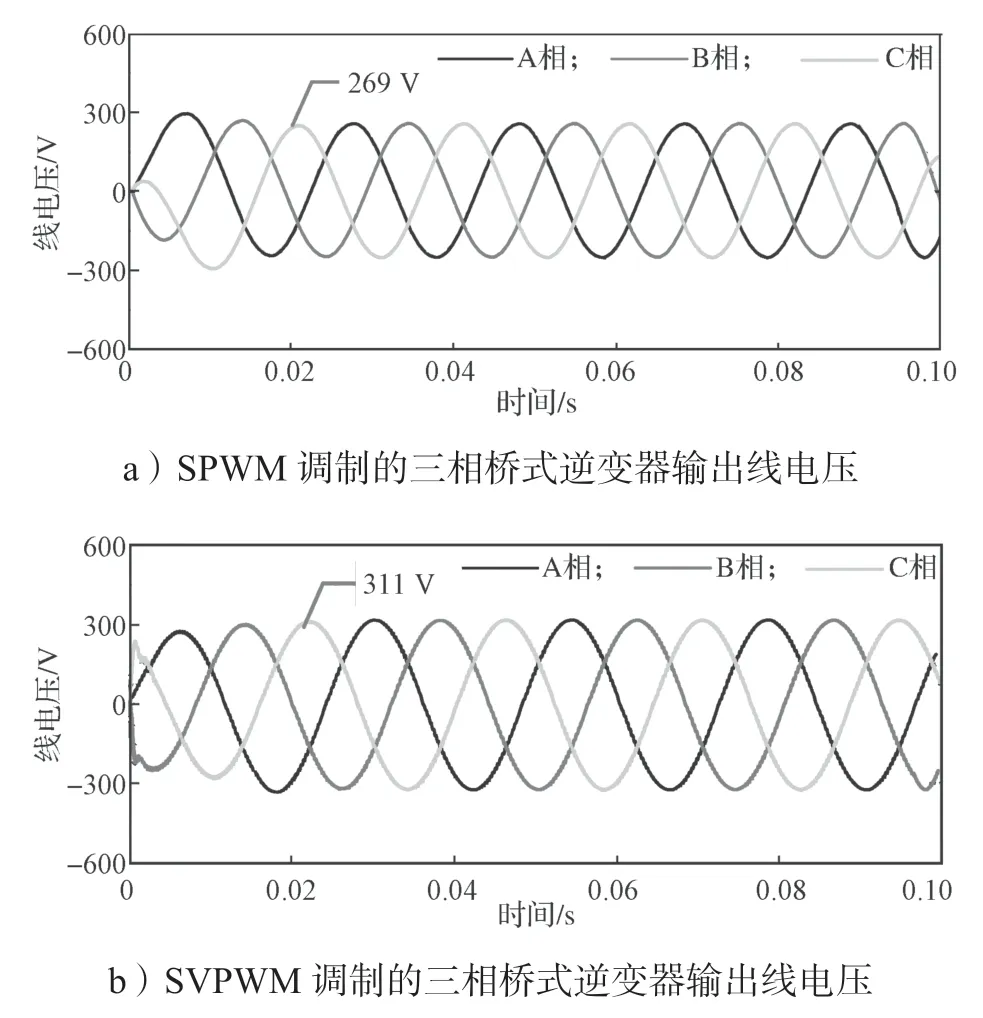
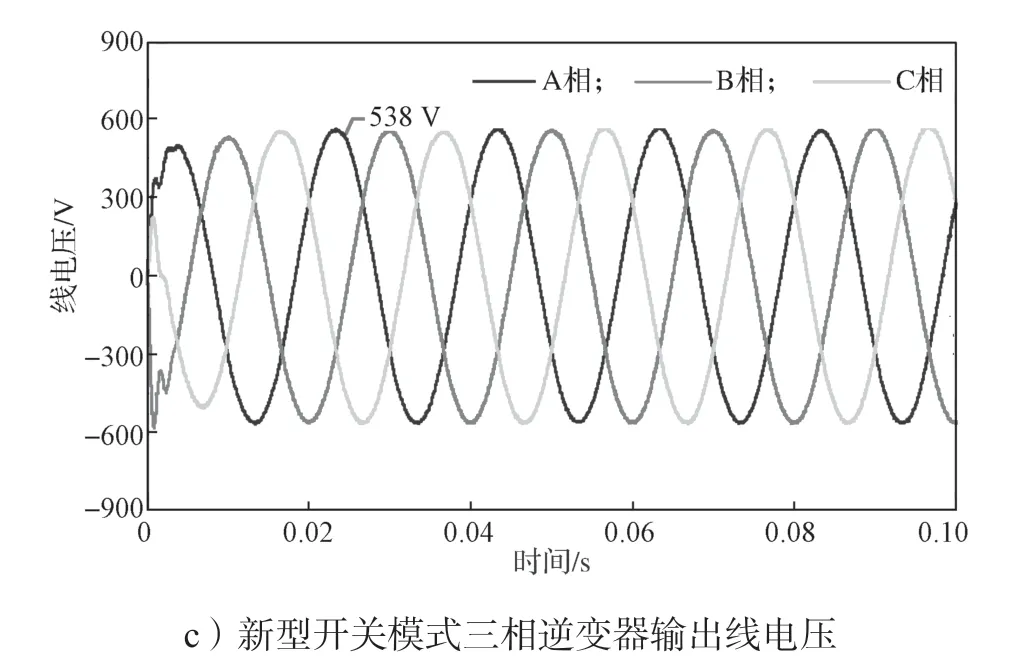
图12 不同模式的逆变器输出三相电压波形图Fig.12 Three phase voltage output from inverter in different modes

为便于比较，将不同开关模式三相逆变器输出线电压绘制成如图13 所示的柱状图。

从图12 和13 中可以看出，新型开关模式三相逆变器的输出线电压峰值约为538 V，然而在直流电源为311 V条件下，传统三相逆变器采用SPWM调制时，输出线电压最大峰值为

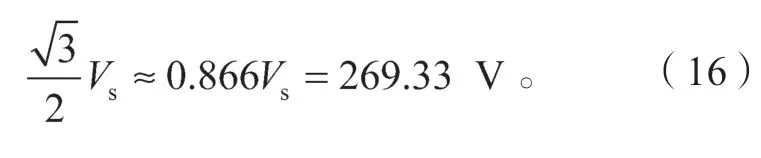
即使采用SVPWM 调制法或者采用三次谐波注入法，三相逆变器的输出线电压的最大值峰值也只有311 V。因此，此新型开关模式三相逆变器直流电压利用率提高为传统三相逆变器采用SPWM 调制时的2 倍；直流电压利用率提高至采用SVPWM 调制时的1.73 倍。

4.3 谐波畸变率比较

在相同的输出滤波电感和电容时，传统三相桥式逆变器和新型三相逆变器的输出电流谐波含量对比如图14 所示。

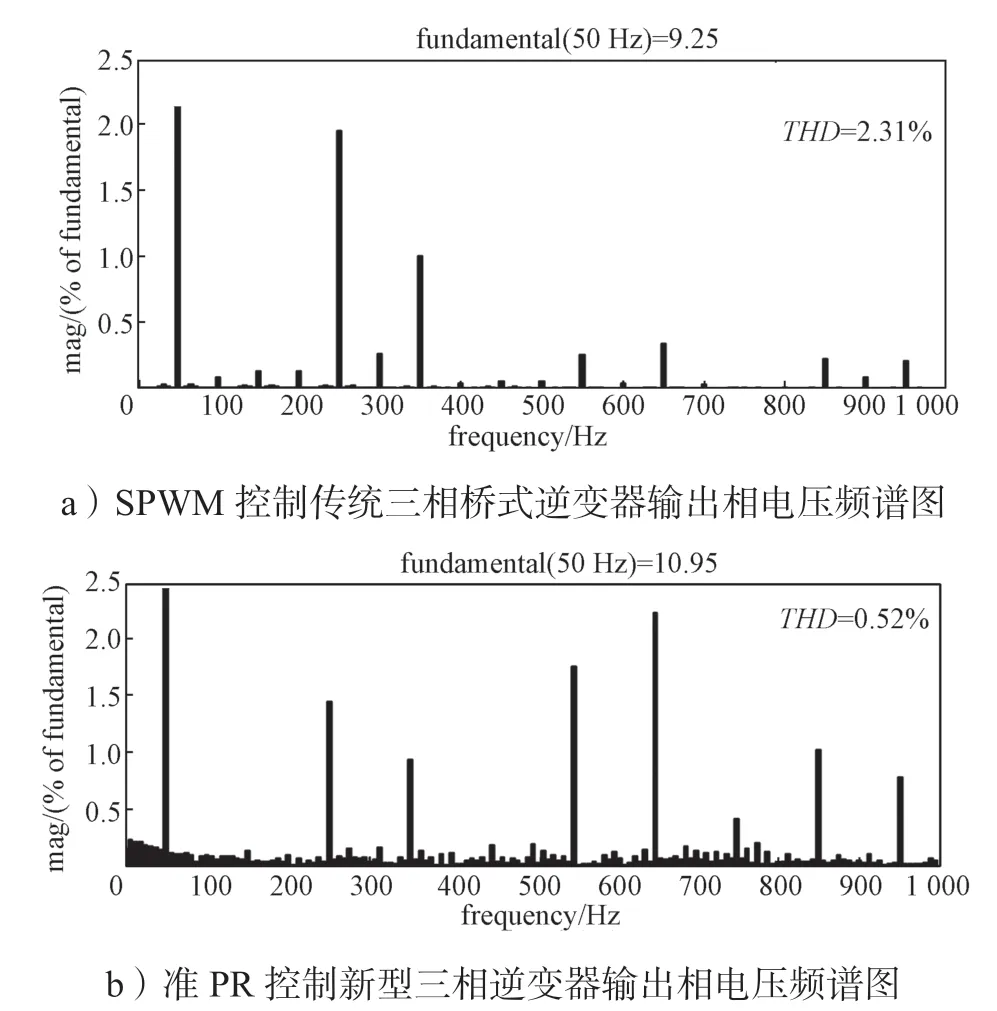
图14 逆变器输出电流谐波含量对比Fig.14 Comparison of harmonic content of the inverter output voltage

从图14a 可以看出，常规三相桥式逆变器输出电流总的谐波畸变率（total harmonic distortion，THD）为2.31%，然而本文所提出的新型三相逆变器的输出电流总谐波畸变率仅为0.52%，最大单次谐波含量低于0.3%。这一结果表明，相比于传统桥式三相逆变器，该新型三相逆变器能显著减少谐波含量，这与前面工作原理分析中所得结论相一致。