基于神经网络的四足机器人SLIP模型运动控制

吴陈成，李 光，谢楚政，于权伟，章晓峰

1 研究背景

移动机器人是自动执行工作的机械装置，其移动范围远大于自身结构的特征尺寸。它既可以接受人类指挥，又可以运行预先编排的程序，甚至可以根据以人工智能技术制定的原则纲领行动。它的任务是协助或取代人类工作，例如在制造业、建筑建造业或其他有危险作业的工作。狭义上的分类包括：轮式移动机器人、足式移动机器人以及轮足混合式移动机器人。相关研究领域有三维环境构建、定位、路径规划、运动控制等。轮式移动机器人在作业过程中对地形要求较高，无法适应复杂的地形。而基于四足哺乳动物的形态设计的四足机器人由于其结构上的特点，能够适应错综复杂的地形且具有较强的运动属性[1-2]。美国波士顿动力公司研发的Big Dog 四足机器人采用液压驱动，具有良好的承载能力，在其控制中也用到SLIP 模型，Big Dog 在近代四足机器人的发展史上具有里程碑意义[3]。波士顿动力公司后续又发布了LS3[4]、Spot、 SpotMini 等一系列先进的四足机器人[5]。瑞士苏黎世联邦理工学院研制的ANYmal[6]和麻省理工学院研制的Cheetah 3[7]灵活性较高。国内宇树科技研发的莱卡狗（Laikago）[8]具有优异的动态性能，其中Unitree A1 款机器狗具有深度视觉功能，可以实现实时3D 地图创建及导航规划。

与传统的固定式机器人不同，四足机器人通过腿部与地面的接触产生相互作用力实现对速度与姿态的控制。而对于四足机器人来说运动的控制十分重要，所以科研工作者们对四足机器人运动过程中的跳跃控制问题进行了研究。为获得良好的运动控制性能，需对四足机器人进行精确建模[9]，但由于现有的四足机器人结构较复杂，又有各种不同的运动步态，所以研究者很难对整个四足机器人系统进行运动学和动力学分析。因此，有必要建立一个简单有效的等效模型以简化四足机器人的运动过程，从而建立一个能够实现对四足机器人有效控制的模型。

R.Blickhan[10]于1989年首先提出了一种弹簧负载倒立摆（spring-loaded inverted pendulum，SLIP）模型，用于简化四足机器人系统，描述四足机器人的运动过程。通过合理设置SLIP 模型的物理参数和初始条件，此模型就能够用来模拟四足机器人的运动过程。SLIP 模型的动力学运动规律实验能够与各种四足哺乳动物的运动实验结果吻合，由于该模型对四足机器人系统进行了简化，所以很大程度上简化了四足机器人控制问题的复杂程度[11-13]。

控制器的结构分为上层运动规划（high-level motion planning）和下层跟随（low-level tracking）。上层运动规划一般基于简化的动力学模型来预测重心和脚的轨迹，而下层跟随则考虑更加复杂的模型来规划各个关节的位置或者力矩。上层运动轨迹的产生一般都要基于模型对未来进行预测，这也就是模型预测控制（model predictive control，MPC）的基本思路。用简化模型的原因是复杂模型的计算量过于庞大，而目前没有较好的方法对其进行实时计算。虽然上层轨迹是基于简化模型的情况，但是下层考虑了更复杂的模型，因此最终产生的关节轨迹符合实际机器人的动力学特性，而且能较好地跟随上层轨迹。

在研究SLIP 模型的运动控制问题时，有些学者通过建立SLIP 模型的动力学方程研究它的运动特性。然而，由于系统的动力学方程是一组非线性方程组，无法得到其具体的解析解，而通过数值分析获得近似解析解的方法需通过大量的迭代运算，不适合实时控制[14]。而在四足机器人跳跃运动过程中，接触地面时会产生碰撞，且系统本身存在阻尼，这会造成能量损失，如何精确计算这部分损失能量也尚待解决。

本文以宇树科技研发的Unitree A1 四足机器人为研究对象，采用弹簧负载倒立摆模型对四足机器人结构进行简化处理，将模型的运动过程分为着陆相与腾空相，并建立了相应的动力学方程。在仿真平台进行动力学仿真时考虑了模型与地面接触时产生的碰撞与阻尼，并利用动力学仿真得到的样本数据训练了一个神经网络。经实验验证，基于神经网络的方法可以较精确地实现对SLIP 模型运动的控制。

2 四足机器人等效SLIP 模型

2.1 SLIP 模型介绍

SLIP 模型是一种简化的描述机器人在运动时状态的模型，包含顶部的质量球与相连的弹簧腿两部分，即用一条弹簧腿等效机器人的腿部，将机器人的机体等效为弹簧腿顶部的一个密度较高的质量球，并忽略机器人腿部质量[15]。SLIP 模型如图1 所示，模型与地面接触点为O点，水平方向为x轴，竖直方向为y轴，重力加速度为g，沿y轴负方向，质量球质心与接触点O水平距离和垂直距离分别为x、y，模型与y轴正方向所成角度为θ，弹簧原长为r0。

2.2 四足机器人到SLIP 模型的简化过程

四足机器人由机体和支撑机体的四条机械腿组成，通过电机驱动机械腿实现机器人站立、行走、奔跑、跳跃等动作，如图2 所示。而SLIP 模型用一个弹簧腿来等效机器人的腿部，将机器人的机体等效为弹簧腿顶部的一个质量球，并忽略机器人腿部质量，其中将四足机器人的四条腿等效为一条腿。

M.H.Raibert 等[16]于1986年提出了“单脚步态（one-foot gaits）”，可将SLIP 模型应用到双足机器人上，只需要满足两个条件，即每次只能由一条腿提供支撑，且着陆相和腾空相交替进行。双足机器人的步态如果满足单脚步态就可将每一步都等效为单腿的SLIP 模型，这个过渡过程很直观。但想要将SLIP模型应用到四足机器人上，就要引入虚拟腿（virtual leg）的概念。多足的过渡基于双足的单脚步态，将四足机器人的四条腿两两分组，每一成对的组作为一个控制单元，则实际可等效为一个单腿模型，这就是虚拟腿的含义。

使多足机器人遵循单脚步态，那么多足机器人的控制就可以等效为双足机器人的控制，进而转化到单腿模式。目前，四足机器人的步态主要有对角小跑（Trot）、踱步步态（Pace）、跳跃步态（Bound）。对角小跑指每次迈步同时抬起对角线上的两条腿，并以二分之一的相位差轮流向前迈步；踱步步态指每次迈步时会同时抬起身体同侧的两条腿，身体异侧的两对腿则以二分之一的相位差轮流向前迈步；跳跃步态指每次迈步同时抬起身体前后同侧的两条腿，以二分之一的相位差轮流向前迈步。在四足机器人不同步态下，可以将相同运动特征的两个腿组队看成是一条腿，形成不同的等效虚拟腿。各种步态的等效虚拟腿如图3 所示。

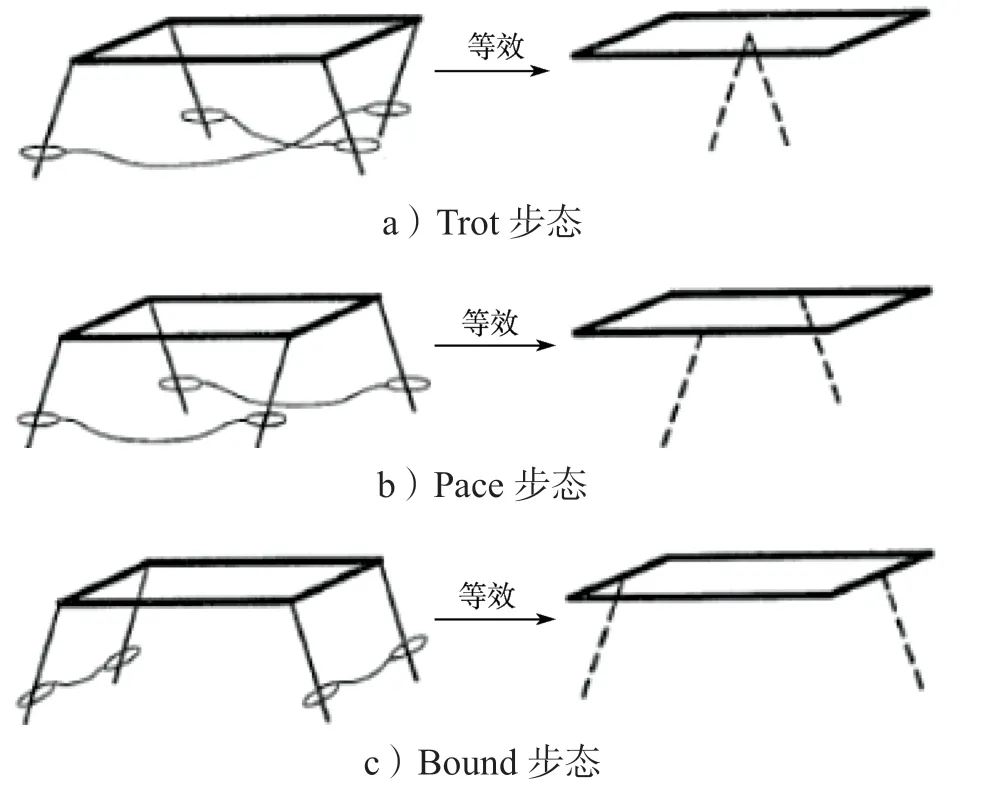
图3 不同步态下的等效虚拟腿Fig.3 Equivalent virtual legs in different gaits

由图3c 可知，由此实现了四足机器人在跳跃步态下到SLIP 模型的简化。将复杂的四足机器人系统简化为更加易于控制和研究的单腿SLIP 模型，其简化过程如图4 所示。

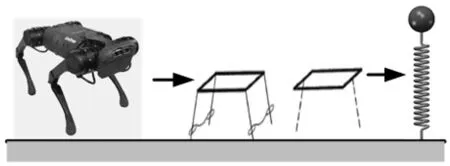
图4 四足机器人模型简化过程Fig.4 Simplified quadruped robot model

2.3 SLIP 模型运动过程分析

尽管四足哺乳动物有各种各样的步态和运动形式，但根据仿生学的研究内容可知，其步态周期基本处于“伸长—触地—发力—离地—缩短”运动循环。四足动物利用下肢独特的生物结构，在运动过程中尽量减小着陆时的冲击，并储存能量以供重复使用。四足动物的这些运动特性在SLIP 模型上也有相应体现。例如当模型的弹簧腿与地面碰撞时，可以减小冲击，能量可转化为弹簧的弹性势能并存储。

将四足机器人的运动简化为SLIP 模型后，其一个完整的步态周期包括4部分：“腾空—着陆—回弹—腾空”，如图5 所示。

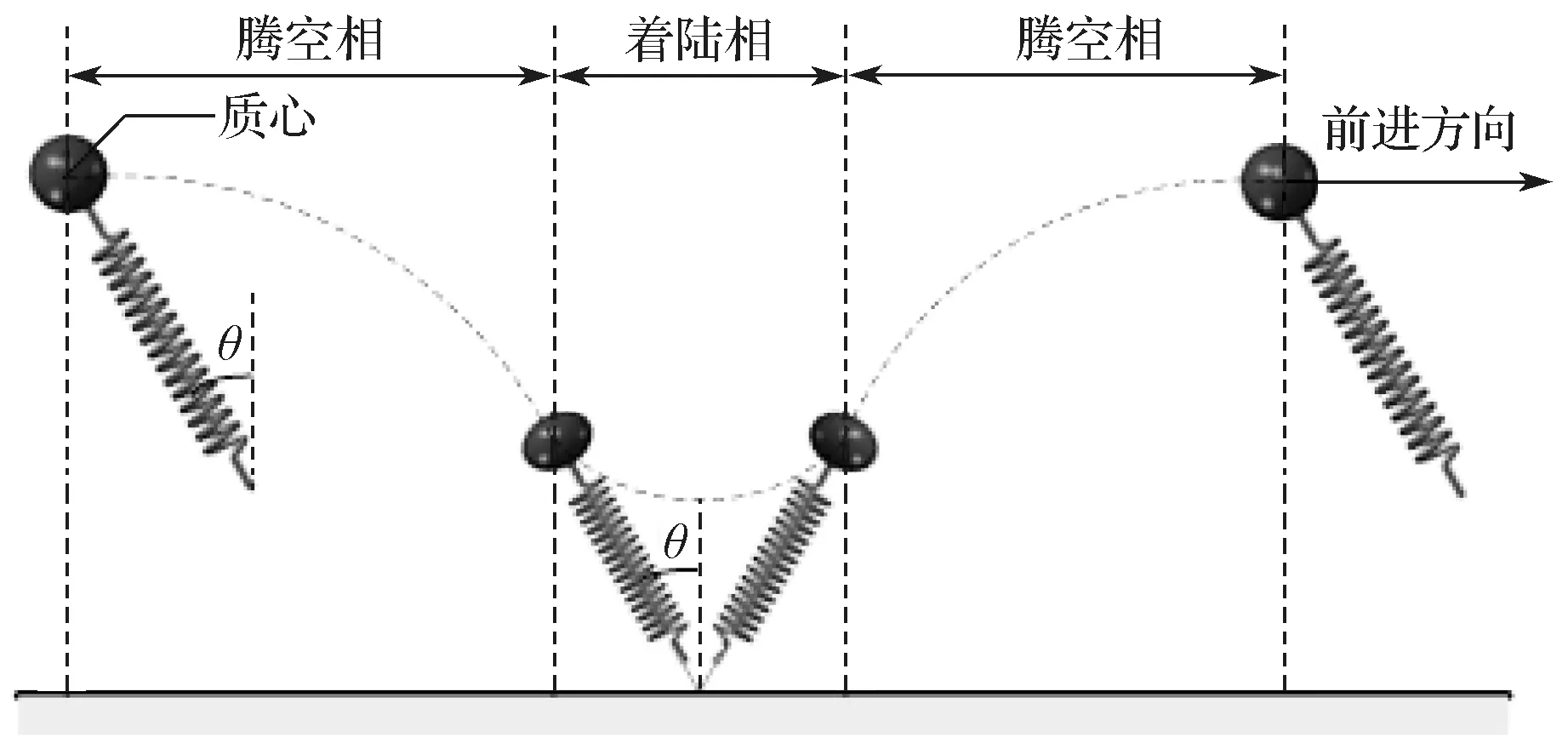
图5 SLIP 模型一个运动周期示意图Fig.5 Schematic diagram of the motion cycle of SLIP model

由图5 可知，一个运动周期的各状态如下：

1）腾空。模型与地面无接触，弹簧长度为原长度，此时模型只受到竖直向下的重力作用。

2）着陆。当模型腿部刚开始接触地面时，弹簧由自然状态开始被压缩，此时模型不仅受到重力作用，还受到地面给予的支撑力与摩擦力作用。模型的动能和重力势能转化为弹簧腿的弹性势能，直至弹簧达到最大压缩量，且模型沿竖直方向的速度为0。

3）回弹。弹簧压缩量达到最大后，弹簧的弹力大于机体所受重力沿弹簧的分力，使得机体有一个向上的加速度，于是机体开始向上运动，弹簧在之前储存的弹性势能继而又转化为机体的动能和重力势能，直至弹簧长度恢复原长，模型即将脱离地面。

4）腾空。由于惯性作用，模型会继续向上运动并脱离地面，此时弹簧长度已经恢复原长，弹力为0，模型又只受到竖直向下的重力作用，直至机体质心上升到最高点，模型竖直方向上的速度减为0，完成一个运动周期。

由腾空相到着陆相的转换条件就是弹簧处于原长且即将被压缩，而相反的转换条件就是弹簧被压缩且即将恢复到原长。

SLIP 模型机体的质量为m，等效弹簧腿的长度为r0，且忽略其质量，而等效弹簧腿的刚度为k，阻尼为c。SLIP 模型与竖直方向的夹角为θ，可用来描述模型在平面内的姿态。

当模型处于腾空相时，弹簧长度为原长，弹力为0，模型只受到沿竖直向下的重力作用，机体质心的运动轨迹为一条抛物线，可以很容易地得到腾空相时系统的动力学方程，为

g为重力加速度。

当模型处于着陆相时，其运动分析比腾空相复杂。弹簧腿末端与地面接触时机体、腿部弹簧和地面形成了一个力学模型。此时系统总的动能为

式中：EK为系统总动能；

平动动能的计算公式为

式中： 为弹簧长度变化速率；

r为弹簧腿长度；

着陆相的系统势能包括重力势能和等效弹簧的弹性势能，计算式如下：

由式（3）和式（4）可求得系统的拉格朗日函数如下：

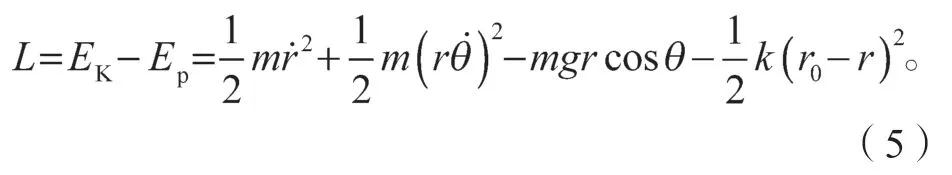
定义广义坐标系q=（r,θ），则系统着陆相的动力学方程为

为了简化系统，在其着陆相时只考虑弹簧阻尼力-c，则系统着陆相动力学方程可进一步表示为

将拉格朗日函数代入式（7）的推导结果如下：

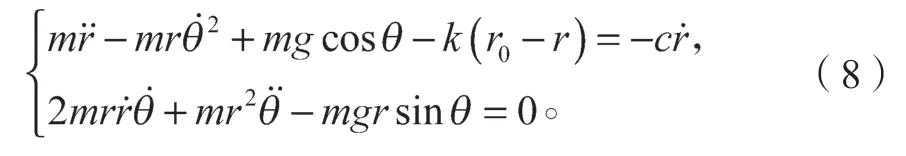
3 仿真实验与样本获取

3.1 仿真环境的建立

在机械系统动力学自动分析（automatic dynamic analysis of mechanical systems，ADAMS）软件中建立四足机器人的简化模型，即SLIP 动力学模型，如图6 所示。

图6 SLIP 动力学模型Fig.6 SLIP dynamics model

在图6 中，将机器人的机体等效为弹簧腿顶部的一个质量球，其质量参考Unitree A1 四足机器人，取值为12 kg，球半径为5 cm；弹簧腿为长度是40 cm的弹簧阻尼器，没有质量；弹簧腿下方末端处的实心球，用来模拟四足机器人足部，半径为2.5 cm，由于SLIP 模型忽略腿部质量特性，而仿真时质量不能为0，所以将其质量设置为0.000 1 kg，以忽略其影响。

腿部等效弹簧的刚度计算参考生物力学的研究成果，表示为机体质量的函数[17]，如式（9）：

等效弹簧的阻尼与运动质点的速度大小成正比，取其值为0.014[18]。由此可以得到四足机器人SLIP动力学模型的各项参数，如表1 所示。

表1 四足机器人SLIP 动力学模型参数Table 1 Parameters of SLIP dynamics model of quadruped robots

上述SLIP 系统具有足部与机体之间的轴向伸缩自由度，在模型足部位置处添加足部与机体质量球之间的滑动副，可以约束弹簧腿只沿弹簧轴伸缩运动。

为了更加真实地模拟SLIP 系统在跳跃时与地面的接触过程，需要设置地面参数以及模型与地面间的接触力和摩擦系数，将地面的碰撞刚度设置为1×108，模型与地面间的接触力类型为库仑摩擦，静摩擦系数为0.5，动摩擦系数为0.4。

3.2 样本数据的获取

模型初始位置顶部质量球质心距离地面的高度为70 cm，模拟SLIP 模型在不同水平初速度v0下，以不同的着陆角触地，记录顶部质量球质心弹起达到最高点时的水平末速度v1和质心高度h，其中一些记录数据如表2 所示。

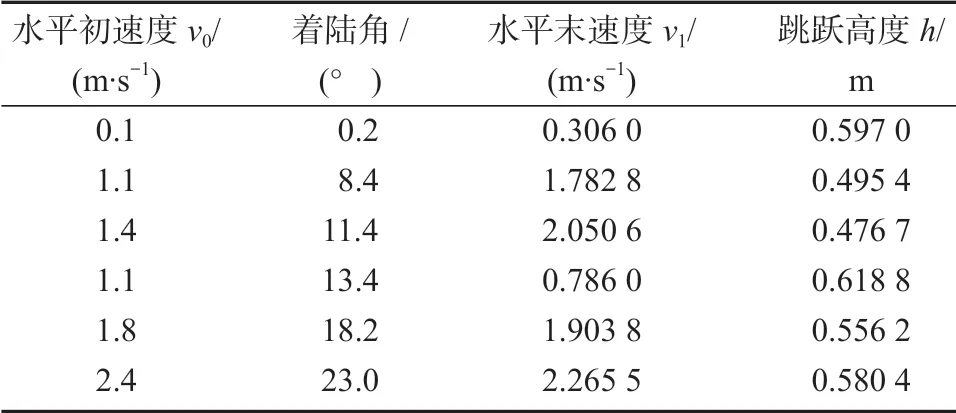
表2 SLIP 模型仿真数据Table 2 SLIP model simulation data

经由不断地仿真，最终得到了一份包含817 份样本的数据。

4 BP 神经网络的构建及训练

构建3 层前向BP（back propagation）神经网络，第一层为输入神经元，共3 个，分别为水平初速度v0、水平末速度v1和质心弹跳高度h；第二层为隐藏层神经元，共6 个；第三层为输出神经元，输出为着陆角θ。各层之间的传递函数选择正切S型传递函数（tansig），学习率设置为0.05。将之前得到的817份样本数据输入到Matlab 中，利用randperm 函数将817 份数据随机打乱，并选取前800 份作为训练样本，后17 份作为测试样本。通过多次尝试，发现当训练的迭代次数为44 次时，训练效果最好，3 条Mean Squared Error(均方误差)曲线拟合效果较好，用于训练和测试的样本数据拟合效果也较好，神经网络的均方误差迭代44 次时为1.5×10-2，输出的是着陆角的均方误差，如图7 所示。

图7 神经网络均方误差曲线Fig.7 Neural network mean square error graph

用于训练的样本数据拟合度达到0.999 79，用于测试的样本数据拟合度达到0.999 87，理想的状态下拟合度达到1 时最好。从图8 中可看出所有样本点基本上都处于一条直线上。

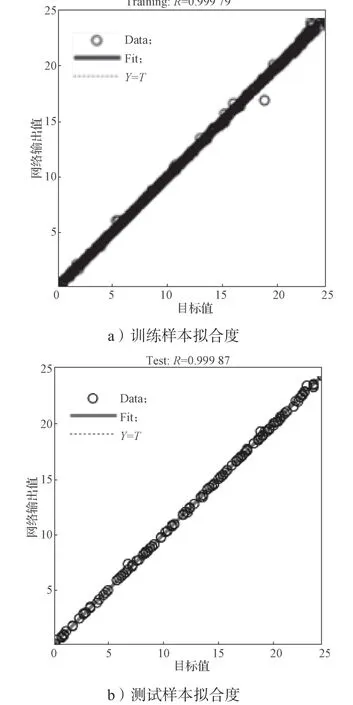
图8 样本数据拟合度Fig.8 Fitting degree of sample data

5 实验验证

为测试训练好的神经网络，取5 个不存在于数据样本中的未知样本，样本输入包括3 个参数：水平初速度v0、期望水平末速度vld和期望质心弹跳高度hd，样本输出为神经网络计算出的着陆角θ。然后利用在ADAMS 中建立的SLIP 动力学模型进行仿真验证，仿真结果如图9 所示。

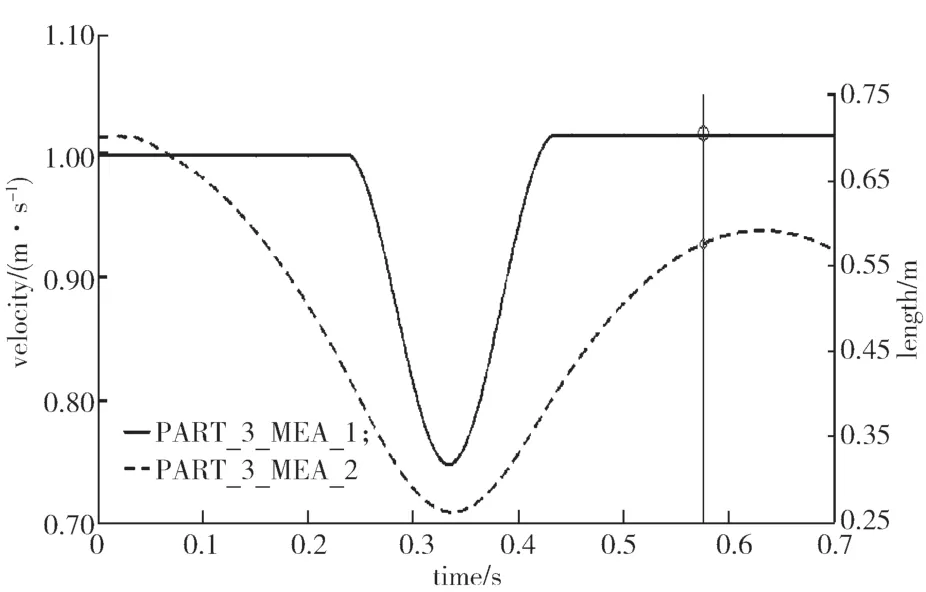
图9 ADAMS 仿真验证Fig.9 ADAMS simulation verification

在图9 中，实线为SLIP 模型运动时质量球质心的水平速度曲线，虚线则是质心的高度曲线。

将仿真数据代入神经网络计算出着陆角，并以水平初速度v0进行仿真，得到最终的水平末速度v1和质心弹跳高度h。其数据如表3 所示。从表3 中可以得出，v1的最大偏差为0.018 6 m/s，h的最大偏差为0.005 6 m，这个偏差可以接受，故神经网络可以用于SLIP 模型的运动控制。实现对SLIP 模型的加速、减速、匀速、急停以及稳定高度的运动控制。

表3 验证样本及误差Table 3 Sample and error verification

6 结语

本文研究了四足机器人跳跃步态时的运动控制问题。采用SLIP 模型简化了四足机器人的结构，并建立了模型的动力学方程。通过分析着陆角对SLIP模型系统的影响，提出了通过调节着陆角实现对SLIP 模型水平速度和跳跃高度的控制。利用训练好的BP 神经网络对着陆角进行预测，得到期望的水平速度和跳跃高度。ADAMS 仿真结果表明，本方法可以实现对SLIP 模型的运动控制。