汽油辛烷值损失优化方案的数学建模与求解

陆天浩，李玲玲，陈宇峰，汤 琼

0 引言

汽油的辛烷值作为汽油的商品牌号（例如89#、92#、95#），是衡量汽油发动机燃料抗爆性能优劣的重要指标。辛烷值越高，表示其抗爆性能越好，发动机压缩比越高[1]。辛烷值的提高可以提升发动机功率，增加车辆行程；同时还能起到节约燃料，减轻使用者经济负担的作用。对于小型车辆而言，汽油是其主要的燃料，汽油燃烧产生的尾气是影响大气环境的重要因素。辛烷值反映了汽油的燃烧性能，然而当前的脱硫催化裂化汽油技术，使汽油的辛烷值大大降低。因此提高辛烷值是提高经济效益和改善环境的一个重要手段[2]。

为了解决上述问题，针对“华为杯”第十七届中国研究生数学建模竞赛①本文为“华为杯”第十七届中国研究生数学建模竞赛二等奖论文。B 题：汽油辛烷值建模，将BP（back propagation）神经网络模型与遗传算法[3-8]引入预测与优化任务中，并通过预测优化找到符合条件的优化方案。

1 数据处理

1.1 数据预处理

用数学建模竞赛B 题所提供的数据集作为原始数据集。在数据集中，共有325 个样本，根据样本采集时间排序，采集时间为2017-04—2020-05。每个样本包含由原料性质、产品性质、待生吸附剂性质 、再生吸附剂性质等不同操作变量构成的354 个采集位节点。由于是原始数据，不同样本中的不同位节点存在未采集数据或数据缺失等情况。如果不同样本的同一位节点缺失数据较多，则该位节点不能准确反映变化情况，需要删除该位节点。如果不同位节点的同一样本数据较多，同样需要删除该样本。对于缺失值个数较少的位节点，可根据临近时间的样本对应位节点值进行填充。再对筛选后的数据采用3σ准则去除异常值；根据实际应用背景确定取值范围，将超过范围的位节点或对应样本数据剔除。具体数据处理如下。

1）遍历整个数据表，将采集值缺失过多的样本及位节点删除。经过筛选，共删除12 个位节点，具体名称如表1 所示。这类位节点由于信息缺失过多，因此不能清晰体现该位节点对辛烷值损失的影响。

表1 第一步被删除的位节点Table 1 Removed sites in the first step

2）对位节点进行过滤操作，删除数值全部为空值或无法通过相邻样本进行填充的位节点。前者没有数值变化，不能体现该位节点对辛烷值损失的影响。后者只有部分时间段样本，不能完整地体现该位节点对辛烷值损失的作用。过滤后，删除19 个位节点，具体名称如表2 所示。

表2 第二步被删除的位节点Table 2 Removed sites in the second step

3）对于存在少量空缺值的位节点，用相邻样本的均值进行填补，需要补充的位节点如表3 所示。

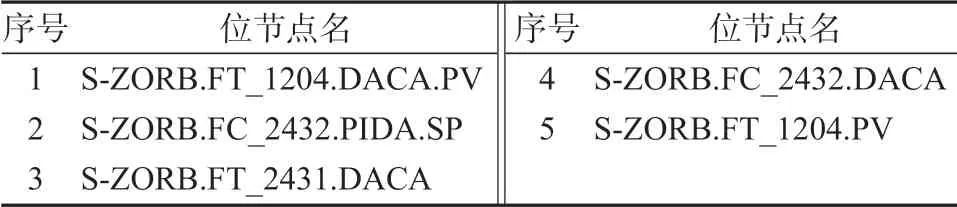
表3 缺省值填补位节点Table 3 Nodes filled by the default value

4）根据不同操作变量实际取值范围，剔除位节点采集值异常的32, 29, 27 号样本。

5）使用3σ准则去除异常值及其所带来的影响。

完成上述预处理后，将285, 313 号样本结果加入到对应位置。

1.2 数据降维

模型1 主成分分析

主成分分析法是使用线性降维的方法来寻找模型的主要操作变量，以达到精简影响因素数量的目的。本文使用SPSS 进行主成分分析，使多维的数据降维得到少数几个综合指标，具体操作步骤如下：

1）数据标准化

设x1,x2,…,xm为m个主成分分析变量，aij为m个评价对象中第i个评价对象对应于第j个分析变量的取值。将每个aij值标准化，

标准化指标变量，即

2）计算数据的相关系数矩阵

相关系数矩阵R的具体表达式为

式中，rpq为第p个指标与第q个指标之间的相关系数，且

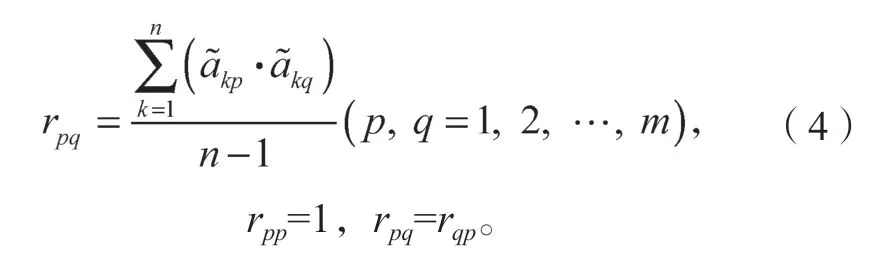
使用主成分分析法对数据集中的320 个位节点进行分析。第一次实验中，将主成分个数设置为25，共筛选出200 多个变量。但由于决定主成分因子的操作变量种类各不相同，在工艺和设备操作上没有很强的关联性。因此将主成分个数设为5，然后重新实验，结果如下：反应过滤器压差，反应器上部温度，SZORB.FT_9001.TOTAL，SZORB.FT_5201.TOTAL，SZORB.FT_9102.TOTAL。第二次实验结果优于第一次，但由于传统方法的关联模型变量少、要求高，因此响应慢、效果差，且5 个主成分因子只能解释59.374%的结果。

总的来说，通过对位节点进行降维，可以得到一部分主要操作变量。但是由于操作变量之间具有高度非线性和相互强耦合的关系，使用主成分分析法筛选出的主要操作变量影响因子较低，不具有很强的解释性，因此本文采用非线性的降维方法。

模型2 层次聚类法

由于数据集中的320 个有效位节点之间具有高度非线性和相互强耦合关系，为了寻找具有代表性和独立性的主要操作变量，再采用非线性的层次聚类法进行筛选。最后将主成分分析与层次聚类法筛选出的结果进行综合分析，得出最终建模需要的主要操作变量。构建过程如下：

参考欧几里德距离评价，在数据不规范时，皮尔逊相关系数会给出更好的结果，故本文使用皮尔逊相关系数来寻找模型的主要操作变量。具体算法见式（5）（6）。

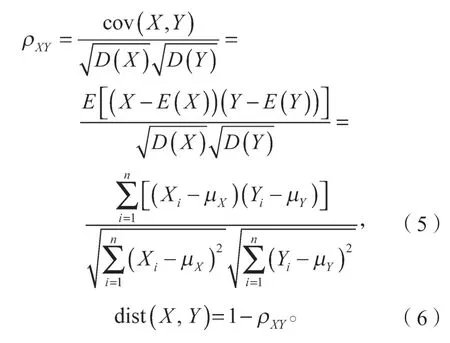
式（5）（6）中：X、Y为两个不同的变量；

μX、μY和D(X)、D(Y)分别为变量X、Y的均值和方差；

ρXY为两变量X、Y间的皮尔逊相关系数，当2个变量完全匹配时，ρXY=1，当2 个变量毫无关系时，ρXY=0。

为了使相似度越大的两个变量之间距离越小，采用1 与皮尔逊相关系数的差值来衡量[9]，见式（6）。

使用SPSS 进行层次聚类分析，再与主成分分析得到的结果综合分析后，得到了13 个主要变量：氢油比、反应过滤器压差、反应器上部温度、反应器底部温度、烯烃含量、芳烃含量、反应器顶低压差、待生吸附剂性质（焦炭含量）、待生吸附剂性质（硫含量）、再生吸附剂性质（焦炭含量）、再生吸附剂性质（硫含量）、辛烷值和硫含量。结合工艺要求和操作经验发现这13 个主要变量符合实际情况，并在后面的辛烷值损失模型建立和优化过程中，可呈现较好的效果，证明了这13 个主要变量具有有效性和代表性。

2 基于BP 神经网络的辛烷值损失预测模型

反向传播网络可以拟合任何非线性函数，是可以实现从输入到输出的端到端网络，而且训练网络的方法非常简单、有效，只需要学习网络参数即可。通过数据预处理与数据降维，将13 个主要变量作为神经网络的输入进行训练。基于BP 神经网络的辛烷值损失预测模型网络结构图如图1 所示[8]。神经网络模型可分为两部分：第一部分神经网络有800 层，作为特征提取层；另一部分为单层全连接层，作为预测层。需要注意的是，在模型选择时，输入输出的维数固定，中间的隐藏层部分需要考虑是否全连接。图中的箭头表示数据流动的方向，即模型的流程；w表示神经网络中的权重矩阵，权重可通过训练得到；B表示各层神经元的偏置，可以使模型具有更鲁棒的表达能力。

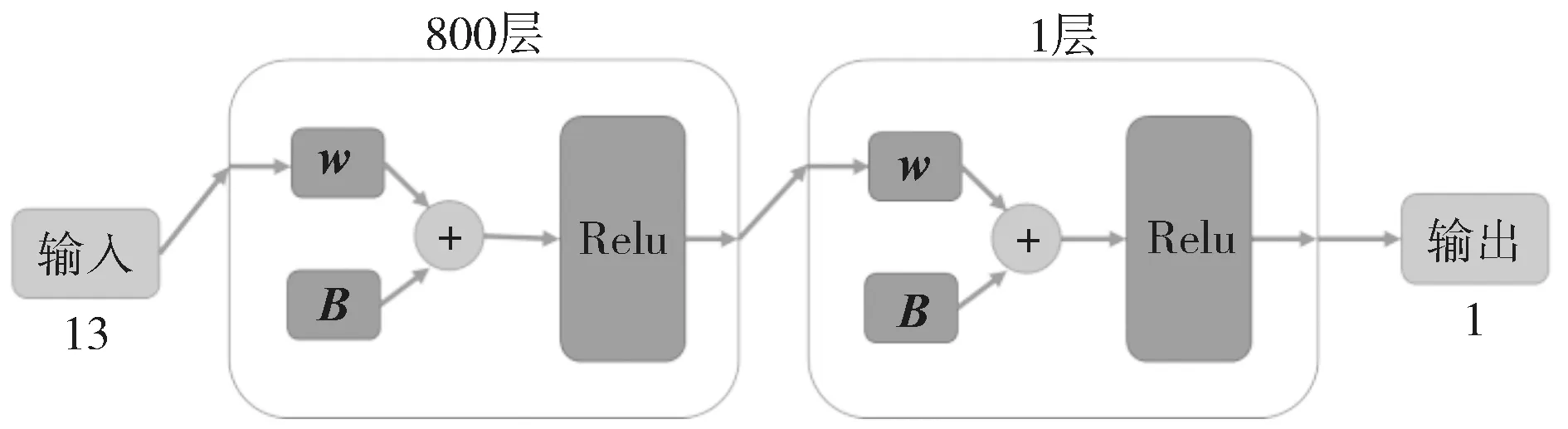
图1 基于BP 神经网络的辛烷值损失预测模型网络结构图Fig.1 Network structure diagram of octane loss prediction model based on BP neural network

模型（反向传播梯度）在更新网络参数时，为避免波动过大出现梯度消失或梯度爆炸现象，导致模型崩溃，需要对输入进行零均值化与归一化，使输入数据的分布统一。经过归一化，输入被约束在[-1, 1]的区间内。

第一步零均值化

式中：xi为某一主要变量的某条样本采样值。

m为主要变量的样本个数。

第二步归一化方差

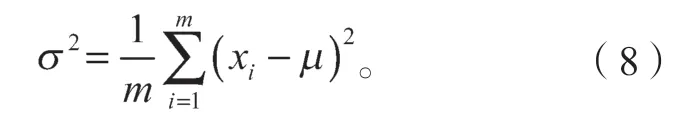
在神经网络中添加激活函数，可以增加网络的非线性表达能力，并解决线性模型不能很好描述的函数

关系[5]。神经网络中所采用Relu 激活函数为

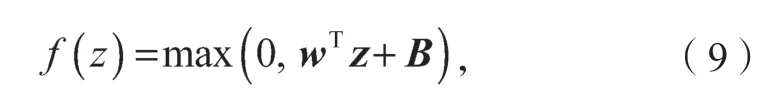
式中：z为激活函数的输入，在本文的网络中为激活函数前一层神经元的输出；

B为对应层神经元的偏置（参见图1）。

Relu 函数在正区间解决了梯度消失的问题，而且使神经网络的收敛速度和计算速度较使用其他激活函数（如sigmoid 等）有明显提高，起到了类似Dropout 的各层神经元随机连接的效果。

考虑到神经网络的输入数据为筛选出的主要操作变量，故采用均方误差（mean square error，MSE）来进行模型的评价。MSE 可以评价数据的变化程度，其值越小说明模型预测结果具有更好的精确度[6]，且具有较小的波动。具体表达式如下：

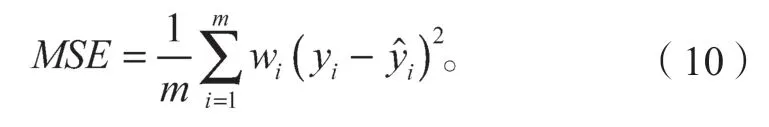
式中：yi、分别为辛烷值损失真实值和模型预测值；wi为神经网络中各预测值的权重。

3 模型求解

在对神经网络模型的实际训练过程中，采用Adam 优化器进行梯度更新。相比于传统的随机梯度下降，Adam 通过计算梯度矩阵为各个参数设置更加灵活的学习速率，对变化频繁的参数采用大步长进行学习，对于稀疏的参数采用小步长进行学习。第k步梯度gk更新如式（11）所示。

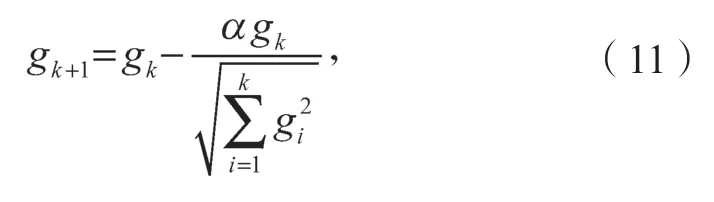
式中α为调节系数，用于调节变化快慢。

将整个数据集划分为80%的训练集和20%的测试集。测试集不参与模型训练，在测试集上通过模型的预测结果来观察模型的实际泛化能力。经过2 048 Epochs 训练，模型的损失函数变化如图2 所示。

由图2 可知，随着训练次数的增加，在测试集上的损失值逐渐降低，在2 000 次左右达到了9.928×10-6，这说明模型有良好的泛化性能。

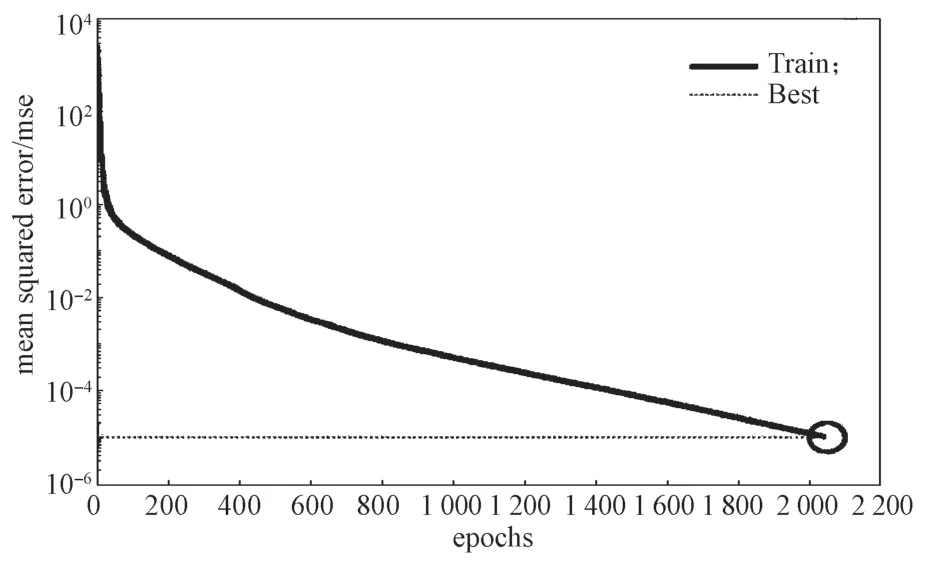
图2 损失函数的变化图Fig.2 Change diagram of the loss function

以损失函数的变化作为本研究中神经网络预测模型的测试标准之一。使用Matlab 软件建立网络的训练参数如下：迭代次数为2 048，学习率为0.01。训练时模型参数的变化如图3所示。由图3a可以看出，随着epoch 的增加，模型梯度逐渐减小，变化趋势逐渐稳定。图3b 可以看出在训练时没有出现模型崩溃现象，具有很好的稳定性。

图3 训练时神经网络模型参数变化图Fig.3 Neural network model parameter variation diagram during training

经过训练，训练模型的最终回归结果如图4 所示。由图4 可以看出，目标值和输出结果基本上在直线y=x附近分布，说明训练结果比较理想。

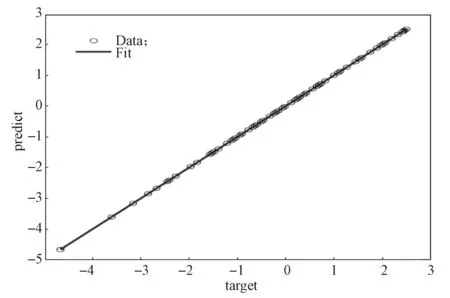
图4 模型的回归结果Fig.4 Regression results of the model

图5 为各样本的辛烷值损失实际值与预测值的分布情况。由图5 可以看出，模型拟合效果明显，可以较好地表达辛烷值的变化情况，并且能取得很好的预测效果。

图5 各样本预测值与真实值分布图Fig.5 Predicted value and true value distribution ofeach individual sample

图6 为3 509 次迭代的损失函数变化图。由图可以看出，在训练2 000 次以后，损失函数下降趋势基本趋于稳定，与图2 中2 048 次迭代的结果相比，MSE在预测和训练上的变化区别不大，拟合程度较高，这说明模型具有良好的有效性和泛化能力。

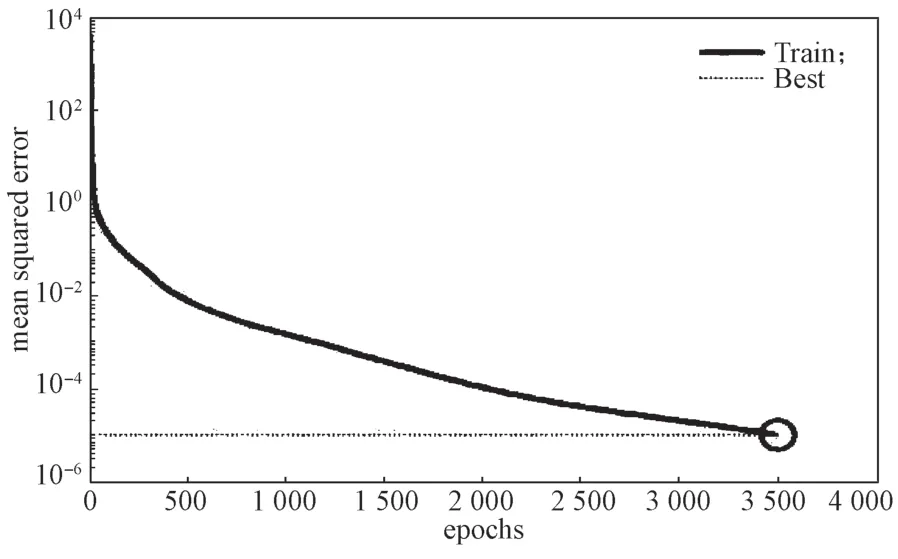
图6 3 509 次迭代损失函数变化图Fig.6 Loss function variation diagram for 3 509 iterations

4 基于遗传算法的方案优化

遗传算法是一种随机化搜索方法，是一种模拟达尔文进化论和孟德尔遗传学机理的计算模型。遗传算法由编码、适应度评估和遗传运算3 部分组成[7]。根据损失散点图，将损失变化通过三角函数进行拟合，即可得到每一个样本的损失值。由于每一个样本包含13 个主要操作变量，损失值可以由操作变量表达，在此可将问题转变为基于主要操作变量的曲线优化问题。利用遗传算法解决多元非线性回归问题，并向最小化损失值的方向优化，得到13 个主要操作变量的对应取值。根据变量的取值范围，得到对应主要变量的优化操作条件。

对于本问题，使用传统方法难以获得最优解，而多峰最优化问题具有多个局部解的特性，因此使用多峰非线性方法来求解，具体实验参数设置如表4 所示。其中，自变量上下界用来表示每个主要操作变量取值范围，交叉概率、变异概率用于控制个体改变频率，设置迭代次数为1 000，使算法能够得到足够稳定的优化解。

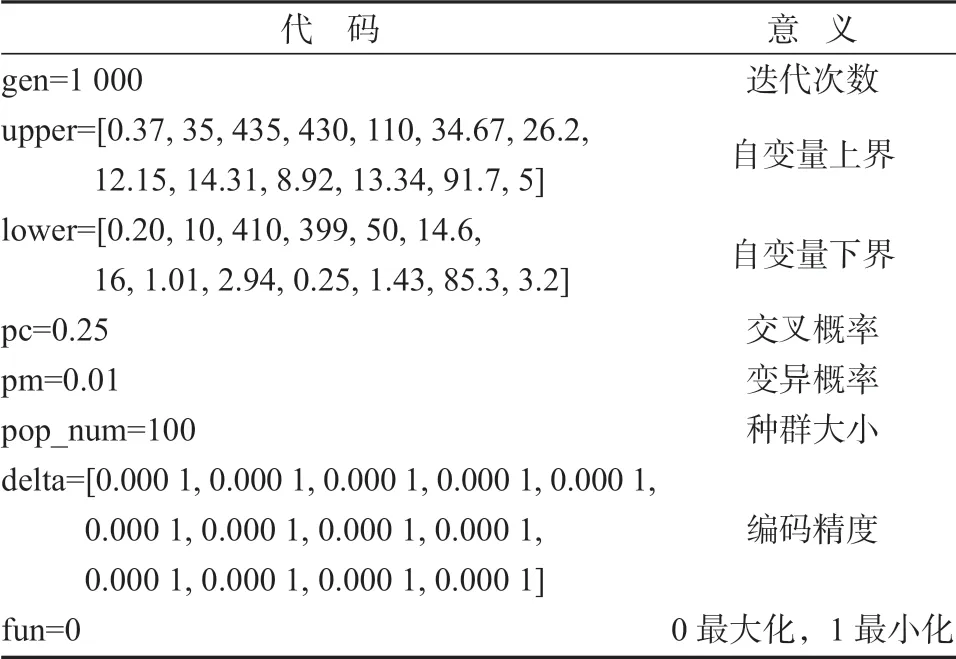
表4 实验参数设置Table 4 Experimental parameter setting

经过实验，遗传算法的损失变化如图7 所示。由图7 可以看出，随着迭代次数增加，损失的波动幅度逐渐减小，最终解逐渐趋于稳定。损失变化曲线表达式为

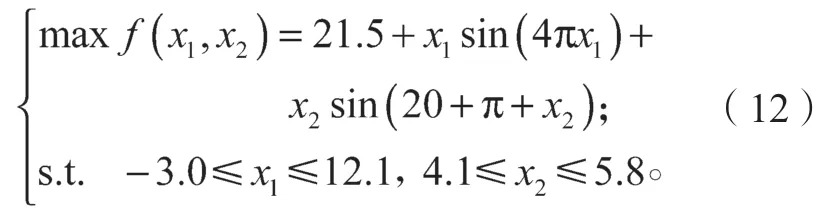
图7 遗传算法的损失变化曲线Fig.7 Loss change curve of genetic algorithm

遗传算法最优个体得分曲线如图8 所示。由图8可能看出，遗传算法在400 次迭代后每代最优函数值变化逐渐稳定，这证明算法已逐渐收敛于最优解。

图8 每代最优个体得分变化曲线Fig.8 Optimal individual score variation for each generation

通过上述遗传算法，可以得到一批子代，每个子代对应一组变量。根据辛烷值损失值与13 个变量之间的关系，建立如下损失值与主要变量间的表达式：

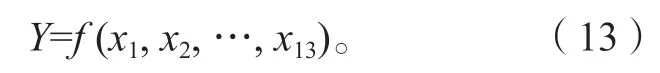
由于优化问题一般是从凸函数最小化寻找最优解，因此采取最小化f值的方式，获得x变量的取值，x对应13个主要操作变量。经过遗传算法的编码解码，从遗传算法中选择降幅大于30%的样本，每个样本对应主要变量优化后的一种操作条件。符合条件的优化方案，按照降幅比降序排列后，结果如表5 所示。当13 个主要变量分别优化至表5 首行对应数值时，所能达到的降幅比为44.822%，是所有得到的优化方案中的最优解。

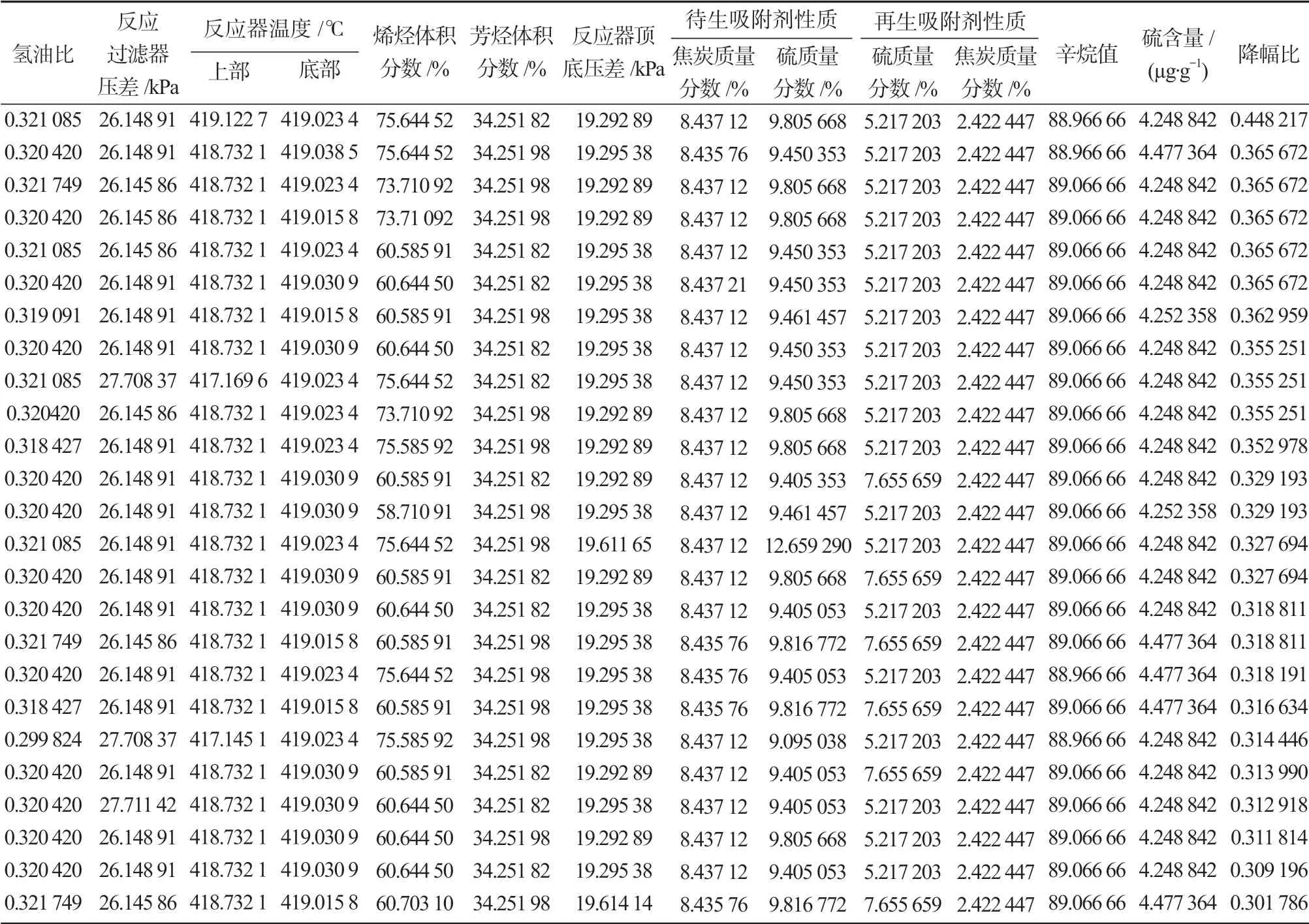
表5 符合条件的优化方案Table 5 Satisfactory optimized schemes

当某一变量逐步优化，其他变量不变时，辛烷值增加量与优化步数之间的变化情况如图9a和9b所示。由于再生吸附剂性质硫优化迭代步数较多，因此通过图9b 展示。由图9 可以看出，辛烷值增加量的变化与氢油比、反应器底部温度和反应器顶底压差变化呈正相关；随着变量反应过滤器压差值越接近最优理想状态，对辛烷值的影响变弱；辛烷值增加量变化与反应器上部温度变化呈先负相关后正相关的关系，且变化趋势大致相同，而待生吸附剂中的焦炭含量对辛烷值变化影响相反；辛烷值增加量与烯烃含量变化呈不断抖动的影响关系，正负相关性交替出现；辛烷值增加量与芳烃含量呈近似指数变化的正相关关系，且越接近最优状态影响越明显；再生吸附性质（焦炭含量）对辛烷值增加量产生不断交替的正负相关性，但总体呈微弱的正相关性；辛烷值增加量与再生吸附性质（硫含量）呈倒二次函数变化趋势；原材料对产品辛烷值增加量的影响呈现出负相关的特性，且随着其值逼近最优值，对产品辛烷值增加量的负向影响力度愈加强烈。由图9c 可知，当所有主要变量同时进行优化时，主要变量对辛烷值增加量的综合影响可以分为两个阶段，从一开始的初始状态到第10 次迭代，对辛烷值增加量的变化影响明显；第10 次迭代之后，对辛烷值的影响虽然仍然是正相关，但其影响程度下降了很多，其中一个原因是有些变量已经达到最优解。

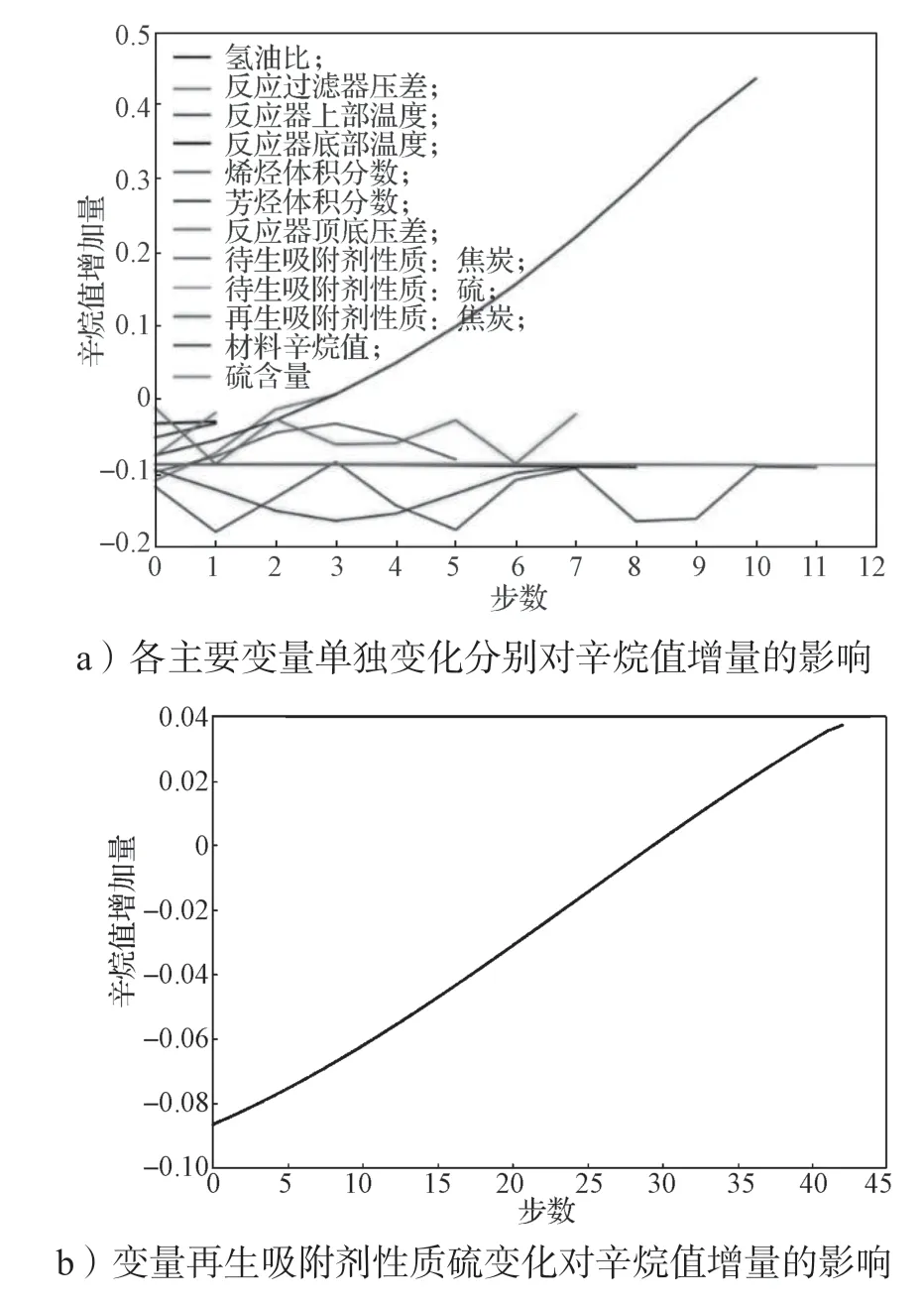
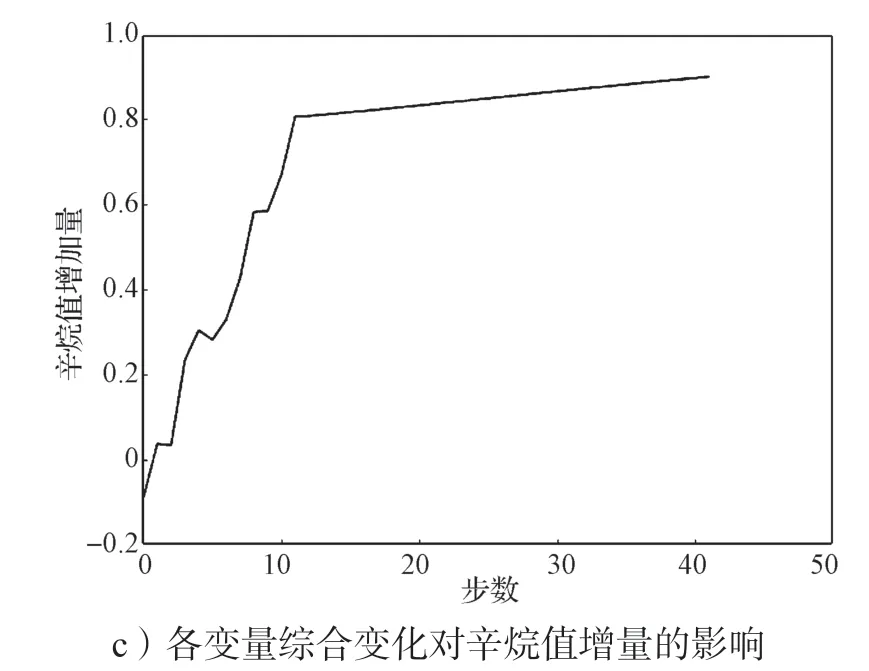
图9 各主要变量变化及辛烷值增量变化轨迹图Fig.9 Trajectories of major variables with their octane numbers

5 结语

本文通过层次聚类的方法，对预处理后的原数据集进行降维处理，建立基于BP 神经网络的辛烷值损失预测模型，对辛烷值损失及其指标进行预测；使用遗传算法迭代得出辛烷值损失降幅比大于30%的优化方案及最优优化策略，并通过可视化将各个操作变量的变化轨迹展示出来加以分析。实验结果表明，使用非线性层次聚类法比使用线性聚类法效果更好，能够很好地对数据集进行降维，降低了神经网络模型的训练与收敛难度。预测模型经过2 048 次迭代后，神经网络模型的损失函数下降趋势基本稳定。在数据集上，采用8:2 的比例构建训练集和测试集，并在测试集上达到了9.982 6×10-6的误差精度，能满足模型预测的要求和精度。根据样本硫含量不大于5 μg/g、主要操作变量的取值范围，以及13 个主要变量的变化步长，利用遗传算法迭代得到最优的参数集合。从集合中找到子代满足辛烷值损失降幅比达到30%的样本并排序，得到全部优化方案以及最优优化方案。在最优方案中辛烷值损失的降幅比达到44.822%，且各主要变量最优值均处于合理取值范围内。结果表明，本文所采用的数学模型与优化算法可以很好地对辛烷值损失问题进行预测与优化。