基于Rubinstein讨价还价模型的大件运输定价策略

张世良，涂晓红

1 研究背景

随着各类能源、石化、海洋工程等大型项目建设的增加，大型关键部件产地与工程建设布局的分离产生了大量的大件运输需求，超高、超长、超宽、超重等特征且不可解体的大件货物运输需求逐步增加，大件运输承担国家重大工程项目物资供应的重任，运输服务质量与运输效率会直接影响工程建设进度。截至2020年8月底，湖南省交通运输厅该年度已经办理大件运输许可4.3 万件，日均审批大件货物运输件数400 余件①湖南省交通运输厅http://jtt.hunan.gov.cn/jtt/hnglj/gzdt_1/202009/t20200921_13745362.html，大型项目建设的数量增加，大件货物运输需求增长加速。大件运输因超限等特性，陆地公路运输需要考虑公路高空路障、路面宽度与转弯半径等详细参数，水路运输需要考虑船舶吨位与等级，可能存在影响交通秩序、损坏道路桥梁等交通设施的现象。提升大件运输供给与服务能力、保障大件运输需求及时响应，对于促进能源、石化、海洋工程等重大项目建设具有重要意义。

相比于普通货物专线运输、集货配载、快递配送等运输方式，大件运输具有货物价值高、运输难度大、操作复杂程度高等特征，大件运输对于运输工具选择、运输路线策划、运输过程管控能力、运输异常问题处理等方面具有更高的要求，加上大件运输方向单向性、运输组织特性，多因素综合影响造成大件运输成本较高。大件运输需求方多为大中型装备制造企业，对于大件运输供方选择、定价方式管理流程相对成熟，往往采取寻源比价、竞争性议价、议标采购等方式进行发包，在大件运输供需业务谈判中具有一定优势。大件运输以设备专用性、路线唯一性等特征响应需求，大件运输企业亟需承接更多的业务来提升设备利用率，并分摊设备折旧费用，导致在大件运输需求服务中处于较为弱势地位，甚至出现违规承运等不良现象，给大件运输及重大工程项目物资供应带来潜在风险。大件运输过程及发包过程复杂，研究大件运输定价对于提升大件运输需求发包效率具有重要意义，运用科学合理的大件运输定价策略，可以规范大件运输发包价格，快速响应大件运输需求，有效保障大件运输交付。

2 研究综述

大件运输因货物质量、尺寸等超限导致运输难度较大，故对运输过程管控要求严格。许多学者研究了大件运输的复杂性，如卢英志等[1]将大件运输与传统货运运输进行比较后得出结论，大件运输具有服务链条长、运输风险大、物流效率低和专业要求高等特点；葛锋[2]指出，大件货物具有长大、笨重的特点，运输制约因素较多、风险高，现阶段铁路搭建货物运输存在送达时效较慢、铁路大车使用率较低等问题；荣晓凤[3]指出，由于从事大件运输的相关物流企业信息化与安全管控水平较低，在大件运输方式、大件运输专用设备、大件运输线路勘测等方面缺乏科学、便捷的方式，多为凭借经验制定运输方案，运输安全无法得到保证；刘丑宏等[4]认为大件货物运输车辆通行时会占据道路空间资源、增加车辆间干扰而导致路段运输服务水平降低，运用车辆折算系数等量化大件运输活动对道路交通影响。当前物流服务定价以成本加成等方式进行，需要借鉴一定的同类运输实施经验，不适用于运输需求异常、重复性低的大件运输，丁俊发[5]指出，我国物流业经历了计划经济下的政府定价，除邮政、铁路货运、管道运输、航空货运执行国家规定的指导价外市场自由定价；黄玮青等[6]在阐述铁路运输平均成本定价法、边际成本定价法、负担能力定价法和供求关系定价法的内涵及适用范围的基础上,提出铁路快运物流定价模型给出“门到门”和非“门到门”服务价格确定方法与原则，并指出定价模型存在信息采集难、信息分析应用能力不足等问题；朱文娟[7]认为公路货运物流服务价格结构以燃油费、通行费及人工成本为主，折射出物流价格构成不合理、不具竞争优势、定价机制扭曲、定价管理制度不健全等问题。由此，鉴于大件运输难度大，影响物流价格的因素较多，现有线性定价方式在一定的大件运输定价过程中存在局限性。

针对大件运输渠道选择与定价可能需要进行采购议标、竞价谈判等方式，许多学者运用纳什博弈等理论研究了竞价投标，如S.Nataraj 等[8]认为，运输企业通过投标或者报价这种反向拍卖的方式来获取业务，探讨运用预测和统计学习的方法来确认合适的价格以提升投标竞争力，采用时间序列分析进行成本预测，并且根据历史数据发展统计学习模型，从而预测投标成功的概率；马永刚[9]指出，物流服务议标实质是相关参与方的博弈过程，每个参与方对自己行为的选择必须以对其他参与方将如何反应的判断为基础，运用贝叶斯-纳什均衡的博弈论，构建竞价博弈模型，提高快速报价能力和中标率；王小胜等[10]基于克服先动优势的讨价还价模型，并结合利益分配博弈和差额分摊博弈，分析了分享型合同节水管理的利益分配问题，得到趋于合理的节水利益分配方案，表明参与者的利益分配额与固定成本、贴现因子、消耗因子等密切相关；王道平等[11]制定讨价还价模型下的生鲜产品保鲜成本共担契约，供应链零售商与供应商博弈，约束对方的决策，相比传统的成本分担契约，零售商分担的保鲜努力成本增加，供应商提供更高的保鲜努力水平，消费者意愿支付价格随之提高，产品变质损耗降低，供应商和零售商的利润增加；黄毅祥等[12]指出，电力市场交易机制由“一对多”竞价上网变为“多对多”讨价还价匹配，因而削弱了售电侧博弈主体的相对议价能力，发电商群体在博弈过程中将索取更多的消费者剩余，发电侧整体报价上涨，需要完善信息传输渠道，保障电力市场交易信息的实时性与公开性，构建完全竞争的电力市场。可见，运用博弈论[13]研究招投标报价以及合作双方利益分配问题，具有一定的理论与现实意义。

3 构建大件运输需求商与承运商讨价还价模型

3.1 模型假设

1）理性经济人假设。参与大件运输讨价还价的各潜在供应商都是理性的经济人，以追求自身利益最大化为行动目标。

2）完全信息假设。假定参与大件运输讨价还价的多家参与方均收到了需求方提供的大件运输需求；需求方将大件货物运输起止点、大件货物特征等信息无差别地传递各参与方；参与方之间不存在信息沟通，信息完全独立，并按照需求信息进行运输路线、包装方案等成本要素策划，进行成本测算及报价，并将报价结果提供给需求方。

3.2 承运商之间的竞价过程

需求方就某项大件运输需求进行供应商选择与议价，由于消除单一性采购等目的，往往通过询比价、邀请议标、公开招标等方式获取最优采购价格，有i（i∈N*，且i＞1）家潜在承运商具备大件运输承运能力且有合作意愿，i家潜在承运商根据运输需求进行运输路线勘探、包装方案设计以及成本测算，各潜在承运商根据运输成本测算结果Cj（Cj＞0，第i家报价）进行运输报价Pi（Cj＜Pi）。假定除价格因素外，其他技术质量、交期等因素同质化，无需进行综合评价，需求方组织i家潜在承运商按询比价、邀请议标、公开招标等方式进行相互竞价，经过多轮次竞价后，部分潜在承运方不再下调价格而选择放弃继续议价，存在j（i∈N*，且i＞j≥1）家潜在承运商提供最低报价Pm。

3.3 需求方与承运商讨价还价过程

需求方根据运输需求进行价格预测，将上限价格设置为P，以此为基准与潜在承运商进行议价，此时，存在3 种情况：

1）当P＞Pm，潜在承运商报价低于上限价格，需求方可能接受j家报价（当j＞1 时需进行议价份额合理分配；当j=1 时，由独家承运），需求方与承运商之间讨价还价结束；

2）当P＞Pm时，需求方不接受潜在承运商报价；

3）当P＜Pm时，潜在承运商报价高于上限价格，需求方不接受潜在承运商报价。

处于后面两种情况，则进入需求方与承运商之间第二轮“出价-还价”过程。

运用Rubinstein 讨价还价模型对需求方与潜在承运商合作的利润进行博弈分析，制定分配合作利润进行讨价还价。需求方与潜在承运商具备一个前提条件，假定约定合作最终得到的合理剩余利润为π，需求方期望得到的合作剩余分配比例为Rx，而潜在承运商期待合作剩余得到的比例为Ry，且存在Rx+Ry≤1，需求方与潜在承运商均为理性人，且信息相互独立，讨价还价过程中倾向于合作而不是谈判破裂，都是追求利益最大化。在需求方与潜在承运商的讨价还价过程中，当时，需求方对合作剩余利润的分配逾期小于最后能获得的比例，则该合作无法达成，因为需求方与潜在承运商都倾向于自身的最优选择；只有当时，合作才能实现。假设需求方与潜在承运商对获取合作剩余分配的比例Rx、Ry的心理预期服从区间[a,b]（0 ≤a＜b≤1）的均匀分布，在动态的讨价还价中，需求方与潜在承运商会按照对方接受或拒绝报价而灵活调整自己的行为，从而调整对合作剩余预期比例的估值，如当需求方在第一阶段报价为P，则潜在承运商调整Ry，此时Ry服从区间[P,b].

第二轮讨价还价时，制造商“出价”提出分配剩余利润的分配方案，若潜在承运商选择接受该方案，则讨价还价结束。在第二轮讨价还价过程中需要考虑时间因素即贴现因子φx和φy，由于讨价还价是在第二轮实现合作的，双方收益都存在被折扣，否则双方都会倾向于继续讨价还价，此时需求方与潜在承运商得到的收益分别是、。如果潜在承运商不接受第二轮讨价还价中需求方“出价”，则进入潜在承运商“还价”开始第三轮博弈。以此类推，直到第n轮讨价还价中双方达成满意的结果。博弈的最终结果取决于“出价”次数：n/2（n∈N*，且n为偶数）或n+1/2（n∈N*，且n为奇数），前者为需求方 “出价”，后者为潜在承运商“出价”；经讨价还价，最终出价为时，需求方与潜在承运商收益分别是、，若最终报价时另一方不接受，则合作无法达成，双方收益都为0。根据上述逻辑。将需求方与潜在承运商讨价还价过程描述如图1 所示。

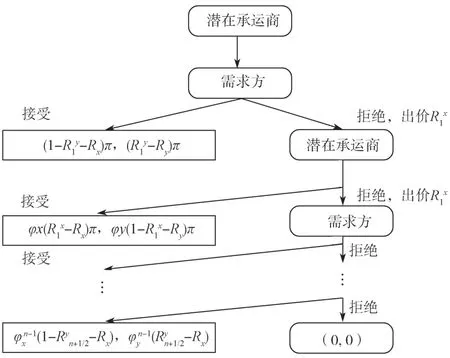
图1 需求方与潜在承运方的讨价还价过程Fig.1 Bargaining process between the demander and the potential carrier

3.4 需求方与承运商讨价还价模型求解

在第二阶段讨价还价中，若潜在承运商拒绝需求方的“还价”结果，则谈判破裂，双方收益均为0。双方趋于合作时，简化为

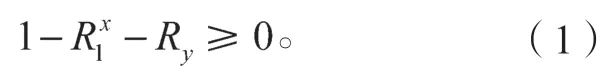
此时，潜在承运方接受合作，而不再考虑竞价结果，此时需求方收益为，而此时潜在承运商收益为；对于需求方而言，评估潜在承运商在第二阶段讨价还价的选择策略，即潜在承运商以为最低标准。在“出价”“还价”过程中，需求方与潜在承运商互相根据对方反应更新后续策略，从自身利益最大化出发，需求方以利润最大化为目标，即

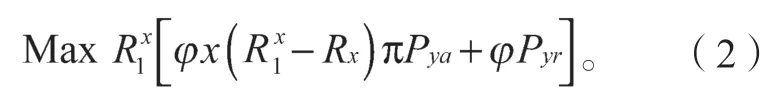
在式（2）中，Pya、Pyr分别对应潜在承运商接受“出价”或拒绝的概率：

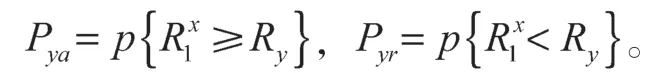
根据需求方对潜在供应商在讨价还价过程中的出价，改变了其对合作剩余分配的预测，即认为Ry服从的均匀分布。得出如下概率：将式（3）代入式（2）可得

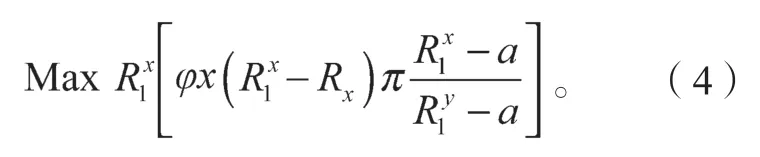
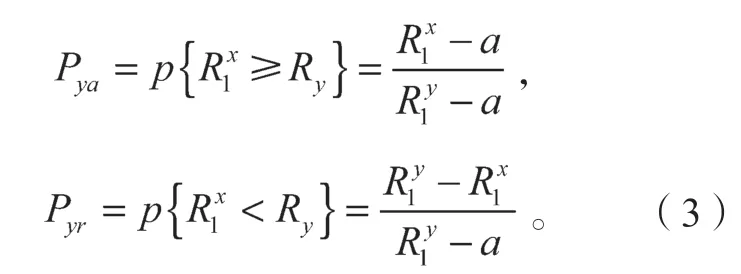
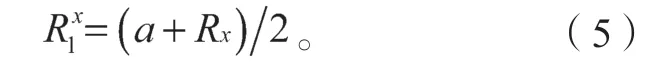
若在第二阶段达成合作，结束讨价还价，则潜在承运商接受需求方的合作剩余分配比例为，此时可得需求方收益为，潜在承运商收益为。

在第一阶段，基于需求方角度，若讨价还价进行到第二阶段，需求方收益为；为实现此收益，其在第一阶段讨价还价接受潜在承运商报价的条件为，经简化可得

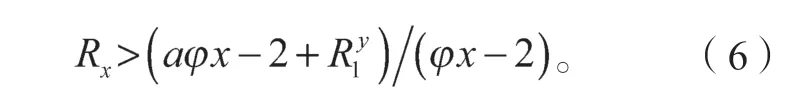
与此同时，潜在承运商根据需求方在第一、第二阶段“出价”与“还价”的情况，从理性经济人假设角度考虑，坚持在“出价”时，可以实现利益最大化，其收益为

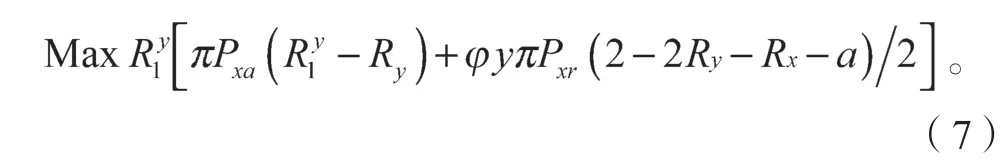
式中Pxa为需求方在第一阶段接受出价的概率，并且

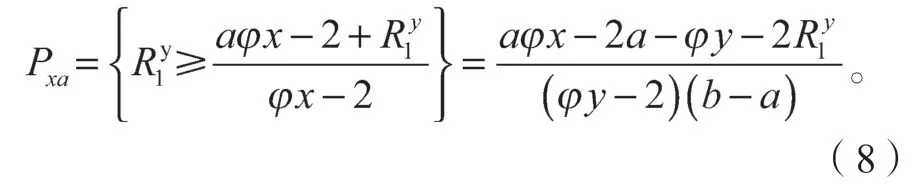
Pxr为需求方在第一阶段拒绝潜在供应商出价，但在下一阶段潜在承运商接受的概率，且

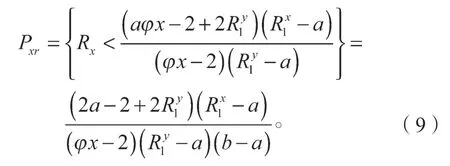
根据上述结果，将式（8）～（9）代入式（7）中，可得：

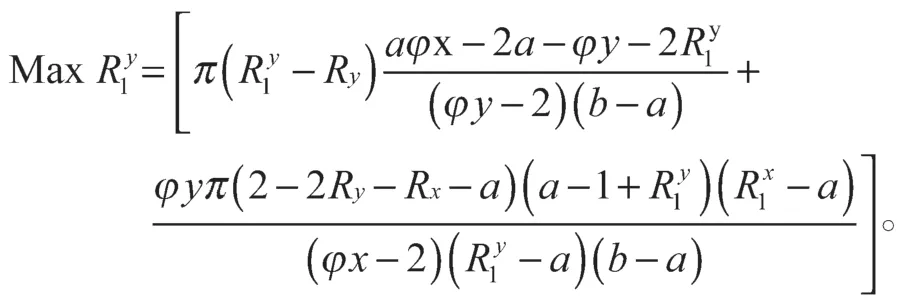
式中φx+φy≤1、a＜φx＜b、a＜φy＜b，潜在承运商实现利益最大化，则对求导，则得到潜在承运商在第一阶段的最佳出价为

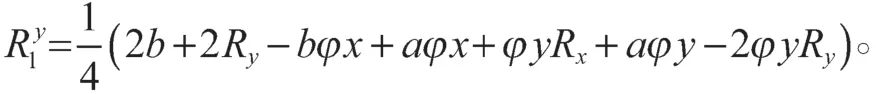
在上述讨价还价过程中，需求方与潜在承运商是否达成合作的关键，在于双方的贴现因子大小，以及各自对剩余分配预期等因素。在信息不对称的大件运输需求发包中，需求方要建立严禁的供应商选择程序，对潜在承运商的服务能力、服务质量进行判断，然后选择优质供应商，由此需要提升需求方对需求信息的透明度，以便更加有效地进行供应商选择与匹配。

4 大件运输服务定价策略建议

相比普通货物运输按照公里数、运输质量等线性定价方式，通过讨价还价模型证明大件运输定价存在更多的影响因素，因而潜在承运商选择及定价变得更加复杂化，而潜在承运商需要针对大件运输特性进行更多的前期运输策划，投标报价等环节变得更加谨慎。根据Rubinstein 讨价还价模型分析，对于大件运输服务定价策略给出建议：

1）需求方提供完整的大件运输需求信息，包含大件货物的尺寸、货物质量、包装防护要求、装卸作业量等物流成本等相关要素，并根据运输相关要素进行成本估算且制定竞价最高限价，形成对议价结果的参考基准。各潜在供应商根据需求方给出的运输需求信息以及相关要素制定完整的运输策划、运输线路勘探、异形包装设计等等，根据运输策划、方案及保障产生的物流作业要素准确测算运输成本，按照成本增加一定比例利润或其他方式进行精准报价。实现潜在供应商准确测算运输成本，需要强调需求方提供准确且详细的运输需求信息，避免后续讨价还价中增加价格影响因素而影响双方预期，导致不必要的多阶段讨价还价。

2）在讨价还价过程中，需求方与潜在承运商“出价”-“还价”的阶段数越多，剩余分配的比例就越低，需求方倾向于更早地完成讨价还价并达成合作。需求方在组织潜在承运商竞价时，通过准确的运输需求输出尽可能地吸引更多的参与方，以公布竞价排名或结果等方式向各参与方施加压力，获取更低的竞价结果，促进双方在第一阶段讨价还价中获取有利的结果。潜在承运商之间的竞价结束后，将竞价结果或者更低“出价”与需求方进行讨价还价，本身具备先动优势，根据需求方接受或者“还价”信息进行第二轮“出价”，尽量在三阶段讨价还价中达成双方能接受的结果。

3）需求方与潜在承运商对于“出价”-“还价”的结果，取决于对另一方心理预期的准确判断与耐心程度，通过对方“出价”或者“还价”的信息来动态调整后续“出价”、“还价”，有利于尽快达成可接受的议价结果，提升具有信息优势一方的议价能力。在实际招议标等议价过程中，需求方往往约定出价还价次数，采取一次或二次报价方式，避免陷入无限次循环报价。

5 结语

构建需求方与潜在承运商在大件运输外包过程中讨价还价定价策略，需要需求方充分释放大件运输需求相关信息，潜在承运商根据获取的信息策划大件运输方案并根据方案作业要素核算运输成本，具有一定的理论意义与可行性，为潜在承运商在需求方询比价、竞争性议价、议标等方式中提供报价策略建议。在实践过程中对于相关影响因素、双方心理预期、需求方上限或承运商竞价结果等信息获取存在局限性，需要通过进一步的量化数据研究来提升模型应用的实践性。