半刚性基层沥青路面结构高速弯沉仪应用误差

吴朝阳，蒋 鑫

（1.西南交通大学土木工程学院，四川 成都 610031；2.西南交通大学道路工程四川省重点实验室，四川 成都 610031；3.西南交通大学高速铁路线路工程教育部重点实验室，四川 成都 610031）

沥青路面路表弯沉能反映路面结构的整体强度和刚度，与路面结构的使用状态有密切联系，故成为道路检测的关键指标之一[1].传统的低速间断式弯沉测试手段包括利用贝克曼梁测试静态荷载作用下的回弹弯沉，利用落锤式弯沉仪（falling weight deflectometer，FWD）测试脉冲荷载作用下的动态弯沉等，但均存在周期长、效率低、交通影响大、安全风险高等缺陷[2].为达到在真实车辆荷载作用下高速、连续测量路表弯沉的目的，近年来研究人员利用多普勒效应原理，巧妙地实现了高速运动状态下对路表弯沉信息的间接测量.即在检测车辆上安装多个多普勒测振仪传感器，通过测量高速移动检测车辆荷载作用下路面结构弯沉盆内、外传感器的差异，先获得高速移动荷载作用下路面垂向变形速度，随后对路面变形速度曲线积分进而得到弯沉曲线[3].基于多普勒效应原理，世界各国先后研制了高速弯沉仪（traffic speed deflectometer，TSD）[3]、激光动态弯沉仪（laser dynamic deflectometer，LDD）[4]等多种高速连续弯沉检测设备.其中，TSD 设备研发始于20 世纪90 年代末，具有高速（高达90 km/h）、无须封闭交通、可获得连续高分辨率弯沉信息等优点，其第二代设备经美国公路战略研究项目二期（second strategic highway research program，SHRP2）[5]和美国联邦公路管理局（Federal Highway Administration，FHWA）[6]验证，已在美国、英国、澳大利亚、意大利、波兰、南非和中国等国家应用，并逐步获得大规模推广.但注意到，美国等西方国家普遍采用常用式、深厚式和全厚式等沥青路面结构，这些路面结构整体弯沉较大，一般认为弯沉盆的范围小于7 m.TSD 在研制时即假定弯沉盆的范围小于7 m，距离荷载作用范围3.5 m之外的路面垂向变形速度忽略不计，测量模型采用弯沉盆之外传感器的读数作为参照，校正其它位置传感器读数[3,7].同时，因荷载作用点双轮组轮隙中心处的弯沉值为极值点，认为最大弯沉值处路面垂向变形速度也忽略不计.

因国情不同，我国的沥青路面设计重视“强基薄面”思想，多采用以半刚性基层为主的沥青路面结构[8-9].相比较常用式、深厚式和全厚式等沥青路面结构，半刚性基层沥青路面结构的基层为承重层，弹性模量很大.不难想象，半刚性基层路面结构整体弯沉较小，弯沉盆的范围相对较大.故如将TSD 直接应用于测试半刚性基层沥青路面结构的变形速度，其测试误差如何尚不得而知，针对半刚性基层沥青路面结构的路表垂向变形速度分布规律、测试误差有待进一步深入研究.基于我国开展高速无损检测技术的迫切需要，本文尝试探讨TSD 移动荷载作用下半刚性基层沥青路面结构的路表变形速度规律，评估TSD 设备应用于半刚性基层沥青路面结构中潜在的测试误差.

1 TSD 系统组成及激光多普勒测试原理

如图1 所示，TSD 高速激光弯沉检测系统由承载车、多普勒激光测振仪系统、检测控制系统、温度控制系统和数据处理系统等组成[3].其中，多普勒测振仪系统为核心装置，可连续监测移动负载附近的路面结构变形速度.

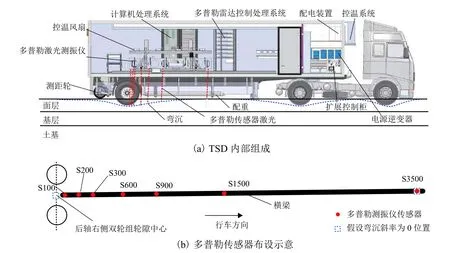
图1 TSD 设备内部组成及多普勒传感器布设示意Fig.1 Innteral componets of TSD and placement of Doppler sensors

以编号为TSD9 的高速弯沉仪为例，其后轴轴载为100 kN，以后轴载右侧双轮组轮隙中心为起点，沿行车方向布设7 个激光测振仪传感器测量路表变形速度.多普勒测振仪传感器距后轴载双轮组轮隙中心的距离分别为0.1、0.2、0.3、0.6、0.9、1.5 m 和3.5 m，对应的传感器名称分别为S100、S200、S300、S600、S900、S1500 和S3500.其 中，S3500 作为参照传感器，用于校正其它6 个传感器的读数.

多个多普勒激光测振仪安装于特制的刚性横梁上，如图2 所示.由于路面的垂向变形速度远远小于车辆移动过程中横梁的变形和不规则运动，TSD 通过精密的伺服系统和惯性系统持续监控多普勒传感器的位置控制误差.横梁不规则运动引起的测速误差由横梁上3 个正交的激光陀螺仪补偿.为保证多普勒激光测振仪的精度，多普勒测振仪发射的激光与路面法线的交角需小于2°[2-3].为控制温度对横梁变形的影响，整个横梁装置使用空调控温，维持横梁的温度恒为20 ℃.

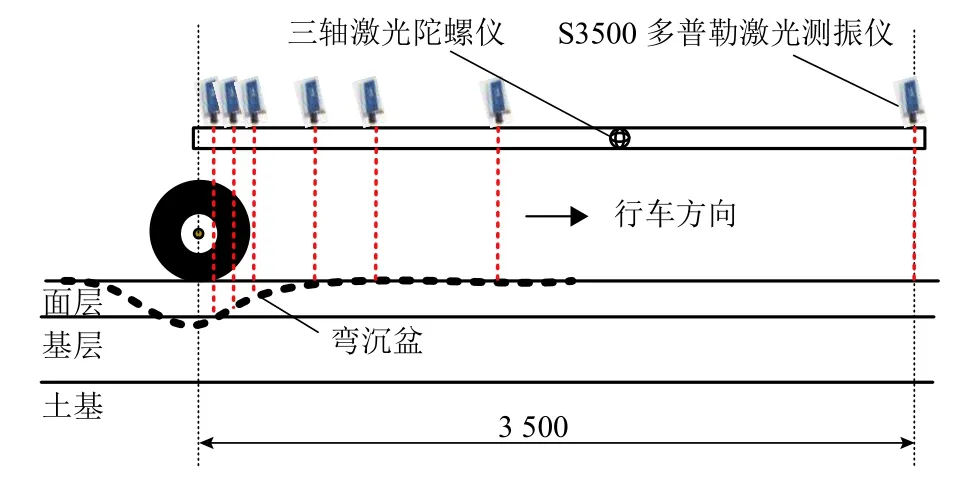
图2 多普勒激光测振仪系统工作原理Fig.2 Working princliple of laser Doppler vibrometer system

TSD 以速度Vh移动的过程中，发出一束频率为f1的激光到路表，反射激光频率将变化为f2.多普勒激光传感器可测得发射频率f1和反射频率f2的变化，并计算测试路表的垂向下沉相对速度，即弯沉速度Vv，如式（1）所示[3].

式中：λ为发射激光波长.

TSD 测量车测得的弯沉速度需要转化为弯沉斜率S[3]，如式（2）所示.

依据上述原理，TSD 设备可以在高速移动的情况下连续测量路面的变形速度，根据三次样条插值分段Hermit 插值（piecewise cubic Hermite interpolating polynomial，PCHIP）方法可将直接测试得到的路面变形速度转换为弯沉[10]，如图3 所示，x和yx分别为距后轴轮隙中心距离和弯沉，从S3500 传感器开始到后轴轮隙中心，根据实际测振仪位置点将整个弯沉斜率曲线分为7 段，分段进行Hermit 三次多项式函数插值拟合.从微积分意义上讲，弯沉速度曲线的定积分为对应点的弯沉值，通过累加各段的面积即可得到最大弯沉值.

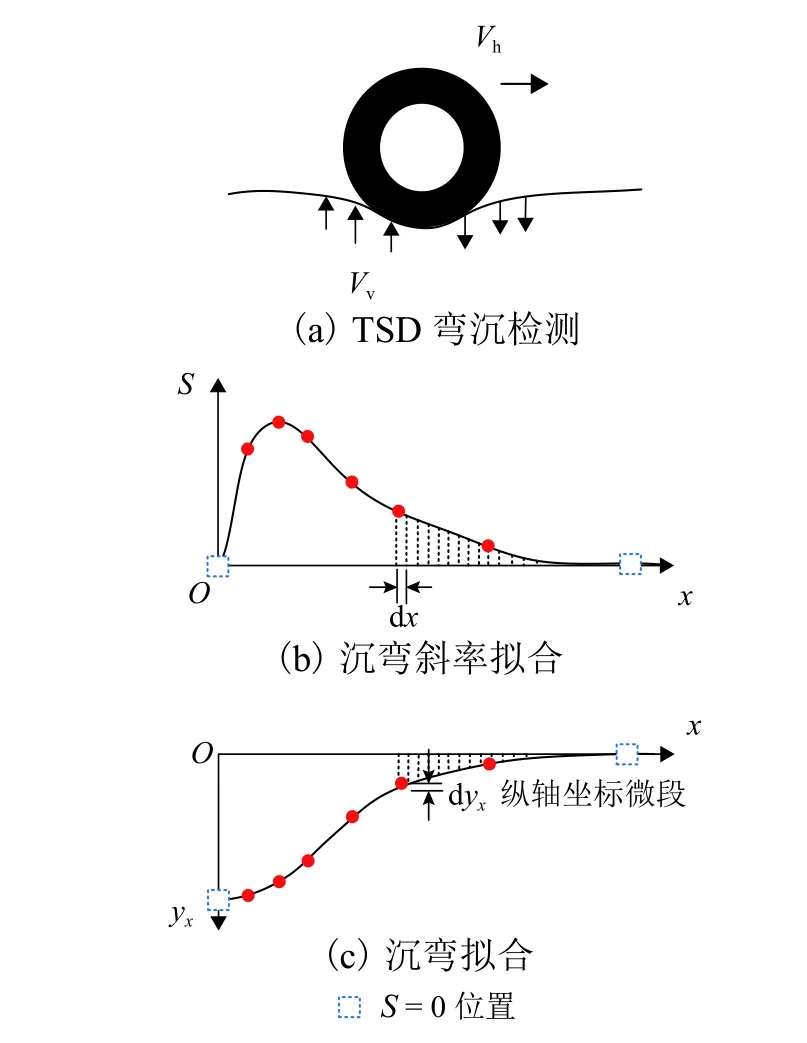
图3 TSD 弯沉拟合方法示意Fig.3 Fitting method of TSD deflection test

2 2.5D 有限元程序可靠性校验

3D 有限元可获得移动荷载作用下沥青路面结构的力学响应，但耗时长、建模复杂[11].2.5D 有限元法具有计算高效准确、可扩展性强等优点[12-13]，笔者前期利用FORTRAN 语言已成功开发了适用于沥青路面结构动力计算的2.5D 有限元程序[14]，下面分别结合国外传统式基层、国内常用半刚性基层沥青路面结构进一步验证所开发程序的可靠性.

如图4 所示，美国MnRoadCell 19 路面结构[6]为传统式基层沥青路面结构，视为线弹性体，各结构层的弹性模量E、泊松比μ和密度ρ等材料参数一并列于图中.荷载的移动速度为46.3 km/h，轮胎-地面接触应力为不均匀分布[15].建模时考虑到结构的对称性，取半结构进行分析，以节约计算资源.选用矩形单元离散模型，靠近荷载区域网格大小为0.02 m×0.02 m，远离荷载区域网格最大为0.03 m×0.08 m，共划分1978 个单元.路面各结构层阻尼均为0.05，模型右侧设置为黏滞边界[14].

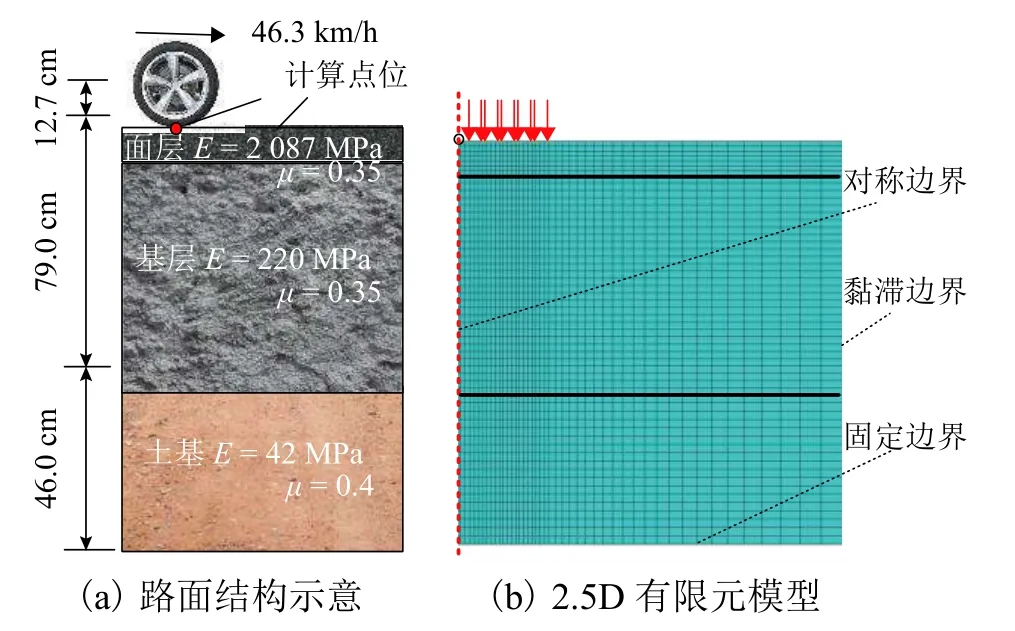
图4 MnRoadCell 19 路面结构及2.5D 有限元模型Fig.4 Pavement structure of MnRoad Cell 19 and 2.5D finite element model

2.5 D 有限元与参照文献[6]中已给出的利用3D 连续有限层法3D-MOVE ANALYSIS 程序计算结果进行了对比.路表弯沉计算结果如图5 所示，由图5 可见，两者结果趋势保持一致，吻合相对良好，峰值点非常接近，这充分说明所开发的2.5D 有限元程序具有极高准确性.

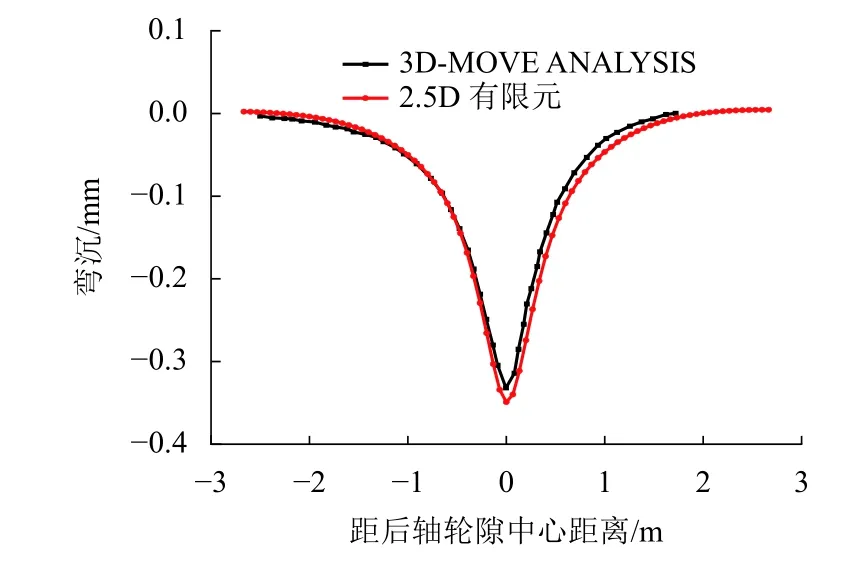
图5 2.5D 有限元与3D-MOVE ANALYSIS弯沉计算结果对比Fig.5 Calculated result comparison between 2.5D finite element modeland 3D-MOVE ANALYSIS

另一方面，文献[11]开展了三向非均布移动荷载作用下半刚性基层沥青路面结构的3D 有限元计算，其路面结构厚度、材料参数[11]如表1、2 所示，表2中的 τ、g分别为沥青面层松弛模量主曲线转化得到的Prony 级数中的松弛时间、无量纲系数.采用2.5D 有限元程序对此案例进行再次分析，荷载与文献[11]完全相同，均为移动速度为35 km/h 的双轮荷载.

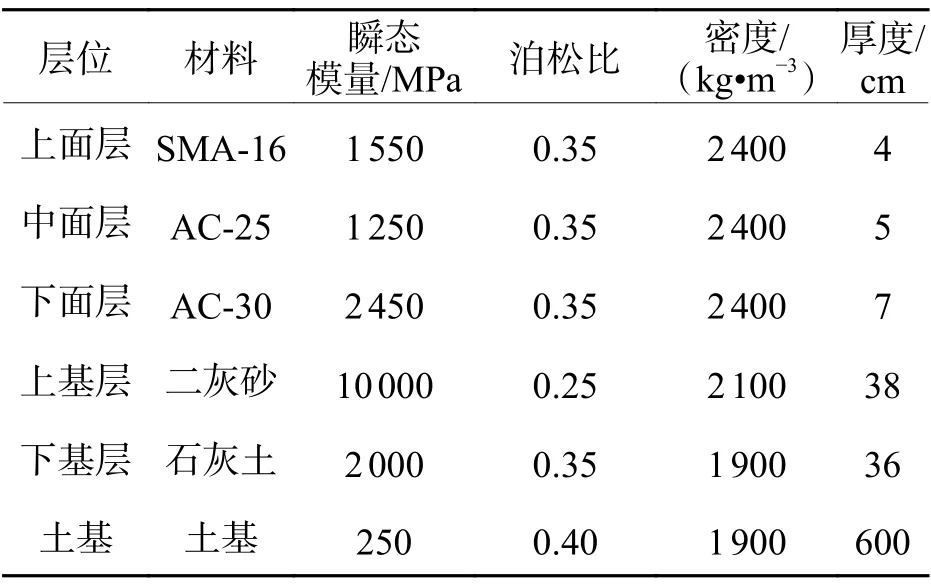
表1 路面结构材料参数表Tab.1 Material parameters of pavement structure

表2 沥青混合料Prony 级数参数Tab.2 Prony series parameters of asphalt mixture

图6 为中、下面层横向应变时程曲线2.5D 有限元与3D 有限元的对比结果.可以看出，2.5D 有限元结果与文献[11]结果趋势一致，峰值相对误差仅为4.53%，这再次证实本文所采用的2.5D 有限元程序完全可应用于国内常用半刚性基层沥青路面结构的力学分析.

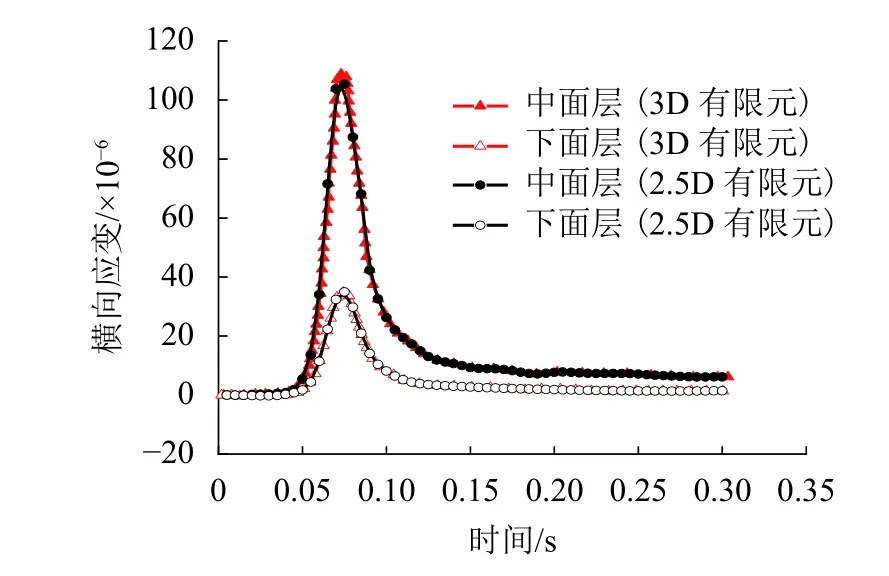
图6 2.5D 有限元和3D 有限元模型计算结果对比Fig.6 Comparison between 2.5D and 3D finite element model for semi-rigid pavement structure

3 半刚性基层沥青路面结构弯沉斜率特征

现选定常用式、全厚式和半刚性基层3 种典型类型的路面结构，采用前述所开发的2.5D 有限元程序，对比分析3 种路面结构弯沉斜率曲线的分布特征，从而明确各种路面结构弯沉斜率分布的差异性.

常用式沥青路面结构选用曾开展TSD 测试的美国PA-144 路段和ID-22 路段[15]，全厚式结构选取美国US9 号公路上的某TSD 实测工点（US9-43），半刚性基层结构厚度选取四川成德南高速公路（CDN）半刚性基层试验段工点，结合实测数据及半刚性基层模量取值范围，材料参数取值如表3所示.TSD 荷载为单轴双轮组，轴重为100 kN，双轮中心距为34.3 cm，轮胎-地面接触应力为不均匀分布[15].计算时路段PA-144、ID-22、US9-43 和CDN 的荷载移动速度分别为71、89、80、72 km/h

表3 路面结构厚度及模量Tab.3 Parameters of asphalt pavement structure

3 种沥青路面结构路表弯沉斜率曲线如图7 所示.从整体上来看，常用式、全厚式沥青路面结构的弯沉斜率曲线均为一条平滑曲线，总体趋势表现为先上升后下降，仅有一个极值点，极值点的位置在S100～S300 之间，弯沉斜率曲线的峰值点数量级为0.1 mm/m 以上，弯沉斜率曲线读数常用式要大于全厚式，所得趋势与文献[16]的规律保持一致.而半刚性基层沥青路面的整体趋势表现为先上升后下降，而后再上升，再缓慢下降，整个弯沉斜率曲线存在多个极值点.因全厚式结构的模量从上往下依次递减，半刚性结构模量分布依次为面层较大、基层最大、土基模量最小，较大的半刚性基层模量对弯沉斜率曲线的形状影响较大.

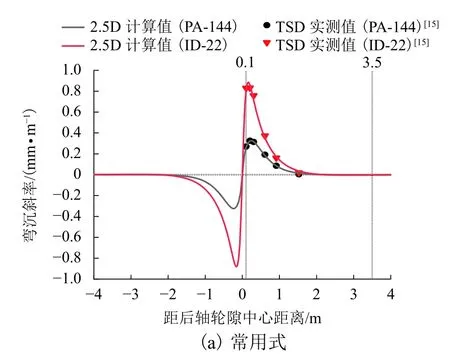
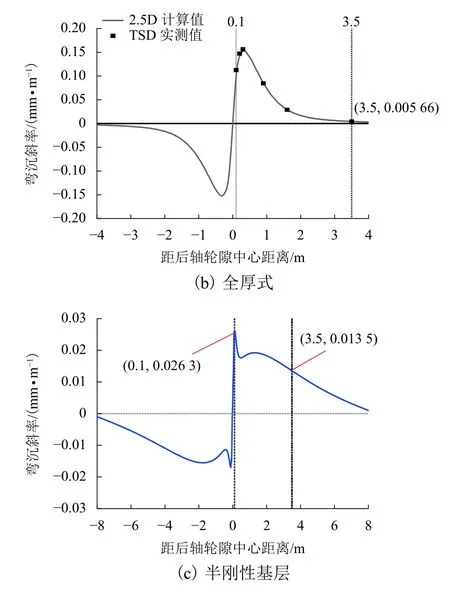
图7 3 种沥青路面结构弯沉斜率Fig.7 Deflection slope curves of three types of asphalt pavement structure under the moving load of TSD

4 半刚性基层沥青路面结构弯沉斜率误差评估及修正

前面分析可以看出，由于TSD 设计算法时假设3.5 m 处传感器的弯沉速度为0，在沥青路面结构变形较大的路面差异不明显，假设较为合理.但与常用式、全厚式结构不同，半刚性基层沥青路面结构S3500 位置处的弯沉斜率并不为0.这是由于半刚性基层沥青路面结构刚度较大，整体弯沉较小，荷载的传播范围相对更广，弯沉盆范围相对更大.半刚性基层沥青路面结构中S3500 位置传感器弯沉斜率为S100 位置传感器弯沉斜率的51.3%.如果以S3500传感器弯沉斜率校核其它传感器，势必会造成S100、S200、S300、S600、S900 和S1500 位置处的弯沉斜率变小，这与实际情况不符.弯沉斜率变小，对应的弯沉也会变小，如直接利用这种包含误差的测试结果，可能会过高地估计路面结构的刚度及其使用寿命，需在工程中引起足够的重视，因而，在半刚性基层路面结构开展网络级高速弯沉检测时，有必要对S3500 传感器假设引起的弯沉误差影响进行评估.下面详细讨论测试误差及消除误差方法.

首先将半刚性基层结构计算所获弯沉斜率曲线进行插值得到S100、S200、S300、S600、S900、S1500和S3500 传感器弯沉斜率，然后直接利用其它传感器弯沉斜率减去S3500 位置弯沉斜率，最后利用PCHIP方法得到拟合弯沉曲线，如图8 所示.对比利用2.5D 有限元方法得到的计算弯沉和利用PCHIP 方法拟合弯沉曲线，两者弯沉最大值差异为87.3%.需要进一步说明的是，从理论上讲，直接通过其它传感器弯沉斜率减去参考传感器弯沉斜率即可得到真实的路面变形速度，但由于横梁运动旋转导致的不同测振仪的旋转角度和旋转半径不同，实际上需要实时计算测振仪的旋转角度和旋转中心进行误差消除，实际误差可能更大.

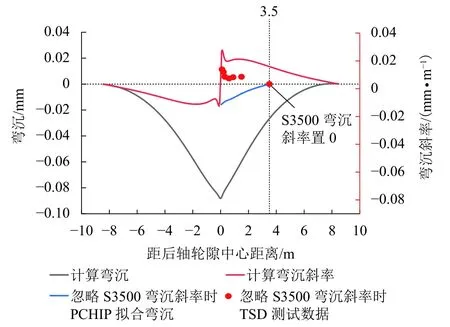
图8 忽略S3500 传感器弯沉斜率时计算弯沉和拟合弯沉的差异Fig.8 Difference between fitting deflection and calculated deflection in the case of ignoring of S3500 sensor deflection

因半刚性基层沥青路面结构计算弯沉和拟合弯沉存在较大差异，其主要原因在于校正读数的S3500 传感器位于弯沉盆内.S3500 位置处的传感器主要是受土基模量Es的影响[17].假定Es分别为60、80、100、120、140、160、180、200 MPa，分析半刚性基层沥青路面结构中土基模量变化对S3500 传感器测量结果的影响，如图9 所示.由图9 可见，不同土基模量的S3500 位置处的弯沉速度均不为0.土基模量为200、140、120、60 MPa 时，S200 传感器弯沉斜率误差分别为26.3%、35.2%、39.7%和62.2%.土基模量越小，TSD 测试误差越大.因此需根据半刚性基层沥青路面结构弯沉盆的实际范围，适当延长TSD 横梁的长度，使参照传感器位于弯沉盆之外.从图9 还可以看出，在土基模量为60 MPa 的情况，假设参照传感器位于荷载中心4.5、5.0、6.0、8.0 m 时S200 传感器弯沉斜率误差分别为45.8%、37.9%、26.0%、5.8%，参照传感器位于距后轴轮隙中心8.0 m位置处才能满足工程精度的需要.

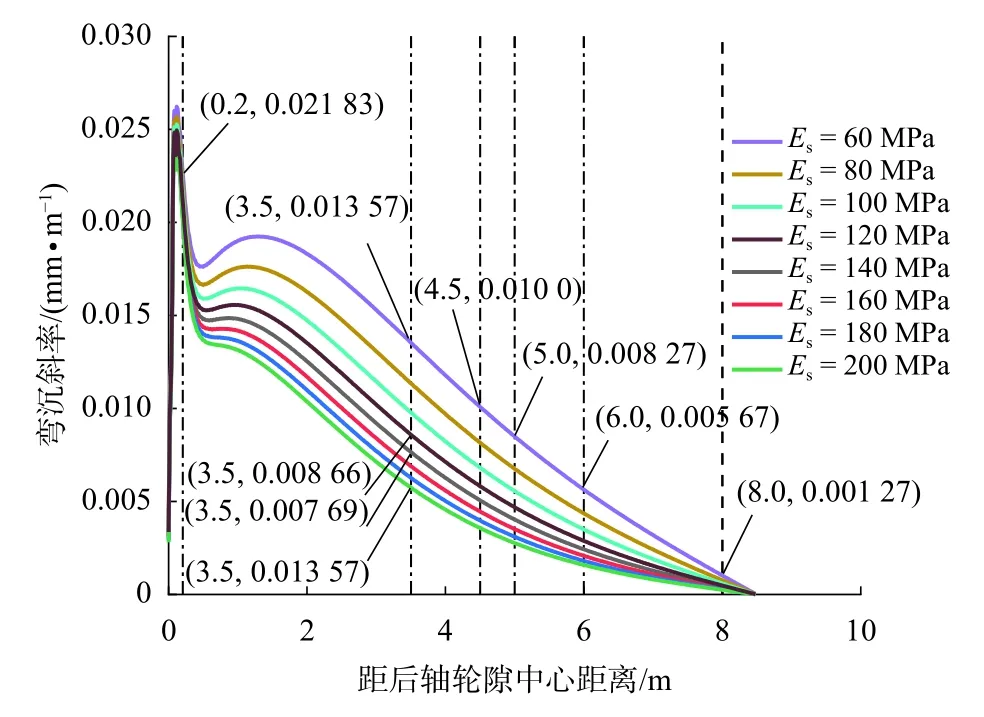
图9 半刚性基层沥青路面不同土基模量结构弯沉斜率曲线Fig.9 Influence of subgrade modulus on deflection slope in asphalt pavement with semi-rigid base

5 结 论

1）在TSD 高速移动荷载作用下，不同路面结构的弯沉斜率特征不同.常用式、全厚式结构仅存在一个峰值点，半刚性基层结构因基层模量大于面层模量，存在多个峰值点.全厚式结构弯沉斜率的峰值比半刚性路面结构大一个数量级.

2）当路面结构整体刚度较大时，距离后轴双轮组轮隙中心3500 mm 处的多普勒传感器的弯沉速度并不为0，忽略S3500 传感器读数在网络级测试中可能会造成较大的误差.由于原假设的不合理，可能会导致测得的路面结构弯沉斜率小于实际值，过高估计路面结构的刚度.

3）TSD 作为网络级路面检测设备，应用到半刚性基层沥青路面结构有一定的误差.半刚性基层沥青路面结构采用PCHIP 方法拟合后的弯沉与计算弯沉最大值差异为87.3%，需要在工程上引起足够的重视.