基于物元-阴性选择算法的轴箱轴承故障检测
2021-10-31赵聪聪刘玉梅赵颖慧
赵聪聪,刘玉梅,赵颖慧,白 杨
(1.吉林农业大学工程技术学院,吉林 长春 130118;2.吉林大学交通学院,吉林 长春 130022;3.一汽研发总院智能网联开发院,吉林 长春 130011;4.一汽大众汽车有限公司技术开发部,吉林 长春 130011)
轴箱轴承作为高速列车走行部的关键部件,其运行环境复杂,一旦出现故障会导致热轴、燃轴和切轴等事故,直接影响行车安全[1-2].轴温检测方法难以发现早期、微弱故障,基于振动信号的检测方法更为有效[3].但列车实际运行状态或加速试验的振动数据获取通常代价高昂,基于模型的仿真数据又难以保证精度,致使轴承故障数据获取困难[4].
Forrest 等[5]提出的阴性选择算法(negative selection algorithm,NSA)是借鉴免疫系统的自己-非己识别原理,进行异常检测时不需要先验知识,只需利用有限的正常样本生成检测器.NSA 算法具有较强的鲁棒性和并行性,适用于故障诊断和异常检测领域[6],但需要考虑检测器的生成和优化问题.可拓学以物元理论和可拓集合为理论支柱,从“质”和“量”两方面对问题展开研究[7-8],通过构建n维物元模型,实现对问题的多角度描述.
考虑NSA 算法在异常检测领域的优势以及物元模型的定性定量表述特性,本文提出了一种基于物元和NSA 算法的轴箱轴承故障检测方法,避免了故障数据不足的缺陷.构建检测器的n维物元模型,以检测器与训练样本之间的综合关联度作为匹配规则构建适应度函数,并利用粒子群优化(particle swarm optimization,PSO)算法生成候选检测器.为使检测器尽可能覆盖非己空间,在适应度函数中引入控制参数,并分析控制参数对检测器生成的影响.此外,为降低候选检测器集合的冗余度,制定了检测器特征参数区间的合并规则.采用信号模拟方法获得轴箱轴承的故障信号,利用成熟检测器集合进行故障检测,以验证本文所提方法的有效性和可行性.
1 物元-阴性选择模型
1.1 NSA 原理
NSA 算法的基本思想是通过自体集生成检测器集,并利用检测器对设备进行异常检测.目前检测器主要采用实值表示方法[9],利用高维实值向量构建检测器,以实现问题空间与实值空间的对应.图1所示为利用NSA 算法进行故障检测的基本流程.

图1 NSA 用于故障检测的基本流程Fig.1 Basic process of NSA for fault detection
1.2 物元-阴性选择(M-NSA)算法
物元是可拓学的逻辑细胞,用有序三元数组(N,C,V)表示[7],其中N指代事物,C为事物的特征,V为C的量值.通常采用多维特征对事物N进行描述,形成n维物元MN.

在构建物元-阴性选择模型时,首先进行如下定义:设问题空间U为n维向量(c1,c2,···,cn)所构成的全集;自己空间S为描述设备正常状态下的自体集,S⊂U;非己集合F构成非己空间,为自体集合在U上的补集,表示设备可能发生的各种异常状态,且S∪F=U,S∩F=Ø;检测器为属于非己集合的n维实值向量,且不与自体集匹配.
考虑各特征参数可能存在数量级的差异,为提高计算效率、降低诊断误差,将U表示为由(c1,c2,···,cn)构成的归一化超矩形空间,如式(2).
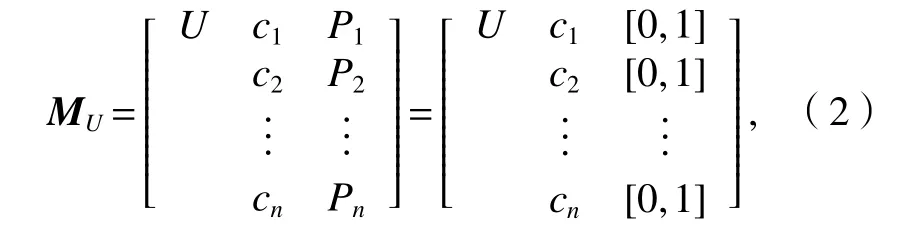
式中:Pi=[0,1](i=1,2,···,n)为第i个特征ci在问题空间U上的区域.
设训练集T={Tk,k=1,2,···,nt}⊂S、检测器集D={Dj,j=1,2,···,nd}⊂F、待测样本集Y={Yu,u=1,2,···,ny}⊂U.分别将Tk、Dj和Yu表示为n维物元形式,如式(3)~(5).
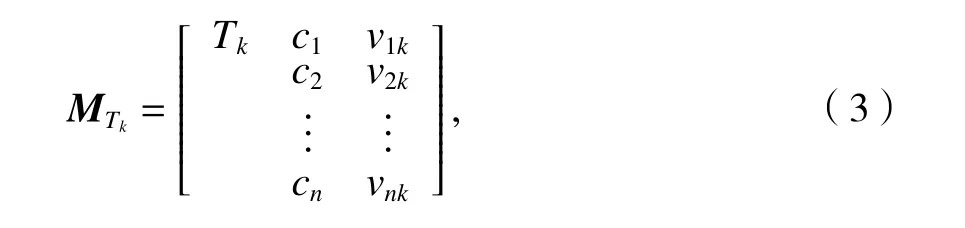

1.3 亲和力计算
匹配规则也称为亲和力计算,用于描述抗体与抗原之间的相似性[9].亲和力不仅用于检测器的生成,还用于待测样本的检测.M-NSA 算法利用关联函数计算亲和力.关联函数以距为基础,设X0=
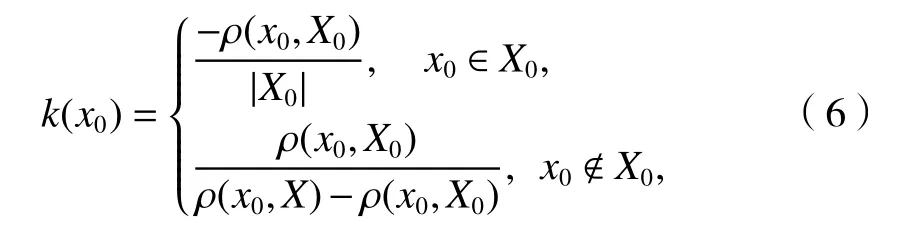
式中:k(x0)的正负和大小表明了x0属于或不属于X0的程度;ρ(x0,X0)和ρ(x0,X)为可拓距离,分别表示x0与X0、x0与X之间的距离,如式(7).
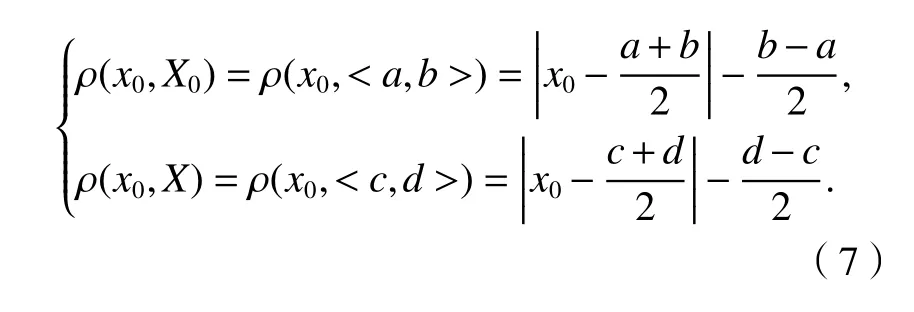
本文利用关联函数进行检测器的生成和待测样本的检测.根据式(2)~(7),训练样本Tk(或待测样本Yu)第i个特征ci的量值vi关于区间Pi和Vij的关联函数为

当0≤k(vi)≤ 0.5 时,vi∈Vij,且k(vi)值越大,vi属于Vij的程度越高;当−1≤k(vi)<0 时,vi∉Vij,即vi不与Vij匹配.因此,可将关联函数作为NSA 的匹配规则,一方面根据检测器与训练样本的匹配程度生成候选检测器;另一方面根据待测样本与检测器的匹配程度进行异常检测.
由于问题空间、检测器、训练样本和待测样本均为n维物元形式,而式(8)仅计算了一维特征的匹配程度,故引入综合关联度将一维亲和度的计算拓展到n维.待测样本物元(或训练样本物元)与检测器物元之间的综合关联度为

2 检测器的生成与优化
如何用较少的检测器实现对非己空间的更大覆盖,降低检测器集合的冗余度是NSA 的关键问题.本文采用PSO 算法生成候选检测器,同时提出合并规则,实现对候选检测器集合的优化.
2.1 PSO 算法
PSO 算法是一种群体智能算法,最早由Kennedy和Eberhart 博士提出.算法通过初始化一群粒子,使粒子在可行解空间中运动,通过追踪个体极值Pbest和群体极值Gbest来更新个体位置.通过比较新粒子的适应度值与个体极值和群体极值的适应度,更新Pbest和Gbest.标准PSO 算法的粒子速度和位置更新公式为[10]
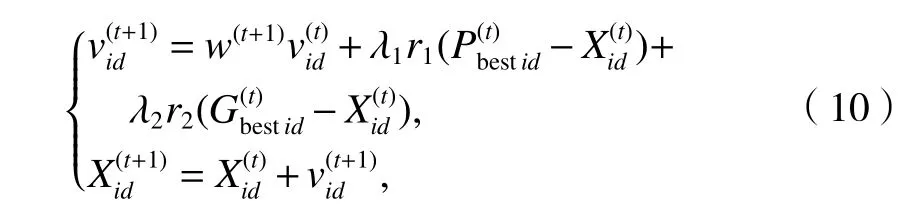
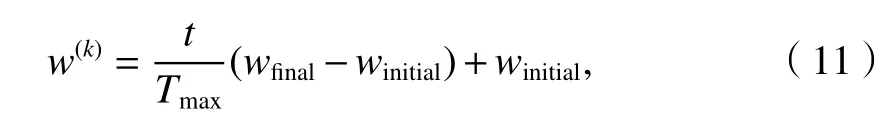
式中:winitial为初始权重;wfinal为最终权重;Tmax为最大迭代次数.
2.2 检测器的生成
利用PSO 算法生成候选检测器时,首先应确定适应度函数.由式(6)~(9)及NSA 意义知:在利用自体集为训练样本生成检测器时,训练样本与检测器之间的综合关联度小于0,且综合关联度越小,训练样本与检测器之间的亲和力越小,检测器属于非己空间的程度越强.因此,本文采用式(12)的适应度函数生成候选检测器.

2.3 检测器的优化
以式(13)为约束条件时,利用PSO 算法可以得到各约束区间内的最优候选检测器,此时候选检测器集可能存在冗余.若两个候选检测器在某一特征取值区间的关联度大于0,则这两个检测器关于该特征的取值区间存在重叠,需要进行优化合并.结合关联函数,制定具体的合并规则:设Dr和Ds(r,s=1,2,···,nd,且r≠s)为两个候选检测器,特征ci在Dr和Ds上的取值区间分别为Vri=[vra,vrb]、Vsi=[vsa,vsb]:


按上述合并规则对整个候选检测器集进行一次计算,得到若干彼此独立的特征参数区间;对这些区间再进行二次合并,进而得到无冗余的成熟检测器集合.
3 轴箱轴承故障检测
3.1 轴承故障检测流程
利用本文所提的M-NSA 方法进行轴承故障检测的基本流程为
步骤1构建物元模型:利用特征提取方法构建问题空间和自己空间,并将其表示为多维物元形式;
步骤2检测器的生成:利用PSO 算法生成候选检测器,首先初始化PSO 算法参数,然后以式(12)和式(13)为优化函数,生成候选检测器集合;
步骤3检测器的优化:根据制定的合并规则对候选检测器集的各维特征取值区间进行合并,得到无冗余的成熟检测器集合;
步骤4故障检测:利用相同的特征提取方法构建待测样本的物元模型,利用成熟检测器进行故障检测.若待测样本与检测器之间的亲和度大于0,则标记为故障;反之,标记为正常.
3.2 特征提取
考虑设备安装的方便性和可操作性,在被测转向架的轴箱正下方布置三向振动加速度传感器,如图2 所示.由于垂向振动信号能更好地表现轴承振动特性,故以垂向振动信号作为分析对象.传感器采用压电式加速度传感器,灵敏度100 mV/g,量程50 g,采样频率2048 Hz.

图2 轴箱轴承传感器布置Fig.2 Axle box bearing sensor arrangement
在进行特征提取之前,需要对采集到的轴承振动信号进行预处理,以最大限度的抑制或消除干扰噪声.本文采用零均值化、剔除奇异点和数据平滑处理的方法进行振动信号的预处理.图3 所示为列车300 km/h 运行时,轴箱轴承6 s 的垂向振动信号,图4为经过预处理后的振动信号.
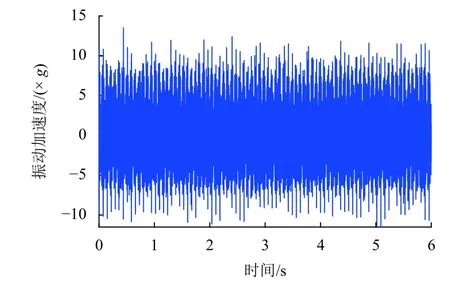
图3 轴箱轴承垂向振动信号Fig.3 Vertical vibration signal of axle box bearing
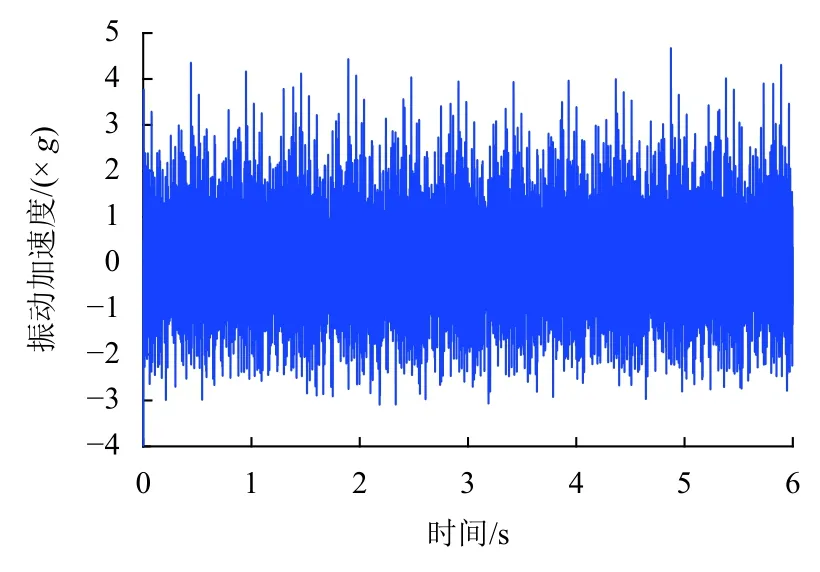
图4 预处理后的轴承振动信号Fig.4 Vibration signal of axle box bearing after preprocessing
小波变换在时、频两域均具有较强的信号局部特征表征能力[11],适用于非平稳、非线性信号的处理;且小波能量反应了信号在小波变换各频带内的能量分布信息,同时因问题空间U为归一化的超矩形空间,故本文以归一化的各频带小波能量构建特征向量.采用db3 小波对轴承振动信号进行4 层小波分解,得到归一化的小波能量,利用向量形式表示为E=(E1,E2,E3,E4,E5).为构建自己集合,在振动信号中选取100 组数据,每组2048 点,用db3 小波进行4 层小波分解.表1 为各频带的分布,图5 为100 组训练样本在各频带的归一化小波能量分布.

表1 各频带的频率范围Tab.1 Frequency range of each frequency band Hz
3.3 检测器的生成与优化
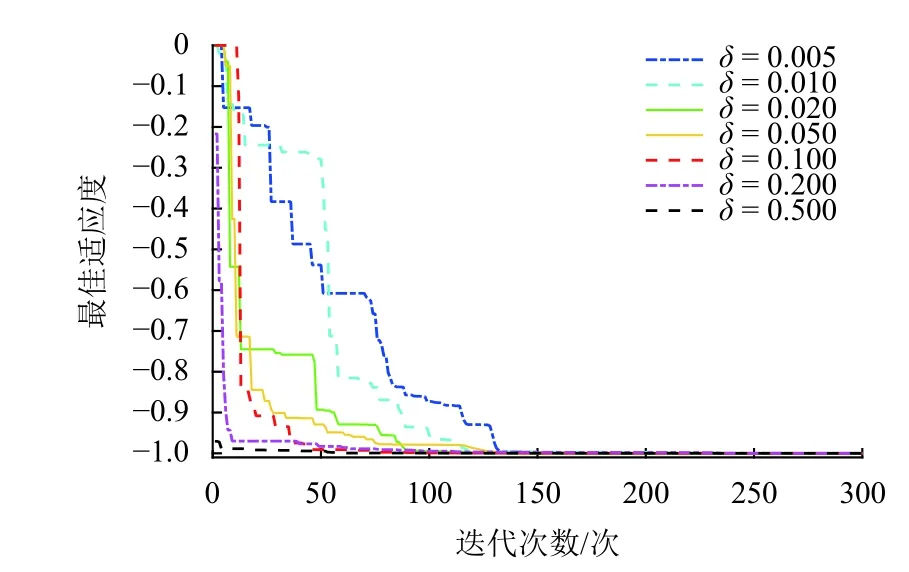
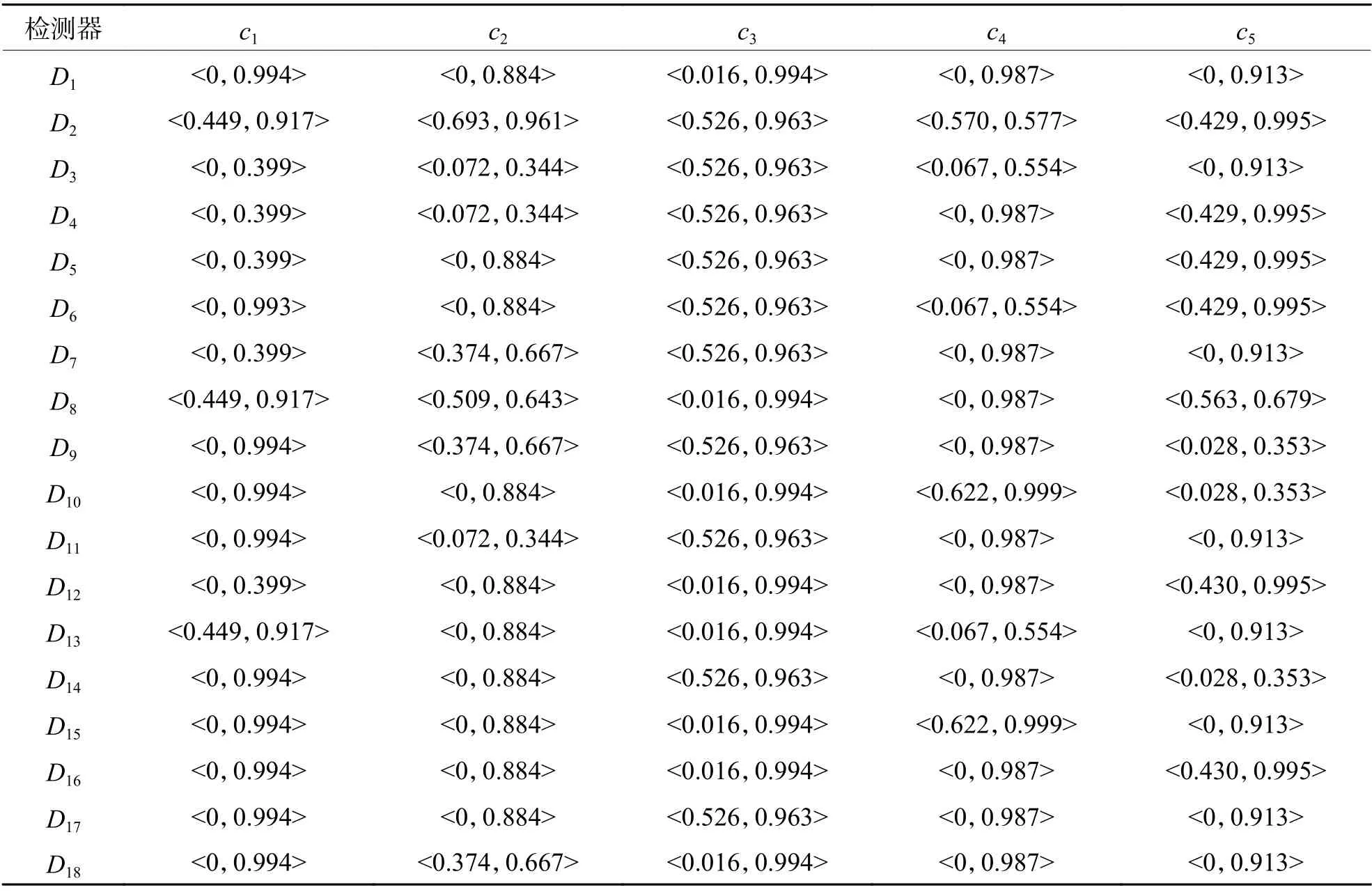
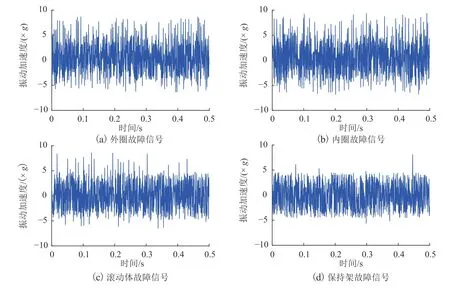
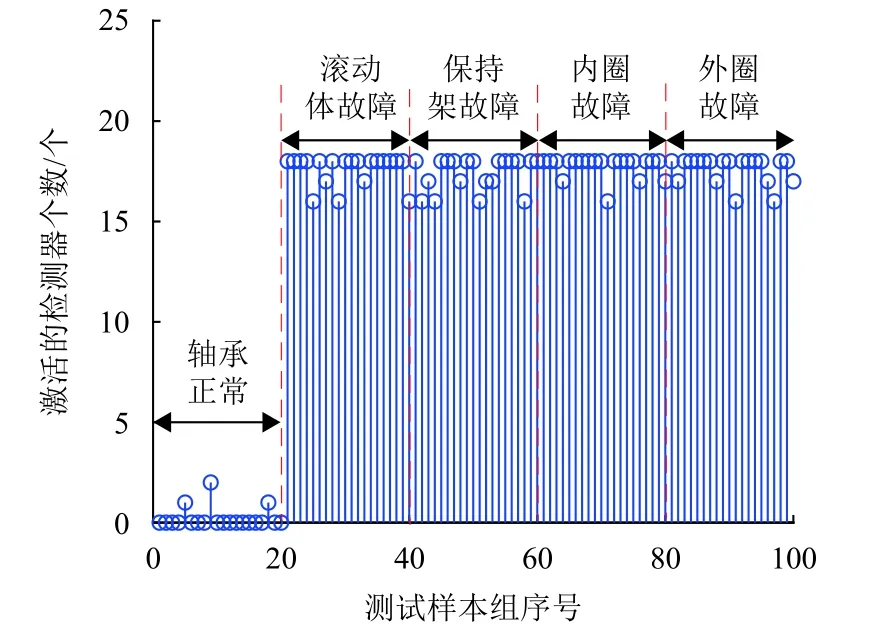
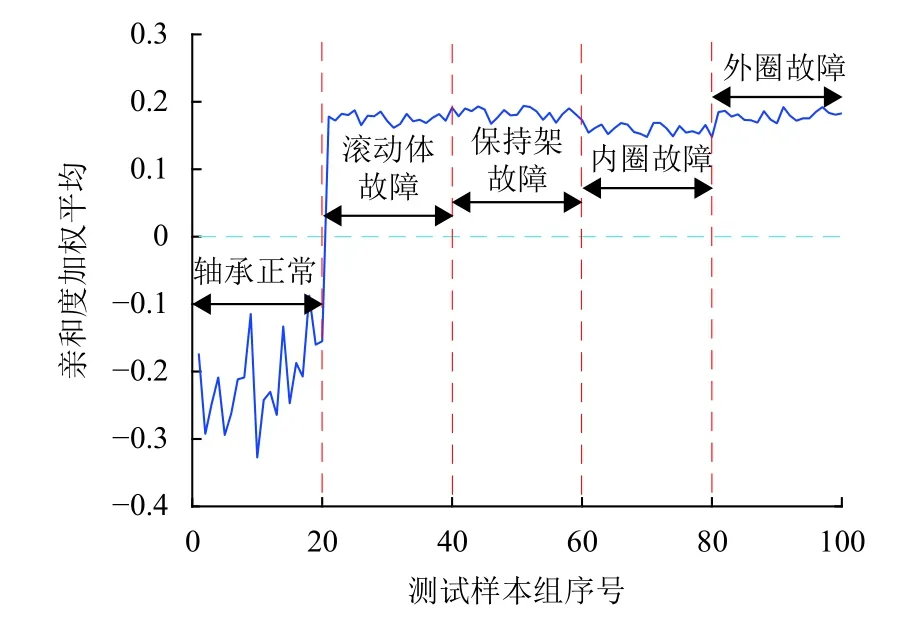
对PSO 算法进行参数初始化,种群规模为20,加速因子λ1=λ2=1.49445,终止阈值ε=1×10−9,Tmax=300,粒子维数=10,粒子运动空间为[0,1].按式(11)更新惯性权重,winitial=0.9,wfinal=0.4.为降低粒子在进化过程中离开搜索空间的几率,限定粒子最大速度为空间范围的20%.为保证迭代过程中vl,ij 设式(12)中各频带的归一化小波能量权重相等,即ωi=0.2(i=1,2,···,5).在自体集中随机选取80 组数据作为训练样本,生成候选检测器.图6所示为δ=0.1 时的寻优过程. 图6 适应度曲线(δ=0.100)Fig.6 Fitness curves(δ=0.100) 由式(13)知,δ直接影响PSO 算法的收敛速度及检测器的有效生成.δ取值不同时,得到的最佳适应度值也不同.为便于比较,取适应度在[−0.1,0]区间时,不同δ下的最佳适应度变化曲线,如图7 所示. 由图7 知:δ越小,对适应度区间的划分越细,PSO 算法的收敛速度越慢,且收敛速度随δ的增大而提高;δ过大(如δ=0.500)会导致对适应度区间的划分粗糙,造成检测器无法有效覆盖非己空间;式(9)中,综合关联度趋于0,表明检测器靠近自己空间.因此,为避免“黑洞”的产生,对综合关联度趋于零的区间应进行细分;为提高收敛速度,对综合关联度趋于−1 的区间进行粗分.综上,采用不同的控制参数划分[−1,0]区间:当 −0.2≤K(,MD)≤0时,取δ=0.005;当 − 1.0≤K(,MD)<−0.2时,取δ=0.020,由此生成80 个候选检测器.利用前文所述规则对候选检测器进行优化,得到18 个成熟检测器,如表2 所示. 图7 不同控制参数下的适应度曲线Fig.7 The fitness curves with different control parameters 表2 成熟检测器分布Tab.2 Mature detector distribution 由于轴箱轴承在信号采集阶段始终处于正常运行状态,故利用信号模拟方法获得轴箱轴承的故障信号.试验用高速列车轴箱轴承具体参数及故障特征频率见表3.利用文献[12]所提方法得到轴箱轴承的各类故障信号,如图8. 表3 轴箱轴承基本参数Tab.3 Basic parameters of axle box bearing 图8 轴承故障信号Fig.8 Bearing fault signals 在获得滚动轴承故障信号后,利用前文特征提取方法进行特征提取,构建待测样本.为验证本文所提方法的有效性,选取20 组正常数据和80 组故障数据(每类故障取20 组数据)进行轴箱轴承的故障检测.若待测样本与检测器之间的综合关联度大于零,则检测器被激活.图9 为待测样本所激活的检测器个数,图10 为待测样本与18 个成熟检测器之间的亲和度加权平均值. 图9 激活的检测器个数Fig.9 Number of the activated detectors 图10 待测样本与检测器之间的亲和度Fig.10 Weighted affinity between the tested samples and detectors 由图10 知:20 组轴箱轴承正常状态样本与成熟检测器之间的亲和度均值为−0.2127;4 类故障样本与成熟检测器之间的亲和度均值分别为0.1763、0.1827、0.1587 和0.1797,表明生成的成熟检测器对不同类轴承故障均具有较好的敏感性. 定义检测器激活率为激活的检测器个数与检测器总数之比,根据图9 得到轴承在各类运行状态下的检测器激活率,见表4. 表4 检测器激活率Tab.4 Detector activation rate % 由表4 知:轴承正常运行状态样本激活的检测器较少,而故障样本几乎激活全部检测器;且在轴承不同故障类别下,检测器激活率的最大偏差为1.94%,生成的检测器对不同类轴承故障均具有较高的检测性能;部分检测器存在误判,主要是因检测器的特征参数区间与对应的自己空间存在部分重合,可通过对非己空间的进一步细分得以提高. 本文针对轴箱轴承故障数据获取困难的问题,结合NSA 算法和物元模型各自的特点,提出了无需先验知识的轴箱轴承故障检测方法: 1)在检测器生成阶段,以检测器与训练样本之间的综合关联度作为匹配规则构建适应度函数,利用PSO 算法寻优生成候选检测器,并分析了控制参数对检测器生成及PSO 算法收敛速度的影响; 2)在检测器优化阶段,以特征参数在两个检测器对应区间的关联度作为判决条件,制定了检测器的合并规则,并对候选检测器集进行优化,将检测器个数由80 个降低至18 个; 3)采用信号模拟方法获得轴箱轴承的各类故障信号并构建故障状态的待测样本,利用成熟检测器集合进行检测.结果表明,正常样本与成熟检测器之间的亲和度均值为−0.2127,故障样本与成熟检测器之间的亲和度不小于0.1587;正常样本的检测器激活率为1.11%,故障样本的检测器激活率不低于96.67%.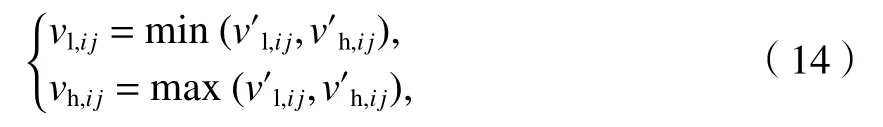

3.4 轴箱轴承故障检测


4 结 论
