温梯荷载下桥上CRTS Ⅱ型板式无砟轨道的力学特性
2021-10-31张鹏飞雷晓燕刘林芽
张鹏飞,涂 建,桂 昊,雷晓燕,刘林芽
(1.华东交通大学铁路环境振动与噪声教育部工程研究中心,江西 南昌 330013;2.华东交通大学土木工程国家实验教学示范中心,江西 南昌 330013)
无砟轨道因其具有高平顺性、高可靠性和少维修性等诸多优点,已成为高速铁路的主要轨道结构型式之一.其中,CRTS Ⅱ型板式无砟轨道在京沪、沪昆高铁,京津城际等线路上大量铺设[1],长期暴露在环境中的无砟轨道结构不仅承受列车荷载,而且还承受环境变化引起的温度荷载[2].由于桥上轨道板和底座板为纵向连续的结构,使其对温度作用较为敏感,可能导致轨道结构翘曲变形、层间分离及滑动层破损等危害[3],影响轨道结构受力性能和耐久性.
目前,国内外学者对无砟轨道结构温度荷载模式和温度荷载作用下,桥上无砟轨道无缝线路纵向受力特性展开了一定程度的研究.刘学毅等[4]和欧祖敏等[5]针对无砟轨道温度场变化问题,对某高速铁路无砟轨道结构温度场展开了现场监测试验,通过建立无砟轨道温度简便计算方法得出了其竖向温度梯度荷载模式;曾志平等[6-7]建立无砟轨道温度场有限元模型,并结合现场实验数据研究了不同线路方向和地理纬度对无砟轨道温度梯度的影响规律,发现无砟轨道侧表面法向与正南向夹角为90° 时,无砟轨道的垂直和水平温度梯度处于最不利的状态,且高纬度地区比低纬度地区影响更大;曲村、蔡小培等[8-10]分析了温度荷载作用下桥上CRTSⅠ型、CRTSⅡ型板式无砟轨道及双块式无砟轨道无缝线路纵向力分布规律及其影响因素,发现采用桥上“两布一膜”滑动层结构后的纵连板式无砟轨道无缝线路,钢轨纵向附加力比一般桥上无缝线路小很多[9];谢铠泽等[11]分析了在轨温变化时不同控制指标下墩顶水平位移、线路纵向坡度、桥梁伸缩对桥上单元板式无砟轨道温度跨度限值的影响;闫斌等[12-13]建立了某大跨斜拉桥塔-索-轨-梁-墩-桩空间有限元模型,研究了斜拉桥上无缝线路纵向力传递规律,并指出计算斜拉桥上无缝线路纵向力需要考虑相邻桥梁的影响;戴公连等[14-16]分析了小阻力和常阻力扣件对大跨度连续梁桥上附加纵向力的影响,结果表明采用小阻力扣件时桥梁墩台受力和钢轨伸缩附加力均可减小40%~50%,并基于实测数据利用统计方法得到桥梁的非线性温度模式,分析了在实测非线性温度模式下桥上纵连板式无砟轨道纵向力的分布规律.纵观上述已有的研究成果,主要是对不同线路环境下无砟轨道温度梯度分布规律,年温差荷载作用下不同桥式桥上无缝线路纵向力及其相关影响因素的研究,关于温度梯度荷载对桥上无缝线路纵向受力的影响研究鲜有报道.
基于以往的研究,本文基于梁-板-轨相互作用原理和有限元法,建立了高速铁路大跨度连续梁桥上CRTSⅡ型板式无砟轨道无缝线路空间精细化有限元模型,研究桥上无砟轨道在轨道板竖向温度梯度和阴阳面横向温度梯度作用下无缝线路纵向力和位移分布规律,研究成果可为高温差地区东西走向的桥上CRTSⅡ型板式无砟轨道无缝线路的设计及运营维护提供理论指导和技术参考.
1 模型建立
1.1 模型主要组成
高速铁路大跨度桥上 CRTSⅡ型板式无砟轨道无缝线路空间精细化有限元模型中主要包括钢轨、扣件、轨道板、砂浆层、底座板、滑动层、固结机构、桥梁、过渡板、摩擦板、端刺、路基等结构.本文以3×32 m 简支梁+(70+130+70) m 连续梁+3×32 m 简支梁双线桥为例说明建模过程.
1.2 模型参数
1.2.1 钢轨、扣件
钢轨为CHN60 标准钢轨,采用基于Timoshinko梁理论的Beam188 梁单元模拟;路基和桥上扣件均采用WJ-7 型常阻力扣件,扣件间距为0.65 m,采用线性弹簧-阻尼器单元模拟扣件的横向和垂向刚度,扣件横向和垂向刚度分别为50 kN/mm 和35 kN/mm;扣件对钢轨的纵向约束采用非线性弹簧单元模拟,为便于桥上无缝线路的计算,WJ-7 型常阻力扣件的纵向阻力采用双线性阻力模型,其阻力-位移曲线如图1 所示,伸缩力扣件纵向阻力(15 kN/组)按无载时扣件阻力-位移曲线取值.
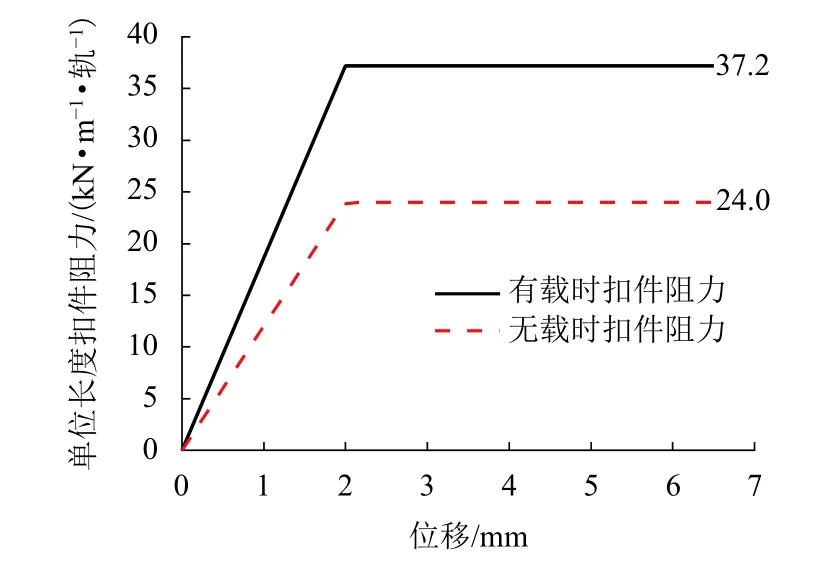
图1 WJ-7 常阻力扣件阻力-位移曲线Fig.1 Resistance-displacement curves of WJ-7 ordinary resistance fastener
1.2.2 Ⅱ型板式无砟轨道结构
简支梁、连续梁和路基段均采用标准轨道板,轨道板厚0.20 m、长6.45 m、宽2.55 m,为C55 预应力混凝土结构;CA(cement asphalt)砂浆厚0.03 m、宽2.55 m,桥上与路基纵连,弹性模量为7000 MPa.底座板厚0.19 m、宽2.95 m,为纵向连续的C30 混凝土结构;采用实体单元模拟轨道板、CA 砂浆层和底座板.
1.2.3 桥梁和路基
桥梁、过渡板、摩擦板、端刺、路基截面结构参数均按实际工程设计参数及尺寸进行建模,采用实体单元模拟.变截面连续箱梁和等截面简支箱梁均为C55 预应力混凝土结构,摩擦板、端刺、路基为C30 混凝土结构,简支梁截面如图2.

图2 简支箱梁截面Fig.2 Cross-section of simply supported bridge
1.2.4 其它结构参数
采用线性弹簧-阻尼器单元模拟桥梁墩/台固定支座及其上方固结机构的纵向约束,其中,简支梁固定支座桥墩、连续梁固定支座桥墩、固定支座桥台、固结机构的纵向刚度分别取400、2000[17]、3000、10000 MN/m.底座板与梁体、底座板与摩擦板之间都采用非线性弹簧连接,分别模拟桥上“两布一膜”滑动层和摩擦板上滑动层的纵向阻力,其滑动层摩擦系数分别取0.30 和0.70.
1.3 空间精细化有限元模型
高速铁路大跨度连续梁桥上CRTSⅡ型板式无砟轨道无缝线路空间精细化有限元模型主要由以上各结构组成,模型如图3 所示.其中,桥上无缝线路两端分别设置150 m 的路基段,以消除模型边界效应;本模型根据各轨道及桥梁结构的细部尺寸及温度梯度荷载施加精度要求进行网格划分,保证各轨道和桥梁单元网格划分细致整齐以及保证模型计算结果的精确性.
图3 空间精细化有限元模型Fig.3 Refined spatial finite element model
1.4 模型验证
本文采用上述方法建立了与文献[17]相同结构尺寸及力学参数的有限元模型,对梁体整体降温30 ℃,桥上无砟轨道整体降温45 ℃,计算出钢轨伸缩力和钢轨纵向位移最大值分别为40.304 kN、1.76 mm;在相同温度荷载工况条件下,文献[17]中钢轨伸缩力和钢轨纵向位移最大值分别为41.066 kN、1.76 mm.如图4 所示,本文钢轨纵向力分布规律与文献[17]基本一致,且计算结果比较吻合,验证了本文所建模型的准确性和可靠性.
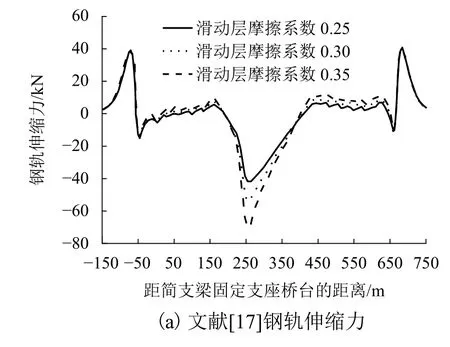

图4 钢轨伸缩力Fig.4 Expansion-contraction force of rails
2 轨道板竖向温度梯度的影响
在实际情况中,无砟轨道结构受太阳辐射时,由于混凝土的导热系数较低[18]及周围环境的影响,使得轨道结构温度分布受其厚度的影响较大,在距轨道板表面0~0.20 m 内非常明显[19],且近似呈线性温度梯度变化[6].因此,本节主要分析轨道板竖向温度梯度对桥上无砟轨道无缝线路纵向力和位移的影响,根据高速铁路设计规范(TB 10621—2014)[20]轨道板竖向温度梯度设置3 种工况,分别为 50、70 ℃/m和90 ℃/m(正温度梯度),轨道板的板面温度取50 ℃,CA 砂浆、底座板和桥梁梁体的温度荷载分别取35、35、30 ℃.
轨道板竖向温度梯度作用下,各轨道与桥梁结构纵向应力和位移最大值计算结果分别见表1 和表2,其中:正值和负值分别代表轨道及桥梁结构的拉伸和压缩变形,即拉(应)力和压(应)力;Fr和Dr分别为钢轨最大伸缩力和位移;Stsu和Stsl分别为轨道板上表面和下表面纵向应力最大值;Δts为轨道板上表面和下表面纵向应力差最大值;Sbpu和Sbpl分别为底座板上表面和下表面纵向应力最大值;Δbp为底座板上表面和下表面纵向应力差最大值;Fa和Da分别为简支梁固定支座桥台纵向力最大值和位移最大值;Fp和Dp分别为固定支座桥墩纵向力最大值和位移最大值;Dtsu为轨道板上表面纵向位移最大值;Δrts为轨板相对位移最大值;Dbpl为底座板下表面纵向位移最大值;Δbpb为底座板桥梁相对位移最大值;Db为桥梁位移最大值.
由表1 和表2 可知:在其他温度荷载相同的情况下,轨道板竖向温度梯度对钢轨的纵向力影响不大;竖向温度梯度越大,轨道板上表面与下表面应力差也越大,在轨道板竖向温度梯度从50 ℃/m 增至90 ℃/m 时,轨道板上表面与下表面应力差最大值增大了25.6%;钢轨附加力主要由桥梁的伸缩变形产生,钢轨的纵向附加力最大值只增大了0.013 kN,变化不明显,钢轨纵向位移峰值均为1.60 mm,没有变化.由于桥上采用滑动层结构,大大削弱了桥梁伸缩对轨道结构的受力影响,轨板相对位移最大值仅为0.24 mm,底座板和桥梁的相对位移最大值为57.19 mm.同理,轨道板竖向温度梯度产生的纵向应力通过层间摩擦阻力和固结机构,向下传递时经过滑动层的削减,使得桥梁及其墩台的纵向受力与变形不受影响.

表1 竖向温度梯度作用下结构纵向力最大值Tab.1 Maximum longitudinal forces of structure under vertical temperature gradient

表2 竖向温度梯度下结构纵向位移最大值Tab.2 Maximum longitudinal displacements of structure under vertical temperature gradient mm
因此,竖向温度梯度的存在会使轨道板出现翘曲应力,甚至产生翘曲变形而导致轨道结构病害,在高温差和温度易出现急剧变化的地区应该对轨道板进行特殊配筋设计,防止轨道板出现较大的翘曲变形而影响线路稳定和列车运行安全.
3 横向温度梯度的影响
无砟轨道温度场的分布不仅受气温、风速、日照辐射强度等环境因素的影响,还与线路走向有密切关系[7],对于东西向线路,在太阳辐射下线路两侧一侧处于向阳侧,另一侧处于背阴侧,向阳侧的桥梁和无砟轨道结构温度高于背阴侧,即这种现象被定义为阴阳面[21].如图2 所示,背阴侧与向阳侧以线路中心线为界限,线路中心线左侧为向阳侧,线路中心线右侧为背阴侧,当线路出现阴阳面时,左线桥梁及轨道结构对右线产生遮挡作用,线路两侧桥梁与轨道结构会产生横向温度差.本节中,轨道板竖向温度梯度取50 ℃/m,设计了2 种阴阳面横向温度荷载工况和一个无温度差工况进行对比,阴阳面桥梁与各轨道结构温度荷载根据《铁路无缝线路设计规范》(TB 10015—2012)[22]中的相关规定取值,详见表3.
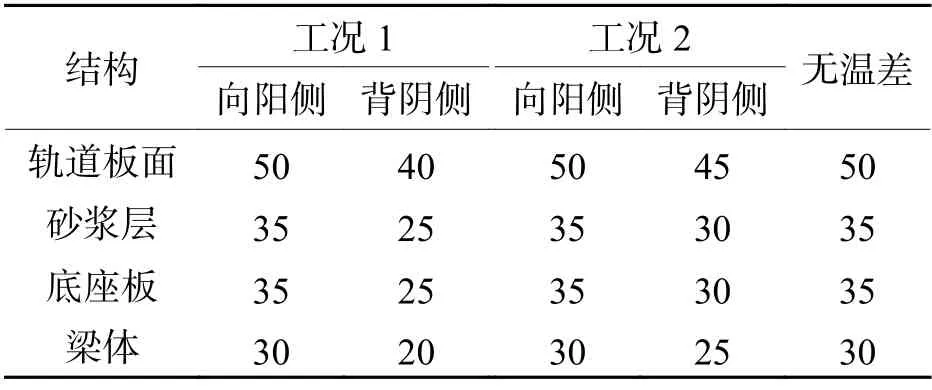
表3 阴阳面横向温度梯度荷载工况Tab.3 Transverse temperature gradient load condition of southern and northern surfaces ℃
阴阳面横向温度梯度荷载条件下钢轨伸缩力和位移、轨道板上表面和下表面应力、底座板上表面和下表面应力、固定支座墩台顶纵向力和位移如图5~8 所示,各轨道与桥梁结构最大纵向力和纵向位移计算结果分别见表4 和表5.

表4 横向温度梯度荷载下结构纵向力最大值Tab.4 Maximum longitudinal forces of structure under transverse temperature gradient load

表5 横向温度梯度荷载下结构纵向位移最大值Tab.5 Maximum longitudinal displacements of structure under transverse temperature gradient load mm
由图5~8、表4、5 可知:在阴阳面横向温度梯度荷载作用下,向阳侧的轨道板应力和底座板应力均高于背阴侧;阴阳面横向温度梯度越大,阴阳面两侧轨道板应力差和底座板应力差值越大,向阳侧和背阴侧桥墩最大纵向力差值及连续梁上向阳侧和背阴侧钢轨最大纵向力差值也越大.以工况1 为例,背阴侧连续梁桥墩固定支座纵向力是向阳侧的3.5 倍,背阴侧钢轨最大的纵向力是向阳侧的1.4 倍.
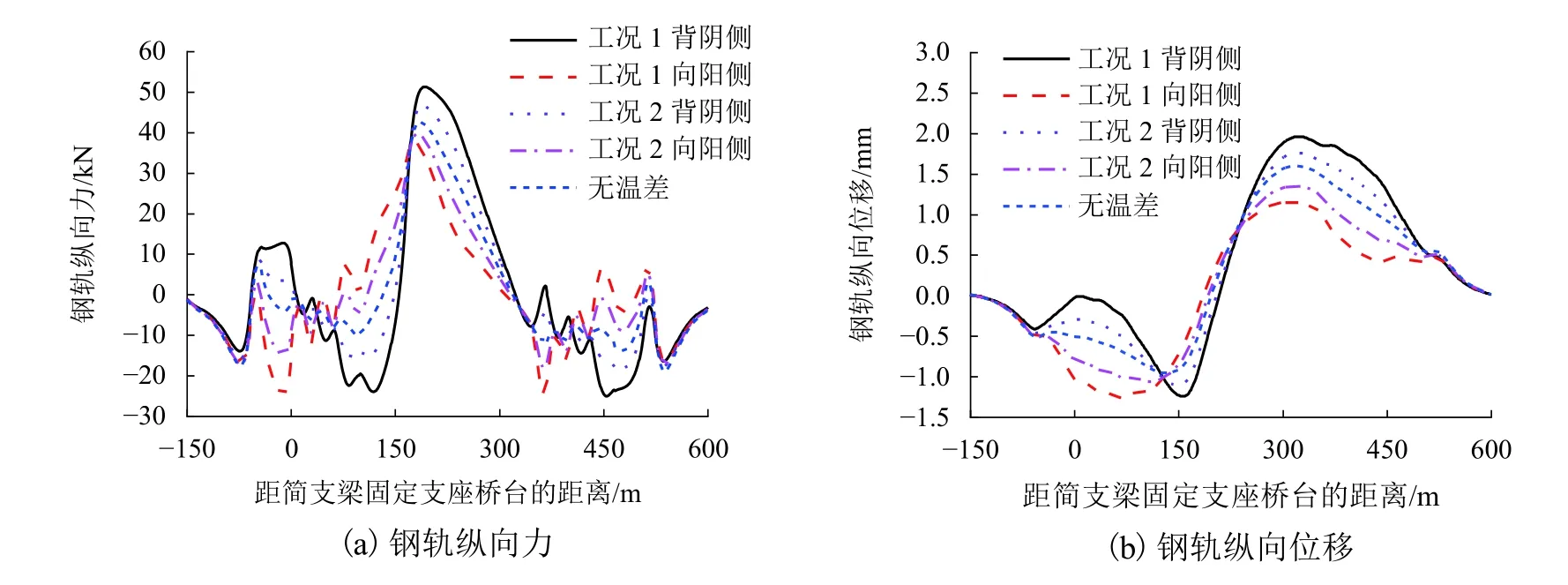
图5 不同工况钢轨纵向力和位移Fig.5 Longitudinal force and displacement of rails under different conditions
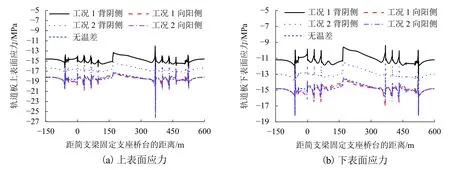
图6 不同工况轨道板上、下表面应力Fig.6 Upper and lower surface stress of track slab under different conditions

图7 不同工况底座板上、下表面应力Fig.7 Upper and lower surface stress of bed plate under different conditions
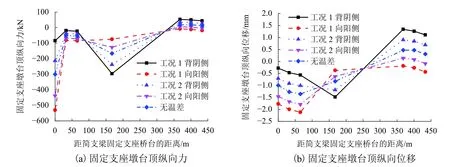
图8 不同工况固定支座墩台顶纵向力和位移Fig.8 Longitudinal displacement of fixed pier and abutment top under different conditions
简支梁和连续梁梁体均仅在支座处有横向约束,因此,在阴阳面横向温度梯度荷载作用下梁体及桥上无砟轨道不仅会发生纵向伸缩变形,还会发生横向扭曲变形,工况1 条件下轨道和桥梁结构变形如图9 所示.桥梁的纵向伸缩和横向弯曲变形均会对桥上无缝线路钢轨产生纵向附加力,简支梁背阴侧梁体内凹、向阳侧梁体外凸,由于简支梁梁体跨度较小,在阴阳面横向温度梯度作用下梁体横向扭曲变形较小,钢轨附加力主要来自梁体纵向伸缩变形.连续梁由于主桥梁体的连续性使得连续梁主跨与边跨的变化趋势相反,其中边跨向阳侧梁体外凸、背阴侧梁体内凹,主跨向阳侧梁体内凹、背阴侧梁体外凸.桥梁梁体外凸会使钢轨纵向位移变大,从而增加钢轨附加纵向力,梁体内凹使钢轨纵向位移减小,从而减小钢轨附加纵向力.阴阳面横向温度梯度越大,桥梁梁体横向扭曲变形越大,对钢轨附加纵向力和位移的影响越大,在阴阳面横向温度差为5 ℃和10 ℃下,背阴侧钢轨附加力最大值比向阳侧分别大17.5%和36.0%,背阴侧钢轨纵向位移最大值比向阳侧分别大29.4%和69.0%.
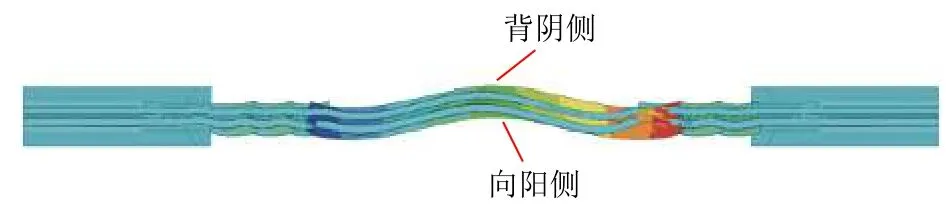
图9 轨道和桥梁结构变形Fig.9 Deformation diagram of track and bridge structure
在横向温度梯度作用下,墩台顶纵向力变化明显,横向温度梯度越大,背阴侧的连续梁固定支座墩顶纵向力和位移越大,向阳侧的连续梁固定支座墩顶纵向力和位移越小;靠近桥台一侧的简支梁固定支座,由于桥梁的温度跨度小,桥梁扭曲变形较小,向阳侧墩台顶纵向位移比背阴侧的大,远离桥台一侧的简支梁固定支座,由于桥梁的温度跨度大,受连续梁横向扭曲变形的影响较大,使得背阴侧墩台顶纵向位移比向阳侧的大.
4 结 论
1)轨道板竖向温度梯度对钢轨、底座板、桥梁及墩台顶的纵向受力与变形几乎没有影响,只对轨道板的纵向受力有影响.轨道板竖向温度梯度越大,轨道板上表面和下表面应力差也越大.
2)横向温度梯度对线路两侧轨道和桥梁结构纵向受力与位移影响较大,当阴阳面横向温度差为10 ℃时,连续梁上背阴侧钢轨最大的纵向力是向阳侧的1.4 倍,背阴侧桥墩最大的纵向力是向阳侧的3.5 倍;随着横向温度梯度的增大,背阴侧钢轨纵向力、位移最大值逐渐增大,向阳侧钢轨纵向力、位移最大值逐渐减小.
3)在横向温度梯度荷载作用下,钢轨纵向力由梁体伸缩和扭曲变形共同作用产生;在连续梁桥跨度一定时,横向温度梯度越大梁体的扭曲变形越大,阴阳面两侧钢轨纵向力、位移峰值差越大.
4)在温度易出现急剧变化的地区,设计东西走向的大跨度桥上无缝线路时,需要重点关注轨道板的受力,背阴侧桥梁墩顶纵向力和钢轨纵向力,并对无缝线路的横向稳定性进行检算.
