城市轨道交通故障下客流分布计算及评估方法

2021-10-31刘峰博周庭梁王小敏

西南交通大学学报 2021年5期

刘峰博，周庭梁，王小敏

（1.西南交通大学信息科学与技术学院，四川成都 611756；2.卡斯柯信号有限公司，上海 200071）

作为庞大的复杂系统，城市轨道交通运营受到各类因素影响，故障难以避免且随机发生，引起的列车运行延误或中断影响乘客出行.随着轨道交通路网规模扩大和客流量显著增长，突发运营故障对乘客出行的影响越来越大，但实时预测难度大，客流受影响范围和程度尚缺乏有效的量化方法.

国外学者较多探讨延误影响线间列车衔接及乘客换乘问题[1-2].国内研究除了刻画突发事件下的乘客路径决策行为[3]，较多关注客流量的变化，区分延误客流、绕行客流和损失客流，分别给出其计算方法[4-5]；对比故障和正常情况下的客流数据，得出故障下断面客流呈现先减小后增加再趋于稳定的趋势[6].然而，事后的数据结果难以还原故障情况下运能和客流的动态变化.

目前网络OD（origin-destination）客流难以实时地清分为线路OD 客流，且故障信息的及时推送还未普及.但是，大部分通勤乘客按照习惯出行，故障开始时段客流量与常态相差不大，可根据常态客流的周期性变化规律得到故障开始时各个时空范围的标准客流量[6].基于此，本文探讨故障下客流分布计算和评估方法，通过构建客流与列车交互过程模型及仿真，刻画客流随列车运行变化的时空分布；通过分析列车内和站台上的客流分布指标及不同条件下的乘客出行时间变化，量化评估故障对乘客出行的影响程度，以期为实施客流管控和行车调整措施提供决策依据.

1 客流与列车交互过程建模及仿真

1.1 定义与假设

乘客的动态分布依托于所乘列车的运行状态，如图1 所示，图中不同颜色代表不同车.一个列车或乘客的活动由两个相邻的到发事件组成.实际故障下列车到发事件集合设为 E，其中出发事件集合为Ede.一个列车出发事件设为e∈Ede，全部乘客集合设为G，一个乘客组g∈G为具有相同起始站、终到站和进站时间tg且数量为ng的乘客群，g=将乘客组作为列车运行事件-活动关系的负载，乘客与列车的交互发生在等车、上车和下车3 个过程，可基于对应事件计算等待人数、离开人数、上车人数、留乘人数、车内人数和下车人数等客流分布指标.

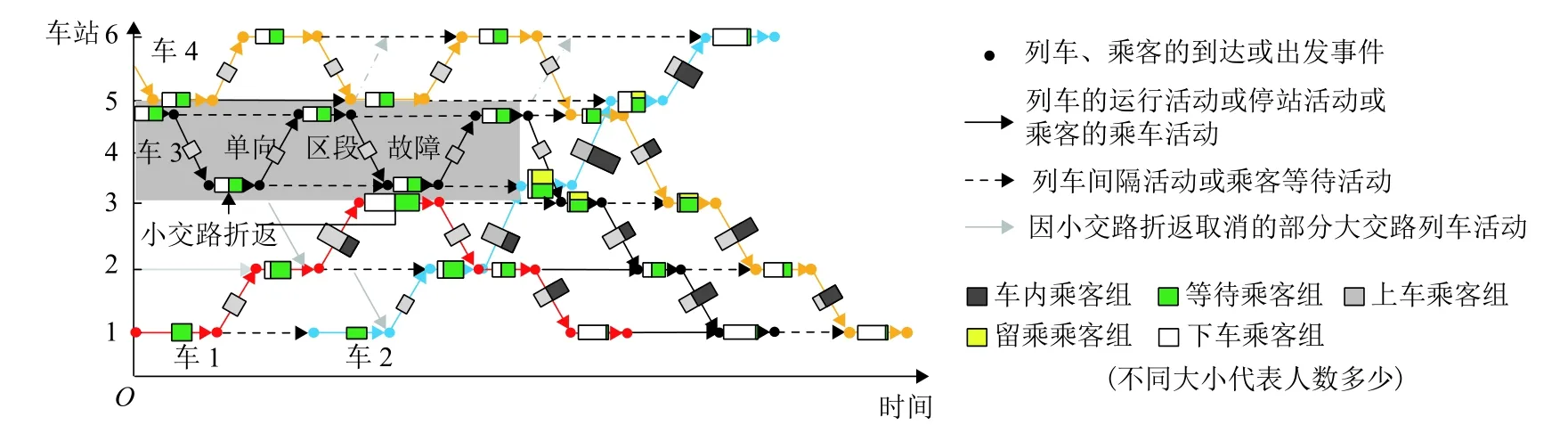
图1 客流与列车交互的事件-活动关系Fig.1 Event-activity relationship of interaction process between passenger flows and trains

为了方便描述和处理模型，给出如下假设：

假设1故障刚发生时到达客流量无明显变化，乘客能够获知下一列车的到站时刻；

假设2乘客不会无限期地等待列车，当得知等待时间将超过一定阈值（设为d），乘客则离开当前线路，选择其他线路或交通方式；

假设3不同目的地的乘客充分混合，且服从先到先服务原则，列车能力不足以容纳同一时刻到达的多个乘客组时，每个乘客组等比例上车，其他乘客则留乘等待下一列车.

1.2 交互过程模型

1）等车过程

考虑到达等待、留乘等待和小交路折返提前下车等待后续长交路列车3 种等车情况，令早于事件e的同向同车站出发事件集合为，根据其是否为空判断是否存在留乘客流.将长交路列车在小交路折返站继续前行的出发事件标记为el∈Ede，与其他出发事件e进行区分.事件e可能对应单个或多个等车情况，不同条件下的等待乘客集合和离开乘客集合分别如式（1）、（2）所示.

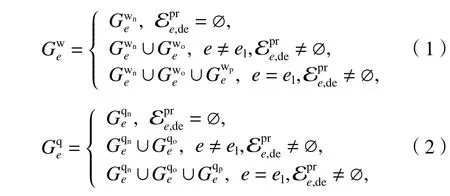
列车剩余能力与事件e是否有同车次上一站出发事件ev、列车能力C、上一站车内人数和本站下车人数有关.将乘客进出站位置作为已知条件，ev发生时将要下车的人数可以计算得到.以事件e为例，车内人数为

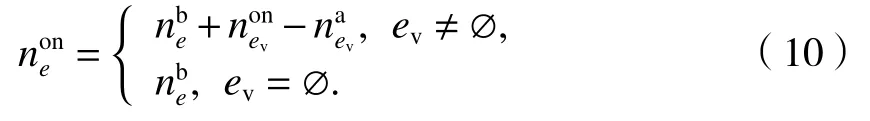
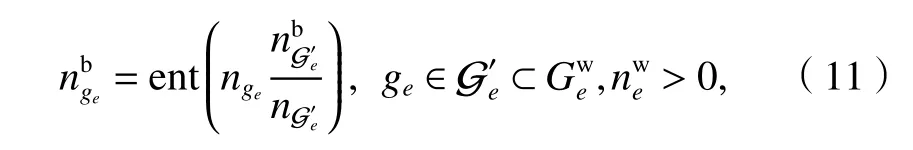
留乘人数为

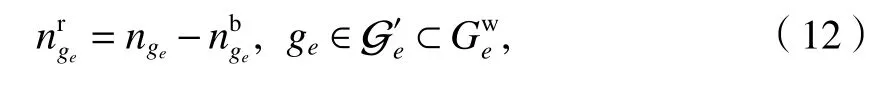
则该分组的上车乘客集合和留乘乘客集合分别为

因此事件e总上车乘客集合由前续全部分组的乘客和该分组部分上车乘客组成，即

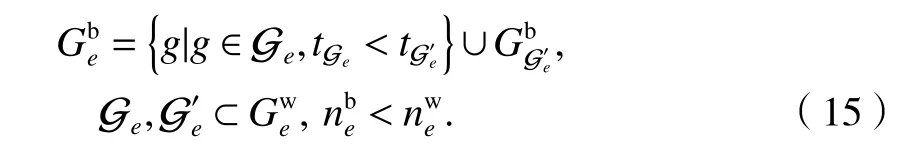
由此，事件e发生时车内乘客集合为

式中：e1,v为小交路折返前一站的出发事件；Ede为当天计划的列车出发事件集合.

1.3 动态客流仿真算法

为了实现上述模型和计算客流分布指标，设计客流与列车交互过程动态仿真算法.

2 乘客服务水平评估指标

在仿真计算客流分布的基础上，进一步分析评估乘客服务水平，包括以下5 个方面的指标：

1）列车满载率

每列车的满载率反映乘客拥挤度，一段时空范围内多列车的满载率可作为运营组织策略调整的依据.通过每个出发事件对应的车内乘客集合可知每个时空位置的车内人数，结合列车定员能力计算每列车的满载率.

2）站台拥挤情况

故障情况下，站台容量饱和、留乘现象普遍存在.多次留乘降低乘客满意度，站台拥挤带来安全隐患.分析留乘乘客和等待乘客的分布和演变特征，关注最大等待人数、最大留乘人数、留乘发生率（发生留乘的车站占比）等，有助于决策是否需要采取缓解措施.

3）乘客离开情况

故障情况下运输能力下降，一部分乘客将因得不到及时服务而离开当前线路，严重时需要公交等方式联动运输.分析离开乘客的数量和分布特征，能查验列车服务与客流需求的总体适应情况，并为公交应急联动等配合方案的制定提供参考.

4）乘客等待时间

包括乘客进站等车时间和在小交路折返站提前下车后等待下一班长交路列车的时间.后者是临时调整情况下增加的等待时间，对其乘以大于1 的惩罚系数 δ.两种条件下，乘客都可能因等待时间过长而离开当前线路，离开前的等待时间不可忽略.每个e对应的乘客等待时间Te,w如式（19）所示，所有事件对应的等待时间合计为总的乘客等待时间.

5）乘客旅行时间

研究时域内所有乘客从各自起始站到终到站的旅行时间，包括等待时间和乘车时间.其中等待时间见式（19），乘车时间的计算同样考虑得到服务和离开两种情况.考虑离开乘客后续出行不便性，使其出行时间等于计划乘车时间乘以大于1.0 的惩罚系数ρ.每个e关联的乘客乘车时间Te,v如式（20）所示，所有出发事件对应的乘车时间合计则为总的乘客乘车时间.

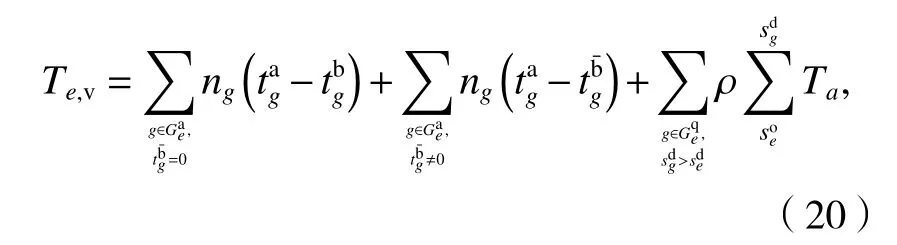
式中：Ta为从e到e′的活动a所需的时间，a=(e,e′)∈Ar∪Ad，其中Ar、Ad分别为区间运行活动集合、停站活动集合.

3 算例分析

以一条实际线路为背景，以正常运营场景为参照，分析和评估故障运营场景下的客流分布.以8∶00−11∶00 为研究时域，预先将正常运营条件下的网络OD 客流数据转化为本线OD 客流数据，形成标准客流量.如表1 所示，为了表示方便，给出了研究时域内汇总的OD 客流量.正常场景为按计划运行图、全线单一交路站站停模式运营，8∶00−9∶20 行车间隔为4.5 min，9∶20−11∶00 行车间隔为6.0 min；故障场景为假设8:00 发生故障、导致车站6、7、8 三站两区间上行（车站1 往车站11 方向）列车运行中断2 h，使用小交路折返和故障区段下行单线双向交替运行的组合调度策略，以尽量贴合计划图为目标生成的调整运行图.故障期间调整图行车间隔不再均匀，但最终恢复计划.计划图和调整图如图2 所示，其中阴影部分表示上行方向区段故障的时空范围.

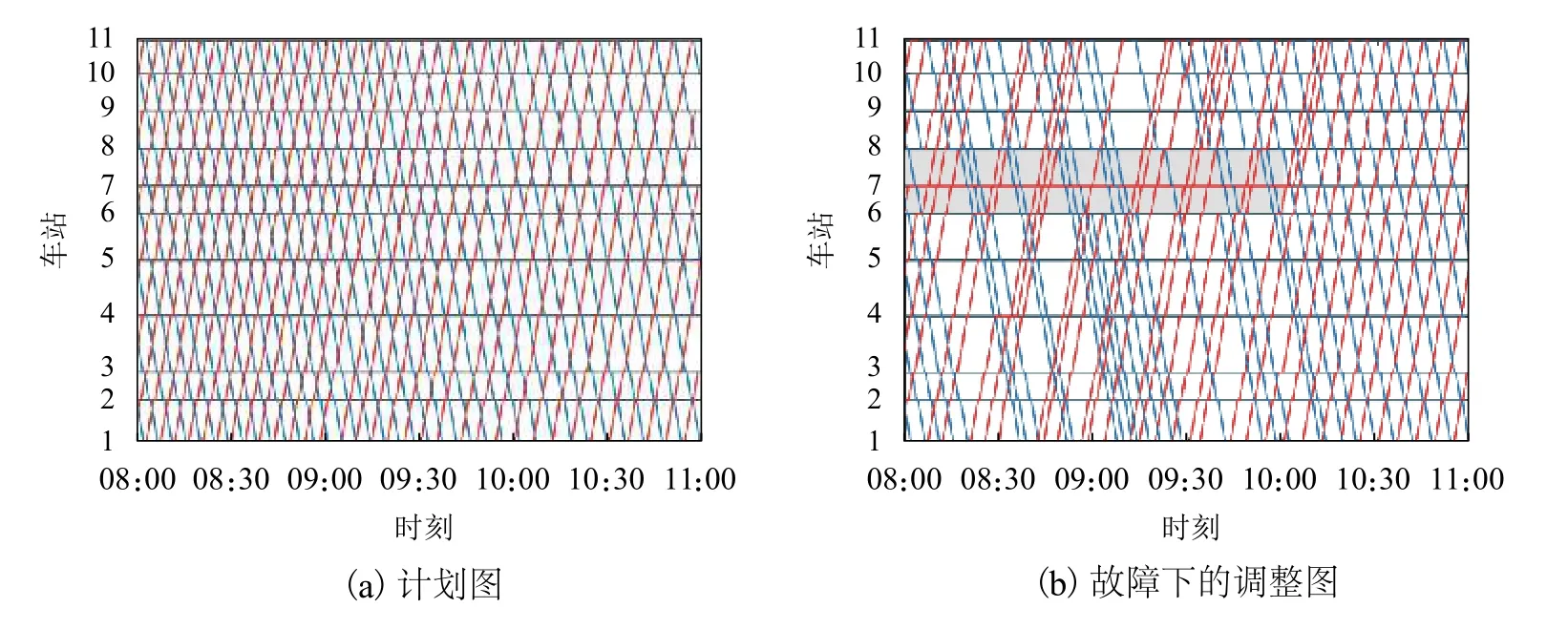
图2 运行图Fig.2 Train working diagrams

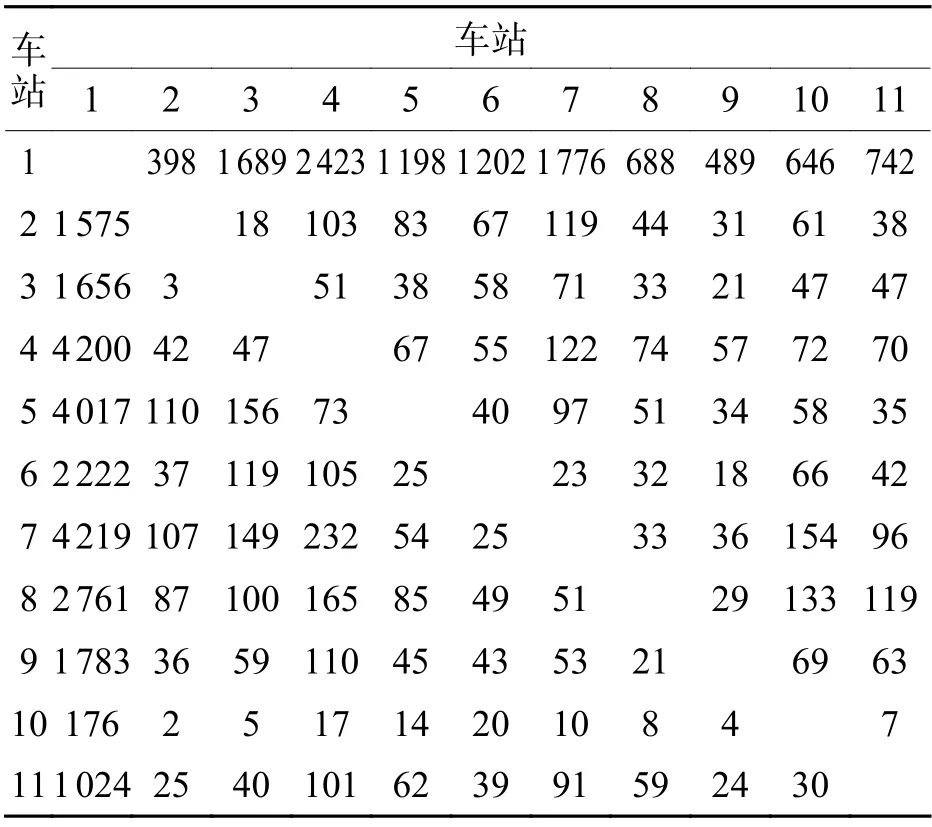
表1 汇总的OD 客流量Tab.1 Total OD volume 人

列车定员能力为840 人，列车允许最大满载率设为120%.换乘等待时间惩罚系数 δ 设为2.考虑乘客最大等待时间d和离开乘客后续出行惩罚系数ρ对客流分布的影响，分别设置不同值讨论分析：

1）d=9，10，15 min：9 min 为该线路早高峰期间行车间隔的2 倍，该取值是指无论新进站还是留乘，乘客最多等待2 个计划间隔；在此基础上，适当考虑乘客因习惯或其他方式耗时更多而愿意多等待的情况，结合等待时间对客流控制的影响研究[9]，增设10 min 和15 min 的d取值.当等待时间超过d，乘客离开，以此体现故障影响乘客行为的变化.

2）ρ=1.5，2.0：乘客当前路径被认为是最短路径，离开的乘客后续出行不便性增加，具体耗时取决于交通状况.为方便计算，这里假设离开后的出行时间为原路径的1.5 或2.0 倍.

利用本文的模型和仿真算法，分别得到上述参数条件下每个出发事件对应的客流分布结果.由于数据量大，方便起见，以下从列车满载率、站台客流分布和乘客出行时间3 个方面分析客流分布情况.

以下行（车站11 往车站1 方向）为例，列车满载率如图3、4 所示.可见部分时空范围列车满载率较高.根据计算结果，按计划图运营的正常场景下，随着d增大，唯一变化的时空满载率增加幅度未超过0.1，这说明计划图较好地满足了标准客流量，图3仅用d=9 min 条件下的结果举例.图4 给出d=9 min和d=15 min 的故障场景计算结果.对比图3 可见，故障下局部时空范围内列车满载率增大，且由于服务数减少、行车间隔增大，满载率高的时空范围有所扩大.对比图4（a）和图4（b）可见，随着d增大，高满载率的时空范围进一步扩大，因为乘客更愿意等待后续列车而非离开.

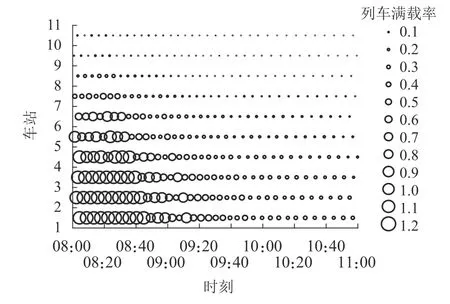
图3 正常运营场景下的列车满载率Fig.3 Train load rates under normal scenario

图4 故障运营场景下的列车满载率Fig.4 Train load rates under disruption scenario

站台客流分布结果如表2 和图5 所示.由于故障下调整图对应的列车服务数减少，站台等待、留乘、离开情况比计划增多.根据表2，在不同乘客最大等待时间下，计划图的站台人数分布指标变化不大，说明计划图与标准客流较为匹配，有留乘和离开乘客，是因为高峰期标准客流量稍大于运能.对比之下，调整图的最大站台等待人数、最大留乘人数均增加，且多等待往往意味着留乘更多，比如d=15 min与d=9 min 相比，最大留乘人数755 人，比389 人增加94.1%，相应的最大等待人数增加29.6%.但留乘乘客可乘后续列车，离开人数减少77.0%.因此d与最大留乘人数、等待人数正相关，与总离开人数反相关.站台人数的多少是客运组织较为重视的一个指标，图5 对不同场景不同d下所有服务节点对应的站台等待人数进行排序，可见故障下站台人数较多的情况更普遍，若不加管控，站台拥挤容易引起安全风险.

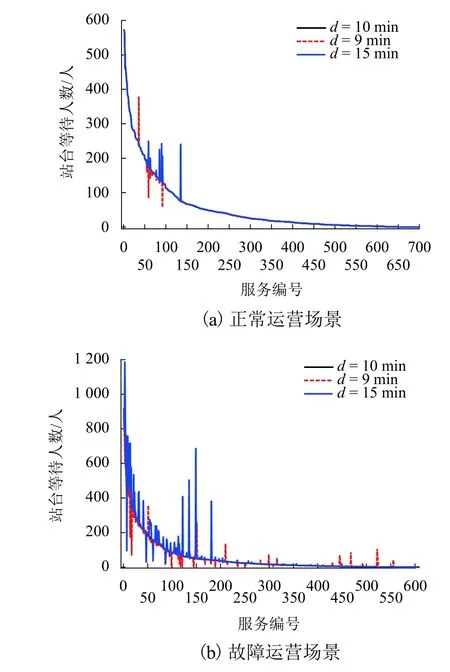
图5 所有服务的站台等待人数排序Fig.5 Sort by the number of waiting passengers for all train services

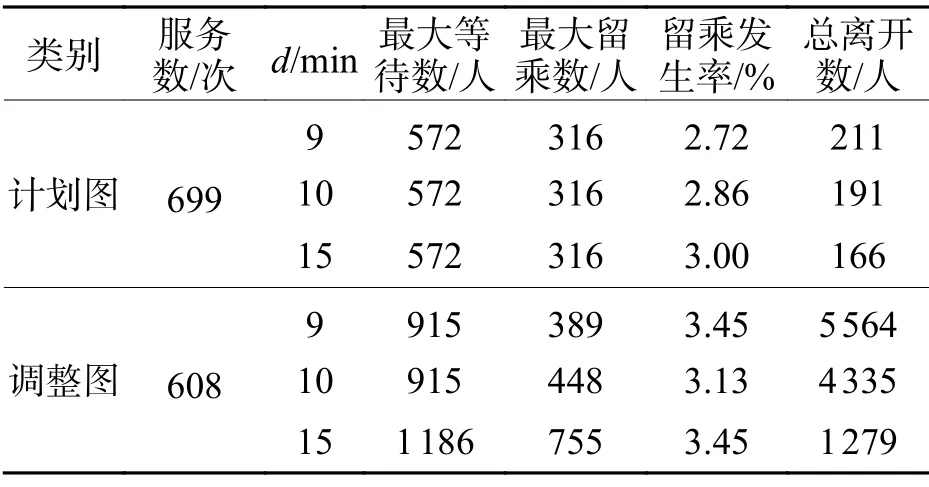
表2 站台客流分布指标Tab.2 Indexes of passenger flow distribution on platforms

乘客出行时间指标如表3 所示，总体上，故障发生时乘客总旅行时间和总等待时间都较正常情况增加不少.一般地，总的等待时间随d增加而增加，而故障下d=9 min 时，在小交路折返站换乘下一列车的情况较多，带惩罚的等待时间较大.认为乘客离开后的出行时间比在当前线路的更长，由于故障下延长等待意味着更多人不用离开，因此总的旅行时间随d增加而显著降低，15 min 与9 min 对应的乘客总旅行时间在两种 ρ 条件下分别降低10.5%、14.6%，离开惩罚系数 ρ越大，降幅越大；但正常情况下延长等待只减少很少的离开人数，而多余的等待时间反而使得乘客总旅行时间有所增加.ρ只作用于离开乘客的后续出行时间，因此其取值只与乘客总旅行时间正相关，不同 ρ值下的总旅行时间差距明显，可见乘客离开及后续选择的其他路径所需时间对出行时间影响较为显著.