一类中值定理双介值问题命题的注记
2021-10-30龚致宾楼红卫
龚致宾, 楼红卫
(复旦大学 数学科学学院,上海200433)
1 引 言
微分中值定理是微积分学中的重要内容之一,很多关于中值等式的证明往往要利用微分中值定理,但是笔者发现涉及中值定理“双介值问题”的许多例题与习题是平凡的,举例如下,其中例1,4,5,6,8可分别在文献 [1-5] 中找到.

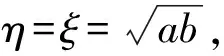
例2设函数f在闭区间 [0,1] 上连续,且在 (0,1) 内可导,证明:存在ξ,η∈(0,1)使得
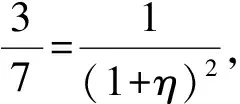
例3设0 (本题曾出现在中国科学院大学2013年研究生入学统一考试题《高等数学(甲)》中) 例4函数f在 [a,b] 上连续,在 (a,b) 内可导,证明:存在ξ,η∈(a,b), 使得 (eb-ea)f′(η)=(b-a)eηf′(ξ). 解令ξ=η,只要找是否有ξ满足 eb-ea=(b-a)eξ, 这就退化为与函数f无关的“单介值问题”,利用Lagrange中值定理易得. 例6设1 例7设 0 这些题目的共性是等式两边均含有f′,但涉及“两个中值”,题目的本意是用两次甚至多次中值定理来找到某种联结.但时常不小心因有明显满足ξ=η且与f无关的解而成为平凡的问题. 笔者发现此类命题大多数是以如下形式出现的: 设函数f在 [a,b] 上连续,在 (a,b) 内可导,则存在ξ,η∈(a,b), 满足f′(ξ)=F(a,b,ξ,η)f′(η). 而F具有形式 (1) 其中二阶连续可导函数h,g是根据F的表达式找出来的函数,必要时为了使得F(a,b,ξ,η)对任何ξ,η∈(a,b)有意义, 还会对a,b的取值作一定限制, 比如假设 0 可以猜想,出题者的本意应该是让解答者先从F(a,b,ξ,η) 的表达式找到h,g使得 (1) 成立,然后利用Cauchy中值定理(例7-8)得到存在ξ,η满足 从而得到 (2) 然而,若 (1) 成立,则利用Cauchy中值定理,有ξ=η∈(a,b) 使得F(a,b,ξ,η)=1,从而原问题有与f无关的满足ξ=η∈(a,b) 的平凡解. 那么,能否增加限制条件ξ≠η,使得问题变得不平凡且有解?对于上述提及的类型,即 (2) 式,回答是肯定的.但这时,以通常的方法直接利用中值定理来得到结论似有困难,而利用微分Darboux定理则可以比较容易地解决问题.微分Darboux定理是说区间上点点可导的实函数,其导函数具有介值性.这里,称区间I上的实函数f具有介值性是指对于I的任何子区间J,像集f(J) 也是区间.具体地, 对于双介值问题,给出如下结论: 命题设函数g,h在 [a,b] 上连续,在 (a,b) 内二阶连续可导.且∀x∈(a,b),g′(x),h′(x) 均不为零,g′ 和h′ 在(a,b) 内不恒等.若函数f在 [a,b] 上连续,在 (a,b) 内可导, 则存在不相等的ξ,η∈(a,b) 使得 (2) 式成立. 注意到 由Darboux定理,Gf′在 (a,b) 内具有介值性,同理,Hf′ 在 (a,b) 内具有介值性.要证存在不相等的ξ,η∈(a,b) 使得 G(ξ)f′(ξ)=H(η)f′(η). 由 Cauchy中值定理, 存在ξ0∈(a,b) 使得G(ξ0)=H(ξ0),从而 G(ξ0)f′(ξ0)=H(ξ0)f′(ξ0). 注意到一个实函数若在区间 (α,β) 内具有介值性且不取常数γ,则它必在该区间恒大于γ或恒小于γ.以下记γ=G(ξ0)f′(ξ0)≡H(ξ0)f′(ξ0). 证法1以下分情形讨论.除去情形 Ⅰ,Gf′和Hf′在区间 (a,ξ0) 和 (ξ0,b) 均分别恒大于γ或恒小于γ.具体情形如下表所列,其中第一列(行)每一格的正负号依次表示函数Gf′-γ(函数Hf′-γ) 在区间 (a,ξ0) 和 (ξ0,b) 内的符号. +,++,--,+-,-+,+Ⅱ.1,Ⅱ.3Ⅱ.3Ⅱ.1Ⅲ.1+,-Ⅱ.1Ⅳ.1Ⅱ.1,Ⅱ.4Ⅱ.4-,+Ⅱ3Ⅱ.2, Ⅱ.3Ⅳ.2Ⅱ.2-,-Ⅲ.2Ⅱ.2Ⅱ.4Ⅱ.2, Ⅱ.4 情形Ⅰ存在ξ1∈(a,b) 使得ξ1≠ξ0,以及下列情形之一成立: Ⅰ.1G(ξ1)f′(ξ1)=γ; Ⅰ.2H(ξ1)f′(ξ1)=γ. 对情形Ⅰ.1, 有G(ξ1)f′(ξ1)=H(ξ0)f′(ξ0).取ξ=ξ1,η=ξ0即满足命题要求. 对情形Ⅰ.2, 取ξ=ξ0,η=ξ1即满足命题要求. 情形Ⅱ下列情形之一成立: Ⅱ.1G(x)f′(x)>γ(∀x∈(a,ξ0)),H(x)f′(x)>γ(∀x∈(ξ0,b)); Ⅱ.2G(x)f′(x)<γ(∀x∈(a,ξ0)),H(x)f′(x)<γ(∀x∈(ξ0,b)); Ⅱ.3H(x)f′(x)>γ(∀x∈(a,ξ0)),G(x)f′(x)>γ(∀x∈(ξ0,b)); Ⅱ.4H(x)f′(x)<γ(∀x∈(a,ξ0)),G(x)f′(x)<γ(∀x∈(ξ0,b)). 此时,不妨设Ⅱ.1成立,由介值性,存在ξ∈(a,ξ0),η∈(ξ0,b)使得 G(ξ)f′(ξ)=H(η)f′(η). 即ξ,η满足命题要求. 情形Ⅲ下列情形之一成立 Ⅲ.1 ∀x∈(a,b),x≠ξ0有G(x)f′(x)>γ,H(x)f′(x)<γ; Ⅲ.2 ∀x∈(a,b),x≠ξ0有G(x)f′(x)<γ,H(x)f′(x)>γ. 不妨设Ⅲ.1成立,此时,∀x∈(a,b),x≠ξ0, 由上式立即有γ 情形Ⅳ下列情形之一成立 Ⅳ.1 ∀x∈(a,ξ0)有G(x)f′(x)>γ,H(x)f′(x)>γ; ∀x∈(ξ0,b)有G(x)f′(x)<γ,H(x)f′(x)<γ; Ⅳ.2 ∀x∈(a,ξ0)有G(x)f′(x)<γ,H(x)f′(x)<γ; ∀x∈(ξ0,b)有G(x)f′(x)>γ,H(x)f′(x)>γ. 不妨设Ⅳ.1成立,由于g′ 和h′ 在 (a,b) 内连续,且不恒等,因此,G和H必在 (a,b) 内无穷多个点处不相等.又由于f′至多只有一个零点,因此,必有ξ1∈(a,b),ξ1≠ξ0使得 G(ξ1)f′(ξ1)≠H(ξ1)f′(ξ1). 不妨设ξ1∈(a,ξ0),G(ξ1)f′(ξ1)>H(ξ1)f′(ξ1).则由G(ξ0)f′(ξ0)=γ 证法2反设命题结论不成立.由介值性,函数ψ≡Gf′ 和φ≡Hf′ 的像集A≡ψ(a,b),B≡φ(a,b) 均为区间或单点集.而对于任何μ∈A∩B,方程ψ(x)=μ和方程φ(x)=μ在(a,b)内的解必唯一且相等.以下分三种情形讨论. 情形aψ-1(A∩B)={ξ0}. 此时,在(a,b)内恒有ψ≤φ或恒有φ≤ψ,且等号仅在ξ0处成立.不妨设前者成立,则∀x∈(a,b),x≠ξ0,有 由上式立即有γ 情形bψ-1(A∩B)=(a,b). 此时, 在 (a,b) 内有ψ≡φ.进而G≡H,与g′ 和h′ 在(a,b) 内不恒等的假设矛盾. 情形cψ-1(A∩B)≠(a,b),{ξ0}. 此时,ψ-1(A∩B) 为区间,且其左端点α≠a或右端点β≠b.不妨设α≠a.此时作为(α,β)内满足介值性的单射,ψ和φ均是单调的.有 从而ψ(α)是A∩B的端点. 若ψ(α)是A∩B的左端点,则必有δ>0 使得 (ψ(α)-δ,ψ(α))⊂ψ(a,α).从而ψ(α) 是A的内点.同理,φ(α) 是B的内点. 这与ψ(α)=φ(α)是A∩B的端点矛盾. 若ψ(α)是A∩B的右端点,同理推出矛盾. 总之,反设不真.命题证毕. 把所列 8 个例题作一回顾,列出相应的函数g和h如下,不难见到它们是满足命题要求的. 例题g(x)h(x)区间 [a,b] 的要求区间条件可减弱为1x1/x0 本文从一类有平凡解的存在性问题出发,通过分析命题的意图,最后利用微分Darboux定理证明了非平凡解的存在性. 致谢本文受益于复旦大学数学科学学院苏步青班的无学分讨论班等.感谢相关文献对本文的启发以及审稿专家提出的宝贵意见!

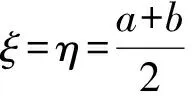
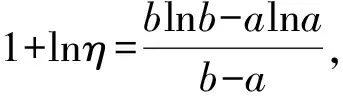
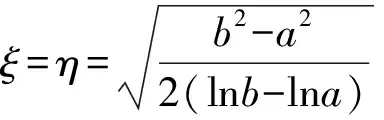
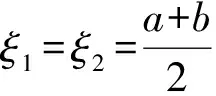
2 “双介值问题”的非平凡化
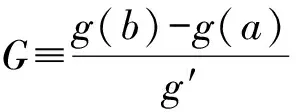
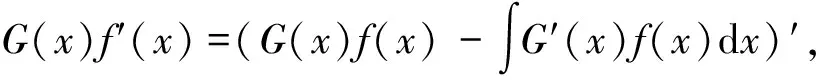

3 例题回顾
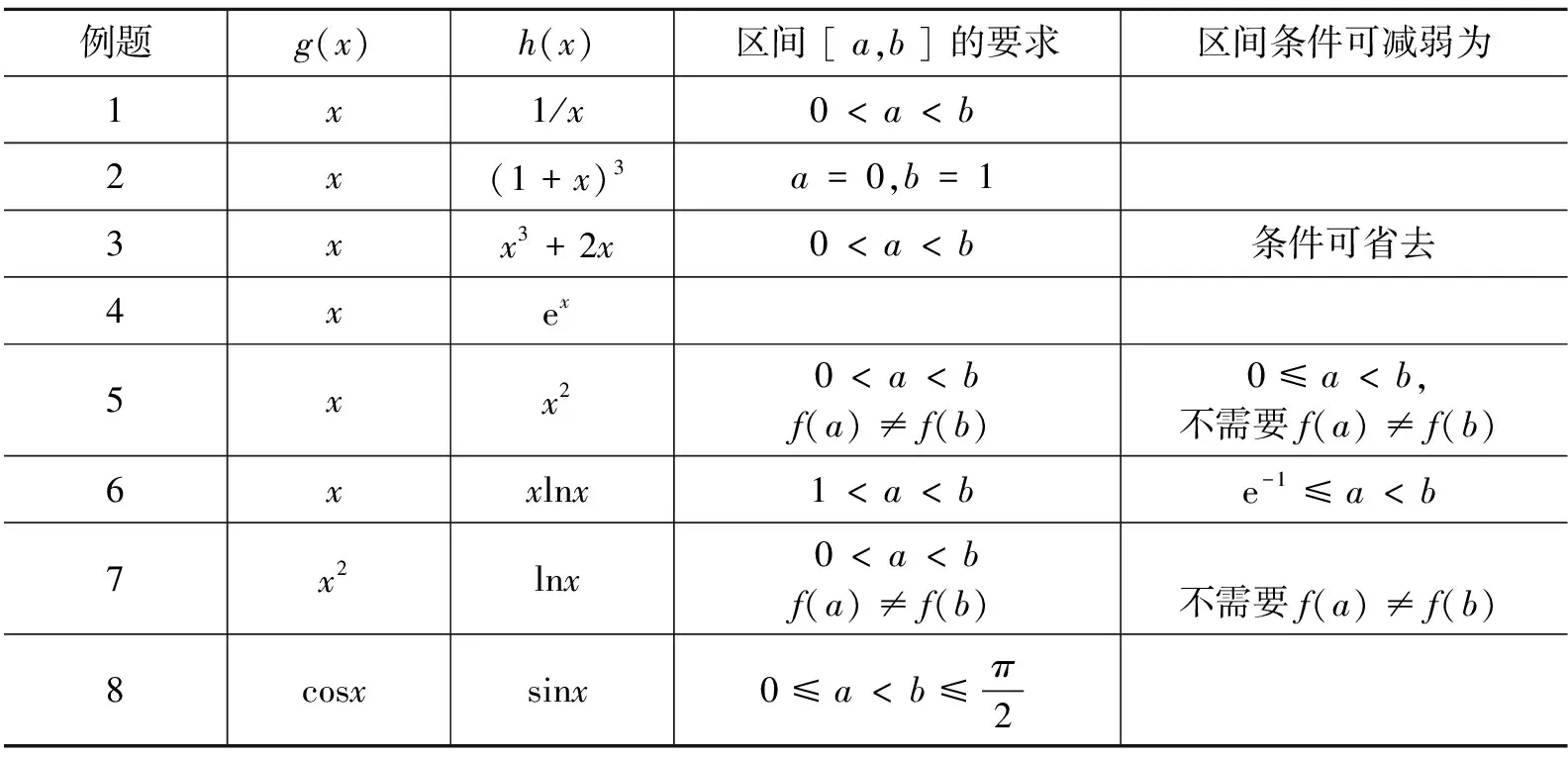
4 结 语
