基于平均数的椭圆周长近似公式
2021-10-30王青山陈晓彦
刘 植, 王青山, 陈晓彦
(合肥工业大学 数学学院,合肥230601)
1 引 言
椭圆作为圆锥曲线的一员,自古希腊阿波罗尼奥斯(Apollonios, 262-190 BC)以来就是数学的重心.这个出于人类理智思索的美丽想象,到了文艺复兴时代由于John Kepler的创见而达到高峰.随着微积分的飞速发展,得到了精确计算椭圆面积的初等公式,却没有找到精确计算椭圆周长的初等公式.事实上,椭圆的周长是一个积分(事实上因为椭圆的缘故我们称之为椭圆积分),这是一个超越函数,所以在实际应用中必须诉诸于近似公式.
为叙述方便,这里设a,b为一椭圆的半长轴和半短轴的长,L(a,b)表示该椭圆的周长.利用积分方法计算椭圆周长时,结论表示为第二类椭圆积分,其原函数无法用初等函数表示,因此椭圆没有精确计算周长的初等公式,只能展开为无穷级数的形式[1].1742年,苏格兰数学家Colin Maclaurin(1698-1746)首先给出按离心率展开的椭圆周长级数表达式
也即
(1)
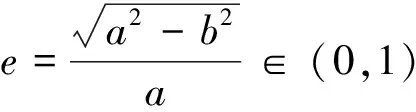
在机械制图中常用“四圆心法”作椭圆的近似图形,这种方法是用四段圆弧来代替完整的椭圆周,用圆弧的长代替椭圆弧的长,从而求出椭圆周长的近似值.黄[2]和李[3]分别研究“四圆心法”并得到了椭圆周长的近似计算公式
何[4]通过改进上述公式,使其相对误差降低了10%.周[5]给出计算椭圆周长近似值的另一种作图解法,将椭圆弧近似为一直线段,并导出了相应的近似计算公式.此外,张[6]研究了另一种直角三角形几何作图法求解椭圆周长,也给出了相应近似计算的公式.然而,上述基于几何作图方法得到的若干近似公式误差较大,只适用于精度要求不高的场合.
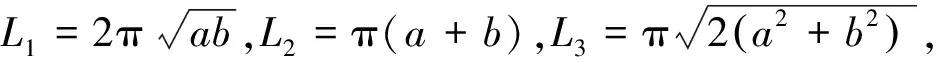
为了构造具有更高精度且形式简单的近似公式,本文构造了基于调和平均数的椭圆周长近似公式,结合现有其他基于平均数的近似公式,利用加权平均的方法得到椭圆周长的一个新的高精度近似公式,与现有其他基于平均数方法的近似公式相比,计算精度得到很大提升.
2 基于调和平均数的椭圆周长近似公式
调和平均数是一类重要的平均数,常用在相同距离但速度不同时平均速度的计算问题中.可以利用调和平均数方法构造椭圆周长的近似公式如下:以椭圆两个半轴a和b的调和平均数
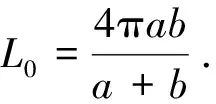
展开即得
类似的,文献[7]与文献[11]中基于平均数的近似公式也可展开为级数形式
3 基于平均数的椭圆周长高精度近似公式
注意到L0,L1,L2以及L3展开式中的前两项均与精确公式(1)是一致的,若将他们重新优化组合,可以得到精度更高的近似计算公式.为此,可设
Lij=αLi+(1-α)Lj(i,j=0,1,2,3).
确定参数α的值使得新近似公式Lij的精度尽可能高.由此可得
事实上,L12即为Peano在1889年给出的近似公式[12],也是目前普遍采用的近似公式之一.用类似方法,可得到具有更高精度的近似公式
通过比较容易看出,L01,L12,L23均与精确公式(1)的前四项一致;L012和L123均与精确公式(1)的前六项一致;而L0123与精确公式(1)的前八项是完全一致的,也是本文得到精度最高的近似公式.
各近似公式间的关系如下图,在实际应用中可以根据误差要求选择适当的公式近似计算椭圆的周长.
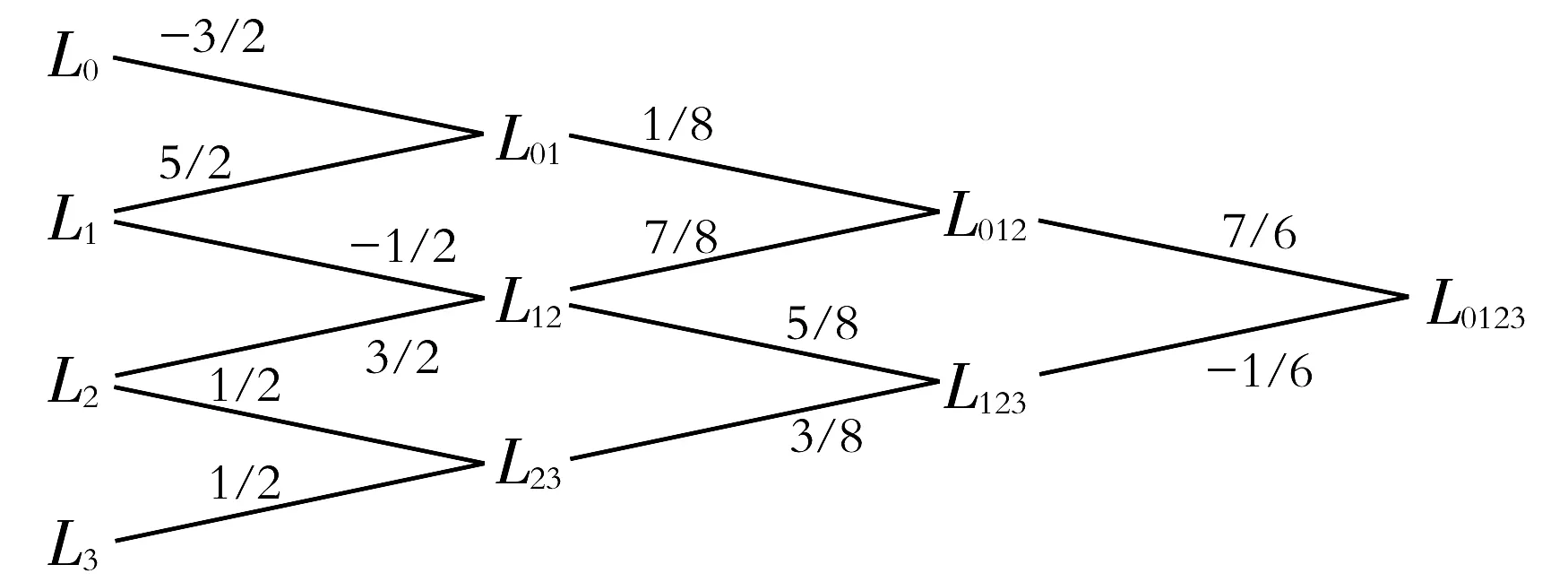
图1 基于平均数的椭圆周长近似公式关系图
由于上述级数都是按离心率展开的,故近似计算公式对离心率小的椭圆(通常称为圆椭圆)效果更好,对离心率大的椭圆(通常称为扁椭圆)来说收敛较慢,逼近效果较差.
4 数值实例
为检验本文方法的有效性,比较各公式间的差异,针对不同数据的椭圆利用近似公式分别计算周长,具体数值如下表:
根据表1,a=b时,各种方法都能得到精确的周长;横向从左往右随着a与b之间差距的扩大,各公式的精度越来越差;纵向从上往下随着近似公式的重新组合,各公式的精度越来越好;L0123已经具有相当高的精度.
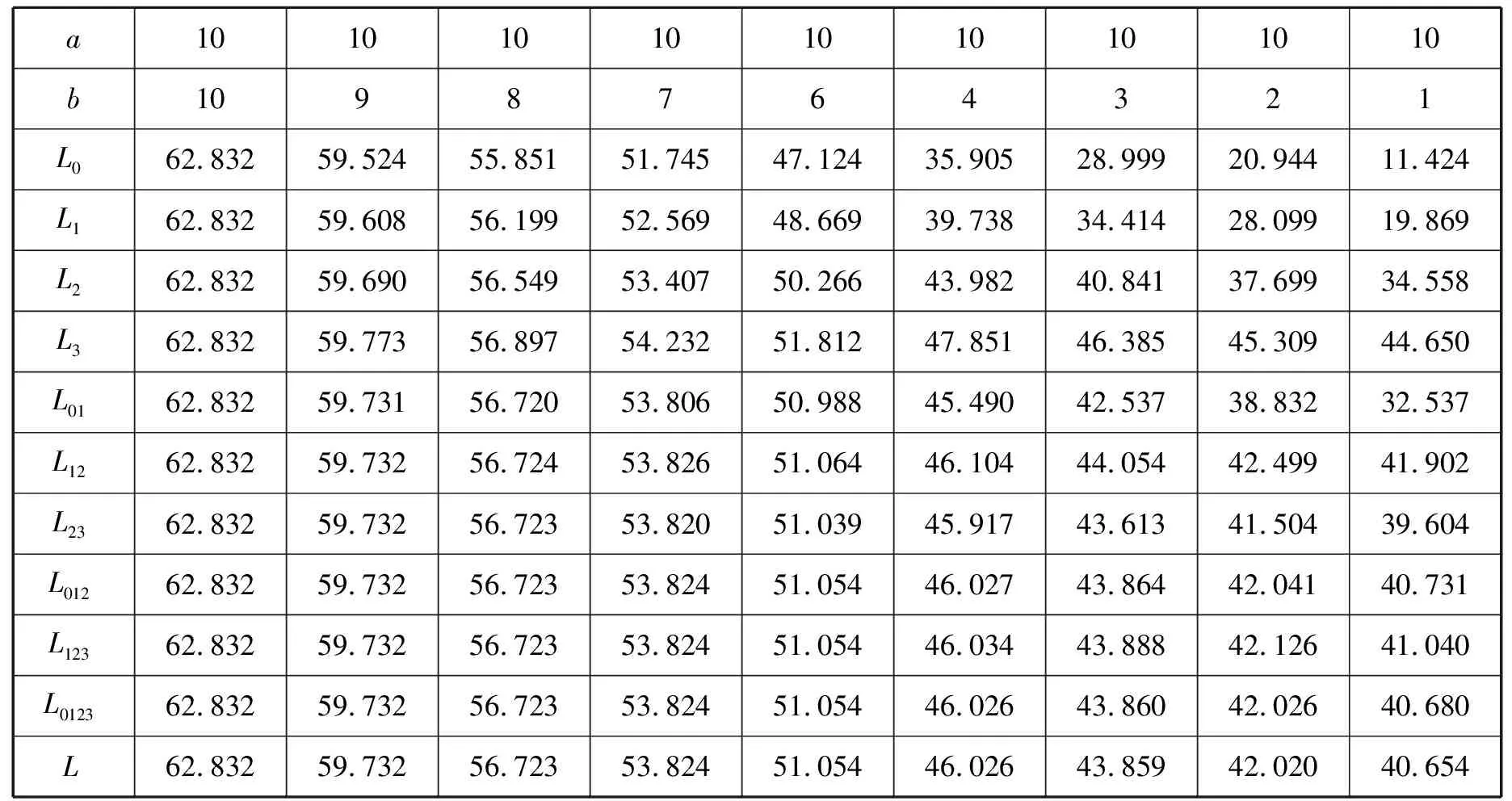
表1 椭圆周长表
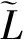
表中数值是应用MATLAB取15位有效数字计算的,因此,精度超过15位的误差数值表示为0.由表2可以看出,用本文方法得到的近似公式L012、L123和L0123计算地球子午线长度时,已经达到相当高的精度,这说明本文得到的高精度近似公式是简单、有效的.
表2 子午线长度近似计算误差对比
5 结 论
本文利用调和平均数方法构造了一个椭圆周长的近似计算公式,虽然直接以上述公式计算误差较大,但通过加权优化组合以后得到的新公式的误差大幅减少,其中L0123是基于平均数方法中具有最高精度的近似公式.数值实例表明,该公式是有效的.
致谢作者对贵刊审稿人提出的宝贵意见表示衷心感谢,文[7]和[11]对作者的写作有了很大的启发,对此表示感谢.
