一类级数求和问题推广的再讨论
2021-10-30苏灿荣
苏灿荣, 周 玲
(合肥工业大学 数学学院,合肥230601)
1 引 言
课堂教学是培养高质量人才的主战场,教师如何在课堂培养学生学习高等数学的兴趣,是一线数学教师共同面临的课题.笔者认为鼓励学生利用已有的知识不断探索一些习题是提高学习积极性的途径之一.
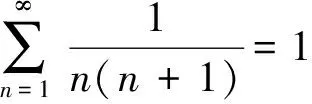
结论1设m为非负整数,则
(1)
结论2设m为正整数,则
(2)
结论3设l,m为正整数,且l (3) 结论4设m为非负数,l为正整数,则 (4) 文[1]所得的四个结论最重要的是结论一,这是因为对结论一级数通项分母中的字母或乘积项数的变更或扩充,再通过一些运算技巧便可得到结论二、三、四.如果将结论一中级数通项在更广的范围考虑,我们将会得到比结论一更一般的结果,由此便可进一步对结论二、三、四作出推广.推广后的结论如下. 推广1设a≥0,d>0,l≥0,则 (5) 推广2设m为正整数,a≥0,d>0,则 (6) 推广3设l,m为正整数,且l (7) 推广4设m为非负数,l为正整数,又a≥0,d>0,则 (8) 推广1的证明所给级数的部分和 故级数的和 即(5)式成立. 特别在(5)式中取a=m,d=1,l=0,即得(1),因此(5)为(1)之推广. 推广2的证明 利用推广1的结果,则有 即(6)式成立. 特别在(6)式中取a=0,d=1,即得(2),因此(6)为(2)之推广. 推广3的证明 利用推论2的结果,则有 即(7)式成立. 特别在(7)式中取a=0,d=1,即得(3),因此(7)为(3)之推广. 推广4的证明对l运用数学归纳法. 由(5)知 故当l=1时(8)式成立. 设l时(8)式成立,则当l+1时, 由归纳法假设, 故l+1时(8)式成立,因此对任何正整数l,(8)式成立. 特别在(8)中取a=0,d=1即得(4),因此(8)为(4)之推广. 最后要说明的是,在本文所得的四个推广中对其中的参数赋予不同的值,可求得很多级数的和,这里不再举例说明. 数项级数的求和是一个较难的问题,高等数学中通常有裂项相消求和;利用已知级数求和;通过解方程求和;利用幂级数求和等方法.而本文主要是基于裂项相消及恒等变形思想,对一类级数求和推广的再推广,一方面为教学提供有益的素材,另一方面通过推广形式,培养学生的创新意识和能力. 致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.2 主要结果
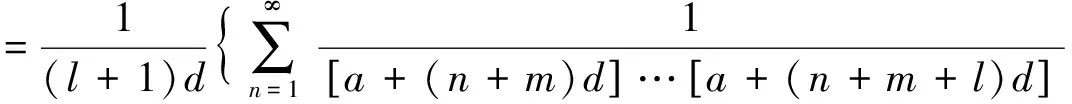
3 结 论
