基于LES模拟的微沟槽湍流减阻特性数值研究

朱 涵，黎义斌，李小斌，郭东升，张红娜，李凤臣

(1.兰州理工大学能源与动力工程学院，甘肃 兰州 730050；2.天津大学机械工程学院，中低温热能高效利用教育部重点实验室，天津 300350；3.中山大学中法核工程与技术学院，广东 珠海 519082)

湍流减阻对水上船舶、潜艇、飞机以及长输油管道等运输工具的节能减排具有重要意义.在流体中运动的物体会受到摩擦阻力和压差阻力，消耗了绝大部分能量，并且在超音速的飞行器还会受到激波阻力，这三种阻力占比中，其中摩擦阻力约占总阻力的40%～50%[1].由于阻力与航速呈平方关系，与推进功率呈三次方关系[2]，减小摩擦阻力对提高航速、航程和节约能源具有重要的意义.

沟槽减阻技术，即在物体和流体接触的表面上布置微小的纵向沟槽，以达到湍流减阻的目的.该技术实际也是效仿鱼类的仿生减阻技术之一，纵向沟槽在物体表面的布置，将一定程度上改变与粘性阻力紧密相关的湍流拟序结构，抑制了涡结构的发展，在适当条件(如一定的雷诺数Re范围、沟槽尺度)下具有明显的减阻效果，该技术在管道输送、航天、机械设备及体育运动中已有运用的实例.李育斌等[3]在1∶12的机翼模型表面具有湍流流动的区域顺流向粘贴肋条薄膜后，进行试验后发现可减小阻力5%～8%；南京航空航天大学的潘家正[4]提出了“微型滚动轴承”理论，在湍流边界层底部按照一定间距横向分布的沟槽能锁住流动的小涡，并获得了约10.2%的减阻效果；KSB公司[5]也在多级泵的叶片表面加工了一定形状的沟槽后，发现综合效率提高了1.5%.另外，在管道流动中，内壁面带微肋条/沟槽结构的计算中，也获得了流动阻力减小[6-7]及传热效果改善的结论[8-9].可见，在相应平面上布置沟槽形状，可以起到减阻增输的效果.

在沟槽减阻的机理研究方面，大部分理论认为沟槽面上湍流边界层的粘性底层增厚，近壁区的湍流强度、雷诺切应力降低.粘性底层增厚，使得局部表面摩擦阻力(粘性切应力)降低，实现减阻.另外，从湍流结构上来讲，部分理论认为湍流拟序结构在沟槽面上发生了变化，大尺度涡结构减弱，从而降低了阻力.沟槽结构减阻的研究尽管有了较大发展，但仍有许多问题需要解决，如大Re数条件下的流动减阻机理、沟槽适用性等内容需要深入研究.

早期已有许多学者对纵向微沟槽在牛顿流体中的性能进行了数值模拟研究，但对纵向微沟槽在牛顿流体中的减阻机理依然不完善，且绝大多数研究针对于较大尺度的沟槽宽度及很小的尖峰宽度，如V型、薄肋片式矩形等纵向微沟槽[10].但上述沟槽结构易受到流体动力学破坏且减阻范围限制较大，大尺度的沟槽不能适应高速流动的减阻需求.本文通过参考鱼类等仿生结构，建立了微米尺度的纵向沟槽微结构，沟槽构型为半圆形.分别对光滑平板和微沟槽面的湍流流场进行了大涡模拟，观测了沟槽壁面湍流边界层的拟序结构和流动特征，并定量分析了沟槽的减阻效果及其减阻机理.

1 数值计算方法及结果验证

为了分析沟槽表面的减阻效果，对光滑表面和沟槽表面分别进行数值模拟，对比两者的流动特性.

1.1 模型建模及边界条件

光滑平板几何结构如图1(a)所示，其流向长度为0.1 m，法向高度为0.04 m，展向宽度为0.04 m.对于带沟槽表面，参考仿生结构，设计了沟槽为半圆形构型，其沟槽宽度s为60 μm，深度h为30 μm，间隔t为20 μm，单个沟槽形状见图1(b).考虑到沟槽宽度很小，且欲构建的沟槽数量较多，整体建模困难，故其整体结构通过单沟槽阵列获得.此沟槽流向长度和法向高度均与光滑平板结构相同.

图1 流体域几何模型示意图

在边界条件设置上，主要流动能量消耗在固体壁面上，将下壁面设定为无滑移壁面.因研究目标为充分发展状态下的湍流流动结构，而湍流需要经过层流区、过渡区才可发展成湍流，为节能计算资源，将流向方向(+z)上的前后面设置为周期性边界，流体在流向上的运动通过设置流向上的质量流量来驱动.在展向方向(x)上，沟槽模型的网格数较多，亦将展向两侧面设置为周期性边界.

1.2 计算域网格划分及网格无关性验证

光滑平板的网格划分如图2(a)所示，采用结构化网格划分，流向均匀分布200个网格，展向上均匀分布100个网格，为了捕捉到近壁区的拟序条带结构(如“上扫”与“下掠”)，在法向(+y)上采用边界层加密，法向上对数分布100个网格，第一层网格为10 μm，增长比例为1.005，整体网格数为210万.对于沟槽结构，如图2(b)所示，也采用结构化网格，微沟槽模型流向均匀分布200个网格，法向上对数分布50个网格，在一个单元体结构内，展向分布8个网格.整个沟槽面阵列个数为50，总体网格数为410万.

网格无关性验证结果如图3所示，以光滑平板为例，改变模型的网格划分尺寸，分别生成170万、190万、200万、210万、220万、230万六种网格数量.通过监测下壁面上的剪切应力，发现在网格数量210万之后，剪切应力结果几乎不再改变.210万网格数与220万、230万数计算误差分别等于0.094%、0.157%，同时210万网格数与200万、190万、170万网格计算计算误差分别等于0.535%、1.794%、4.942%.可见当光滑平板网格数在210万左右时，计算结果趋于稳定，故以此作为计算标准；按照相同的分析方法对微沟槽结构模型网格进行无关性验证，得到微沟槽网格数量为410万.

图3 光滑平板网格无关性验证

1.3 湍流模型及数值计算方法

为了尽可能捕捉到流动中的细节结构并节能计算量，本文数值计算选取大涡模拟方法.大涡模拟理论有两个基本假设，即(1)湍流的平均特性，由大尺度流动相干结构控制，而小尺度湍流结构的影响基本可以忽略；(2)高雷诺数下的小尺度湍流体现出各向同性的特点[11-13].故数值模拟重点放在比网格尺度大的大涡运动上，并通过引入模型来模拟小尺度的小涡运动，该模型称为亚格子应力模型.这里选用WMLES(Algebraic Wall-Modeled LES Model)亚格子模型，在WMLES中，仅在对数层的内部激活模型的RANS部分，而边界层的外部则被修改的LES公式覆盖.由于边界层的内部流动决定于LES模型的雷诺数，因此WMLES方法可以相同的网格分辨率应用于不断增加的雷诺数，以进行流动模拟.WMLES模型是一种利用空间尺度过滤的结构函数模型.其代数表达式结合了混合长度模型、修正的Smagorinsky模型以及Piomelli的壁阻尼功能，其中涡黏度定义为

μt=min[(κdw)2，(CSmagΔ)2]·S·{1-exp[-(y+/25)3]}，

(1)

公式中：dw为计算点与壁面间距；S为应变率张量；参数κ=0.41、CSmag=0.2；滤波尺寸Δ根据特定的流场条件进行选取，有

Δ=min(max(Cw·dw；Cw·hmax；hwn)；hmax)，

(2)

公式中：hwn为沿壁面法向的网格步长；hmax为壁面网格的最大步长；Cw为通过实验确定的常数，取值0.15.

在离散方法的选取上，梯度项采用Least Squares Cell Based进行离散，压力项采用Body Force Weighted进行离散，动量项采用Bounded Second Order Differencing格式，瞬态项采用Bounded Second Order Implicit.速度和压强之间的迭代关系，采用PISO相邻校正算法进行求解.时间步长的选取对 PISO算法的精度非常重要，当在预测修正过程中，使用越小的时间步长，可取得越高的时间精度.在计算完成后，通过湍涡周转时间τ=(ν/ε)1/2对时间步长进行后验，其中，ν为运动粘度，ε为湍动能耗散率.步长选取为1×10-4s，小于一个湍涡周期，符合精度要求.

1.4 模拟方法的可靠性验证

为了验证数值模拟方法的准确性，以光滑平板为模拟对象，计算3个不同来流速度(即不同Re数)下的摩擦系数cf.

分别以流场法向高度H及边界层厚度δ99为特征尺度定义的Re数为

(3)

公式中：ρ为水的密度；U为来流速度；μ为流体的动力粘度，这里流体的水介质.

壁面摩擦阻力为

F=τwΑ，

(4)

公式中：τw为壁面剪切力；A为壁面表面积.

摩擦系数cf定义为

(5)

根据边界层理论，在光滑平板上，cf与Reδ99的理论关系式为一隐式关联式：

(6)

在边界层流动中，流向速度沿法向高度增加而增加，当速度达到平均来流的99%时，此时高度可认为是边界层厚度δ99.以此计算出Reδ99，并反推出cf，获得cf计算值与理论值的对比如图4所示.可见计算值与理论值十分接近，说明LES的计算结果是准确的.在湍流流动结构方面，进一步给出来流速度7 m/s时的速度分布与速度脉动统计规律.该工况下，对应ReH=2.8×105，Reδ99=1.2×105，流向平均速度分布和速度脉动均方根分布，如图5所示.从图5可以看出，计算结果和壁湍流理论规律吻合很好，同时从湍流脉动强度随法向高度的变化分布来看，分布合理.说明LES方法能获得理想的计算结果，及本文方法适用于牛顿流体的壁湍流流动问题.

图4 cf计算值与理论值对比

图5 来流7 m/s时的速度分布与速度脉动统计规律

2 结果及分析

在验证了计算结果的可靠性之后，下面给出沟槽减阻流动的特性及流场结构分析.

2.1 微沟槽减阻效果分析

本研究中，针对具有较宽尖峰宽度的半圆形纵向微沟槽进行分析，沟槽宽s=60 μm，深h=30 μm，间隔t=20 μm，t/s=0.33.定义无量纲沟槽宽度s+为

(7)

公式中：ν为运动粘度；cf为光滑平板的摩擦系数.

通过对比沟槽结构与光滑平板所受到的摩擦阻力，减阻率η的计算如式(8)所示，若η>0，表示微沟槽表面实现了湍流减阻，反之则为增阻.

(8)

计算不同来流速度下的减阻效果η，结果如表1所示.可以看出，沟槽结构表面在来流10 m/s以下均出现了明显的减阻效果，但随着雷诺数的增大，减阻效果先增大后减小，并在ReH=2.8×105时，减阻效果达到最大，此时减阻效果为19.11%.来流20 m/s的工况，沟槽表面的阻力相比光滑表面增加，即此时沟槽出现了增阻效应.

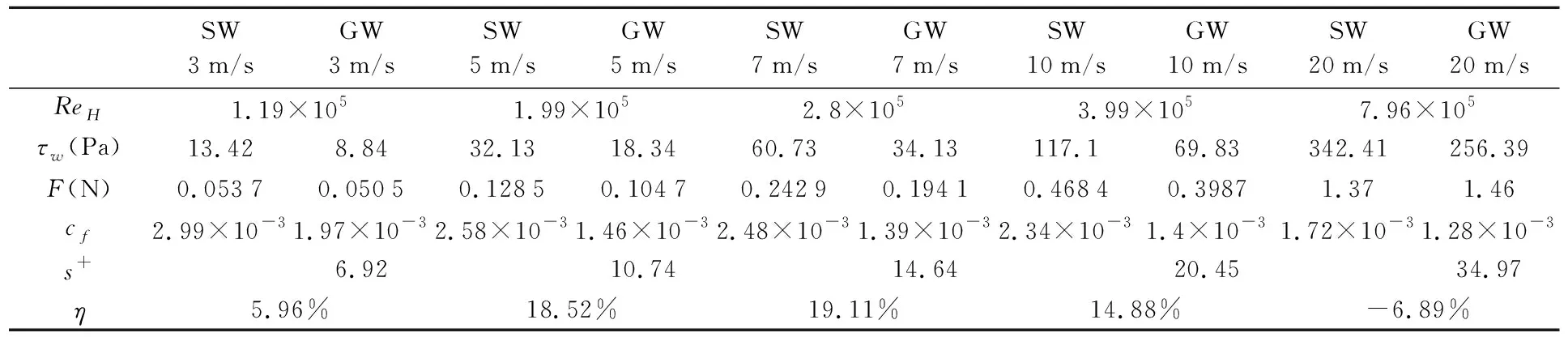
表1 沟槽表面减阻效果

沟槽表面减阻率η随s+变化的趋势，如图6所示.可以看出，减阻率先随着s+的增大而增大，而在s+=14.64时达到最大值.在工况s+=34.97时出现负值，出现了增阻效果.从无量纲沟槽宽度s+定义出发，该参数实际和以s为特征尺度的Re具有同等的意义，说明在相同的沟槽尺寸下，减阻效果跟湍流流动状态有着密切的联系，这将在下面进行深入讨论.

图6 减阻率随无量纲沟槽宽度变化趋势

2.2 涡结构数值分析

首先从沟槽表面的速度统计进行分析，然后再进行涡结构分析.沿法向设置用于速度统计的监测线，如图7所示.该监测线具体位于光滑平板壁面上方以及沟槽谷内外上方.通过上述监测线，提取近壁面位置处的瞬时流向速度以及经过时间统计后的平均速度分布.

图7 法向监测线布置示意图

平均来流速度7 m/s时流向速度沿法向的分布，如图8所示.此时沟槽表面s+=14.64.对沟槽工况来说，y+<0表示所在法向位置位于沟槽谷内，y+>0在沟槽之外，对于光滑平面来说，法向y+均大于0.

图8 不同y+值的流向速度分布(来流速度7 m/s)

红色实线为层流情况时抛物线速度分布曲线，如图8所示.该抛物线与沟槽谷内的瞬时速度分布(黑色实线)及时间平均速度分布(黑色虚线)均比较吻合，说明此时沟槽谷内大部分为层流流动，涡的侵入现象很少.在该工况下，微沟槽通过其纵向结构，使得在沟槽上方出现了“微型滚动轴承现象”，将流体与壁面的高速流动转化为流体与流体间的高速流动，亦即造成了表面的部分滑移，从而减小了流动阻力.

来流速度7 m/s时，涡结构及其壁面其应力分布规律，如图9所示.图9中给出了光滑表面与沟槽表面流场涡结构特征.其中，使用Q准则作为涡结构识别的判据，两者阈值相同.整体涡结构可见，沟槽结构出现的涡大多为升起的法向涡，而在光滑平板中有较多流向涡与壁面频繁的冲刷，以致光滑平板产生了较高的剪切应力.

图9 光滑壁面与沟槽结构表面流场涡结构(Q准则，Q=6×104)

针对不同来流速度的工况，涡结构的对比分析.同样使用Q准则作为涡结构判据，如图10所示.Q的阈值为Q/Qmax=0.007.可以看出，对应来流5 m/s和7 m/s，s+等于10.74和14.64，同样涡结构大部分为升起的法向涡，且与沟槽壁面直接接触的涡结构数量较少.相对比来流20 m/s的工况，s+=34.97，沟槽谷内有较多涡侵入，破坏了沟槽内固有的粘性底层，速度梯度增加明显，故反而将出现增阻效果.上述结果也印证了s+<30，一般为减阻区间，而s+>30时，流动阻力相比光滑表面增加.

图10 沟槽结构涡结构分布对比(阈值Q/Qmax=0.007)

2.3 低速条纹结构特性

在壁湍流中由于近壁面区不断升起和下沉的涡结构，如图11所示.会在不同法向高度的平面内呈现不同量级的低速区和高速区相间的速度分布，称为低速条纹分布.图中也给出了来流速度5 m/s时，截取y+=5光滑平板与沟槽结构的流向速度分布图，可见其分布着低速条纹.低速条纹的出现，伴随着涡结构的生长和消散，其密集程度也代表了漩涡产生的概率.下面进一步阐述在光滑表面及沟槽表面上的低速条纹结构分布.

针对两种壁面，如图12所示.在法向高度40 μm处建立了一条沿展向的监测线，在光滑平板中，该线位于y+=10处，而在沟槽结构中，该线则位于y+=6.7处.

以来流速度7 m/s为例，在光滑平板与沟槽结构里，如图13所示.不同流向位置处的流向速度w对展向距离的自相关分析结果Corr(w，w).通常可认定自相关函数Corr(w，w)中原点和第一个正峰值之间的距离可作为近壁低速条纹展向空间尺度的量度.显然，该距离越小，说明低速条纹越密集，涡结构的演化越频繁.

图13 流向速度对展向距离的自相关函数

由图13可以看出，光滑平板不同流向位置处的条纹间距在Δx+=98～176之间，而沟槽结构的条纹间距在Δx+=527～555之间，即光滑平板的条纹间距要远小于沟槽结构中的条纹间距，说明在光滑平板的壁湍流结构中有着较多的湍流流向条带分布，壁面和涡结构的相互作用十分频繁，故易产生较大的摩擦阻力.

3 结 论

本文针对高雷诺数条件下微米级半圆形微沟槽结构的湍流减阻特性进行了数值模拟和结果分析，结果发现，在雷诺数ReH=1.99×105～7.96×105范围内，半圆形沟槽结构有较高的减阻率，但在来流20 m/s条件下，相比光滑结构出现了增阻现象.在合适的雷诺数下，微沟槽结构在纵向上会形成“微型滚动轴承现象”，降低了壁面与流体之间的摩擦阻力，而在高雷诺数下，形成更细小的涡旋结构时，涡旋会侵入到沟槽谷内，故会出现增阻效果.沟槽结构的减阻效果还与沟槽尖端结构有关，尖端结构会阻碍展向涡的运动，使得沟槽结构在展向上分布较少的湍流条带，提高了减阻效果.因此，微沟槽结构减阻效果是由其结构的横纵向减阻效果共同作用的.