基于空间自回归模型的电力系统中长期负荷特性分析与预测

王秋惠

(上海和运工程咨询有限公司，上海 200000)

中长期负荷的变化与特性，是电力规划及运行部门研究的重要内容.负荷的大小与特性，对于电力系统的设计和运行来说极为重要[1].在商业化运行体制下，做好负荷预测特别是中长期负荷预测与分析工作直接关系到电网运行的成本和供电公司的切身利益.

现有的负荷特性分析方法主要有两类[2].一类是按影响因素分析，即逐个分析影响电力负荷特性的因素；另一类是分行业分析，即先对各行业的负荷特性进行分析，再叠加得到研究区域的负荷特性.

现有负荷特性分析及预测方法从时间角度对负荷与各影响因素做了相关性分析，结果表明电力需求与社会经济发展之间的相关性较强.随着社会经济和理论研究的发展，越来越多的文献和研究注意到变量的空间相依性.研究表明，地理位置的邻近性与经济、文化发展有密切的关系[3-4].全国经济增长的空间统计分析显示，全国各省份经济发展(以GDP为标准)之间的空间相关性非常明显.

空间自回归模型[5]的研究兴趣就在于发掘相关变量之间是否存在空间的相依性并探索这种相依性大小，同时由于空间自回归模型能够给出合理而有意义的数值，从而引起了广泛的关注.

本文依据统计年鉴数据，利用空间自回归模型对全国各省电力需求与GDP增长率之间的空间相依性进行了分析.空间相关指数(Moran I)计算结果表明，用电量与GDP之间在空间上具有较大的正相关性.最后，建立了基于空间自回归模型、灰色GM(1，1)和BP神经网络的组合预测模型，预测结果显示，计及了电力需求与GDP空间相关性的组合预测模型具有较高的预测精度.

1 空间自回归模型及其相关指数

1.1 空间自回归模型

空间位置特性使得地区数据也会存在相关性，这种相关性与时间序列相关性类似，称为空间自相关.空间自回归模型作为描述数据空间关系的基本模型已经有了较多的研究.空间自回归模型[6]的一般形式为

y=ρW1y+Xβ+μ，
μ=λW2μ+ε，
ε-N(0，σ2，In)，

(1)

公式中：β为解释变量X的参数向量；ρ为空间滞后相关变量的参数；λ为残差空间自回归(空间AR)结构中的参数.W1和W2为空间加权矩阵，分别对应于因变量以及扰动项中的空间自回归过程.

当ρ=λ=0时 ，为传统的回归模型 ，它意味着模型中没有空间特性的影响；

当ρ≠0，β=λ=0时，为一阶空间自回归模型.这个模型类似时间序列分析中的一阶自回归模型，反映了变量在空间上的相关特征，即所研究区域的被解释变量如何受到相邻区域被解释变量的影响；

当ρ≠0，β≠0，λ=0时，为混合回归与空间自回归模型.在这个模型中，所研究区域的被解释变量不仅与本区域的解释变量有关，还与相邻区域的被解释变量有关；

当ρ=0，β≠0，λ≠0，为残差空间自回归模型.注意到这个模型可以改写为

(In-λW)y=(In-λW)Xβ+ε，

(2)

说明所研究区域的被解释变量(Y)不仅与本区域解释变量(X)有关，还与相邻区域的被解释变量以及解释变量有关.

1.2 模型参数估计

令：A=I-ρW1，B=I-λW2，则模型(1)可以等价表示为

(3)

再根据ε服从正态分布的假设，可以得到如下对数似然函数：

(4)

通过直接最大化对数似然函数(4)即可实现对模型参数的估计.

1.3 空间相关性检验

Moran最早提出了检验回归模型空间自相关的MoranI检验[7]，该检验到目前为止依然是使用最广泛的检验，它的最大优点是计算简单.检验区域变量的空间相关性存在与否，空间统计学一般使用空间统计量——空间自相关指数MoranI.MoranI定义为

(5)

当残差服从正态分布，I统计量服从正态分布，则I统计量的期望和方差：

E(I)=tr(PW)/(n-k)，
V(I)=[tr(PWPW′)+tr(MW)2+(tr(PW))2]/d-E(I)2，
P=I-X(X′X)-1X′，
d=(n-k)(n-k-2)，

(6)

公式中：k为回归模型参数的个数；n为所分析的区域数.

2 组合预测模型的建立

2.1 组合预测模型[2]

假设某一预测问题应用了m种可行预测方法，其中第i种预测值为fi，则组合模型预测可以描述为

(8)

(9)

公式(7)、公式(8)是公式(6)的约束条件.

设y为实际值，则组合预测模型的绝对误差可以表示为

(10)

组合预测的关键在于怎样确定组合权系数ωi.在进行组合预测时，总希望权向量应使误差e越小越好，则组合预测问题可以转化成以下条件极值问题：

(11)

这样就可以将组合预测模型变换为以权系数为变量的优化问题进行求解.

2.2 计及电力需求与GDP空间相关性的组合预测模型

基于灰色理论的GM(1，1)模型[8]其本身具有明显的趋势，尽可能减少了人为假设对负荷预测带来的影响，更多的从电力系统及电力负荷本身的内在规律着手，对电力负荷的发展变化可以做出切合实际的分析.神经网络[9]在处理强非线性问题具有独到的优势，能够充分的考虑各种因素对所要处理的问题的影响，已被成功的应用于电力系统短期和中长期负荷预测中.空间自回归模型能够计及电力需求与影响因素的空间相关性，本文选用灰色GM(1，1)模型、BP神经网络及空间自会模型作为单个预测模型，利用Matlab优化工具箱对组合预测模型进行优化处理以得到最优结果，建立的模型如图1所示.

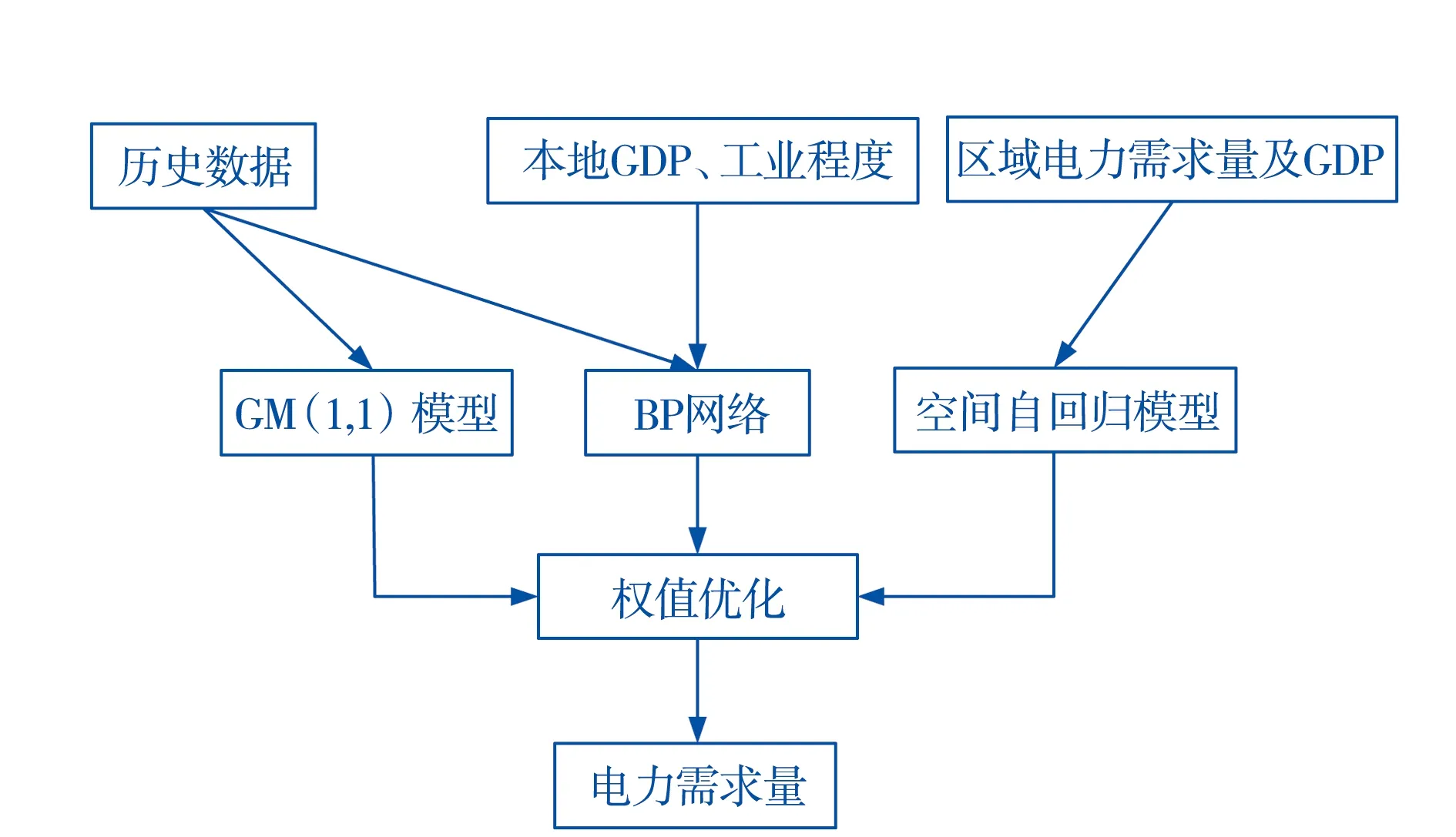
图1 组合预测框架图

3 应用实例

3.1 电力需求与GDP空间相关性分析

随着社会经济的高速发展，各省份之间的经济合作及劳动力转移，我国经济各区域之间的相互影响越来越显著.各区域之间的经济相互影响，相互促进发展.时间序列研究主要分析电力需求和经济增长之间的关系 ，没有考虑空间联系.而空间回归分析主要是研究电力需求和经济增长之间的空间关系.

根据全国(除西藏自治区和台湾省)空间相邻结构及《2017年中国统计年鉴》中数据，利用空间自回归模型对2006年各省(直辖市)用电与地区GDP之间的空间关系进行了分析.

线性回归及空间回归计算结果对比如表1所示.表1中，R2为复相关系数，用来表征自变量与因变量之间关系的密切程度.括号内为参数估计显著性检验统计量的p值.

表1 模型估计结果

对比表1中数据不难发现，普通回归模型与空间自回归模型的参数估计显著性检验统计量的p值均小于0.5，都在可接受的范围内，但空间自回归模型参数估计显著性检验统计量明显小于普通自回归模型，说明全国30个省、直辖市和自治区电力需求和地区生产总值GDP都有显著的空间相关特征，反映出邻近省、直辖市和自治区之间电力需求量和地区生产总值GDP具有明显的相似性.

表1中三种模型中，残差空间自回归模型的复相关系数最大，说明电力需求量存在“空间特性”，即各区域的用电量不仅与本区域的GDP有关，还与相邻区域的GDP存在空间上的联系.

同时根据利用空间相邻结构得到的空间权重矩阵绘制出电力需求量与GDP以及电力需求量与电力需求量之间的Moran散点图，如图2和图3所示.

图2中Moran’sI=0.398 1，数据点多集中于一、三象限，且分布图上直线为斜线，表明电力需求量与GDP之间在空间上具有较大的正相关性.而图3中Moran’sI=-0.013 1且数据点较为分散，表明用电量与用电量之间的空间相关性非常小.

3.3 电力需求量预测分析

电力需求量预测分析如表2所示.

表2 预测用数据

空间自回归模型分析表明，电力需求量与GDP之间存在较强的空间相关性，临近区域的GDP对本区域电力需求有一定影响.因此，在预测模型的建立过程中充分考虑了本地GDP、本区域工业化程度和空间区域GDP的影响，构建了图1所示的组合预测模型.

表3中数据为利用本文提出的模型和未计及空间相关性组合预测模对某省电网2006年和2007年电力需求量预测结果对比.预测过程中GDP及工业化程度分别采用了预测值和实际值.本文模型与未计及空间相关性组合预测模型预测结果误差对比柱状图(注：模型1即为本文模型，模型2为未计及空间相关性的组合预测模型)，如图4所示.由表3中数据和图4可以看出，两种预测模型中相关因素采用实际值的预测结果精度要高于采用预测值的精度.在实际预测过程中，相关因素同样是未知变量，而本文所建立的计及电力需求与GDP空间相关性的组合预测模型，相关因素采用预测值的预测结果仍高于相关因素采用实际值的未计及空间相关性组合预测模型预测结果，由此可见本文所建立的计及电力需求与GDP空间相关性的组合预测模型相对误差相对较小，适应性增强，预测精度完全满足生产和管理部门的需要，是一种行之有效的预测方法.

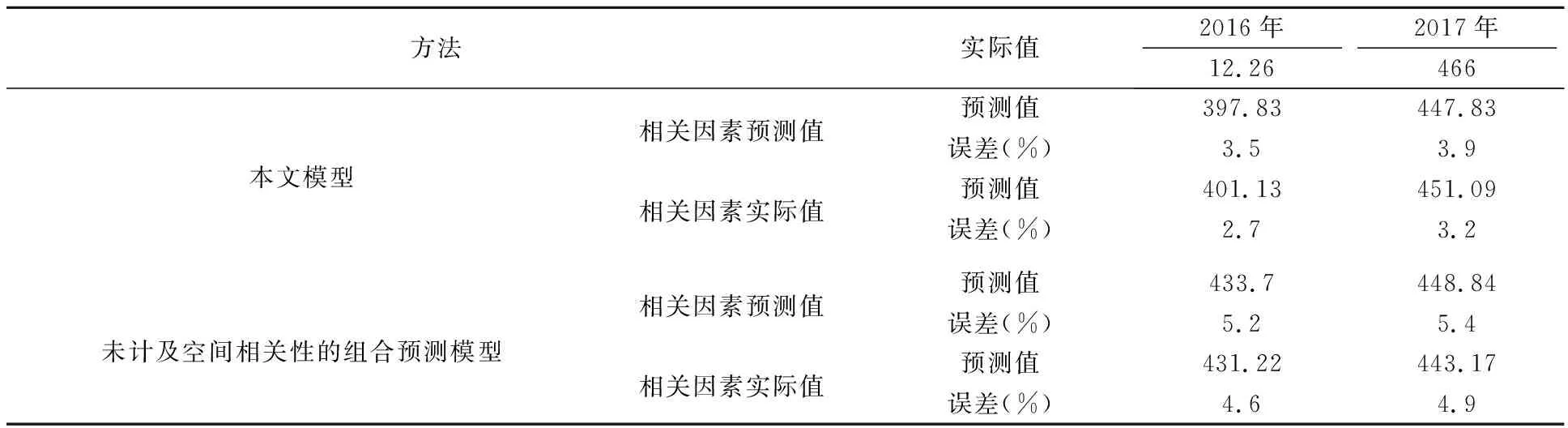
表3 预测结果

图4 预测误差对比图

4 结 论

本文利用空间自回归模型对电力需求量与GDP之间的空间相依性进行了计算分析，同时建立了基于空间自回归模型的计及空间相关性的组合预测模，实例分析结果表明：

(1)空间自回归模型的参数估计显著性检验说明全国30个省、直辖市和自治区电力需求和地区生产总值GDP 都有显著的空间相关特征，反映出邻近省、直辖市和自治区之间电力需求量和地区生产总值GDP 具有明显的相似性；

(2)空间自相关指数MoranI计算结果表明，电力需求量与GDP之间在空间上具有较大的正相关性；

(3)计及电力需求与GDP空间相关性的组合预测模型相对误差相对较小，适应性增强，是一种行之有效的预测方法.