420kA铝电解槽失电后热场分析及运用

孔凡成，徐建新

(1.昆明理工大学冶金与能源工程学院,云南 昆明 650093；2.云南云铝涌鑫铝业有限公司，云南 建水 654300)

从电解槽设计上来看，停电时间不能超过30 min以上.如果停电时间超过30 min以上，对铝解的正常生产和电解槽的结构都会产生不同程度的影响，极端的停电情况最终会导致电解槽濒临死亡[1-2].

有限元方法在铝电解槽电热场、磁场、应力场的研究中应用非常广泛.早在1971年，Haupin W E首先提出了一个计算电解槽槽膛内形的一维纯导热模型，通过应用该模型进行分析，得到了电解槽内各部的大概散热情况，同时估计了槽帮的厚度[3].Peacy、A.EK、Dupuis等也相继开展了电解槽的大量仿真研究，取得了许多突破性的成果[4-9].

国内梅炽、游旺、罗海岩、邓星球、张钦松、伍玉云、姜艳丽、徐于杰、王恒等在1992年到2016年间，针对铝电解槽的各个部件以及三维整槽模型进行仿真，通过仿真对电解槽各方面的改良提供了指导[10-18].

过去在电解槽热场的仿真模拟中，都是对运行槽进行仿真计算，没有针对失电后的电解槽进行仿真计算的案例，通过对失电后的热场进行仿真，获得失电后电解槽内介质的温度变化情况，以此给电解槽失电后的应急处置及平时的风险管理提供参考.基于此本文通过建立420 kA铝电解槽热传递模型，对其失电后的热量散失过程进行分析计算，分析其随停电时间的增加，整个电解槽内温度变化情况.

1 模型及方法

实际运用中的420 kA中间点式下料曲面阴极预焙槽横切面、纵切面图，如图1、图2所示.

1.2 模型建立

热场计算模型主要包括：阳极部分、阴极部分、电解质熔体、铝液、方钢、槽壳、保温材料等.本文将某实际应用中的400 kA铝电解槽作为分析对象.该420 kA槽长度为17.78 m、宽度为4.32 m，含48块阳极、48块阴极，阳极中缝宽度为180 mm，间缝宽度为30 mm.实际生产过程中铝水平均为33 cm，电解质水平平均为15 cm.全槽模型及网格划分如图3所示.

1.3 数学模型及定解条件

电解生产过程中，电解槽的热量来源主要是外部输入的直流电流在槽内产生的焦耳热，电解质的温度是控制在一个稳定的范围，所以电解槽内的热场符合含有内热源的稳态热传导方程：

(1)

公式中：t为温度；λX，λу，λz分别为三维各个方向的导热系数，与温度相关，W/(m·K)；Φ为由电流通过单位体积电解槽内的物料产生的焦耳热，对于不导电的材料Φ为0.

停电后电解槽失去了能量来源，此时电解槽符合没有内热源的三维非稳态热传导方程：

(2)

公式中：τ为时间，s；ρ为材料密度，kg/m3；c为比热容，W/(kg·K).

本次电解槽停电后散热过程的模拟，需要经历两个步骤：(1)建立稳态温度场分析模型；(2)利用稳态温度场模拟结果进行瞬态温度场模拟，其所涉及的定解条件如下：

初始条件：

(3)

第一类边界条件：

(4)

第三类边界条件：

(5)

公式中：T为节点温度，℃；T0为初始时刻温度，℃；Tf为给定温度值，℃；λ为导热系数W/(m·K)；n为换热表面的外法线.

第一类边界条件是指物体边界上的温度函数为已知；

第三类边界条件是指与物体相接触流体介质的温度和换热系数为已知.

1.4 热场边界条件

(1)电解槽周围温度按照车间实测平均温度施加为45 ℃，覆盖料表面平均温度施加为槽内烟气温度125 ℃，其余位置根据实测结果给出.

(2) 覆盖料与槽罩内空气的综合传热系数.

对流散热系数计算方法如下：

对流散热量Φ的计算公式为

Φ=Ak(Tf1-Tf2)，

(6)

公式中：k为对流换热系数，W/(m2℃)；k为环境温度，℃；Tf1为槽表面温度，℃；Tf2为环境温度，℃；A为散热面积，m2.

对流换热系数k使用有限空间自然对流传热的试验关联式进行计算，计算式如下：

(7)

公式中：Gr为格拉晓夫数；g为重力加速度，9.8 m/s2；αv为体胀系数，等于1/T；Th为壁面高温，℃；Tc为壁面低温，℃；δ为冷热两表面间的距离，m；ν为运动粘度，m2/s.

根据Gr的计算结果，确定努塞尔数Nu关联式如下：

Nu=0.061(GrδPr)1/3.

辐射散热系数计算方法如下：

覆盖料与槽罩内的辐射传热符合两个漫灰表面组成的封闭腔的辐射传热，其换热公式如下：

(8)

(9)

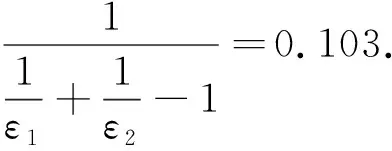
覆盖料与槽罩内的综合传热系数

K=K1+K2，

(10)

(3) 电解槽侧部槽壳外表面、方钢侧面及方钢头与周围环境的对流传热系数.

侧部槽壳、方钢侧面及方钢头对流散热符合大空间自然对流传热，其实验关联式为

Nu=C(GrPr)n，

(11)

公式中：常数C和系数n由Gr值确定.

(12)

根据公式(7)～公式(12)计算如表1所示.

表1 各个位置的对流系数

2 仿真结果分析及试验验证

2.1 温度场结果分析

(1)稳态温度云图与实际情况对比

稳态温度云图与实际情况对比，如图5、图6所示.

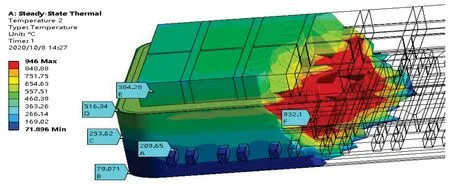
图5 稳态温度云图

图6 仿真结果与实际测量结果对比

从图6可以看出，仿真结果与实际测量结果存在一定的误差，但总的温度分布趋势是相互对应的，误差也在可接受的范围内，说明仿真结果具备可参考性.

从图7～图10可以看出槽壳、阴极、阳极的纵向温度分布以及方钢的横向温度分布均形成较大的温度梯度，其中温差最大的是方钢，温差达到848 ℃，温差最小的是阴极温差达到148 ℃.

(2)网格无关验证

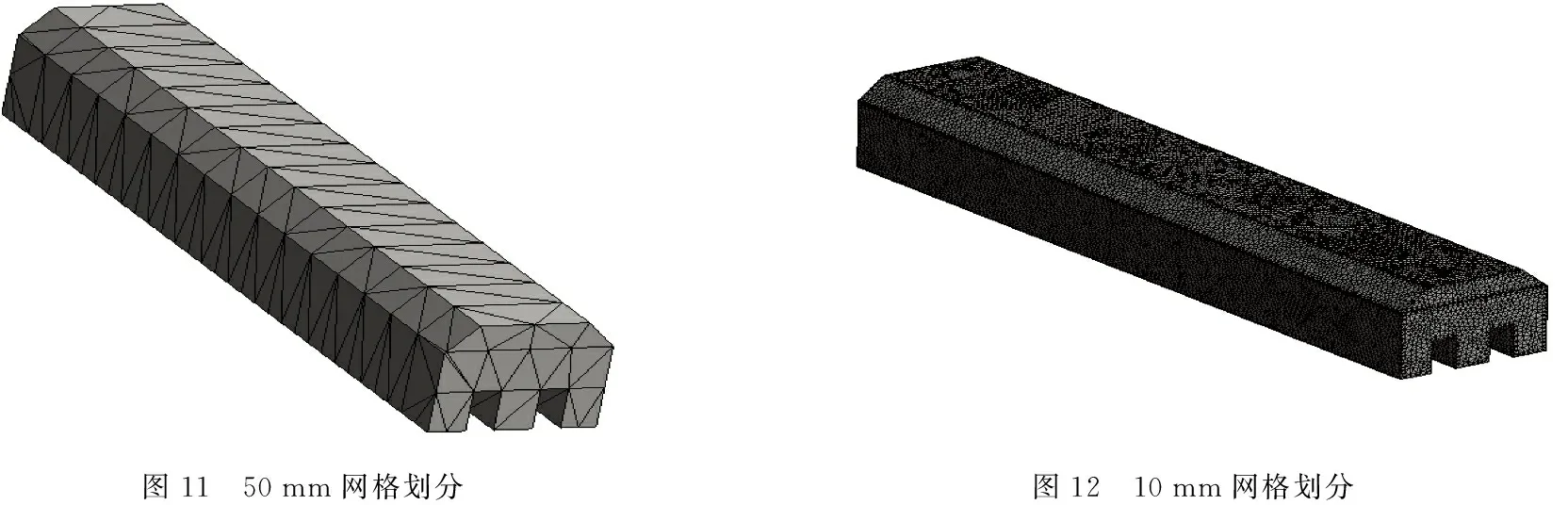
50 mm网格划分阴极温度云图如图9所示，与图13对比可以发现其温度差别非常微小，说明网格划分对结果影响较小.

图13 10 mm网格划分阴极温度云图

(3)30 min瞬态温度对比分析

从对比柱状图14中可以看出，停电30 min后，对比的5个温度点变化较小，最大温差存在于槽壳温度比对点D上，温差达到1.9 ℃，最大温度点下降6 ℃，有一定的温度降幅.

图14 失电30 min与稳态温度对比图

(4)2 h瞬态温度对比分析

从对比柱状图15中可以看出，停电2 h后，对比的5个温度点有明显的温度变化，最大温差存在于槽壳温度比对点C上，温差达到11.72 ℃，电解质F点的温度也下降了5.7 ℃，最大温度点下降9.62 ℃，降温明显，但B点温度依然无明显变化，说明槽底部保温效果较好.

图15 停电2 h与稳态温度对比图

(5)4 h瞬态温度分部图

图16 失电4 h后的温度云图

从对比柱状图17中可以看出，停电4 h后，对比的5个温度点温度变化较大，最大温差存在于槽壳温度比对点C上，温差达到16.39 ℃，电解质F点的温度下降了14.21 ℃，最大温度点下降19.08 ℃，电解质的温度已经落入了初晶温度范围内，B点温度下降依然较小，除B点外其余4个温度对比点的温度降幅均超过13 ℃.

图17 停电4 h与稳态温度对比图

(6)瞬态温度曲线变化分析

从图18可以看出，电解质和铝液的温度呈线性下降，阴极的温度并不是线性下降，温度下降的速度为u电解质>u铝液>u阴极，这是由槽内衬结构导致的，电解槽底部保温比电解槽上部保温要好，所以阴极的温度下降要缓慢的多.从图19可以看出阳极温度下降缓慢，槽壳温度下降速度明显大于阳极.

2.2 热通量分析

从图20～图22可以看出，电解槽槽壳两个侧面热通量最大，底部最小，槽壳侧面方钢以上的部分热通量比槽壳方钢以下的部分热通量要大一倍，槽壳总的热通量比阳极热通量要大27 509 W/m2，因此电解槽加强槽壳侧面保温，尤其是方钢以上侧面部分的保温，能够大幅降低电解槽的能量损失.

图20 整体热通量分布云图

2.3 失电后槽况分析

(1) 通过仿真结果可以看出，电解槽在停电30 min内，槽内介质温度变化较小，在3 ℃～5 ℃范围内，对电解槽在启动生产几乎没有影响；

(2) 电解槽停电2 h，槽内电解质温度下降约15 ℃左右，此时电解质温度已经达到初晶温度，电解质最大温度降低到929 ℃左右，对电解槽在启动生产会产生一定的影响，系列电流短时间不能达到正常生产的直流电流强度，需要通过2 h～3 h左右的能量平衡，才能够恢复到正常的直流电流强度，在恢复过程中电解槽效应频繁，导致功耗增加和能源浪费.

(3) 电解槽停电4 h，槽内电解质温度下降约20 ℃左右，电解质最大温度下降到915 ℃左右，铝液最大温度降低到918 ℃，最小温度下降到894 ℃左右，此时电解质收缩严重，铝液和电解质没有明显的边界层，此时启动电解槽难度较大，一方面电解质电阻较大，系列电流难以在短时间恢复到正常水平，另一方面在启动过程中可能发生由于电流分布不均匀导致阳极脱落的情况发生.

(4)电解槽停电8 h，槽内电解质温度下降到890 ℃，铝水温度下降到893 ℃左右，此时电解质完全下沉，铝液上翻，再次启动电解槽比较困难.

2.4 失电后经济损失分析

电解槽失电后通常会造成产量损失、电费损失、原料损失、人工损失、病槽死槽损失等.

(1)产量损失

失电后的产量损失通常可以按照下式计算：

(13)

公式中：W为损失的铝产量，t；I为电流强度，kA；L为电化当量，t.AL/KA通常取0.335 5；p为电流效率，通常取0.93；n为生产槽台数，视具体生产线而定；d为生产天数.

根据公式(13)，假设生产槽台数为200台，则停电30 min，损失铝产量为12吨，停电2 h损失铝产量为52吨铝，停电4 h损失铝产量108吨.若铝价格按14 000元/吨计算，则停电30 min损失168 000元，2 h损失728 000元，4 h损失15 12 000元.

(2)电费损失

恢复送电后，因失电时间长造成电解质电阻增大，运行电压较高，效应频发，造成大量电能浪费.

(3)材料损失

失电后的电解槽，当时间超过2 h电解质会有明显的收缩，恢复送电后为了恢复正常的生产工艺，需要投入比正常生产时更多的冰晶石、氟化盐等物料.

(4)病槽死槽损失

失电后在恢复生产时，电解槽极易形成病槽死槽，失电时间越长，形成病槽死槽的概率越大，重新修理一台420 kA的电解槽需要花费100万以上的费用.

3 结 论

本文通过建立420 kA铝电解槽全槽模型，应用Ansys软件进行了稳态温度场和瞬态温度场分析，得出的主要创新性结果有：

(1)建立了电解槽全槽稳态热场计算模型，重点计算了槽壳及覆盖料表面的对流散热系数.经过仿真分析，得到了电解槽失电前的温度分布、 散热量分布，并与实测结果进行了比较，发现仿真得到的温度分布与实测温度分布具有较好的一致性，证明了本文仿真模型及参数设置的合理性.同时通过对稳态温度场热通量分析发现电解槽整个槽壳侧面方钢以上的部分热量散失较为严重，加强槽壳侧面方钢以上部分的保温效果可以大幅度降低能量损耗.

(2)建立了电解槽瞬态热场计算模型，首次模拟了失电后随停电时间延长时间电解槽内各部件、各介质的温度变化情况.

基于仿真分析结果，在电解槽的风险管理中，30 min以内的停电事故属性一般性停电事故，2 h以上的停电事故属于较大事故，4 h以上停电事故属于重大停电事故.平时的风险管理中要做好风险分级管控，避免发生30 min以内停电事故，杜绝发生2 h以上的停电事故.