黎曼函数在数学分析反例教学中的应用

◎陈贤峰 (上海交通大学数学科学学院，上海 200240)

1 引 言

《数学分析》是高等院校数学与应用数学、信息与计算科学、统计学等专业必修的一门基础课程，对学生素质的训练和培养起着十分重要的作用.但由于其内容抽象，概念多，教学效果往往不太理想.对如何做好《数学分析》教学，文献[1-3]做了深入研究.笔者担任理科数学分析、工科数学分析主讲教师多年，深刻理解如何让学生真正“懂得”数学分析，其中反例教学是一个有效的抓手，通过记住几个特殊函数的性质，通过实例对几组重要数学概念进行对比，从而实现准确理解，并做到学以致用，黎曼函数是一个完美的实例.黎曼函数有着丰富的性质[4-6],本文将对此加以归纳和拓展，通过介绍黎曼函数在《数学分析》反例教学中的应用，发现各概念之间的差异，帮助学生更好地理解和应用相关概念.

2 黎曼函数是理解大学数学与中学数学研究对象不同的一个重要实例

中学阶段研究的函数都是初等函数，它的性质(奇偶性、周期性、单调性、有界性)及图形都比较简单，大学数学研究的函数比较抽象，很多性质无法直观展现，比如黎曼函数R(x)：

例1设

证明:f(x)在每一个点x上，它的值是有限的，但不是局部有界的(即在该点的任一邻域内是无界的).从而表明f(x)在R的任意子区间上是无界的.

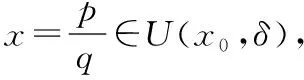
3 黎曼函数可以加强理解函数连续与可导之间的关系

函数的连续与可导从定义上看非常简单，但对初学者来说，容易从几何直观中得出一些结论，如函数一般都存在连续区间、总有可导点等等，但事实未必如此，例如，黎曼函数R(x)有无数个连续点(无理点处都连续)，但不存在连续区间，同时没有一个可导点，即处处不可导.若将黎曼函数改造为前面的f(x)，可得到一个处处不连续、处处不可导的函数.

例2证明R(x)在[0,1]上处处不可导.

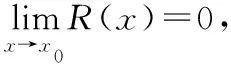
设x0∈(0,1)为无理点，考虑

于是

更进一步，存在这样一个处处连续、处处不可导函数的例子[7]，处处不可导的证明与本题类似.

4 黎曼函数可以加深理解处处取得极值函数与常值函数的联系与区别

极值是数学分析中很重要的概念，在实际应用中经常出现，它表示函数在一点附近局部最高或局部最低.学生在学习中会有一个疑问：处处取得极值函数是不是一定是常值函数？黎曼函数给出了回答.

例3黎曼函数R(x)在R上处处取得极值，在有理点处取得严格极大值，在无理点处取得极小值.

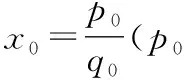
任取无理数x0，则对∀x∈R，R(x0)=0≤R(x)，表明x0为R(x)的极小值点.

注 可以证明：一个定义在R上的函数，如果处处取极大值或处处取极小值，它是一个常值函数.

5 黎曼函数是理解不定积分与定积分联系与区别的一个好例子

函数黎曼可积性是《数学分析》学习中的一个难点，一般教材中都谈到常见的三类可积函数：闭区间上的连续函数，仅有有限个间断点的有界函数，闭区间上的单调函数，结论比较直观，函数图形都可以想象，但可积函数类还有很多，有些图形无法想象，比如黎曼函数，它有无穷个间断点，图形也画不出来，但黎曼函数在[0,1]上是黎曼可积的.下面给出证明：

例4证明R(x)在[0,1]上黎曼可积.

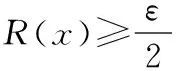
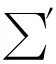
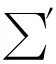
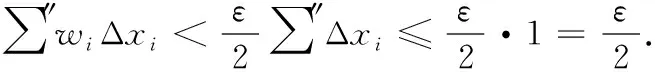
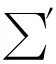
由函数可积性充要条件[8]知，R(x)在[0,1]上定积分存在.

注1 黎曼函数在[0,1]上可积性是勒贝格定理[9]最好的应用实例.

注3 连续函数的复合是连续函数，可导函数的复合是可导函数，但是可积函数的复合却未必是可积函数，下面利用黎曼函数，构造反例如下：

令

由于f(x)在[0,1]上只有一个间断点且有界，故f(x)在[0,1]上可积，注意到复合函数

由迪利克雷函数在[0,1]上不可积，知复合函数f(g(x))不是可积的.

6 结 论

《数学分析》概念抽象，通过利用黎曼函数，采用反例教学法，加强对概念之间的联系与区别的分析，达到准确掌握和熟练应用的效果.