在动态演示中发展空间观念

黄娟

学习“角”的相关知识对于培养学生的观察能力、实践操作能力，发展学生的空间观念和度量思维等有重要作用。如何帮助学生发现角、认识角，会用量角器度量角、画出角，利用多种方法比较角的大小呢？本期，我们讨论如何更好地帮助学生学习角的相关知识。

“角的分类”是人教版四年级上册第三单元《角的度量》中的例2。本课时在学生学习了《角的认识》的基础上，引导学生通过测量、动态演示、自主体验完善“角”的概念，形成特殊角的定义，厘清不同角之间的关系，发展学生的空间观念。

一、借助转换，完善“角”的概念

四年级学生对锐角、直角和钝角的认识是基于直观层面的，主要以一副三角尺上的直角作为工具来研究。因此，笔者以直角为突破口，引导学生从直观认识角转换到利用度数来定义角，完善学生对直角、锐角和钝角的认识，发展学生的空间观念。

上课伊始，笔者让学生回顾量角的步骤，然后用量角器量出三角尺上直角的度数。通过测量，学生知道直角等于90°。把直角的概念从直观认识过渡到度数来定义，使学生进一步认识了直角。接着，笔者引导学生回顾“角”的概念：从一点引出的两条射线所组成的图形叫作角。这是直观静态层面上“角”的概念，其实“角”的概念还可以延伸到动态层面上来，即“角可以看作由一条射线绕着它的端点，从一个位置旋转到另一个位置所形成的图形”。直角可理解为：由一条射线绕着它的端点旋转90°后形成的图形（多媒体动态演示）。

随后，笔者设疑：“直角三角尺上其他角是多少度？又是怎样形成的呢？”学生回答：直角三角尺上的其他角可以是30°、45°、60°，分别是由一条射线绕着它的端点旋转30°、45°、60°后形成的。笔者反问：“我们刚才研究了直角和锐角的形成过程。钝角又是怎样形成的呢？它的度数又会是多少呢？”学生回答：钝角也可以看成是由一条射线绕着它的端点旋转比90°大比180°小的角后形成的图形（多媒体动态演示钝角的形成过程）。

从测量三角尺上各个角的度数入手，一方面利用学生已有的认识经验，另一方面也比较直观，有说服力。在研究过程中，以角的动态形式，将直观层面上的概念上升到度量层面上来定义，既完善了锐角、直角和钝角的概念，沟通这三类角的关系，又提升了学生原有的认知水平，为后续研究平角和周角做铺垫。

二、借助演示，形成特殊角的定义

空间观念是在空间知觉的基础上形成的，空间观念的积累可以促进空间想象力的形成。基于这一点，教学中，笔者引导学生在动态演示角的形成的过程中获取动态层面上角的知识，形成初步的空间观念。

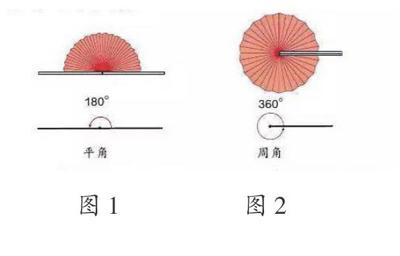
平角和周角是本课时新认识的两种角，用已有的经验，借助角的动态定义，容易引出这两个角的定义。笔者继续引导学生观察动态的180°角的形成过程（如图1）。

师：此时形成的角有什么特点？两条射线的状态是怎样的？

生1：两条射线变成了一条直线。这时形成的角是180°的角。

生2：这是一个最大的钝角，这个角有两个直角大。

师：当一条射线绕着它的端点旋转180°后，它已经不是钝角了。它有一个新的名称叫作平角。请同学们观察，从图中我们可以知道怎样的角是平角？平角等于多少度？

生3：一条射线绕着它的端点旋转半周形成的角叫作平角，平角等于180°。

师：说得很好，平角的始边和终边在同一条直线上。但是平角与直线是有本质区别的，平角是一个角，能够度量，而直线是一条线，不能度量;最明显的区别是平角有一个端点和两条射线，而直线没有。下面请同学们画一个平角，并说说画平角时应该注意什么？

生4：先确定顶点，然后过这一点，在同一直线上画两条射线，再标明角的符号及角的度数。

师：如图2，同学们再想一想，把一条射线绕着它的端点旋转一周后得到的图形，还是不是一个角呢？

生5：一条射线绕着它的端点旋转一周后与另一条射线重合了，就变成了一条射线，不是角了。

生6：不对，这个图形是一个角，因为它有一个顶点和两条射线，只不过这两条射线重合了。

师：对，这个图形是一条射线绕着它的端点旋转了一周，也就是360°，这个角叫作周角，周角等于360°。你能画出一个周角吗？画周角时应注意什么？

生7：先画角的顶点，再过点画一条射线。画周角时要注意标上角的符号和角的度数。

经历了这一活动，学生不仅对两种特殊角形成了完整的定义，而且提升了学生的空间想象力。

三、借助体验，厘清“五类角”的关系

自主体验要求学生参与知识形成的过程，即利用已有的知识与经验获取新知识的过程。“角的分类”实质就是通过“分”，引导学生在了解直角、锐角、钝角的度数的基础上，认识两种新的角——平角和周角。所以笔者引导学生自主体验，借助角的度数这一要素，明晰这五类角的关系。

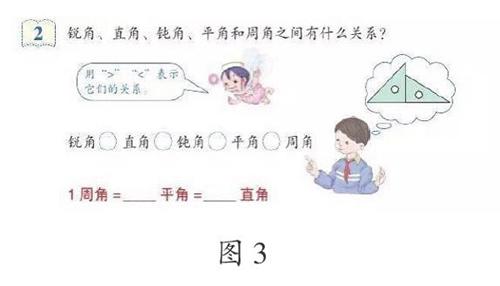
首先，笔者呈現第42页的例2（如图3）。

学生理解了例2后，笔者先要求学生以小组为单位，根据角的度数的特点，结合画角时的体会，感知这五种角的大小，表示出它们之间的关系。接着，让学生用三角尺摆出不同的角，体会不同角的度数差异，特别是锐角、钝角的再认识，使学生进一步明确：锐角的度数范围是“0°<锐角<90°”;钝角的度数范围是“90°<钝角<180°”。然后，让学生体会周角与0度角的区别。0度角一方面是由有共同端点，且重合的两条射线组成的图形，这时角的两边不分始边和终边;另一方面是一条射线绕着端点旋转0度后形成的图形，实际上没有旋转，这时角的终边就是始边。而周角是一条射线绕着它的端点旋转了360°后形成的角，实际上旋转了一周，周角的终边和始边重合。

最后，让学生在已有的认知基础上，完成下表。

锐角、直角、钝角、平角、周角之间的关系

学生经历了自主探索，不仅对这五类角的特征有了进一步的认知，而且厘清了这五类角之间的关系，强化了对角的概念的系统认知。

（作者单位：应城市实验小学）

责任编辑  张敏