Cooperative behaviors of coupled nonidentical oscillators with the same equilibrium points∗

Wen Sun(孙文) Biwen Li(李必文) Wanli Guo(郭万里)Zhigang Zheng(郑志刚) and Shihua Chen(陈士华)

1School of Mathematics and Statistics,Hubei Normal University,Huangshi 435002,China

2School of Mathematics and Physics,China University of Geosciences,Wuhan 430074,China

3College of Information Science and Engineering,Huaqiao University,Xiamen 361021,China

4College of Mathematics and Statistics,Wuhan University,Wuhan 430072,China

Keywords: amplitude death,bounded chaotic synchronization,mismatched parameter

1. Introduction

Due to potential applications in biological and social systems, coupled identical oscillators have received much attention recently.[1,2]The vibration behavior is a common phenomenon appearing in them and is useful for fault diagnosis.[3,4]In addition to this,lots of cooperative phenomena such as complete synchronization (CS), amplitude death(AD), and oscillation death (OD) happen on account of their interactions with other oscillators.[5–8]CS means the complete coincidence of the states of all oscillators no matter what the states will be, which appears only if the interacting oscillators are identical.[9–11]If the oscillators cannot achieve CS by themselves, various approaches such as linear feedback control,[12–15]adaptive control,[16–19]pinning control,[20–23]time-triggered impulsive control,[24–26]event-triggered impulsive control,[27,28]and sampled control[29]have been put forward to guide all the oscillators to reach the desired goal.AD refers to a coupling-induced suppression of oscillating by stabilizing an existing homogeneous steady state.[30]It is a special form of complete synchronization, that is, not only the states of all oscillators are coincident, but also the amplitudes of all oscillators are zero. Yamaguchi and Shimizu considered Kuramoto oscillators and found that sufficiently strong coupling and sufficient wide distribution of natural frequencies are needed for amplitude death to be stable.[31]Since amplitude death corresponds to the cessation of rhythmicity in a system and may be relevant to certain pathology of biological oscillators, it has drawn greater attention.Mirollo and Strogatz analyzed an array of coupled limitcycle oscillators with mean-field coupling and randomly distributed natural frequencies,found the conditions that the system underwent amplitude death, and determined the region for which amplitude death was stable.[32]Atay studied amplitude death phenomenon theoretically in distributed timedelay.[33]Prasad found that amplitude death can occur in identical as well nonidentical coupled chaotic systems by delayed coupling.[34,35]Liu and Yang discovered the partial amplitude death in coupled chaotic oscillators when the interaction was strong enough.[36,37]Kruths analyzed the mechanisms of amplitude versus oscillation death in oscillation quenching.[38]Different from AD,OD is characterized by a newly born inhomogeneous steady state. It has been reported that CS(including AD)is impossible except that the nonidentical oscillators have the same equilibrium points.[39]

The rest of the paper is organized as follows. In Section 2, we present our considered model. In Section 3, we demonstrate amplitude death and bounded chaotic synchronization of two coupled nonidentical oscillators with different coupling modes and coupling strength. Finally, a brief summary is made in Section 4.

2. Theoretical analysis and experimental results

The isolated Lorenz oscillator is described as

Fig.1. The two largest Lyapunov exponents versus parameter a for a single Lorenz system.

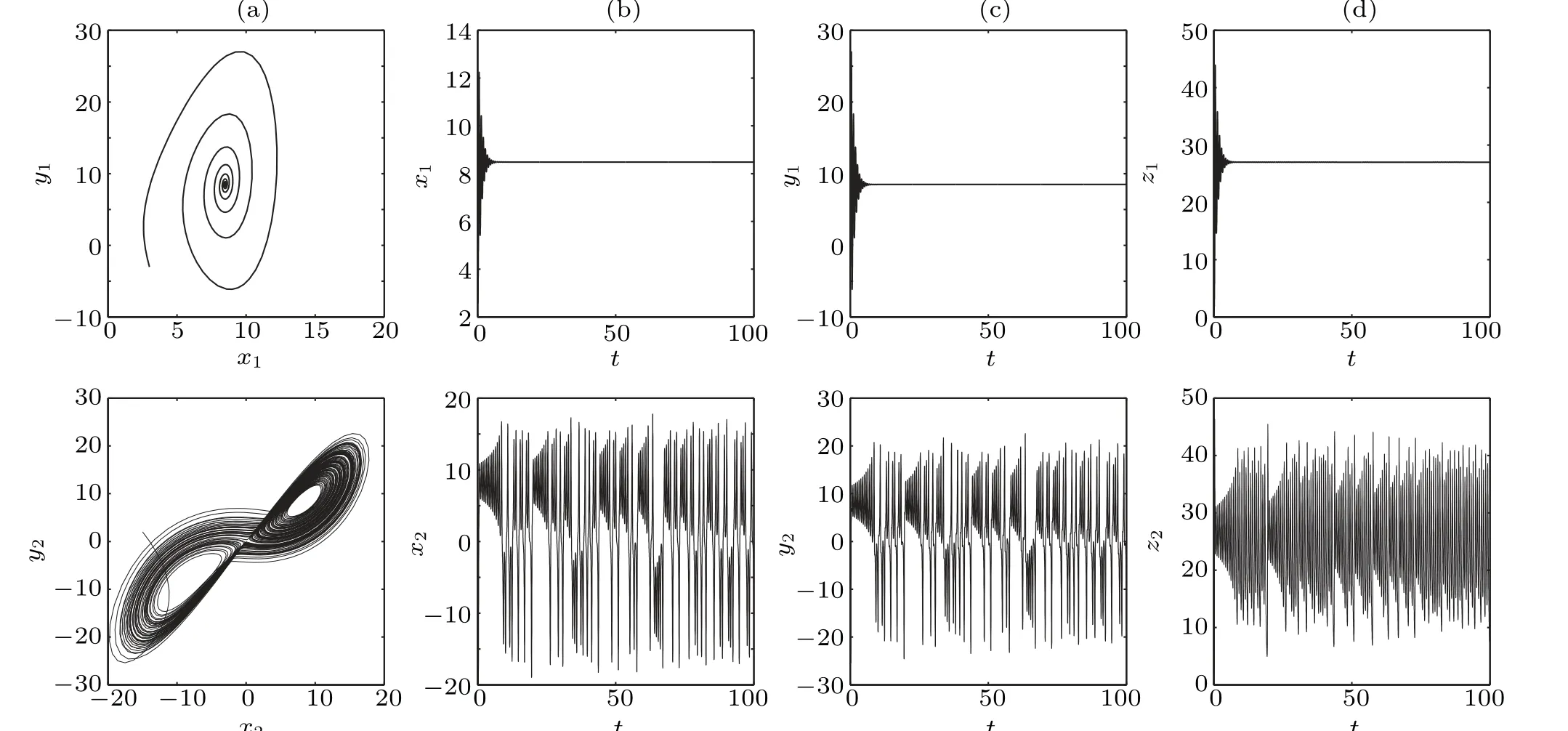
Fig.2. The dynamics of two uncoupled oscillators with initial value(3,−3,1,15,2,3). (a)The phase portraits in the x–y plane. (b)The time sequence of x. (c)The time sequence of y. (d)The time sequence of z. The top are for the oscillator 1 and the bottom for the oscillator 2.

Two coupled Lorenz oscillators can be described by

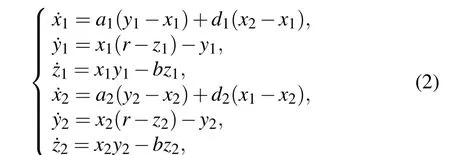
wherea1=1 anda2=12 are mismatched parameters.d1,2are the coupling strengths. In the absence of coupling, oscillator 1 is unchaotic, and its trajectories converge to its fixed pointsP+orP−depending on the initial condition;while oscillator 2 displays chaotic motion for the same initial value(3,−3,1,15,2,3),which can be seen from Fig.2.

For convenience,Eq.(2)can be written as

fork1>0,k2>0,ε1>0,ε2>0,X1,X2,Y1,Y2∈Rnandt>0.

This assumption is moderate, and many chaotic systems such as Chua’s oscillators, R¨ossler systems, Lorenz systems,Chen systems,and L¨u systems satisfy this assumption.

2.1. Unidirectional couplings

(I)Whiled1/=0,d2=0,the chaotic oscillator is the drive system,while the nonchaotic oscillator is the response system,Eq.(2)is turned into

Figure 3 illustrates the two largest Lyapunov exponents versus the coupling strengthd1,in which the first-largest Lyapunov exponent is positive while the second-largest Lyapunov exponent is zero withd1increasing. Figure 4 shows the phase portraits in thex–yplane for two unidirectional coupled oscillators with the coupling strengthd1=20 in (a) and the time sequences ofx,y,zin(b), (c)and(d). It is clear that the unchaotic oscillator 1 can synchronize to the chaotic trajectories of oscillator 2. Bounded chaotic synchronization (BCS) occurs.

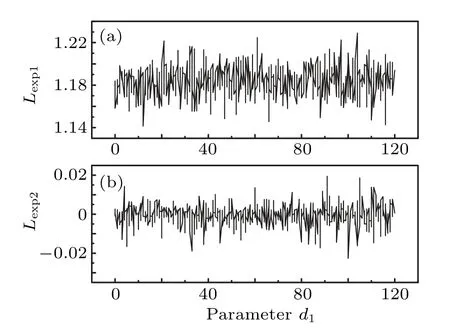
Fig. 3. The two largest Lyapunov exponents versus the coupling strength d1 (d2=0)for two unidirectional coupled oscillators.

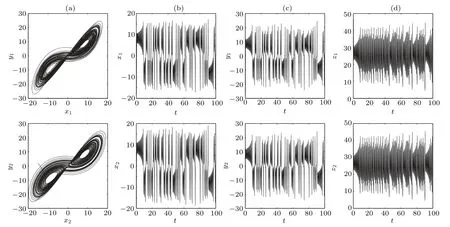
Fig.4. The dynamics of two unidirectional coupled oscillators with the coupling strength d1=20(d2=0)and initial value(3,−3,1,15,2,3).(a)The phase portraits in the x–y plane. (b)The time sequence of x. (c)The time sequence of y. (d)The time sequence of z.

(II)Whend1=0,d2/=0,the chaotic oscillator is the response system,while the nonchaotic oscillator is the drive system,Eq.(2)is changed into

Ifk2−d2≤0,then ˙V(e(t))≤−ε2‖e(t)‖2. We getV(e(t))≤V(e(0))e−2ε2t. Thus,e(t)→0 and amplitude death occurs.

Figure 5 illustrates the two largest Lyapunov exponents versus the coupling strengthd2, in which the first-largest and the second-largest Lyapunov exponents are negative as the coupling strengthd2increases. Under the drive of oscillator 1, the chaotic oscillator 2 can evolve into one of two fixed points of oscillator 1 depending on the initial condition and does not run away since that is also its own equilibrium point.Namely, amplitude death appears. Figure 6 shows the phase portraits in thex–yplane for two unidirectional coupled oscillators with the coupling strengthd2=30 in (a) and the time sequences of the variablex,y,zin(b),(c)and(d).

In the unidirectional coupled non-identical oscillators,the response system can synchronize to the drive system even with mismatched parameters. Different synchronization pattern of BS is mainly regulated by the strength and the directivity of the couplingd1(d2).

Fig. 5. The two largest Lyapunov exponents versus the coupling strength d2 (d1=0)for two unidirectional coupled oscillators.

When the couplings are undirected or directed, theoretical analysis similar to the above is very difficult due to the heterogeneity of nonidentical oscillators. However,we get some interesting numerical results.

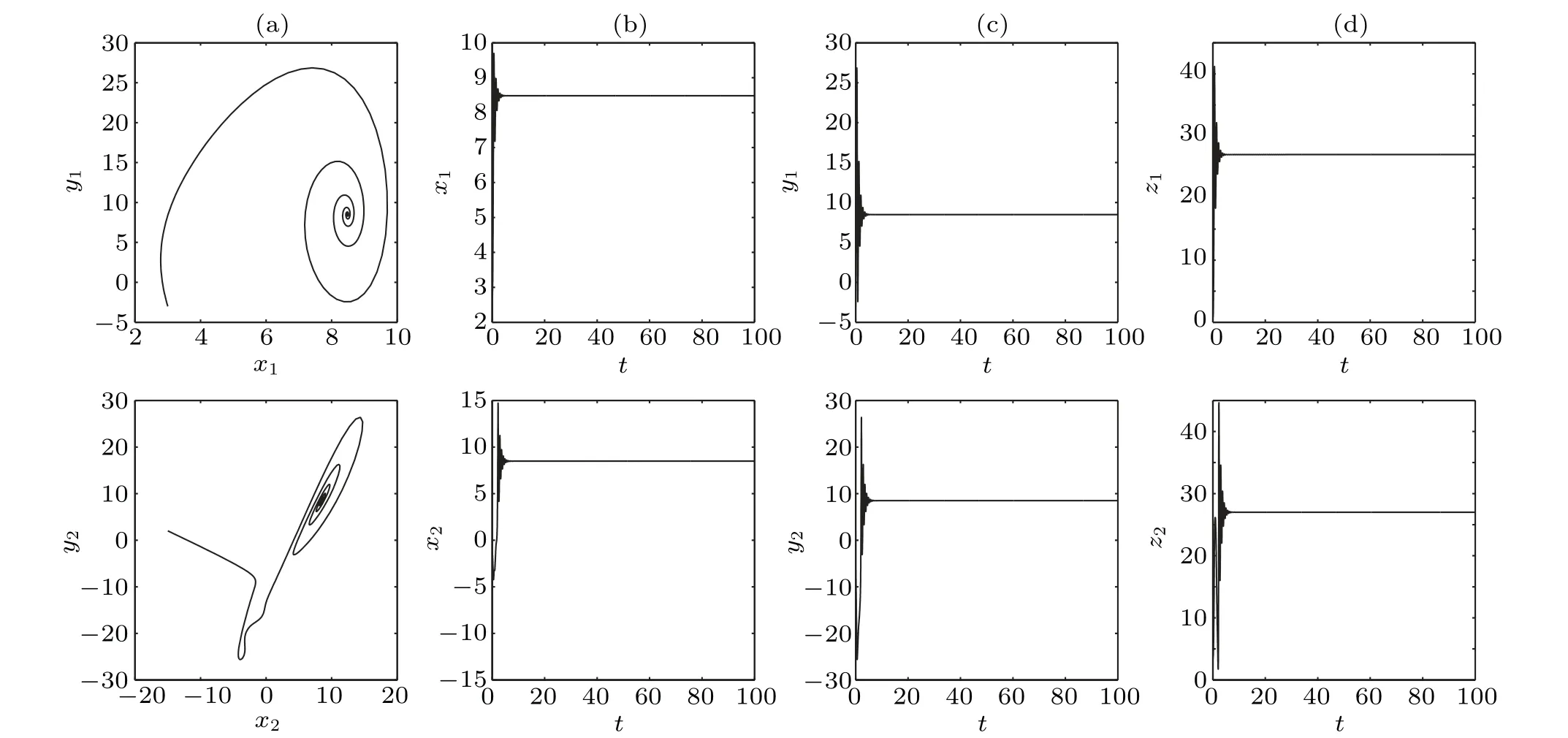
Fig.6. The dynamics of two unidirectional coupled oscillators with the coupling strength d2=20(d1=0)and initial value(3,−3,1,15,2,3).(a)The phase portraits in the x–y plane. (b)The time sequence of x. (c)The time sequence of y. (d)The time sequence of z.

2.2. Undirected couplings

When the coupling is undirected,the dynamics of the coupled oscillators are more complex and controlled by the coupling strengthd. As the coupling strength increases,some intriguing new phenomena can occur. The two largest Lyapunov exponents versus the coupling strengthdare plotted in Fig.7.

Fig.7. The two largest Lyapunov exponents versus the coupling strength d for two undirected coupled Lorenz systems.

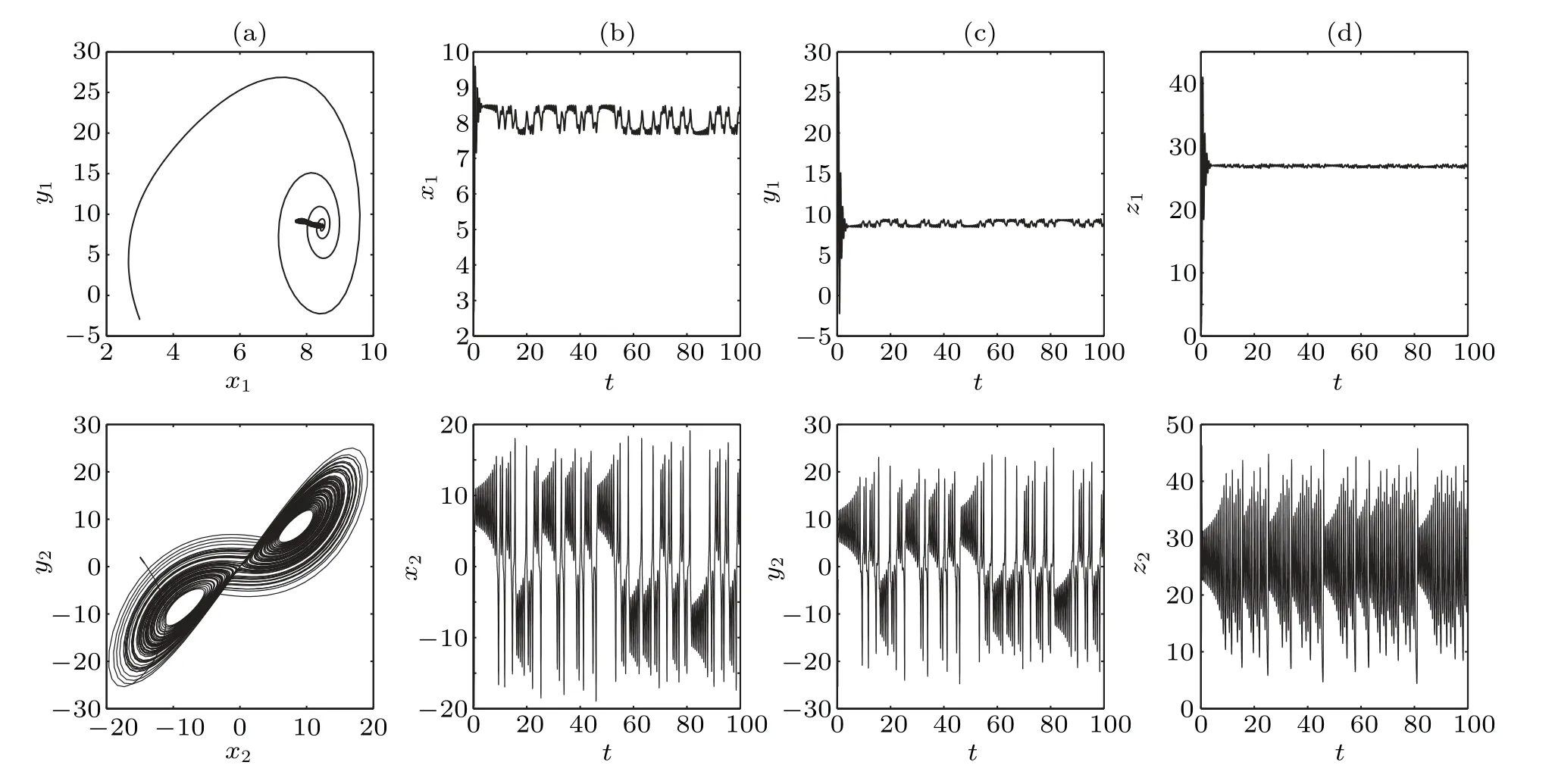
Fig. 8. The dynamics of two undirected coupled oscillators with the coupling strength d =0.1 and initial value (3,−3,1,15,2,3). (a) The phase portraits in the x–y plane. (b)The time sequence of x. (c)The time sequence of y. (d)The time sequence of z.

To get more information about the dynamical behaviors implicit in Fig. 7, we depict the phase portraits and the time sequences ofx,y, andz. As the coupling between the oscillators is turned on, especially the coupling strengthdis very small, the interaction between them is not enough to change their dynamics much. Oscillator 1 oscillates near its equilibrium point,while oscillator 2 oscillates near its chaotic trajectories. Figure 8 shows the phase portraits in thex–yplane for two undirected coupled oscillators withd=0.1 in(a)and the time sequences ofx,y,zin(b),(c)and(d).

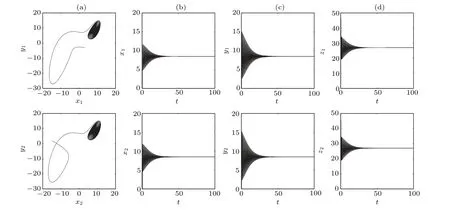
Fig.9. The dynamics of two undirected coupled oscillators with the coupling strength d=20 and initial value(3,−3,1,15,2,3). (a)The phase portraits in the x–y plane. (b)The time sequence of x. (c)The time sequence of y. (d)The time sequence of z.

Fig. 10. The dynamics of two undirected coupled oscillators with the coupling strength d =42 and initial value (3,−3,1,15,2,3). (a) The phase portraits in the x–y plane. (b)The time sequence of x. (c)The time sequence of y. (d)The time sequence of z.

When the coupling strengthdgoes beyond a critical coupling strengthd02,oscillator 1 can be pulled to the chaotic trajectories of oscillator 2. Figure 10 shows the phase portraits in thex–yplane for two undirected coupled oscillators withd=42 in(a)and the time sequences ofx,y,zin(b), (c)and(d). Interestingly enough,the AD states of oscillator 1 are revived again by the coupling and become chaotic attractors.

2.3. Directed couplings

When the coupling is directed and weighted,the dynamics of the coupled oscillators are regulated by two coupling strengthsd1andd2. The two largest Lyapunov exponents versus the coupling strengthd1andd2are plotted in Fig. 11,where the two largest Lyapunov exponents are negative in the blue area and positive in the gray area. We find that different cooperative behaviors of two coupled oscillators with mismatched parameters emerge according to the variation ofd1andd2. In the blue lower triangular overlapping region in Figs. 11(a) and 11(b), the non-chaotic synchronization, i.e.,amplitude death happens. In the other regions, the bounded chaotic synchronization takes place, resulting in the oscillators oscillating.

When we putd1=20 andd2=4 in the bounded chaotic synchronization region (the gray areas in Fig. 11(a) and the blue areas in Fig.11(b)),where the first-largest Lyapunov exponent is positive while the second-largest Lyapunov exponent is negative,bounded chaotic synchronization occurs.Figure 12 shows the phase portraits in thex–yplane for two directed and weighted coupled oscillators in (a) and the time sequences ofx,y,zin(b),(c)and(d),which are in agreement with Fig.11.

When we putd1=4 andd2=16 in the amplitude death region (the blue areas in Figs. 11(a) and 11(b)) where the two largest Lyapunov exponents are negative,amplitude death takes place. Figure 13 shows the phase portraits in thex–yplane for two directed and weighted coupled oscillators in(a)and the time sequences ofx,y,zin(b),(c)and(d).

The above analysis concludes that the coupling strengthd1is intended for oscillating, while the coupling strengthd2is valid for converging. Thus, there is a trade-off between making oscillators oscillate and making them convergent. The competition between the coupling strengthd1andd2is the critical factor that induced these transitions between amplitude death and bounded chaotic synchronization.

Fig. 11. The two largest Lyapunov exponents versus the variation of d1,d2 for two directed and weighted coupled Lorenz systems. (a)The first-largest Lyapunov exponent. (b) The second-largest Lyapunov exponent.

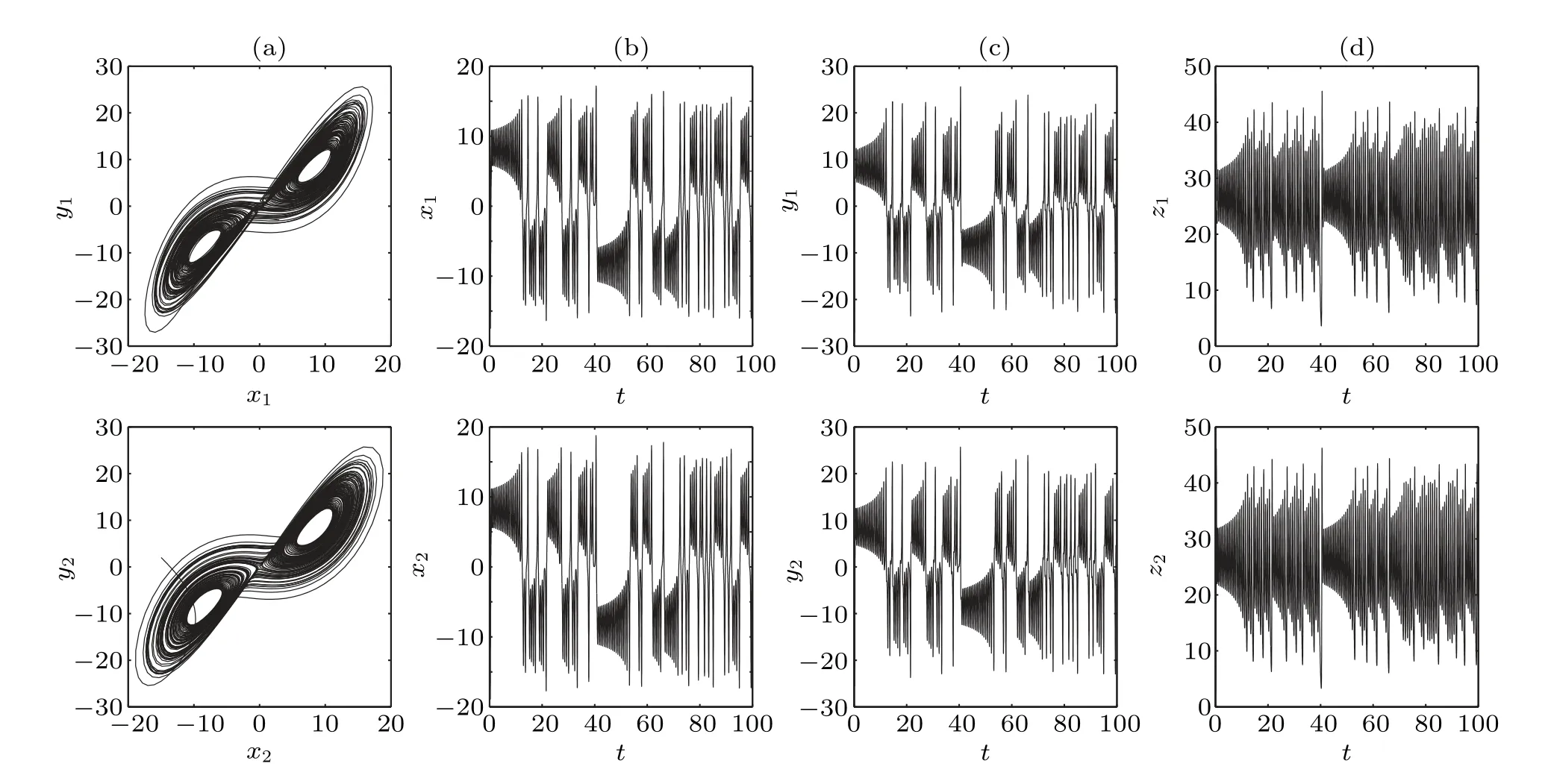
Fig.12. The dynamics of two directed and weighted coupled oscillators with d1=20,d2=4 and initial value(3,−3,1,15,2,3). (a)The phase portraits in the x–y plane. (b)The time sequence of x. (c)The time sequence of y. (d)The time sequence of z.

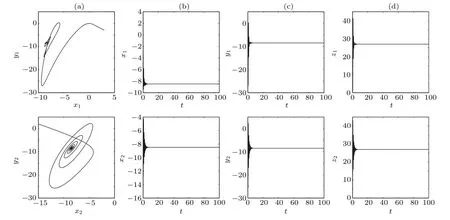
Fig.13. The dynamics of two directed and weighted coupled oscillators with d1=4,d2=16 and initial value(3,−3,1,15,2,3). (a)The phase portraits in the x–y plane. (b)The time sequence of x. (c)The time sequence of y. (d)The time sequence of z.

3. Conclusions

We have investigated the cooperative behaviors of coupled nonidentical oscillators with the same equilibrium points,where one oscillator is convergent while the other is chaotic.We find that when the coupling is unidirectional,the responding system can easily synchronize to the driving system with the coupling strength increasing. When the coupling is undirected, it can bring the coupled oscillators to different cooperative behaviors. Specifically, the non-chaotic synchronization,including amplitude death and the existence of death intervals,occurs as the interaction is strong;while the coupling is beyond a certain threshold, bounded chaotic synchronization takes place.In the case of directed and weighted coupling,amplitude death islands appear in two-parameter spaces. Our next concern is how to use our proposed methods to revive or cease the rhythmicity of certain biological oscillators, which is helpful for the recovery of some diseases.