基于因果分解的SOFC系统故障根源诊断方法

陈孟婷，付晓薇*，樊 洋，李 曦

(1.武汉科技大学 计算机科学与技术学院，湖北 武汉 430065； 2.智能信息处理与实时工业系统湖北省重点实验室，湖北 武汉 430065； 3.华中科技大学 人工智能与自动化学院，湖北 武汉 430074)

0 引 言

固体氧化物燃料电池(solid oxide fuel cell，SOFC)作为最有潜力的替代能源之一，在军事、交通、家用等领域有着广阔的应用前景[1]。目前，华中科技大学已完成千瓦级独立发电系统的发电与示范运行，但仍存在系统故障引起的输出电力波动问题[2]，系统的稳定运行仍面临着巨大挑战。因此，设计一种SOFC系统故障根源诊断方案，辅助现场人员查明故障原因显得尤为重要[3-5]。

目前，故障根源诊断问题常用的方法包括：谱包络[6]、邻接矩阵[7]、格兰杰因果分析[8]、传递熵[9]和贝叶斯网络[10]等。考虑到工业过程[11-12]和SOFC系统都属于多变量强耦合系统，借鉴上述振荡识别方案，应用过程数据驱动的因果分析方法实现SOFC系统故障根源诊断具有较好的实用价值。

文中针对SOFC系统发电过程中普遍存在的时变、非线性和非平稳性故障现象，对因果分析方法进行深入探讨，提出了一种基于因果分解的故障根源诊断方法。

1 基于因果分解的故障根源诊断方法

1.1 基于瞬时相位相关性的因果关系分析

文中引入瞬时相位相关性概念评估因果关系。该方法在考虑时间优先原则的同时，强调因果交互作用的瞬时关系，从而避免了预测因果关系方法中的时滞限制。

已知任意两个信号S1(t)和S2(t)间的瞬时相位差可以简单表示为Δφ12(t)=φ2(t)-φ1(t)。当信号间高度相关时，则相位差是恒定的；否则，相位差随时间波动很大。定义瞬时相位相关性Coh[13]：

(1)

式中，被积函数eiΔφ12(t)是复平面上单位长度的矢量，指向与x轴正方向形成角度为Δφ12j(t)的方向。当瞬时相位差在整个信号上变化很小时，Coh值接近1；而当相位差随时间显著变化，意味着存在一组指向所有可能方向的向量，则Coh趋于0。

在基于瞬时相位相关性的因果关系分析中，S1(t)和S2(t)间的因果交互被编码为瞬时相位相关性。当因果相关的固有成分从“果”信号中移除时，瞬时相位相关性被减弱，可以表示为：

(2)

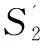
1.2 过程变量间的因果分解

集成经验模态分解(ensemble-empirical mode decomposition，EEMD)算法[14]适用于非线性、非平稳过程数据。根据原始信号的极大极小值的谱包络线，将信号分解成有限个固有模态函数(intrinsic mode function，IMF)。通过EEMD分解过程数据并测量对应IMF之间的瞬时相位相关性，实现过程变量间的因果分解。

对于S1(t)和S2(t)中的任意一对IMF组，S1j(t)和S2j(t)可以表示如下：

S1j(t)=A1j(t)cosφ1j(t)

(3)

S2j(t)的计算同上。式中，瞬时幅值A1j(t)和瞬时相位φ1j(t)经Hilbert变换[15]后计算得到：

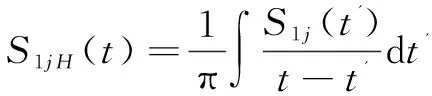
(4)

(5)

(6)

S2jH(t)、A2j(t)和φ2j(t)的计算同上。

由于存在部分IMF分量的相位动态变化受到“因”过程变量的影响，当从“果”变量中移除该IMF分量，并重组再分解得到一组新的IMF集，使得相位动态特性重新分配到相应IMF时间尺度上。由于引起效果的相位动态特性是“因”变量所固有的，重组再分解的新时间序列保留其他IMF的相位动态特性，仍会影响结果时间序列的相位动态变化，移除对应IMF前后的瞬时相位相关性测量值差别不大。

为此，分解和重组再分解过程可以量化多过程数据的因果差异。

利用方差加权欧氏距离量化S1和S2在第j组IMF分量中的因果作用程度：

(7)

式中，β的取值范围在(0,1)，S1j与S2j的因果作用方向取决于DS1j→S2j和DS2j→S1j中值较大者。

1.3 算法流程

文中方法主要流程如下：

步骤 1：分解过程变量，并确定变量两两间在各IMF分量下的瞬时相位相关性；

步骤 2：依次移除变量的IMF，执行重组再分解生成新IMF集，计算该变量与其他变量间移除IMF分量下的瞬时相位相关性；

步骤 3：通过估计从原变量间的相位相关性到重组变量间的相位相关性偏差以确定因果强度。

2 SOFC系统实验验证结果

在本实验中，采用了华中科技大学千瓦级带水蒸气重整SOFC系统来阐述文中所提出的故障根源诊断方法的有效性。

该系统由五个组件构成：空气与燃料供给、换热器、重整器、SOFC电堆、燃烧室。实际发电过程中，甲烷和水蒸气通入重整器，经重整反应后得到的氢气、一氧化碳混合气体流经换热器升温后进入电堆。空气由鼓风机带入系统，流经预热单元升温至650°C后进入电堆阴极。电堆内部发生电化学反应产生电能和热能。产生的废气通入燃烧室进行充分燃烧，所产生的烟气通入多级换热器进行余热回收后排出系统。该过程系统结构如图1所示。

考虑到整个发电过程监控变量众多，文中仅选取表征各个组件的七个过程变量对故障传播路径进行分析。传感器分布见图1，所选取变量见表1。

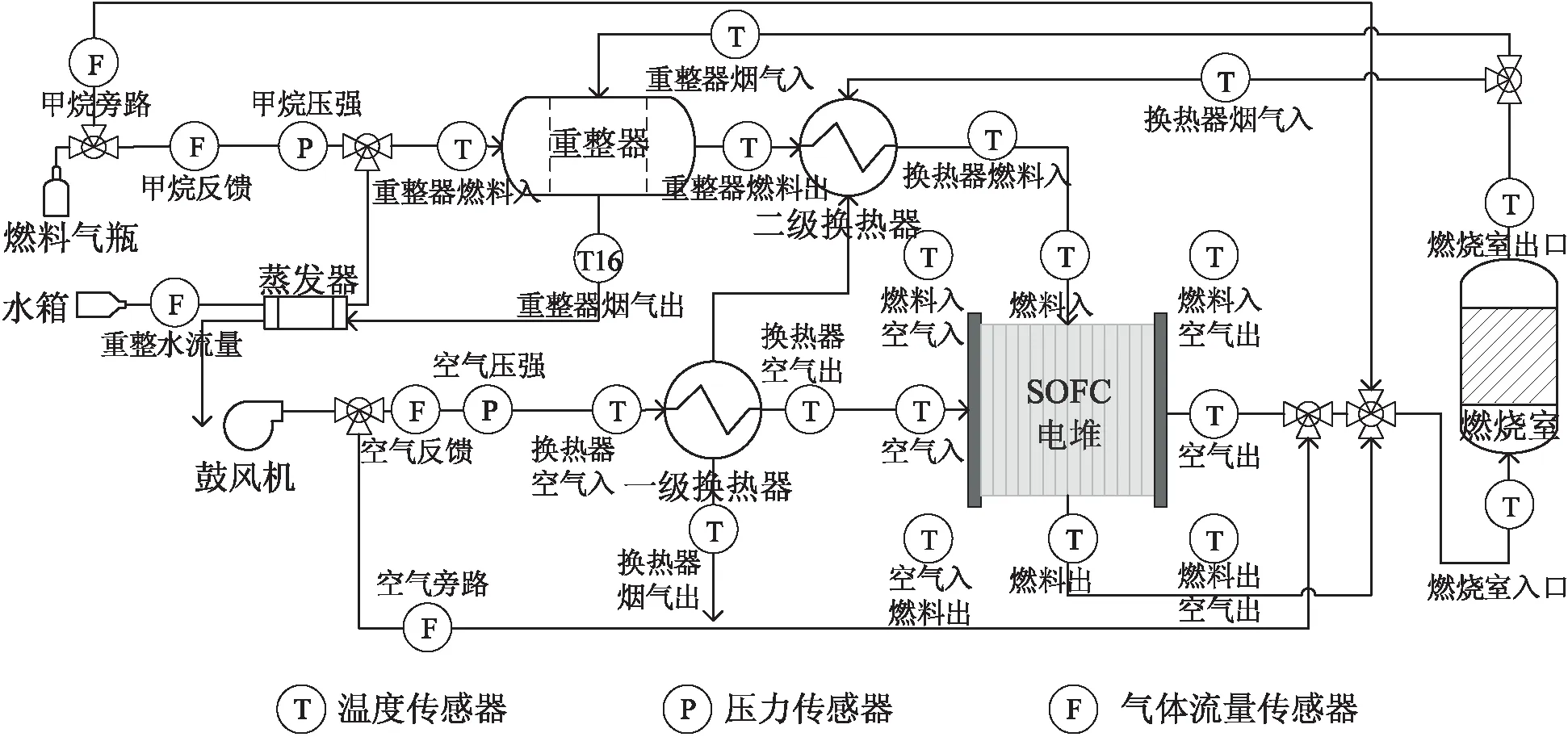
图1 带水蒸气重整SOFC系统流程示意图

限于篇幅，本次实验以该过程中重整水突沸故障数据进行分析。该数据样本表现为系统输出功率波动但未引起性能下降。选取4 600个故障样本进行分析，设4 600×7故障数据矩阵X，为因果分解分析方法输入数据。

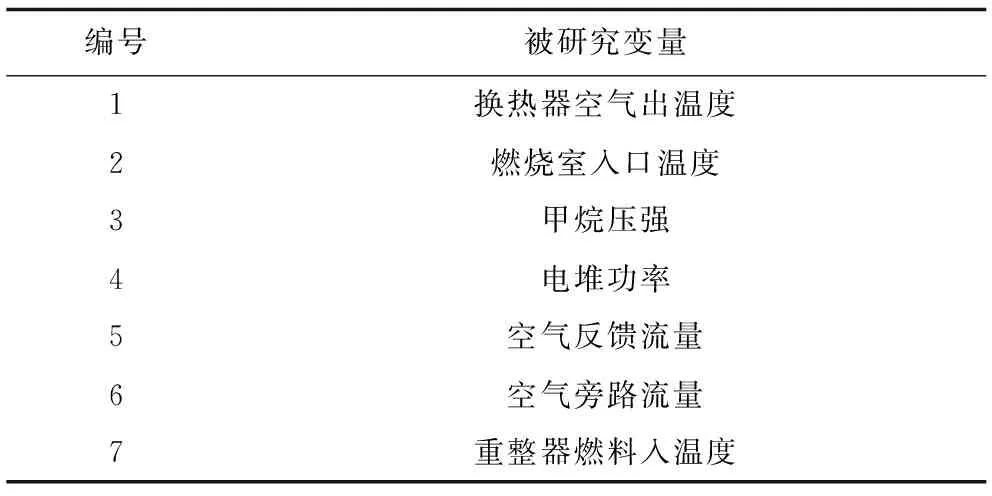
表1 SOFC系统被研究变量

噪声水平β是因果分解中涉及的唯一参数。为避免由于信号分解效果不佳而产生的伪因果检测，在EEMD中确定噪声水平β值的策略是保持IMF正交性的同时最大化成对IMF因果值的可分性。β在[0.05,1]之间按增量为0.05进行取值，两个过程数据分别在β条件下完成EEMD分解，计算非正交泄露指数[15]和成对IMF因果值的均方根。

在文中方法中，选择β的基本准则是保持可接受的非正交泄露指数(<0.05)的同时最小化成对IMF因果值的均方根(理想情况下低于0.05)。依据图2实验结果，选取β值为0.8。

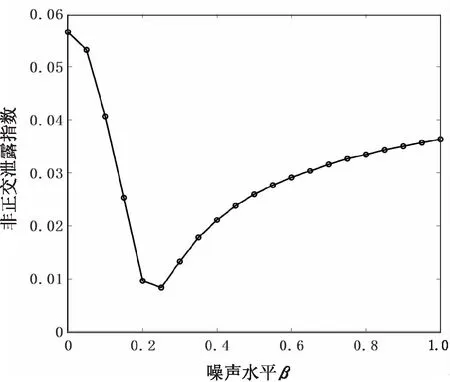
(a)正交性测试

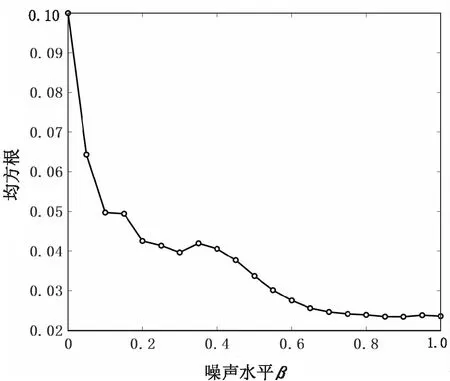
(b)可分性测试图2 EEMD噪声水平β的选取(重整水突沸)

在β=0.8的条件下，对X每一列过程变量时间序列进行EEMD分解，分别产生11个IMF，生成4 600×11×7的矩阵IMFs。依次移除IMF分量，重组再分解，得到4 600×11×7×7的矩阵IMFs'。依据IMFs和IMFs'，估计瞬时相位相关性Coh，Coh'；计算相位相关性偏差，得到7×7×11的因果矩阵D。

表2 IMF分量因果值上限(重整水突沸)

表2给出各IMF分量下因果矩阵的DS1j→S2j上限值，其中IMF1、IMF8～IMF10存在显著的因果关系，指示着故障传播方向。

以IMF1为例，给出详细的因果分析过程，见图3。通过对因果矩阵中显著因果关系的分析，得到了因果路径图，再结合系统各组件的连通性规则，进一步分析故障传播路径。

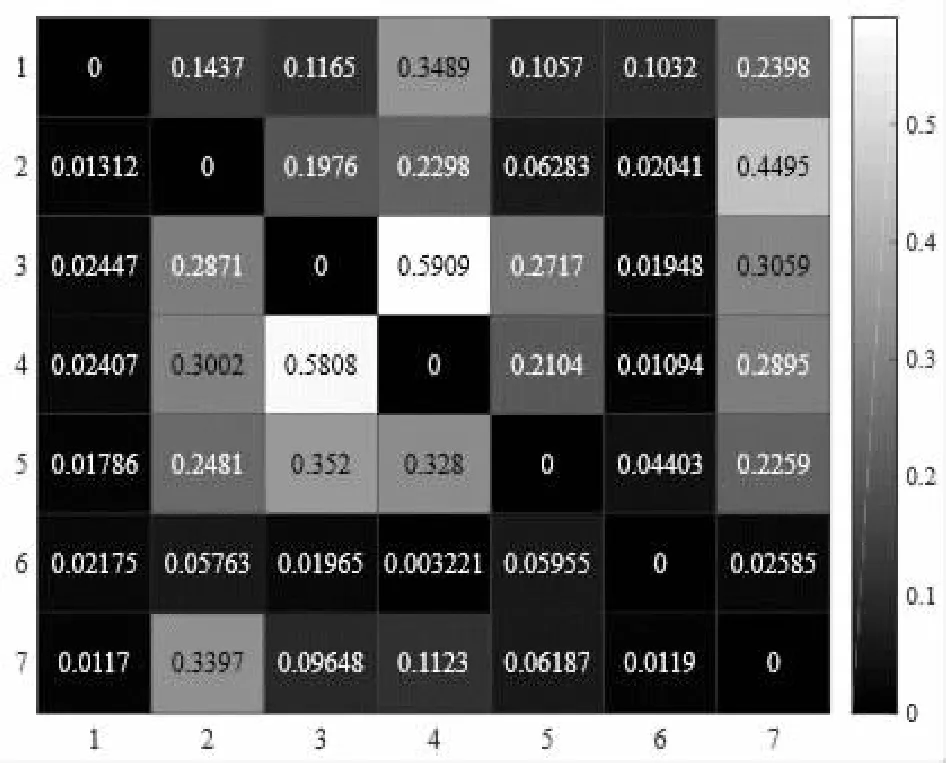
(a)因果矩阵

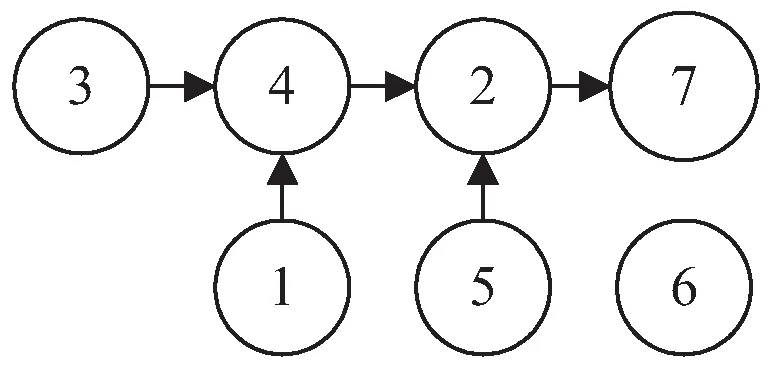
(b)因果路径图

(c)故障传播路径图3 重整水突沸之IMF1分量因果分析

从图3(a)所示，IMF1因果矩阵看出，存在两个显著果变量：电堆功率(1，2，3，5→4)和重整器燃料入温度(2，3，4，1，5→7)。其中，甲烷压强→电堆功率(3→4)和燃烧室入口温度→重整燃料入温度(2→7)两组因果关系尤为突出。因果路径图见图3(b)。结合图1所示传感器分布情况，绘制IMF1分量下的扰动传播路径，见图3(c)。

图4给出IMF8～IMF10因果矩阵，分析如下：

IMF8存在一组显著因果关系，即换热器空气出温度作为果变量，受影响程度更广(→1)。其中，燃烧室入口温度→换热器空气出温度(2→1)尤为突出。结合系统工作原理可知，这是由于燃烧室排烟热回收至换热器引起的，燃烧热的循环再利用使得换热器受到其他组件不同程度的影响。

(a)IMF8分量

(b)IMF9分量

(c)IMF10分量图4 重整水突沸之IMF8～IMF10因果矩阵

IMF9存在一组明显因果作用：甲烷压强→换热器空气出温度→重整燃料入温度(3→1→7)，因果分析同IMF8，其中甲烷压强作为扰动源，而重整器燃料入温度为扰动传播终点。

IMF10因果分析同IMF9。相较于其他IMF分量，甲烷压强→换热器空气出温度(3→1)在IMF10对应时间尺度上尤为显著。

可知，故障传播路径为甲烷压强→电堆功率→燃烧室入口温度→换热器空气出温度→重整器燃料入温度。振荡源为甲烷压力不稳定。因重整反应水蒸气和甲烷供给管道相通，水蒸气的波动影响到腔室内压力波动，表现为通入甲烷压强不稳。由此以推测该故障与重整水突沸有关。

值得注意的是，空气旁路流量不参与上述振荡传播。在空气主干道上增设的冷空气旁路，其目的是通入过量的冷空气，有效控制电堆入口空气温度，从而保证电堆处于热安全状态。相比于过量的空气反馈供给，燃料供给才是引起电堆放电异常波动的关键。

3 结束语

考虑到SOFC系统实际发电过程存在时变、非线性和非平稳性行为，提出了一种基于因果分解的故障根源诊断方法。对输入的观测数据集，进行EEMD分解成不同时间尺度下的平稳振荡信号，信号的重组再分解用于估计瞬时相位相关性偏差，建立各IMF分量下的因果矩阵。该方法通过分析因果瞬时关系以增强双向因果关系检测与分析能力。经SOFC平台真实故障数据验证，该方法能够识别故障传播路径并准确定位故障源，具有较好实用性。