基于通用数控车床的TP蜗杆精密车削方法研究*
2021-10-27田千虎
田千虎,丁 爽
(1.淮安开放大学 机电工程系,江苏 淮安 223005;2.扬州大学 机械工程学院,江苏 扬州 225127)
0 引 言
平面二次包络环面蜗杆副具有多齿同时啮合、承载能力大、传动效率高、齿面接触应力小等优点,被广泛应用于冶金、矿山、太阳能、工业机器人等领域的传动机构中,但其存在参数设计难、精度控制难和制造成本高的问题[1]1001。
在平面包络环面蜗杆副的精确设计建模方面,黄安贻等人[2]基于AutoCAD2000虚拟加工技术,建立了平面包络环面蜗杆的三维实体模型。YANG Jie等人[3]研究了一种建立TP蜗杆齿廓螺旋线的新方法,并对主要设计参数进行了优化选择,以获得更好的啮合性能。YU等人[4]分析了TP蜗杆不同成形参数引起的偏差曲线,调整了5个参数误差,能够提高其加工精度和啮合的性能。侯伯杰等人[5]推导了平面包络环面蜗杆的齿面方程,基于MATLAB建立了环面蜗杆的数字化模型,并基于Solidworks二次开发实现了对环面蜗杆的实体建模。张彦钦等人[6]研究了信息点呈不等距分布的复杂曲面构造方法,基于Unigraphics-Grip编程开发平台,开发了平面包络环面蜗杆传动实体建模系统。刘志等人[7]提出了平面二次包络环面蜗杆副的三维实体模型数字构建方法,通过理论计算啮合点云,采用三维造型软件的曲线曲面拟合,构建了蜗杆副齿面的实体模型。
蜗杆副的建模方法主要分为两种:(1)根据啮合原理,采用数学软件求解齿面方程获得点云数据,再拟合成齿面;可以通过三维造型软件拟合,但存在偏差,且响应慢,也可以采用数学方法直接拟合;(2)直接数字化建模,即利用三维软件的布尔运算生成实体,模型的精度取决于布尔切削步长。
精确建模是制造平面包络环面蜗杆的基础,谭昕等人[8,9]基于NURBS建立了平面二次包络环面蜗杆副蜗轮数字化模型,并采用粗车、磨削的加工工艺加工蜗杆,三轴联动铣削平面二包蜗轮。
平面包络环面蜗杆的加工方式可以分为3类,即车削、磨削和铣削。传统加工方法需要设计带有回转工作台的专用机床,并在回转台上安装切刀盘、铣刀盘和磨头,分别实现车削、磨削和铣削。
针对平面包络环面蜗杆的高效、精密制造难题,学者们提出了通用数控车削技术、虚拟回转中心技术、五轴联动加工技术。基于普通数控车床的新型车削技术[10,11],采用普通切槽刀,利用宏程序和螺纹切削功能,实现了变导程环面蜗杆的快速开齿,可以显著提高加工效率,降低制造成本;但其加工出的齿面为近似齿面,精度低,为直廓环面蜗杆,需进一步磨削才能成型,并且存在磨削余量不均匀的现象[1]1005。邬宗鹏等人[12]提出了一种近似方法,通过分析螺旋线上各点点位规律,确定加工时蜗杆齿面上任意一点的坐标,利用宏程序编制出了环面蜗杆的普通车床加工程序。夏铭等人[13]将余弦定理融入宏程序编程中,采用通用数控车床成功完成了平面包络环面蜗杆的车削加工,提高了加工效率;但其加工精度较低。
针对空间异形曲面的通用精确车削,CHEN Yong-hong等人[14]提出了一种精确车削TI蜗杆的方法,用锥螺旋线拟合两个相邻的离散点。ZHANG Yong等人[15]提出了一种改进的非圆车削方法用于制造底板曲面。李利敏等人[16]针对零件重心和回转重心不重合的异形凸轮,设计了专用夹具,采用数控硬车削方式[17]代替了硬铣削,提高了加工效率,延长了刀具寿命,同时降低了成本。同样地,周海蔚等人[18]设计了一套简单的夹具,用以实现不同偏心距离凸轮的数控车削加工。李铁钢等人[19]基于数控车铣复合加工机床,提出了一种振荡车削的方式来加工异形凸轮类零件,但是其设备的成本较高。
关于带回转工作台的专用机床加工,时礼平等人[20]通过改造普通车床、增加圆工作台带动刀架旋转的方式,实现了对平面二次包络环面蜗杆副的数控加工。韩兴国等人[21]根据平面二次包络环面蜗杆数控磨床的加工原理,基于虚拟回转中心,运用MATLAB数字仿真计算出了蜗杆齿面。
虚拟回转中心技术[22,23]解决了传统加工方法的中心距调节问题,加工工艺范围扩大,安装调整方便,但仍需带有数控回转台的专用机床才可实现数控车、磨和铣削加工,成本较高,可实现工件的批量精加工。五轴联动加工技术[24]需要五轴联动数控机床,成本更高,并且效率低,只适用于工件的单件精加工。
综上所述,现有的通用数控车削技术效率高、精度低,只适用于粗加工;带数控回转工作台的专用机床成本高;五轴联动加工技术成本更高,并且效率低下。
为此,基于普通数控车床的平面包络环面蜗杆高效精密加工方法,本文采用数学方法,完成从齿面方程求解、接触线截取拟合到NURBS齿面拟合重构;基于高精度数字化齿面规划车削螺旋线,计算车削刀位数据,采用锥螺纹车削指令编写TP蜗杆的数控车削程序,并通过仿真切削实验验证该方法的可行性。
1 蜗杆齿面方程
TP蜗杆啮合理论研究有很多成果,本文以右旋单侧齿面为例推导TP蜗杆齿面的成型。
平面包络环面蜗杆齿面是以平面为母面,按照啮合过程展成包络成形。
此处建立的啮合运动坐标系如图1所示。

图1 平面包络环面蜗杆坐标系统β—母平面倾角;φ1,φ2—指某一时刻蜗杆和母平面或蜗轮的转角;a—中心距;rb—蜗轮基圆半径
设S10(O10-x10y10z10)为蜗杆固定坐标系,坐标轴对应的单位矢量定义为(i10,j10,k10);S1(O1-x1y1z1)为与蜗杆齿面固连的动坐标系,坐标轴对应的单位矢量定义为(i1,j1,k1);S20(O20-x20y20z20)为相啮合的蜗轮固定坐标系,坐标轴对应的单位矢量定义为(i20,j20,k20);S2(O2-x2y2z2)为蜗轮动坐标系,坐标轴对应的单位矢量定义为(i2,j2,k2)。
为了表达工具母平面方程,此处建立母平面坐标系Sp(Op-xpypzp),坐标轴对应的单位矢量定义为(ip,jp,kp),xp与x2平行且同向,图1为初始状态与静坐标系x20平行且同向,zp为母线方向。
根据相对运动理论可计算出啮合点处的相对速度为:
v21=ω2×r2-ω1×r1
(1)
ω2=ω2k2
(2)
式中:ω2—母平面或者蜗轮的转动角速度;ω1—蜗杆转动的角速度;r1—蜗杆上啮合点在坐标系S1中的位置矢量;r2—母平面或蜗轮上啮合点在坐标系S2中的位置矢量。
其中,蜗杆转动的角速度ω1为:
ω1=ω1k1=-ω1j20=-ω1(sin(φ2)i2+cos(φ2)j2)
(3)
母平面或蜗轮上啮合点在坐标系S2中的位置矢量r2为:
r2=x2i2+y2j2+z2k2
(4)
式中:x2—蜗轮啮合点的x坐标;y2—蜗轮啮合点的y坐标;z2—蜗轮啮合点的z坐标。
蜗杆上啮合点在坐标系S1中的位置矢量r1为:
r1=x1i1+y1j1+z1k1
(5)
式中:x1—蜗杆啮合点的x坐标;y1—蜗杆啮合点的y坐标;z1—蜗杆啮合点的z坐标。
为了简化计算,此处令ω2=1,则有:
ω1=i12
(6)
式中:i12—传动比。
经整理并计算可得:
(7)
母平面的法矢在坐标系S2中的方程为:
(8)
两齿面的正确啮合条件是两齿面在啮合点位置的公法线垂直于它们在该点的相对速度,即:
Φ=n·v21=0
(9)
将式(7,8)代入式(9),可以得到一次包络的啮合方程,即:
(10)
令母平面上任意一点在Sp中的坐标为(u,0,v),则根据坐标变换矩阵,可得到母平面上的点在坐标系S2中的表达式:
(11)
在母平面上,满足式(10)啮合方程的点云变换到坐标系S1中,即构成了平面包络环面蜗杆齿面,即:
(12)
联立式(10~12),即可计算出平面包络环面蜗杆的点云数据。另一侧齿面的方程可参见文献[25]。
2 数字齿面重构
蜗杆齿面受齿顶圆环面和齿根圆环面的约束,此处建立母平面上啮合点坐标u的边界区间为:
(13)
式中:Ra1—蜗杆顶圆半径;Rf1—蜗杆根圆半径;rb—蜗轮基圆半径。
同时,受蜗杆齿面轴向长度L的限制,建立蜗杆轴向的边界区间,即:
(14)
蜗轮蜗杆传动过程中,在某一转角下,可计算出满足式(10)啮合方程的一系列空间点坐标,这些点构成了一条接触线。
改变蜗轮或蜗杆的转角,可计算出系列不同的接触线,蜗杆数字化齿面即由系列接触线组成。
蜗杆齿面重构具体步骤如下:
(1)根据蜗杆副的基本设计参数,确定蜗杆齿高参数u和蜗轮包络转角φ2的取值区间;
(2)将u在取值区间上等值地离散为m个点,φ2在取值区间上等值地离散为n个点;
(3)确定一转角φ2,取m个u值,分别根据式(10)计算出v值,即可得到母平面上满足啮合方程的m个空间啮合点参数(u,v),代入式(11,12)即可求得m个啮合点在蜗杆坐标系S1中的坐标,这m个S1坐标系中的啮合点构成了蜗杆齿面上的一条接触线;
(4)令φ2取不同的值,重复步骤(3)即可求出蜗杆齿面上所有接触线,如图2所示;

图2 蜗杆齿面接触线
(5)计算出接触线后,根据蜗杆齿面边界约束条件剔除范围外的接触点,剔除过程中按二分法确定接触线与边界约束的交点及其参数;
(6)由于每条接触线上剔除的点数不一致,难以构成均匀的网格点阵列。笔者采用NURBS曲线拟合方法对每条接触线进行拟合,再将每条接触线等值地离散为m个点;
(7)根据均匀的网格点阵列,笔者采用NURBS曲面拟合的方式拟合重构蜗杆数字齿面,对蜗杆齿面进行可控均匀离散。
重构后的蜗杆齿面如图3所示。

图3 重构后的蜗杆齿面
接触线求解过程中,离散点数的疏密决定了重构的数字化曲面精确程度。
3 车削刀位计算及编程
笔者根据重构的蜗杆齿面可计算出均匀的网格点坐标及其法矢量,沿齿向方向提取空间螺旋线,如图4所示。
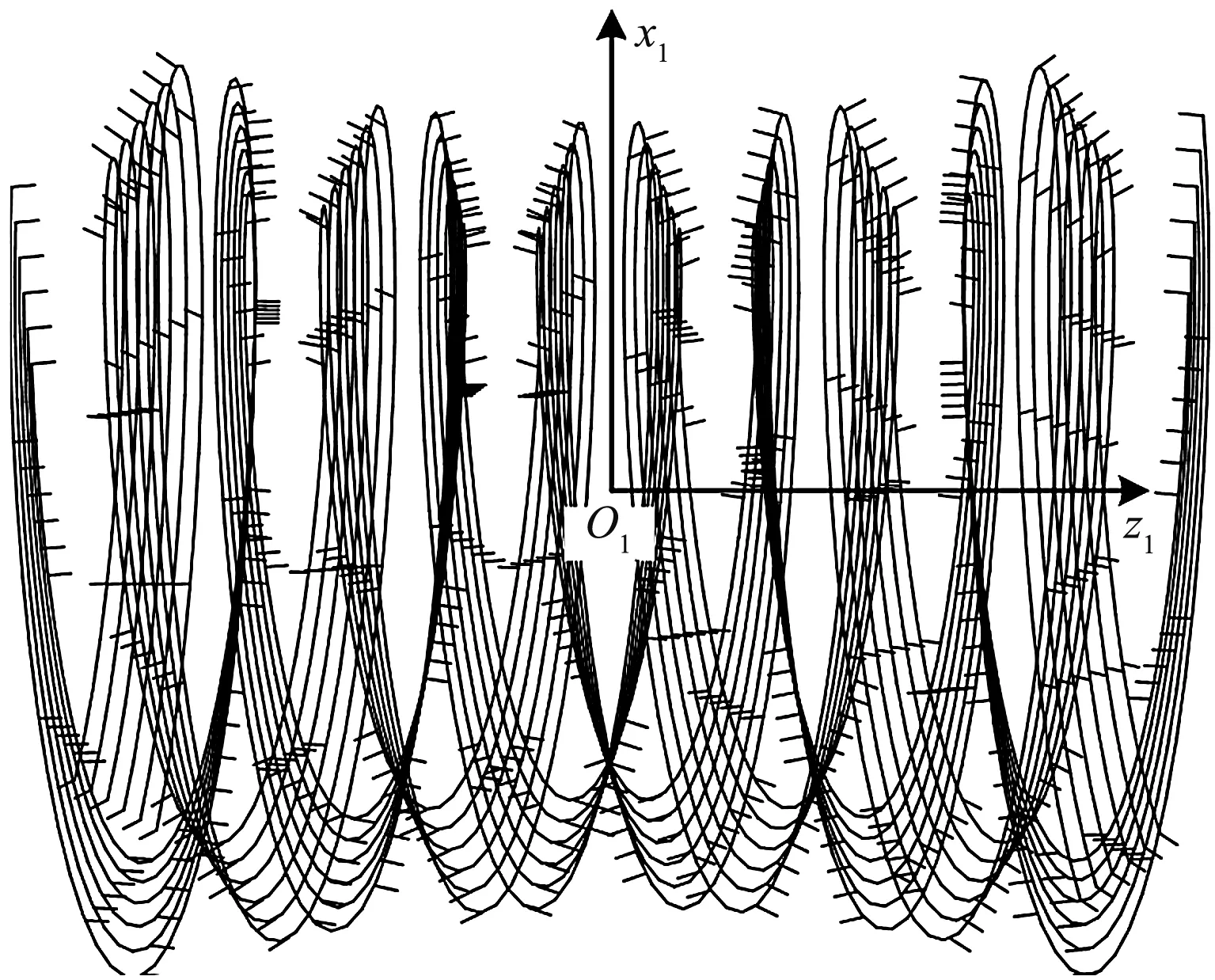
图4 车削轨迹线及法矢量
此处设螺旋轨迹线上任一点的坐标为ph(pxh,pyh,pzh),齿面单位法矢量为nh(nxh,nyh,nzh)。
首先,将蜗杆齿面上的点转换为极坐标形式:
(15)
然后,根据式(15)将ph(pxh,pyh,pzh)转换为极坐标形式(prh,pzh,θph);将齿面单位法矢量旋转变换到XZ平面,得到XZ平面中的齿廓单位法矢量,即:
(16)
式中:矢量(nxh1,nzh1)—XZ平面中的齿廓单位法矢量。
最后,可计算出直接用于编程的车削刀位如下:
(17)
将同一环面螺旋线上的相邻两刀位点极坐标表达为(Cprh(i+1),Cpzh(i+1),θph(i+1))和(Cprh(i),Cpzh(i),θph(i)),i+1和i分别指同一环面螺旋线上的第i+1和第i个刀位点。
数控车削代码可编写为:
G32X2×Cprh(i+1)ZCpzh(i+1)Fmax(Cprh(i+1)-Cprh(i),Cpzh(i+1)-Cpzh(i))/(θph(i+1)-θph(i))×2π。
其中:X,Z—车床X轴和Z轴的指令字地址;F—螺距地址。
4 仿真切削实验
此处笔者以某型号的TP蜗杆为例,采用仿真切削软件来验证所提方法的可行性及正确性。
笔者采用的通用数控车床为卧式平床身结构,刀架后置;同时,为了简化建模过程,笔者仅建立了组件坐标系统,用以控制X轴、Z轴平动,以及主轴的转动;
采用刀头宽度为2 mm,刀尖圆弧半径为0.4 mm的普通切槽刀,根据加工的蜗杆旋向、刀架位置,确定主轴正转、刀具反装。
笔者建立的仿真切削环境如图5所示。
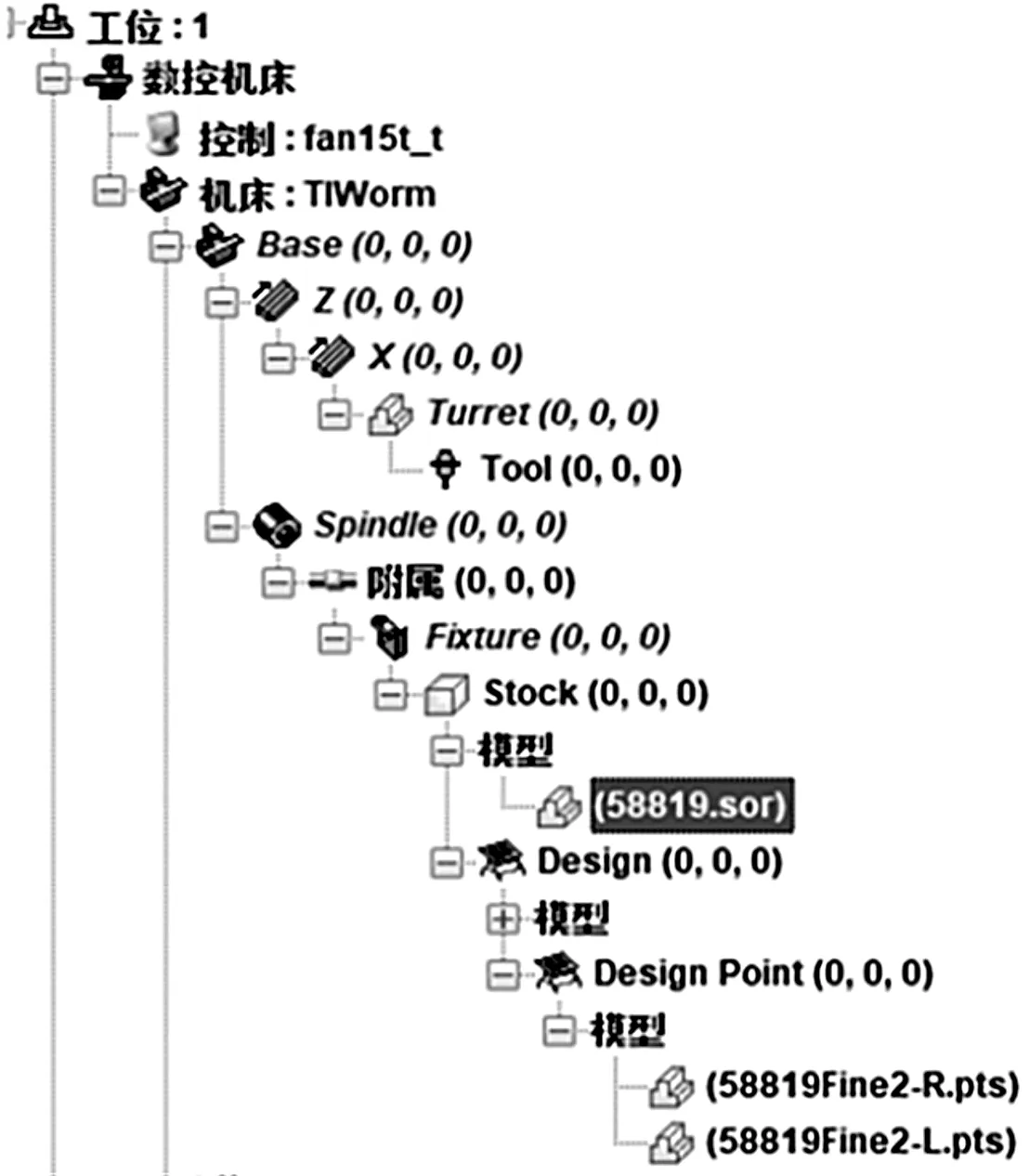
(a)仿真车床组件系统

(b)仿真刀具及工件示意图
笔者将理论啮合计算的TP蜗杆空间点坐标及法矢量导入到仿真切削软件中,作为精度分析测量设计点;计算精加工环面螺旋轨迹刀位时,分别取环面蜗杆的网格点行数(齿廓方向)和列数(齿向方向)为300行300列和50行100列两种设计值;检测点数均取为10行50列,去除检查距离之外的点。
仿真切削及精度分析结果如图6所示。

(a)仿真切削结果及检测点位
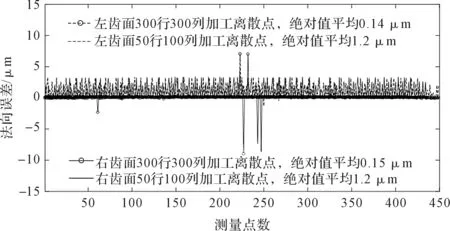
(b)法向误差
结果图6中的结果表明:
采用本文方法加工的TP蜗杆,其齿面误差均匀、精度高,50行100列加工误差绝对值平均为1.2 μm;网格点加密后,齿面加工精度显著提升,但由于程序段增加,加工效率会有所下降;采用50行100列的数控车削NC代码为5 000行,主轴转速为400 r/min时,粗精加工单个蜗杆的时间可控制在5 min内,在保证精度的同时,加工效率可以得到显著提高,因此该加工方法适用于蜗杆的批量生产。
此外,采用通用数控车床的加工成本更低,因此本文方法有很好的推广应用价值。
5 结束语
由于平面包络环面(TP)蜗杆空间螺旋齿面的制造存在问题,笔者提出了一种在通用数控车床上用标准切槽刀精确车削TP蜗杆的方法;首先根据平面包络环面蜗杆啮合原理推导了TP蜗杆的齿面方程,然后基于NURBS建模方法建立了蜗杆齿面的数字化模型,研究了环面蜗杆的通用数控车削方法;最后通过仿真切削试验验证了该方法的可行性。
研究结果表明:
(1)控制齿面网格点疏密,直接影响到齿面车削的精度和效率;当数控车削代码5 000行,主轴转速为400 r/min时,粗精加工单个蜗杆的时间可控制在5 min内,齿面误差控制在1.2 μm,在保证精度的同时,加工效率得到显著提高,适用于批量生产;
(2)与传统方法相比,在保证齿面精度的前提下采用该方法可显著提高加工效率,且采用通用数控车床的成本较低,为批量、高效、高精、低成本的TP蜗杆制造提供了可能。
在后续的研究当中,笔者将把该方法推广到其他廓形的空间异形螺旋曲面通用数控车削中,并开发零编程CAM软件;同时,研究数控车床的实际制造误差,探索环面蜗杆制造精度的提升策略,优化其啮合的性能。
