基于1.5维谱活跃频率的行星齿轮箱磨损故障诊断研究*

毕浩程,蒋章雷,李宇恒,吴国新,王红军

(北京信息科技大学 现代测控技术教育部重点实验室,北京 100192)

0 引 言

齿轮箱作为旋转机械的核心部件,广泛地应用于减速比大、功质比大的机械传动系统中[1]。齿轮箱的加工工艺复杂、装配精度要求高。

在齿轮箱实际工况中,由于环境恶劣等因素,使得其易受到损伤,从而导致整个机械设备发生故障,造成经济损失和人员伤亡[2,3]。因此,对齿轮箱磨损故障进行诊断具有重要意义。

作为传动系统,齿轮箱包含有齿轮、轴承、轴、箱体等部件。在齿轮箱的所有故障中,因齿轮引发的故障占其比重达60%;而其中,齿轮的点蚀和磨损又占到齿轮失效的41%[4,5]。

由于行星齿轮箱内部结构复杂,工作环境复杂多变,导致其振动信号中包含有大量的噪声。针对这些问题,国内外许多学者进行了大量的研究。雷亚国等人[6]建立了行星齿轮箱振动信号仿真模型,通过实验对比分析,总结出了行星齿轮箱不同齿轮局部故障的振动信号特点。SUN R等人[7]建立了行星齿轮箱动力学仿真模型,提出了一种加权稀疏表示方法来提取其特征,成功地诊断出了行星齿轮箱的故障。金棋等人[8]提出了一种基于深度学习的多样性特征提取方法,并将其信息进行融合,有效地提高了行星齿轮箱的故障诊断精度与稳定性。刘清清等人[9]将双树复小波引入振动到齿轮箱信号分析中,有效地抑制了其中虚假频率的出现,并准确提取出了其故障特征,准确地诊断出了多种类型的齿轮箱故障。WANG D等人[10]提出了一种新的提取瞬态周期性脉冲成分方法,利用动态贝叶斯推理对先验小波参数分布进行了迭代后更新,成功地识别出了机械故障中的瞬态周期性脉冲成分。

总结上述研究现状可知,目前对于齿轮箱的研究工作主要集中在其特征提取、故障诊断方面。

近年来,已有很多方法被用于提取行星齿轮箱的故障特征,例如:短时傅里叶变换、小波变换、经验模态分解(EMD)、变分模态分解(VMD)等。这些方法均有各自的不足和局限性:(1)短时傅里叶变换不能同时获得较高的时频分辨率[11];(2)小波变换高频频率分辨能力弱,且会丢失相位信息[12];(3)经验模态分解缺乏严格的数学理论基础,存在过包络、欠包络、模态混叠和端点效应等问题[13];(4)变分模态分解结果受惩罚因子和模态分量个数的影响较大[14]。

目前,一阶统计量和二阶统计量已被广泛应用于机械振动信号的分析中[15],但这些方法只适用于分析线性和高斯信号。

在实际工程中,由于振动信号复杂,需要从更高阶次去反映其信号特征[16]。高阶统计量是指阶数大于二阶的统计量,包括高阶矩、高阶累积量、高阶矩谱,等。高阶累积量是解决非线性、非平稳、非高斯、非最小相位、非因果信号的主要手段[17]。MENDEL J M[18]提出了利用高阶累积量的一维片段及其一维傅里叶变换,作为从高阶累积量中提取有用信息的方法,即对高阶累积量做切片处理,主要包括1.5维谱(三阶累积量对角切片谱)方法。

1.5维谱能有效抑制高斯噪声,识别信号的二次相位耦合[19]。在已有的相关文献中,是将二次相位耦合推广到符合实际意义的二次频率耦合,并解耦出参与耦合的频率和耦合产生的频率。但是行星齿轮箱实际工况复杂,齿轮箱中各种频率相互耦合,通过图像无法直接提取出其信号的故障特征。

本文通过将1.5维谱解耦出的参与耦合的频率与耦合产生的频率逐点相乘,得到其活跃频率,直接提取信号故障特征,为行星齿轮箱的磨损故障诊断提供理论基础。

1 1.5维谱活跃频率指标的基本原理

1.1 1.5维谱的定义

一个非高斯平稳随机过程x(n)的三阶累积量为:

c3x(τ1,τ2)=cum(x(n),x(n+τ1),x(n+τ2))

(1)

式中:τ1,τ2—时延;cum—统计均值。

定义三阶累积量的一维对角切片为[20]:

(2)

定义三阶累积量一维对角切片的一维傅里叶变换为:

(3)

公式(2)称为三阶累积量一维对角切片谱,或称为1.5维谱。

由于1.5维谱方法仅使用了三阶累积量的对角线切片,而且只进行了一维傅立叶变换,可以大大减小计算量。

1.2 1.5维谱活跃频率的获取

设振动信号为:

(4)

式中:ai—幅值常数;ωi—角频率;φi—[0,2π)上均匀分布的独立随机变量。

其共轭为:

(5)

x(t)的傅氏变换为:

(6)

式中:δ—脉冲函数。

根据各项取共轭与否,复数谐波信号的三阶累积量具有8种定义。为了分析二次相位耦合,保证当谐波信号中不存在二次相位耦合时,复数谐波信号的三阶累积量为零,分析参与耦合频率分量选用如下形式:

C3x(τ1,τ2)=cum[x*(t),x*(t+τ1),x(t+τ2)

(7)

振动信号x(t)的三阶累积量对角切片谱(1.5维谱)为:

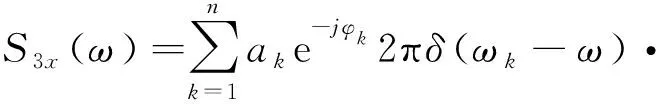
(8)

当ω=ωk时:

(9)

由脉冲函数性质可知,只有当ωk=ωq-ωp时,振动信号x(t)的三阶累积量对角切片谱S3x(ωk)≠0。

分析耦合产生频率分量选用如下形式:

C3x(τ1,τ2)=cum[x*(t),x(t+τ1),x(t+τ2)]

(10)

振动信号x(t)的三阶累积量对角切片谱(1.5维谱)为:

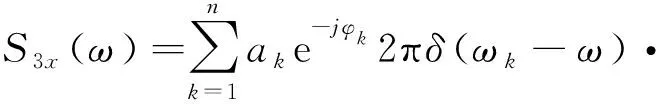
(11)

当ω=ωk时:

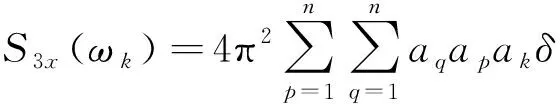
(12)

只有当ωk=ωp+ωq时,振动信号x(t)的三阶累积量对角切片谱S3x(ωk)≠0。

由式(8,11)可知:三阶累积量对角切片谱的幅值在某个频率处不为零,那么这3个频率必须满足二次频率耦合的条件。且公式中傅里叶变换的结果为复数,在绘制信号频谱时需进行相应的取模运算,因此,信号相位不会影响二次频率耦合的幅值大小。

由于行星齿轮箱工作环境恶劣,且其周围的环境又存在着大量的噪声,单纯通过1.5维谱无法直接地提取出行星齿轮箱信号的故障特征。

1.5维谱能解耦频率耦合的部分,将耦合频率解耦成参与耦合频率与耦合产生频率两部分,在参与耦合频率和耦合产生频率中存在重复的频率,把既参与耦合的频率又耦合产生的重复频率看作是活跃的,定义为活跃频率;

笔者将参与耦合频率与耦合产生频率两者逐点相乘,使得重复的频率幅值凸显出来,通过观察活跃频率与故障频率之间的关系,来判断行星齿轮箱是否发生故障。

设1.5维谱参与耦合频率分量为:

(13)

1.5维谱耦合产生频率分量为:

(14)

则1.5维谱活跃频率分量为:

C(ωk)=A(ωk)·B(ωk)

(15)

据此来判断行星齿轮箱是否发生故障。

2 仿真信号分析验证

笔者接下来对仿真信号进行分析验证。

设仿真信号为:

(16)

式中:fi—随机定义的频率;φi—[0,2π)上均匀分布的独立随机变量。

其中:f1=8 Hz,f2=15 Hz,f3=21 Hz,f4=44 Hz,f5=23 Hz,f6=40 Hz,f5=f1+f2,φ5≠φ1+φ2,f4=f3+f5,φ4≠φ3+φ5,f6不参与任何形式的耦合。

笔者绘制了仿真信号1.5维谱图,如图1所示。

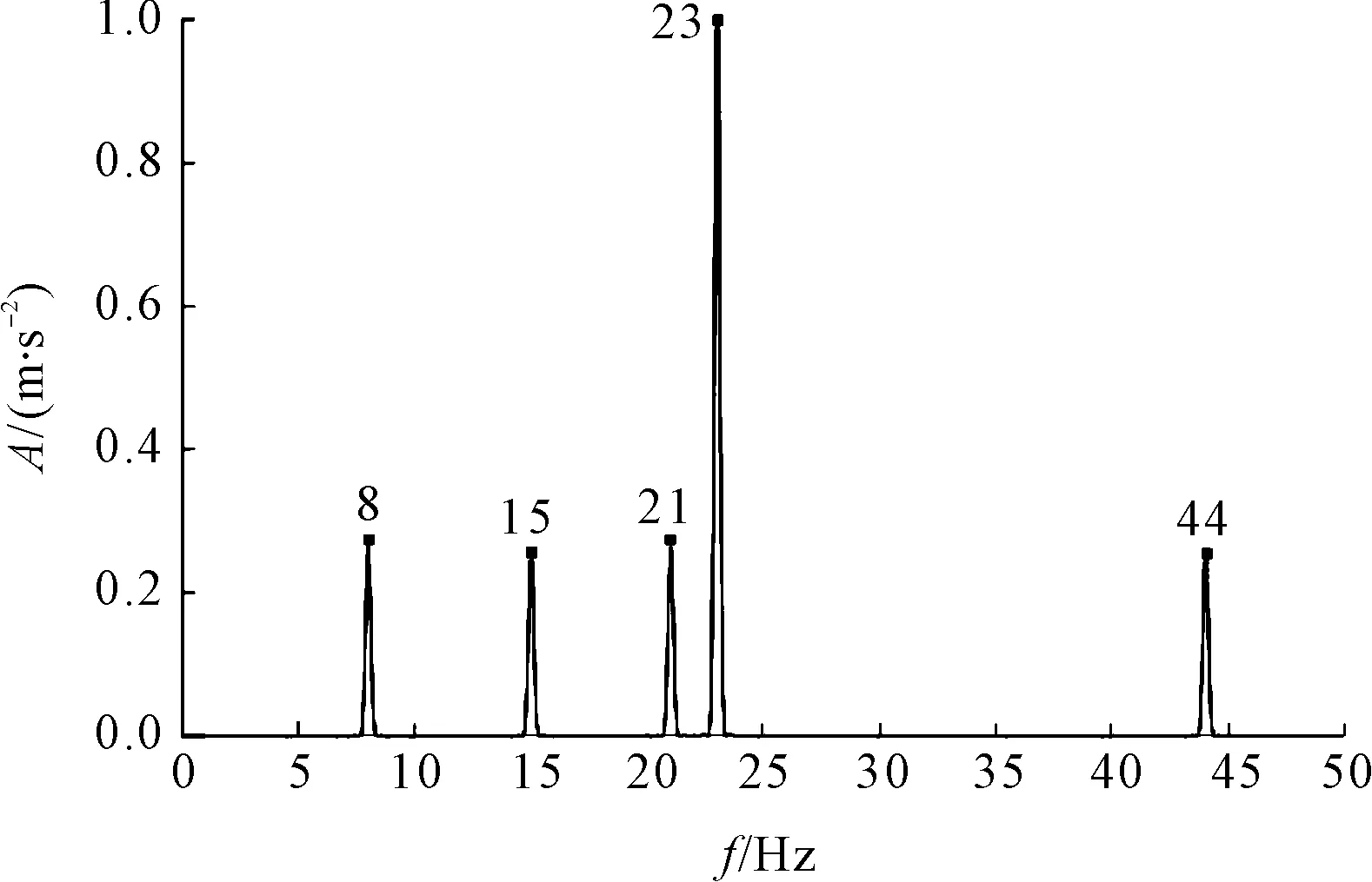
图1 仿真信号1.5维谱图

笔者绘制了仿真信号1.5维谱活跃频率图,如图2所示。

图2 仿真信号1.5维谱活跃频率图

在图1中,只有进行二次频率耦合的8 Hz,15 Hz,21 Hz,23 Hz,44 Hz这5个频率在1.5维谱中显示,不参与任何耦合的40 Hz被抑制。由此可见,1.5维谱可以检测出只满足二次频率耦合的频率成分。

在图2中,f5作为活跃频率显示,因为f5=f1+f2,f4=f3+f5,f5既参与耦合又耦合产生,是重复的频率部分,所以在1.5维谱活跃频率图中被提取出来。

3 实验及结果分析

3.1 行星轮磨损数据获取

为了验证该方法的有效性,笔者搭建了行星齿轮箱磨损故障实验台系统,如图3所示。

图3 行星齿轮箱齿面磨损故障试验台

在图3中可以看到:该系统由行星齿轮箱、电机、制动器及其控制器、数据采集系统(加速度传感器、电涡流传感器等)等组成。

测点1～3布置加速度传感器,测量振动信号:测点1对应行星齿轮箱第二级的位置(与水平方向成45°角);测点2、3分别对应第三级垂直和水平位置;测点4放置电涡流传感器,配合测速齿轮盘可得出输出轴实时转速。

此处笔者设置采样频率为20 480 Hz,采样时间10 s,采样间隔为10 min;设置行星齿轮箱总传动比77.3,高速轴转频为600 r/min;设置磁粉制动器转矩为8.33 N·m。

正常状态下的齿轮和磨损状态行星轮如图4所示。

图4 正常状态和磨损状态行星轮

行星齿轮箱的参数如表1所示。

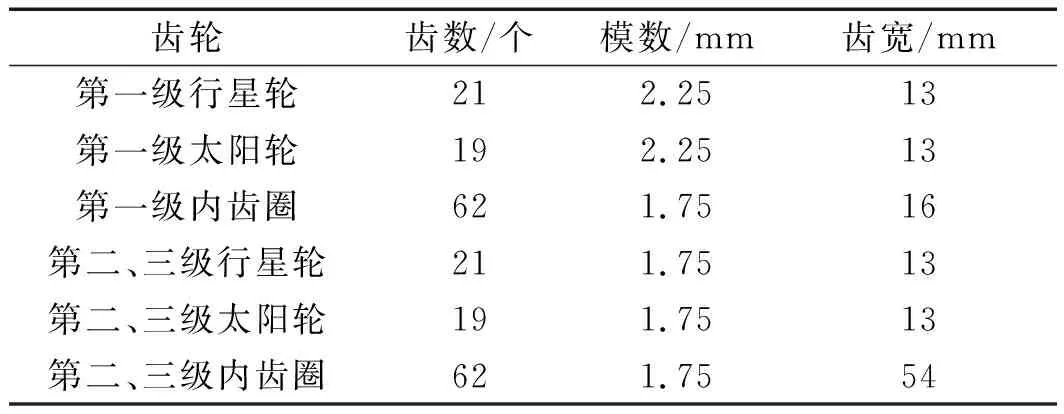
表1 行星齿轮箱的参数

经计算可得到齿轮转频及啮合频率,如表2所示。

表2 齿轮转频及啮合频率

齿轮的故障特征频率如表3所示。

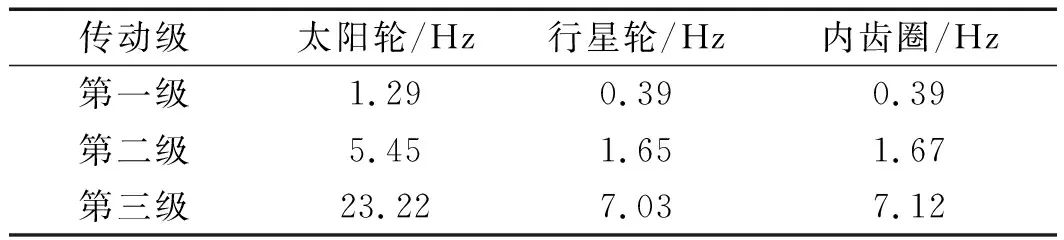
表3 齿轮故障特征频率

3.2 结果分析

在行星齿轮箱磨损故障实验中,笔者将齿面正常的数据绘制成频谱图和1.5维谱活跃频率图,如图5所示。

笔者将具有齿面磨损故障的数据绘制成频谱图和1.5维谱活跃频率图,如图6所示。

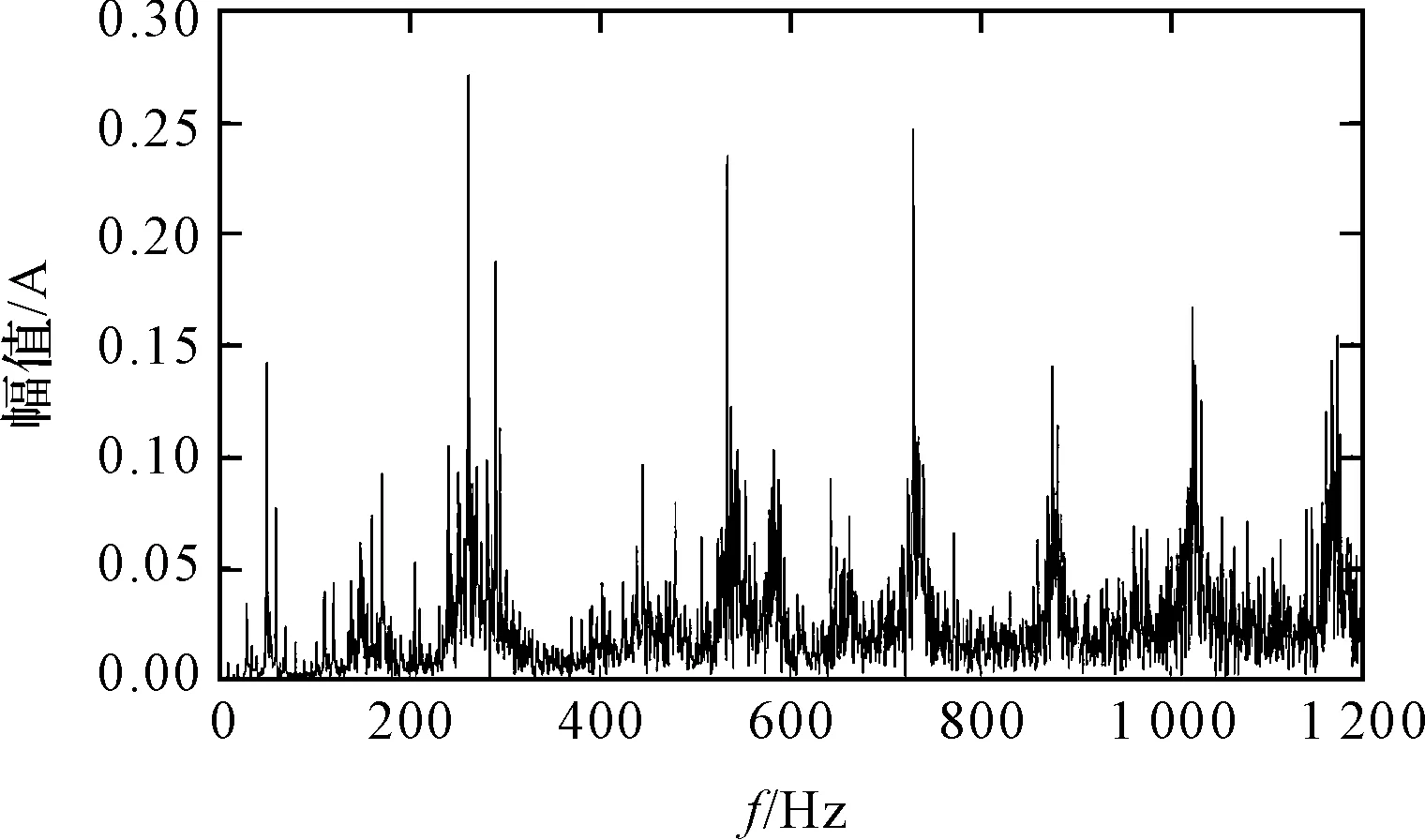
(a)正常数据频谱图

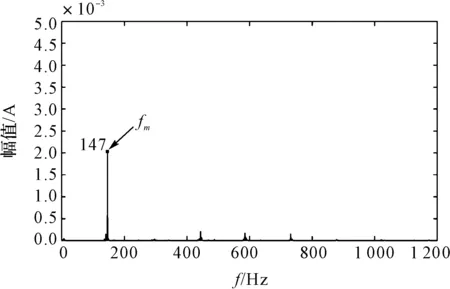
(b)正常数据1.5维谱活跃频率图

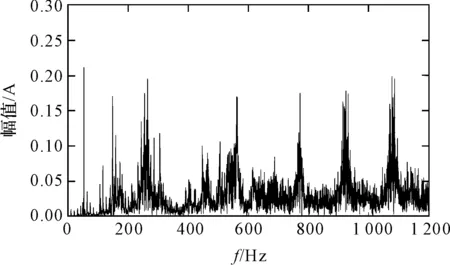
(a)齿面磨损故障数据频谱图

(b)齿面磨损故障数据1.5维谱活跃频率图

从图5(a)和图6(a)中可以看到:正常数据和齿面磨损故障数据的傅里叶变换频谱图中噪声较多,且磨损故障数据的傅里叶变换频谱图比正常数据傅里叶变换频谱图更加复杂,这是由于行星齿轮箱中存在包含故障频率的多种频率成分,其相互调制的结果,导致谱图更加复杂,难以观察到齿轮箱故障特征频率。

从图5(b)中可以看出:对正常数据做1.5维谱活跃频率分析,只有147 Hz幅值最高,其他活跃频率幅值很低;而最活跃频率147 Hz约等于齿轮的啮合频率fm=147.05 Hz,这说明在齿轮箱正常运转的情况下,1.5维谱分析后活跃频率是齿轮的啮合频率。

在图6(b)中,笔者对齿面磨损故障数据做1.5维谱活跃频率分析,最活跃频率154 Hz=fm+fp=147.05 Hz+7.03 Hz=154.08 Hz。其中:fp—第三级行星轮故障频率,最活跃频率等于齿轮啮合频率与故障频率耦合产生的频率。

以上结果说明:在齿轮箱发生磨损故障时,行星轮磨损故障频率fp出现次数增多,1.5维谱分析后活跃频率是啮合频率与故障频率耦合得到的频率,所以可以用1.5维谱活跃频率,作为判断行星轮是否发生磨损故障的依据。

4 结束语

本文通过将1.5维谱解耦出的参与耦合的频率与耦合产生的频率逐点相乘,得到其活跃频率,直接提取信号故障特征,从活跃频率中是否包含磨损故障频率来判断行星齿轮箱是否发生磨损故障,为行星齿轮箱的磨损故障诊断提供了理论基础;笔者搭建了行星齿轮箱磨损故障实验台系统,对该方法进行了验证。

实验及研究结果表明:

(1)1.5维谱能够识别二次频率耦合,能够将参与耦合频率与耦合产生频率解耦出来;

(2)1.5维谱活跃频率能够代表频率耦合中最活跃的部分;

(3)与传统傅里叶变换方法相比,1.5维谱活跃频率能够更加快速、直观地实现对行星齿轮箱齿面磨损故障的诊断。

由于1.5维谱只能识别二次频率耦合,而在实际行星齿轮箱的振动信号中可能存在更多频率的耦合方式,这将是笔者今后研究的一个方向。