波浪作用下涵洞式直立堤水体交换特性研究

吕超凡，赵西增,2，殷铭简

(1. 浙江大学 海洋学院，浙江 舟山 316021; 2. 浙江海洋大学 海洋工程装备学院，浙江 舟山 316022)

重力式防波堤虽然能较好地起到挡浪作用，但它在一定程度上阻止港池内外水体之间的自然循环和交换[1-2]，使得港内水质恶化，产生一系列的环境问题[3]。为在挡浪的同时，加强港池内外水体交换，可在防波堤的水下部分开挖涵洞，形成涵洞式防波堤。利用波能主要集中在水面附近的特点，防波堤的上部结构可以反射波浪，水下涵洞部分可进行水体交换[4]。该措施既可满足港池的泊稳条件，又可提高港池的水质；相较于其他常见的水体交换方式，具有结构强度高、经济性好、施工容易等优点[2]。

总体而言，针对涵洞式防波堤的消浪及透波特性研究己较为详尽。但在水体交换更新方面，虽然已有基于浅水方程的大尺度数值模拟，但其针对的是潮流，波浪作用下的水体交换机理及其规律尚缺乏相关研究。为此，采用计算流体力学(CFD)数值模拟[11-13]结合物理模型试验[14-15]的方式精细化研究涵洞式直立堤在波浪作用下涵洞内部水体的交换特性。数值模拟基于高精度的VPM (volume-average/point-value method)-THINC (tangent of hyperbola for interface capturing)/QQ (quadratic surface representation and Gaussian quadrature)模型[16-17]，该模型可以精确捕捉自由面，重现波浪与涵洞式直立堤的相互作用，为分析其运动机理提供依据[18]。此外，在其基础上提出一种能够标记涵洞内外水体变化的双液相流体体积(VOF)方法[11]。该方法主要是把原有的计算水体分成多个子水体并分别标记，而后计算其各自输运方程，进而获取不同水体的运动特征，以此来反映在水动力的作用下，水体内部的流动规律。该方法可以同时获取涵洞内部的水体流动以及整个水体的流动，相对简单，计算成本低[19]。由此，文中利用上述方法定性以及定量描述涵洞内外水体的交换特性，而后结合局部流场揭示水体交换机理，并分析不同涵洞参数以及波浪参数对水体交换的影响。

1 数值方法

1.1 基本方程

CFD数值模拟采用不可压缩黏性流模型，其控制方程如下：

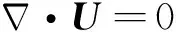
(1)

(2)

(3)

式中：U(x,z)为流体质点速度，ρ为流体密度，p为相对动压力，m为动力黏性系数，U(x,z)为加速度，U(x,z) 为坐标点，Fσ(x,z)为表面张力。Fσ表达式如下：

(4)

式中：σ为张力系数，κ为界面平均曲率，α为流体体积分数。当网格单元为空气时，α=0；为水时，α=1；水汽掺混时，0<α<1。另外每个网格的流体特性定义如下：

λ=λ1α+λ2(1-α)

(5)

式中：λ可为网格内流体的密度ρ或黏性系数μ。

其中，Navier-Stokes方程采用高阶有限体积法VPM求解，自由面采用高精度的THINC/QQ算法[17]重构。建立基于OpenFOAM底层函数库的VPM-THINC/QQ模型，具体可参考文献[18]。

为实现数值波浪水槽的造波与消波，采用速度边界法造波[18]，以及 Jacobsen等[20]提出的松弛法来消除透射波和二次反射波。

1.2 双液相算法

为直观反映涵洞式直立堤的水体交换特性，在VPM-THINC/QQ模型的基础上提出一种能够模拟港池内外水体交换的双液相VOF方法[19]。该方法假设两种性质相同的液体分别为β1和β2，两种液体均满足VOF输运方程：

(6)

(7)

其中，

β1+β2=α

(8)

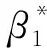
(9)

(10)

由此，港池外部以及涵洞内部水体标记为β1，港池内部水体标记为β2，开展基于双液相VOF方法的涵洞式直立堤水体交换特性研究。

2 试验以及CFD数值模型布置

为定性以及定量分析涵洞式直立堤的水体交换特性，物理模型试验以及数值模拟布置如下。

2.1 试验设备及模型布置

物理模型试验在波浪水槽内进行，水槽尺寸为25 m×0.7 m×0.7 m(长×宽×高)。水槽首端装有主动吸收式推板造波机，可产生单向二维正弦规则波，目标波浪生成质量不受造波时间影响，水槽尾端配有消波设施来消除波浪反射。模型试验布置见图1，试验水槽中设置6根浪高仪，分别为EG1～EG6，所在位置依次为5 m、10 m、11 m、13 m、16 m、17 m，防波堤模型置于14 m处。模型采用亚克力板制作，防波堤长度为B=0.5 m，涵洞高度及深度可调节，试验水深h=0.4 m。具体试验工况如表1所示，其中S为涵洞高度，dS为涵洞中轴线位置，Ti为试验周期，Hi为试验波高。

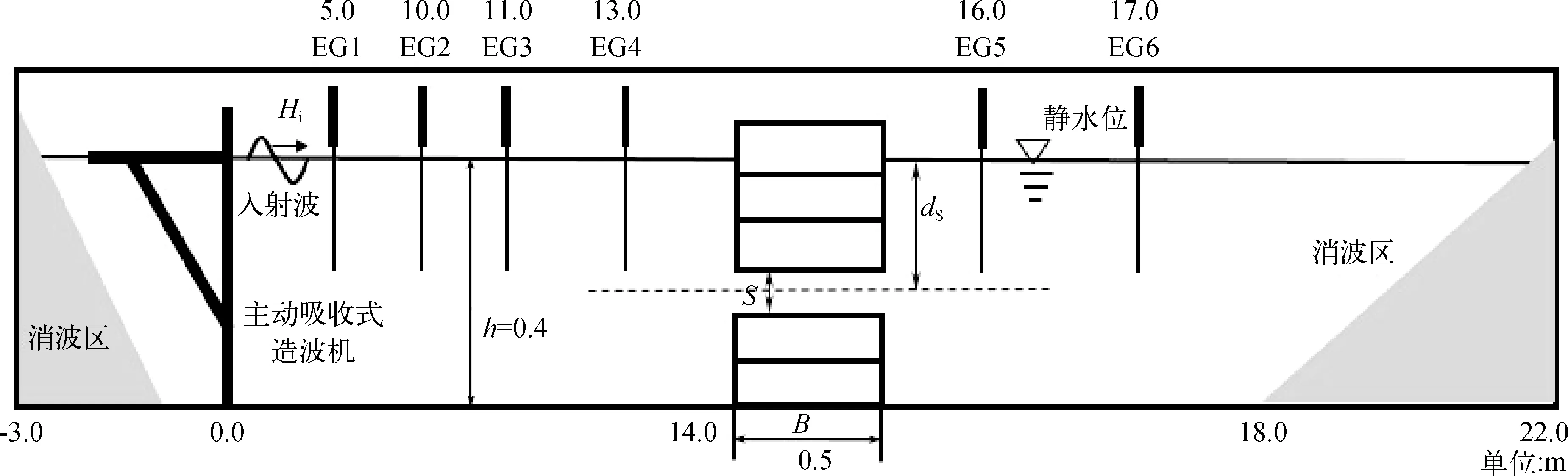
图1 物理模型试验布置Fig. 1 Sketch of an experimental setup

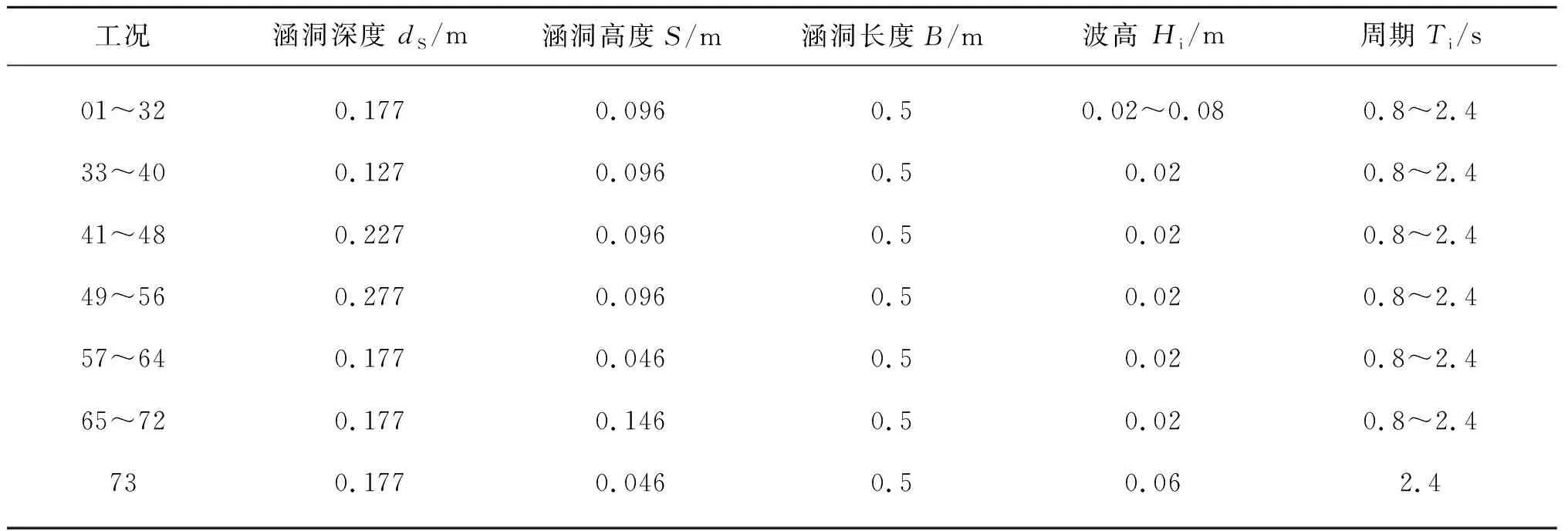
表1 模型试验以及CFD模拟工况设置Tab. 1 Conditions of model experiments and CFD simulations

2.2 CFD数值模拟布置

CFD数值波浪水槽布置见图2，水槽布置与模型试验布置基本一致。但数值水槽另外在14.25 m处设置流速测点FV1，用来监测整个涵洞断面的水平流速u(x,z)，进而计算出整个断面的振荡流量Qn；同时，在0～4 m处设置波浪造波松弛区，用来吸收从结构物传来的反射波浪，18～26 m设置为消波区。数值模拟工况与模型试验一致，具体见表1。

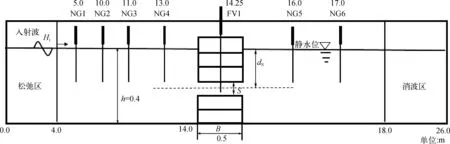
图2 数值波浪水槽示意Fig. 2 Schematic diagram of a numerical wave flume

2.3 模型验证

为验证数值模拟的正确性，需将数值模拟结果与试验结果进行对比。图3表示在涵洞深度dS=0.177 m，涵洞高度S=0.096 m 的条件下，CFD结果与试验结果的波面曲线对比，其中图3(a)表示波高Hi=0.08 m,波周期Ti=1.57 s的波面对比，图3(b)表示Hi=0.02 m,Ti=1.98 s的波面对比。从图3中可以看出，图3(a)的波浪透射试验结果以及CFD模拟结果几乎一致，图3(b)的透射结果略微偏大主要是由于试验消波区略短，存在部分反射波与透射波的叠加，故随着时间的增长，透射值逐渐变大；反射结果两者略有差异，但整体差异不大。上述结果表明双液相VPM-THINC/QQ模型能较好重现实际波浪与涵洞式防波堤的相互作用，具有一定可靠性。

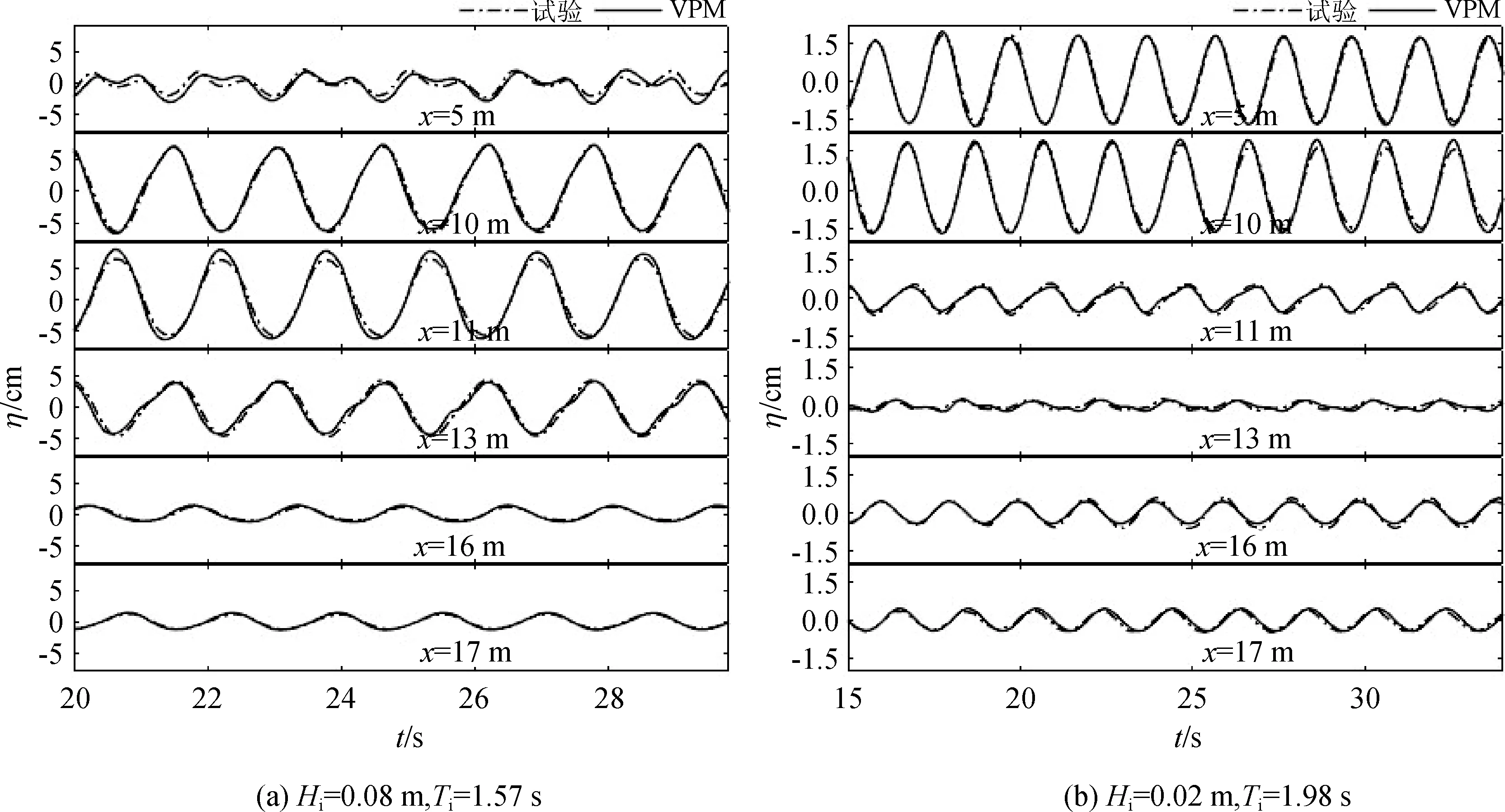
图3 试验及CFD波面对比(dS=0.177 m,S=0.096 m)Fig. 3 Comparisons of experimental results and CFD wave surface (dS=0.177 m,S=0.096 m)

为分析涵洞内部水体输移规律，试验中，涵洞内部水体用染色剂进行染色。该部分染色水体在一段时间内，能定性的反映出波浪作用下的水体运动规律。图4表示在波高Hi=0.06 m，周期Ti=2.4 s，涵洞深度dS=0.177 m，涵洞高度S=0.046 m条件下试验与数值模拟的涵洞内部水体输移轨迹对比。图4(a)、4(b)分别表示初始时刻以及波浪运动初期数值模拟条件下的双液相水体分布情况；图4(c)、4(d)分别表示初始时刻以及波浪运动初期试验条件下的染色水体分布情况。从图4中可以看出，当波浪传到结构物时，涵洞内部水体在波浪的作用下会向防波堤内侧输移，并在涵洞口形成近乎对称的两个涡旋，逐渐把涵洞内部水体带出。对比试验与数值结果发现，两者现象几乎一致，涡旋轨迹及大小也近乎相同，表明双液相模型能够较好地模拟出波浪作用下的水体输移规律。

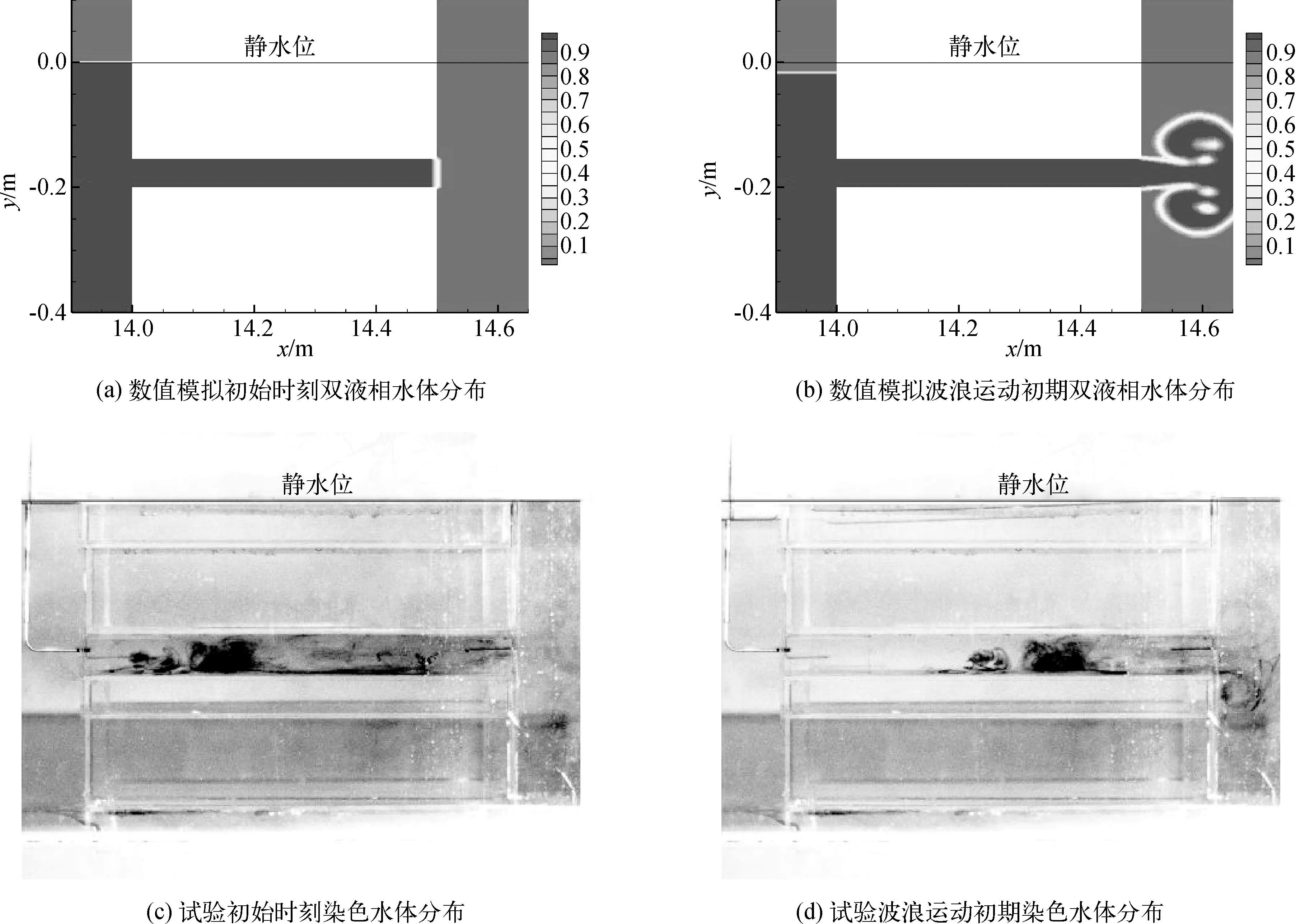
图4 双液相验证(Hi=0.06 m,Ti=2.4 s ,dS=0.177 m,S=0.046 m)Fig. 4 Verifications of two-liquid phase (Hi=0.06 m,Ti=2.4 s ,dS=0.177 m,S=0.046 m)

模拟与试验结果对比表明，文中所提出的双液相VPM-THINC/QQ模型能够真实反映波浪作用下涵洞式直立堤的水体交换特性。

3 结果与讨论

由于已经验证文中数值模拟能够较好重现波浪与涵洞式直立堤的相互作用，故下文结果均为数值所得。为探究涵洞式直立堤的水体交换特性，定量分析涵洞内部的流体运动规律，定义涵洞内14.25 m处的水平振荡流量Qn如下：

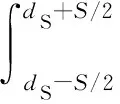
(11)

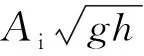
3.1 涵洞内水体交换的机理分析

为分析涵洞式直立堤的水体交换机理，通过分析涵洞附近的双液相分布、涡量分布以及流线分布规律对其展开研究。其中双液相为了揭示涵洞式直立堤的水体交换作用，涡量分布用来说明波浪与防波堤作用机理，流线分布则是涡量的一个补充，用来说明涵洞内部水体的振荡规律。图5、6表示波浪与结构物作用稳定后，不同周期的4个典型相位下(时间间隔为Ti/4)双液相分布、涡量分布以及流线分布。

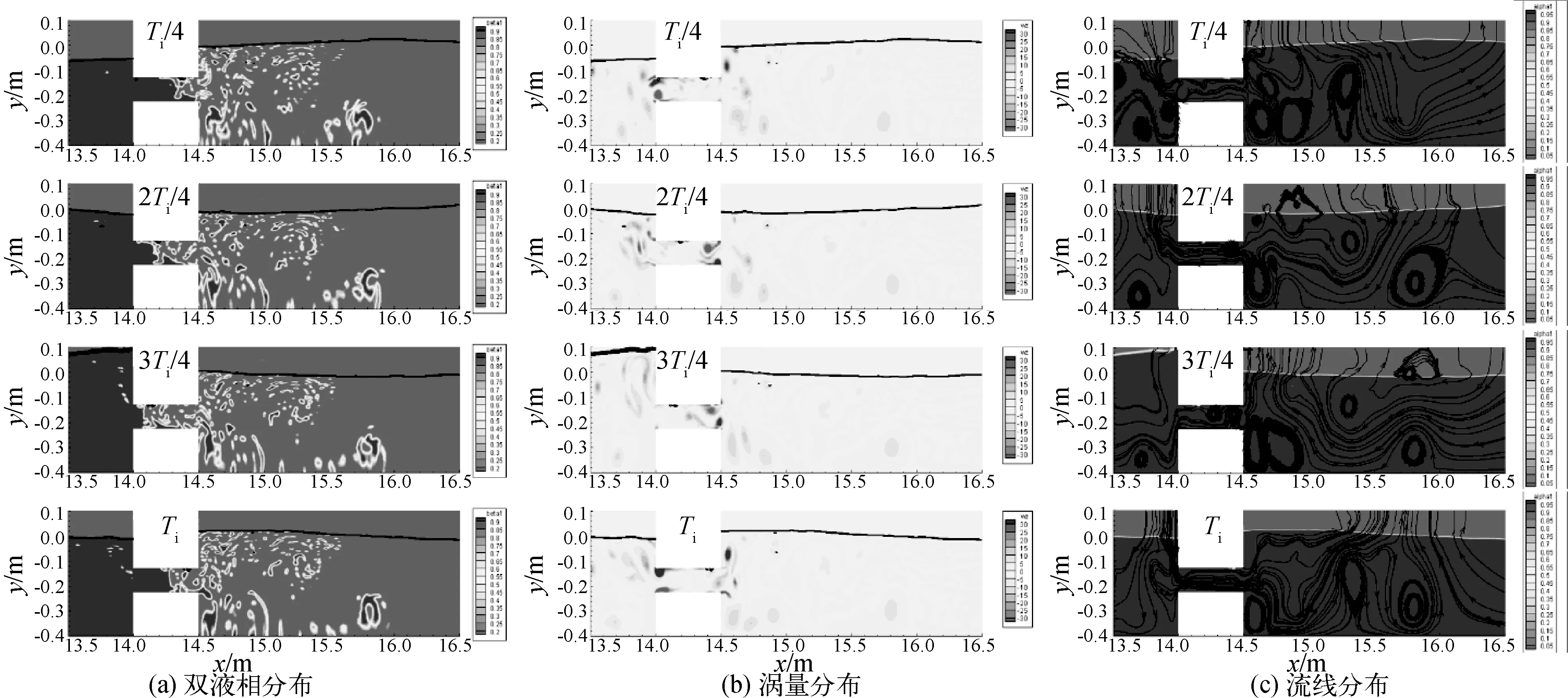
图5 一个周期内涵洞内部水体交换特性(Ti=2.40 s,Hi=0.08 m,dS=0.177 m,S=0.096 m)Fig. 5 Water exchange characteristics inside the culvert in a period (Ti=2.40 s,Hi=0.08 m,dS=0.177 m,S=0.096 m)

图5的试验条件为波周期Ti=2.40 s，波高Hi=0.08 m，涵洞深度dS=0.177 m，涵洞高度S=0.096 m。由图5可看出，自入射波从波谷到达波峰的半个周期内(图5(a))，港池内侧出现了未染色水体而港池外侧出现部分染色水体，表明涵洞内部以及港池内侧(透射波方向)水体逐渐被带入港池外部(来波方向)，期间水体大量掺混，涵洞内外水体发生交换。对比涡旋轨迹(图5(b))能发现，当堤前波浪处于波谷时，涵洞入口(来波方向)附近会形成上下两个涡，涵洞出口(透射波方向)水面以及水底附近也会形成涡旋。此后，在波浪从波谷到波峰的运动过程中，涵洞入口附近的两个涡逐步被带到堤前水面附近，并逐渐消散，同时带走了大量涵洞内部的水体；而防波堤外侧水面及水底附近的涡逐渐运动到涵洞出口处，并进入涵洞。观察流线图能发现，涵洞内部流线较为平顺，仅在波浪转向(波峰、波谷)时内部流线发生改变，表明在波浪与其作用的过程中，整个水体交换在半个周期内(波峰到波谷，或者相反)是稳定而平顺的，在整个周期内则是呈现出振荡的特性。当入射波从波峰到达波谷的半个周期内，涵洞内部以及港池外侧水体逐渐被带入港池内部，对比涡旋轨迹能发现，此时涡旋运动规律与波谷到波峰时的规律相反。堤前水面以及水底形成的涡逐渐运动到涵洞内部，而涵洞出口附近的涡则逐渐被带入到水面以及水底附近。上述结果表明，涵洞内部水体在波浪的驱动下，往复环流，形成一股振荡的水流，进而完成水体交换。在此过程中，虽然单次波浪周期所完成的水体交换量不算太大，如图5的双液相可以发现港池外侧逐渐出现港池内测的水体，但在长时间的波浪作用下，水体交换范围将逐渐扩大，进而可以较好地实现港池内外水体交换的目的。

图6试验条件与图5类似，只是波周期变为1.18 s，可以看出，其分布规律与长周期大体相似，但仍有一定差异，主要体现在水体交换强度弱于长周期波浪，同时，涵洞附近的涡脱轨迹也有一些不同。主要由于，在短周期波浪作用下，水体垂向能量部分不均匀，水面附近能量远远大于水底，故涵洞入口处仅在涵洞上部形成涡，而后逐渐被带入到水体表面，如此来回振荡；涵洞出口处与长波类似，形成上下两个涡，但由于透过波能较小，其运动轨迹远远小于长波，仅在涵洞出口附近来回振荡。波浪作用下涵洞内部的流线分布规律几乎一致。

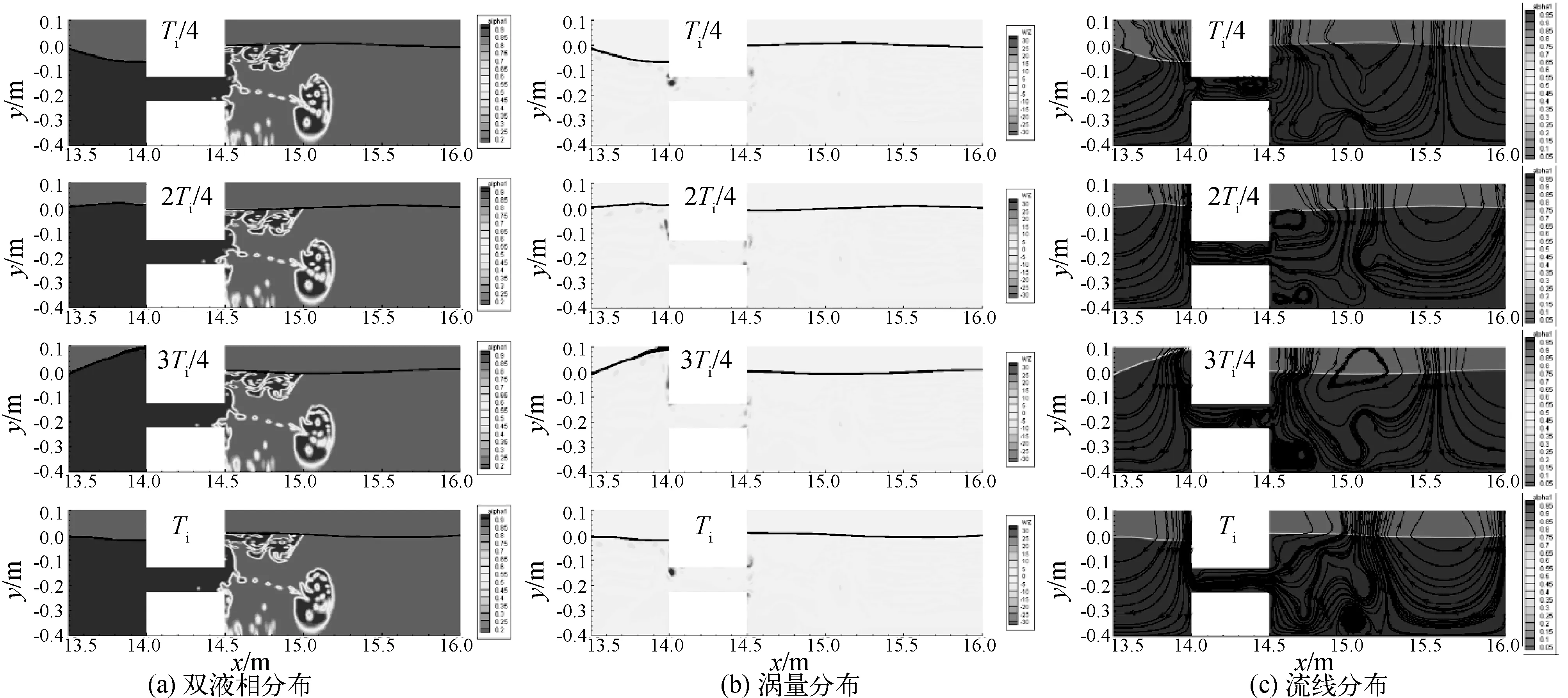
图6 一个周期内涵洞内部水体交换特性(Ti=1.18 s,Hi=0.08 m,dS=0.177 m,S=0.096 m)Fig. 6 Water exchange characteristics inside the culvert in a period (Ti=1.18 s,Hi=0.08 m,dS=0.177 m,S=0.096 m)

3.2 涵洞参数对水体交换的影响

图7表示当波高Hi=0.02 m，涵洞深度dS=0.177 m时不同涵洞高度S下的涵洞内部振荡流Qn随时间t的变化曲线，图7(a)、7(b)分别表示波周期Ti=1.00 s、Ti=2.40 s时的Qn变化曲线。从图7中可以看出，Qn随t正弦变化；随着S的增大，Qn在短周期下随着高度的增长近乎同比例增大，在长周期下，增大倍数略小于高度增长率。

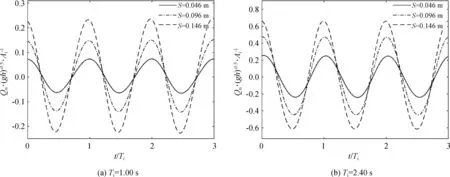
图7 涵洞高度对涵洞内部振荡流Qn的影响(Hi=0.02 m,dS=0.177 m)Fig. 7 The effects of the culvert heights on the oscillatory flow Qn inside the culvert (Hi=0.02 m,dS=0.177 m)

图8为当波高Hi=0.02 m，涵洞高度S=0.096 m时不同涵洞深度dS下的涵洞内部振荡流Qn随时间t的变化曲线，图8(a)、8(b)分别表示波周期Ti=1.00 s、Ti=2.40 s时的Qn变化曲线。从图8中可以看出，随着dS的增大，短周期下的Qn不断变小；长周期下的Qn也在变小，但变化幅度很小。主要由于短周期波浪能量集中于水面附近，越靠近水面，涵洞所能透过的波能越多，进而Qn变大；而长周期下的波浪水质点速度整个垂向分布较为均匀，改变涵洞位置对Qn的影响不大。

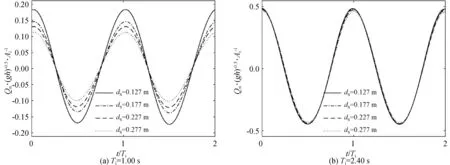
图8 涵洞深度对涵洞内部振荡流Qn的影响(Hi=0.02 m,S=0.096 m)Fig. 8 The effects of the culvert depths on the oscillatory flow Qn inside the culvert (Hi=0.02 m,S=0.096 m)

上述结果表明，增大涵洞高度能够明显地提高涵洞内部的流量，促进水体交换；减小涵洞深度对短周期波浪能够一定程度上提高涵洞内部的流量，但对长周期波浪作用很小。

3.3 波浪参数对水体交换的影响

由前文可知，在小波高情况下，涵洞内部振荡流随时间呈现出正弦变化，可以将其表示为Qmaxcos(σt)，其中Qmax为振荡流振幅，σ为波浪圆频率，t为时间。故在一个周期内涵洞内部水体的总输移量(周期积分)等于0。所以应该考虑的是半个周期的平均净流出，而半个周期的平均净流出流量Qave与振荡流振幅存在线性关系：

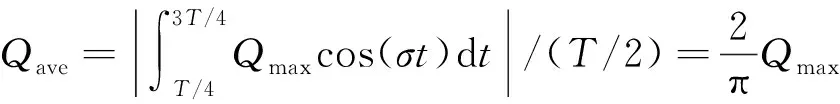
(12)

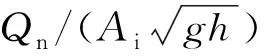
图9为在波高Hi=0.02 m，涵洞高度dS=0.177 m，涵洞深度S=0.096 m条件下，不同波周期Ti下涵洞内部振荡流频谱。

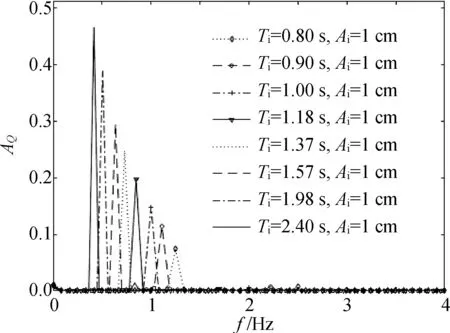
图9 不同波周期下涵洞内部振荡流频谱(Hi=0.02 m,dS=0.177 m,S=0.096 m)Fig. 9 Spectrum of the oscillatory flow in different wave periods (Hi=0.02 m,dS=0.177 m,S=0.096 m)

可看出，随着Ti的增大，振荡流基频振幅AQ不断增大；除了基频振幅外，涵洞内部存在部分倍频项，但倍频振幅较小，与基频振幅相比几乎可忽略。同时，发现波周期Ti=2.40 s (kh=0.55,k为波数,h为水深) 所对应的基频振幅约为Ti=0.80 s (kh=2.55)的7倍。上述结果表明，波周期对水体交换有较大影响，长周期波浪的振荡流量远远大于短周期波浪。

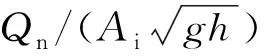
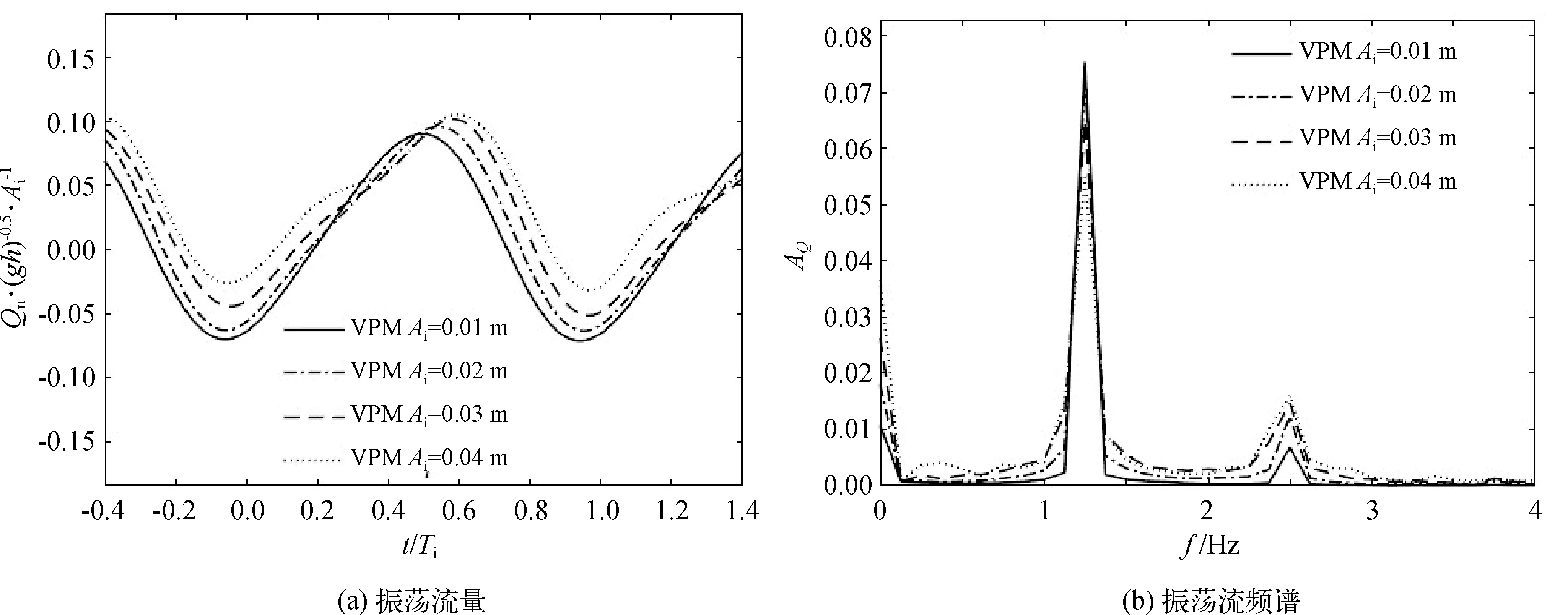
图10 波高对涵洞内部振荡流的影响(Ti=0.80 s,dS=0.177 m,S=0.096 m)Fig. 10 The effects of wave heights on the oscillatory flow inside the culvert (Ti=0.80 s,dS=0.177 m,S=0.096 m)

图11为50 s后不同波高下的双液相水体分布范围。可见随着波浪波高的增大，水体交换范围明显扩大；当作用时间足够时，水体交换能够逐渐扩散到整个港区，进而提高水体质量。上述结果表明，涵洞式直立堤在波浪作用下能够有效地实现港池内外的水体交换。

图11 50 s后不同波高的水体交换对比(dS=0.177 m,S=0.096 m)Fig. 11 Comparisons of the water exchange at different wave heights after 50 s (dS=0.177 m,S=0.096 m)

4 结 语

在VPM-THINC/QQ模型的基础上，提出一种能够标记涵洞内外水体变化的欧拉两相VOF方法，并结合物理模型试验，开展了波浪作用下涵洞式直立堤水体交换特性的研究，得到如下结论：

1) 基于VPM-THINC/QQ算法的双液相VOF方法能够较好反映真实流体的内部流动，具有较高的精度。

2) 涵洞内部水体交换机理如下：当防波堤堤前波浪从波谷向波峰运动时，涵洞入口处和涵洞出口的水面以及水底附近形成涡旋，带动涵洞内部水体向堤前运动；当堤前波浪从波峰向波谷运动时，涵洞入口的水面附近和涵洞出口处形成涡旋，带动涵洞内部水体向堤后运动。故在波浪作用下，涵洞内部会形成往复的振荡流，且该振荡流主导着港池内外的水体交换。

3) 涵洞高度对涵洞内部振荡流有较大影响；涵洞深度对短周期波浪有较大影响，而对长周期波浪影响不大；随着波浪非线性的增强或波周期的增大，涵洞内外水体交换作用加强。同时，随着非线性的增强，涵洞内部存在一个类似于斯托克斯漂移的净输移。在波浪长时间的作用下，涵洞式直立堤能够有效地促进港池内外水体交换。