基于深度学习的随船波浪测量技术研究

张建宏，卢文月，李 欣，田新亮，郭孝先，张显涛

(1. 上海交通大学 海洋工程国家重点实验室，上海 200240； 2. 上海交通大学 三亚崖州湾深海科技研究院，海南 三亚 572025)

浮式海洋平台是海洋资源生产活动的重要支撑，海洋平台的作业安全是各类海洋活动有序进行的前提。波浪作为海洋环境中最重要的环境要素，其测量工作是浮式平台水动力响应研究中十分关键的技术环节[1]。目前，对于平台所处海域海洋波浪测量的最主要手段为波浪浮标和X波段雷达，其中X波段雷达仅能够获得一段时间内波高与周期的统计值，而波浪浮标不能适用于深水环境且无法随船实时测量[2-4]。因此寻找新的技术手段实现波浪时序的随船测量成为浮式平台水动力响应研究中需要考虑的重要问题。

鉴于常规的测量手段对复杂实海域条件下浮式平台所处位置真实波面升高的实时测量难度较大，根据浮式海洋平台与波浪相互作用的机理，对平台气隙—运动响应数据进行推算进而获得高精度波浪时序信息。气隙响应及其预报方法对于波浪时序随船测量技术的研究十分重要，近年来众多学者通过理论研究的方法开展了气隙预报方面的研究。对于浮式结构物如半潜式平台来说，在平台设计阶段气隙响应的预报是一个十分复杂的问题，与许多参数有关，包括平台的主体特征，系泊系统的动力特性及海洋环境的特征等[5]。在平台实时监测中瞬时气隙响应主要受两部分影响：平台所处位置处的波面升高，平台的垂向运动响应。除此之外，气隙的动态变化还受入射波浪的非线性作用，涉及到波浪在平台立柱之间复杂的绕射、反射作用以及平台运动兴波的影响，这种绕射和辐射波浪叠加在随机入射波浪上会使得局部波面升高显著增加从而减小平台的气隙[6]。另外，入射波与平台立柱相互作用时存在的波浪—结构物水体共振现象，会造成局部瞬时波面升高，加上平台系泊及立管系统的影响，大大增加了气隙预报的难度[7-8]。采用线性分析理论远不能满足计算精度的要求,而二阶散射方法虽然可以提高计算精度，但是会过高估计气隙极值，其计算结果与试验结果存在一定的差距，并不能准确预报波面升高和波浪爬升的问题[9-11]。完全非线性的求解方式虽然能够较为精确预报平台的气隙分布，但因其理论模型复杂，计算量巨大，且波浪与平台、锚泊和立管系统之间的全耦合运动大大增加了计算难度，整体预报十分困难[12]。

为确定平台在不同极限环境条件下的水动力性能尤其是关注平台各位置处的气隙分布，模型试验是目前可以准确测得随机波浪下气隙时历的最常用方法。Mavrakos等[13]通过一座四立柱的浮式平台开展了一系列规则波试验，通过分析试验结果认为Nielsen等[14]计算出的波浪极端非线性现象在立柱周围尤为明显，且采用线性绕射和辐射理论很难模拟出此非线性现象，而锚泊状态下平台的垂荡运动降低了波浪的相对波面升高值。Naess等[15]对安装在挪威海域的Kristin半潜平台开展模型试验研究，分别使用三参数Weibull方法和Naess-Gaidai方法，利用模型试验测得的气隙时历建立统计修正模型，对半潜平台周围的极限波面升高进行准确统计，研究表明后一种方法在半潜式平台气隙预报方面更有优势。Lu等[16]通过一座三立柱半潜式平台的模型试验对其波浪爬升和气隙响应进行了研究，通过小波分析发现极端海况下气隙响应中的高频成分主要来自于入射波、平台的垂荡运动以及纵摇运动之间的耦合运动。除此之外，半潜式平台气隙响应的实船监测也是国内近年来逐渐开展的研究方向，盖晓娜等[17]对安装在中国南海的一座半潜式平台上的传感器在一年中采集到的气隙数据进行了时域分析、谱分析和统计分析，提出了一些经验性的实测气隙数据分析方法。

针对浮式平台所处海域波浪—结构物非线性相互作用以及传感器测量位置偏移导致的测量误差，利用半潜式平台模型试验获得的气隙和运动响应数据集，引入深度学习的方法对波浪—结构物相互作用过程中复杂非线性问题进行建模，开展入射波浪时序测量方法的研究。深度学习和神经网络技术也在近年来被国内外学者用来解决海洋工程水动力响应方面的预测、解算等问题[18-22]。

1 气隙响应数学模型

1.1 气隙的定义

气隙定义为海洋平台下层甲板底部至波面间的垂直距离，平台的静气隙又称为初始气隙，被定义为下层甲板至静水面的垂直距离。平台的静气隙是在平台设计过程中根据极限设计状态所能允许的最小气隙值推算得出的重要设计因子，而实时气隙响应可以用来衡量波浪是否发生砰击、越浪等强非线性现象，甚至是否会对平台结构造成破坏。

图1表示平台分别在静水面和在波浪作用下的气隙现象。在静水中某一特定位置(x,y)的静气隙定义为a0(x,y)，这一距离是在平台设计过程中通过静水力计算确定的。在波浪作用的情况下，η(x,y,t)表示在t时刻，特定位置(x,y)处的真实波面升高；δ(x,y,t)表示平台在t时刻相对于静水状态，在入射波作用下在该点的垂向运动。

图1 平台在波浪中的气隙现象Fig. 1 The air gap phenomenon of the platform in the waves

半潜式平台的气隙响应瞬时值主要由两部分组成，一部分是平台某位置的真实波面升高值，即入射波信息；另一部分是平台的垂向运动。若平台在自由面上做小幅运动，则基于线性理论，平台实时气隙响应可以表示为：

a(t)=a0-[η(t)-δ(t)]

(1)

1.2 气隙—运动解算函数

考虑垂荡、横摇、纵摇运动对平台气隙响应的影响，以及非线性效应造成的误差对真实波面升高的推算过程带来的误差，则平台某特定位置处的真实波面升高可以表示为：

η(t)=a0+Heavep(t)-at(t)cos[ψ(t)]-εer(t)

(2)

式中：a0表示平台的静气隙，也称为初始气隙，表征平台下甲板至静水面的垂直距离，是平台设计阶段按照极限设计状态下平台所能允许的最小气隙值推算得出；at(t)表示测波微波雷达所测数值，由于实测中测波雷达安装位置是固定的，所以平台在波浪作用下产生横摇、纵摇等运动时测波雷达的测量值并不是该位置到波面的垂直距离；Heavep(t)表示平台气隙测量位置处的垂荡运动；cos[ψ(t)]表示平台由于波浪作用时平台的横摇、纵摇等运动对气隙测量的影响系数，由式(3)计算得到；εer(t)表示由于波浪—结构物之间的非线性效应造成的测量误差。

(3)

其中，Rollp(t)与Pitchp(t)分别为平台气隙测量位置处的横摇、纵摇运动。因此，为了更方便对真实波面升高进行精确预测，在不考虑波浪的非线性影响下，建立气隙—运动解算函数，以气隙响应和运动响应作为函数的输入值，对波面升高进行估算：

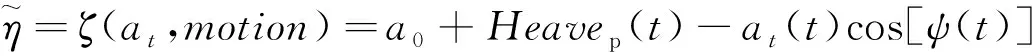
(4)

1.3 平台运动响应空间坐标变换

在海洋平台的气隙实际测量中，通过GNSS-INS组合定位技术获得的6自由度运动往往以平台重心位置(XCOG,YCOG,ZCOG)作为参考点。为了对平台气隙测点(Xp,Yp,Zp)处的真实波面升高进行推算，需要将平台中心位置的运动换算到气隙测点位置处的6自由度运动，可以通过空间运动坐标变换来实现：

(5)

其中，

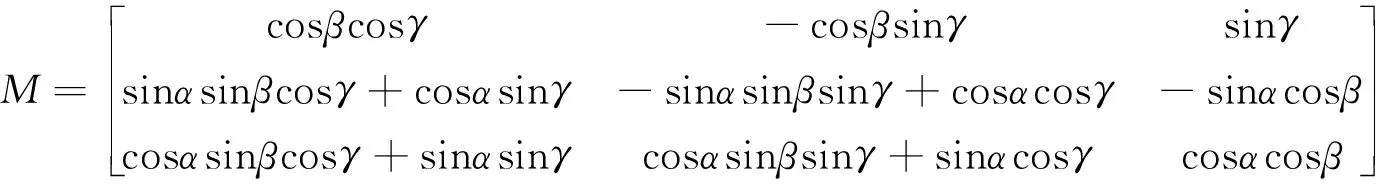
(6)

式中：α,β,γ分别是横摇、纵摇和艏摇；SurgeP，SwayP，HeaveP分别为船体在x,y,z方向的偏移。对于浮式半潜式平台，波浪—结构物水体共振是一种非常复杂的非线性现象，现有预报理论尚不能准确对其进行预报[8]。文中的波浪测量技术是其预报过程的逆过程，其内在机理更为复杂多变，因此利用深度学习技术强大的非线性映射能力，基于模型试验获得的平台6自由度运动数据和气隙数据，建立波浪测量的神经网络结构。

2 半潜式平台模型试验

研究依托在海洋工程深水试验池开展的陵水17-2半潜式平台模型试验，模型试验的缩尺比为1∶60，该模型的主尺度如表1和图2所示。

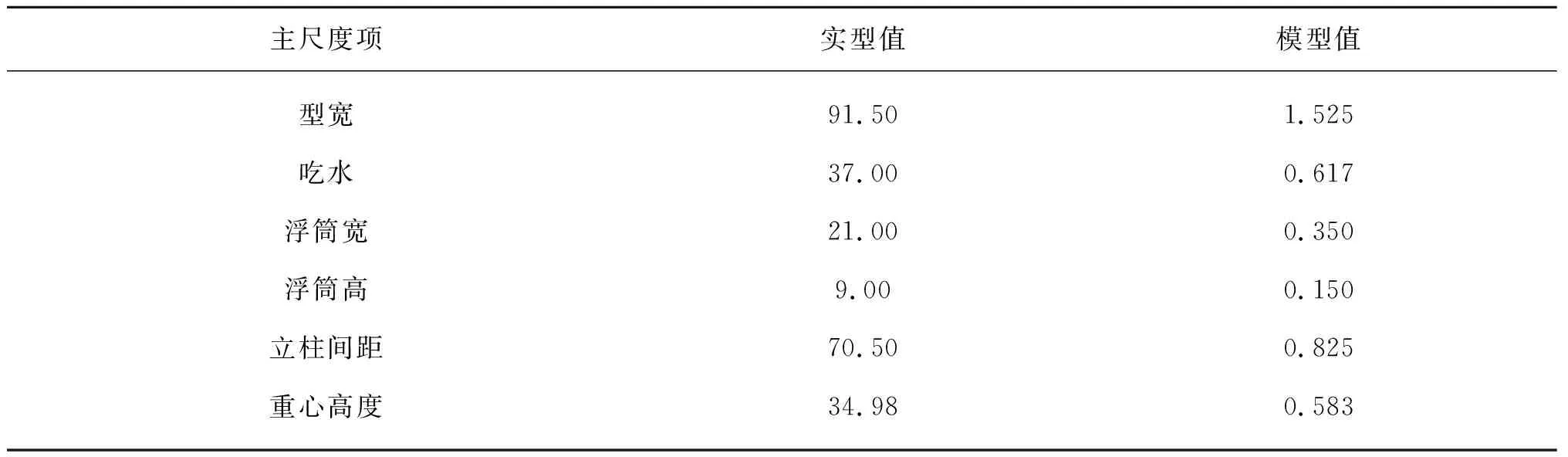
表1 陵水17-2半潜式平台主尺度Tab. 1 Main dimensions of LS17-2 semi-submersible platform (m)

图2 陵水17-2半潜式平台模型Fig. 2 The model of LS17-2 semi-submersible platform

针对陵水17-2半潜式平台依次开展了静态刚度试验、静水衰减试验、白噪声试验及不规则波试验，对不同极限海况下平台的水动力性能进行了研究[8]。试验过程中的不规则波均使用Jonswap波浪谱进行模拟和校核。选取其中两种不同海况开展随船波浪测量的研究和计算，其波浪参数如表2所示。

表2 不规则波参数说明Tab. 2 Description of irregular wave parameters

在试验校波阶段，水池中央180°迎浪方向安装的一组浪高仪用于测量水池中无结构物存在时该位置的真实波面升高，校波试验中的波面升高与目标值的谱分析对比如图3所示；在不规则波试验阶段，使用非接触式6自由度运动采集与分析系统，通过运动捕捉相机对固定在平台上的4个LED灯球构成的刚体进行识别从而获得平台在重心位置处的6自由度运动响应；通过在平台各位置处安装的电阻式浪高仪的测量，获得了平台不同位置处的实时气隙响应，试验现场如图4所示。

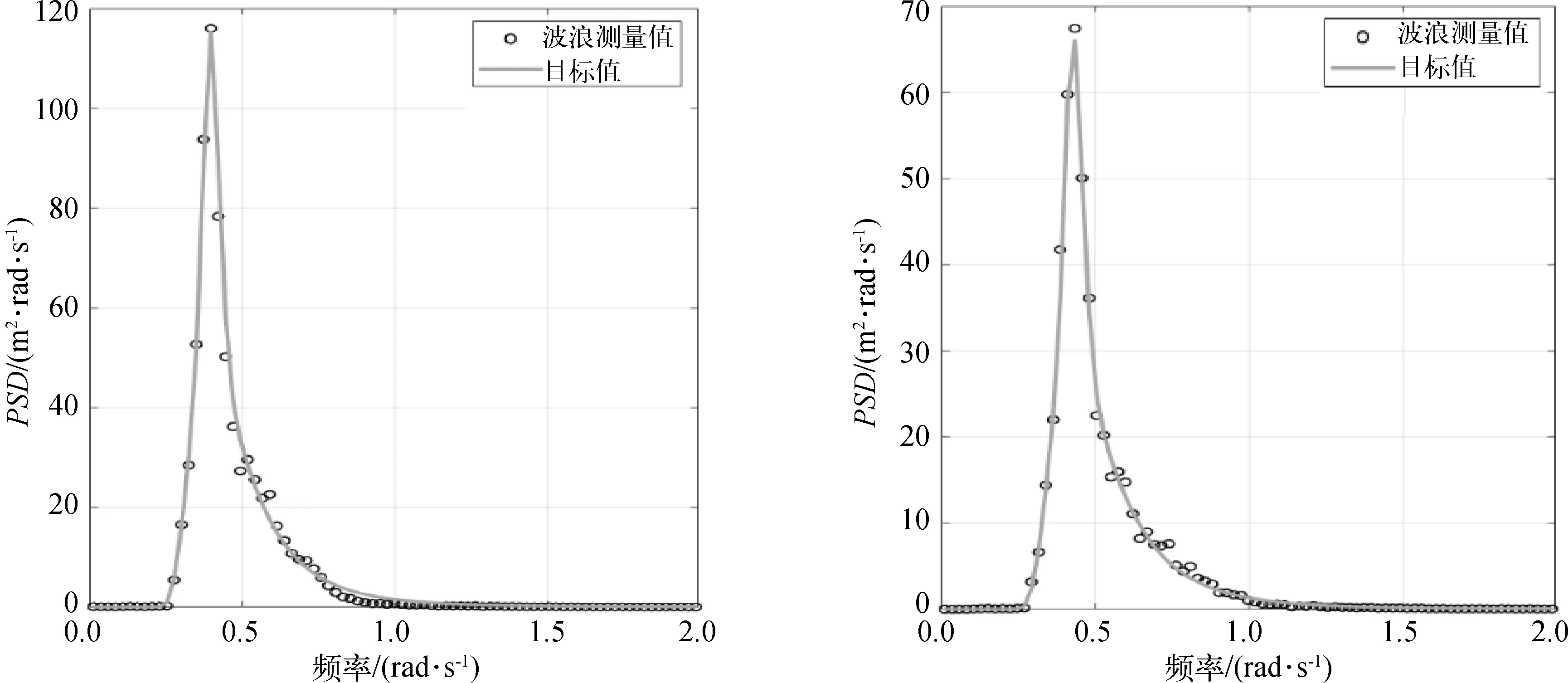
图3 校波试验的谱分析结果Fig. 3 Spectrum analysis result of wave calibration test

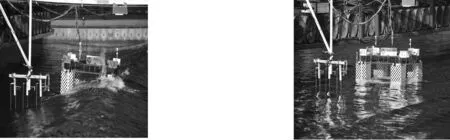
图4 平台在不同海况下进行不规则波试验Fig. 4 The platform conducts irregular wave tests under different sea conditions

试验过程中各传感器的采样频率均为60 Hz，试验结束后对两种不同参数的不规则波试验的气隙、运动响应及目标真实波高数据分别进行了滤波。在试验过程中，校波阶段测得真实波面升高与基于有结构物时的波面升高测量结果并非同步测量，但由于其浪高仪位置均在平台迎浪方向的中轴线上且十分相近，所以二者数据同步可以利用数据分析软件通过相位调整实现。根据波浪作用于半潜式平台的气隙响应机理，利用气隙—运动解算函数，利用试验中所得气隙响应和运动响应(主要是垂荡、横摇和纵摇运动)作为输入，对平台下层甲板某特定位置处的波面升高进行计算。

3 基于深层神经网络的波浪时序算法

深层神经网络是从结构、实现机理和功能上都对生物神经网络的一种近似和模拟，由大量神经元通过复杂连接构成的自适应非线性动态系统，无需事先确定输入与输出之间的映射关系，仅通过自身训练学习某种规则，在给定输入值时获得最接近期望输出值的结果[23]。反向传播(BP)神经网络是一种按误差反向传播算法训练的多层前馈网络，其算法为BP算法，它的基本思想是梯度下降法，利用梯度搜索使神经网络的实际输出值与期望输出值的均方误差最小[24]。BP网络可以应用于随船波浪预测的研究中，利用神经网络的强大非线性映射能力取代了入射波与平台相互作用中波浪复杂非线性效应的理论模型，仅以半潜式平台模型试验的气隙—运动解算函数的波高估计值和平台运动响应作为输入，目标真实波面升高作为输出就可以对神经网络实现网络参数的优化过程，从而训练出可以精确推算出平台所在位置处波浪时序信息的神经网络模型。

定义一个映射f：Ia,Im→η，其中Ia表示半潜式平台某位置的气隙响应，Im表示平台的6自由度运动，η表示气隙测点处的真实波面升高。训练数据集向量组用{(Ia1,Im1;η1),(Ia2,Im2;η2),……,(Ian,Imn;ηn)}来表示，用于模型训练的数据集时长为1 394 s，对应实尺度下的3 h，经过气隙—运动解算函数的解算后，作为输入和输出对模型进行训练。

图5为整个随船波浪预测研究过程的示意，主要包括3部分内容：1)模型试验，波浪通过输入造波信号，驱动水池前端的摇板造波机产生，在造波板的对岸安装消波滩以消除波浪反射对试验区域波动场的影响，通过传感器及运动采集系统获得研究所需的数据集；2)数据预处理过程，将获得的气隙及运动响应数据进行相位修正、滤波等处理后，利用气隙—运动解算函数获得波面升高的初步计算值；3)深层神经网络模型训练过程，利用前序步骤预处理后的输入数据，以校波过程中的真实波面升高作为目标值计算损失函数，对神经网络中的参数进行更新、优化。

图5 随船波浪测量技术的流程Fig. 5 Flow chart of onboard wave measurement technology

在训练开始前，对所有数据进行了归一化处理，目的是消除平台不同响应间由于本身数量级的差异而对训练优化过程造成的影响。

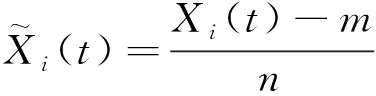
(7)

其中，m和n分别为对应输入数据Xi(t)在30 min时间序列的平均值和标准差，在研究中均为常数，统计值见表3,其中m1,n1分别代表工况1(Hs=16.9 m,Ts=15.9 s)对应输入数据的均值和标准差。

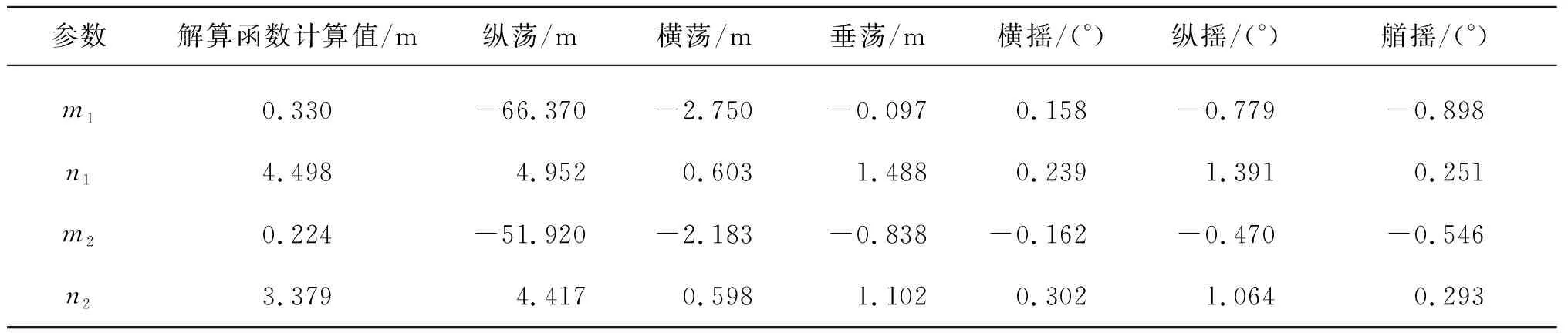
表3 输入数据的均值和方差Tab. 3 Mean and variance of the input data

预处理后的数据集在训练之前被划分为训练集和测试集，其中将工况1和工况2模型试验数据集合并后的前70%数据用于训练，后30%数据作为测试集。在训练过程中，由于学习率的敏感度对模型的性能有显著影响，选择了自适应学习率算法RMSProp[25]，这一算法对神经网络的参数梯度使用微分平方加权平均数进行更新，训练中初始学习率设置为0.001，并采用均方误差MSE作为训练中的损失函数。

为了减少训练过程中个别异常数据对神经网络参数的影响，在随机梯度下降优化中，采用了小批量随机优化方法，批量样本数为8。

4 波浪预测结果及验证分析

4.1 气隙—运动解算函数对真实波面升高的估计结果

根据刚体运动及空间坐标变换理论，考虑平台垂荡、纵摇、横摇等运动对气隙的影响得到平台甲板底部位置处的垂向运动，建立气隙—运动解算函数即可对该位置处的波面升高做出初步计算。

基于波浪—结构物相互作用的气隙理论，利用气隙—运动解算函数获得波面升高的计算值，这一解算过程主要是将平台的垂向运动对气隙响应的贡献减去，图6分别给出了气隙—运动解算函数计算波高和真实波面升高的时序结果和谱分析结果。对比显示，解算波高结果与该位置的真实波面升高在时域和频域上均存在一定的误差，这主要是由于未考虑波浪与平台作用的辐射、绕射等非线性效应所引起的。如图6所示，平台气隙响应的频率有3个峰值，分别在0.15 rad/s、0.50 rad/s和0.70 rad/s附近。其中在0.15 rad/s附近，平台入射波浪在这一频率范围能量接近于0，而解算函数计算波高在这一范围内还有一个峰值，但这个峰值相比于气隙响应的峰值明显减小；在0.50 rad/s附近，气隙响应、解算函数计算波高及真实波面升高的能量都达到了最大峰值；在0.70～0.80 rad/s附近，气隙响应及解算函数计算波高有一个较大的峰值，并且二者的峰值比较接近。

图6 气隙—运动解算函数计算前后的时域和频域结果Fig. 6 Time domain and frequency domain results before and after the calculation by air gap-motion decoupling function

由于频率0.15 rad/s与平台的纵摇运动固有频率十分接近，说明除了垂荡运动的影响外，平台的纵摇运动对垂向运动影响的权重较大，这一现象在气隙响应的能量分布中有所体现，很可能是气隙浪高仪的安装位置在平台船艏中部位置处的原因。由前述校波试验的结果可知，0.50 rad/s是波频部分，在这一部分，解算函数计算波高相比气隙响应更接近真实波面升高；在0.70～0.80 rad/s附近，解算前后的谱峰几乎完全重合，说明从气隙中去除垂向运动对这一部分频率的能量几乎没有影响，这一频率范围存在的能量很有可能是由于波浪与平台相互作用中的非线性效应所产生，因此为了进一步减小波浪测量技术中存在的误差，考虑入射波与平台的绕射、辐射效应，采用深度学习的方法进行进一步研究。

4.2 基于深层神经网络对真实波面升高的进一步预测结果

分别利用深层神经网络对0°时Hs=13.4 m和Hs=16.9 m工况的真实波面升高进行预测，图7和图8分别展示了不同波高工况的时域预测结果。相比于气隙—运动解算函数的计算值，深度学习的波面升高测量值显著接近于目标真实波面升高值。

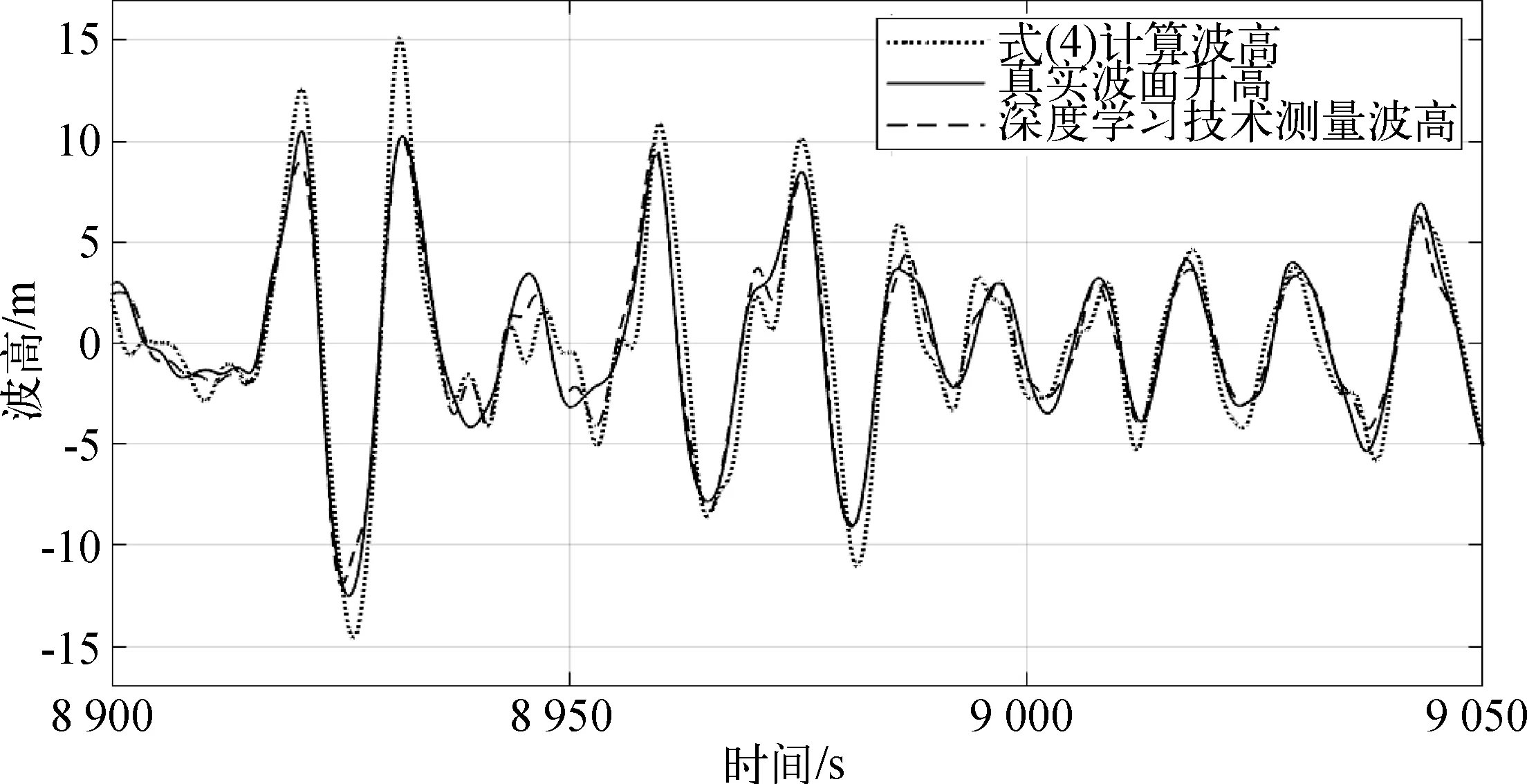
图7 随船波浪测量技术的时域预测结果(Hs=16.9 m,Tp=15.9 s)Fig. 7 Time domain prediction results of onboard wave measurement technology (Hs=16.9 m,Tp=15.9 s)

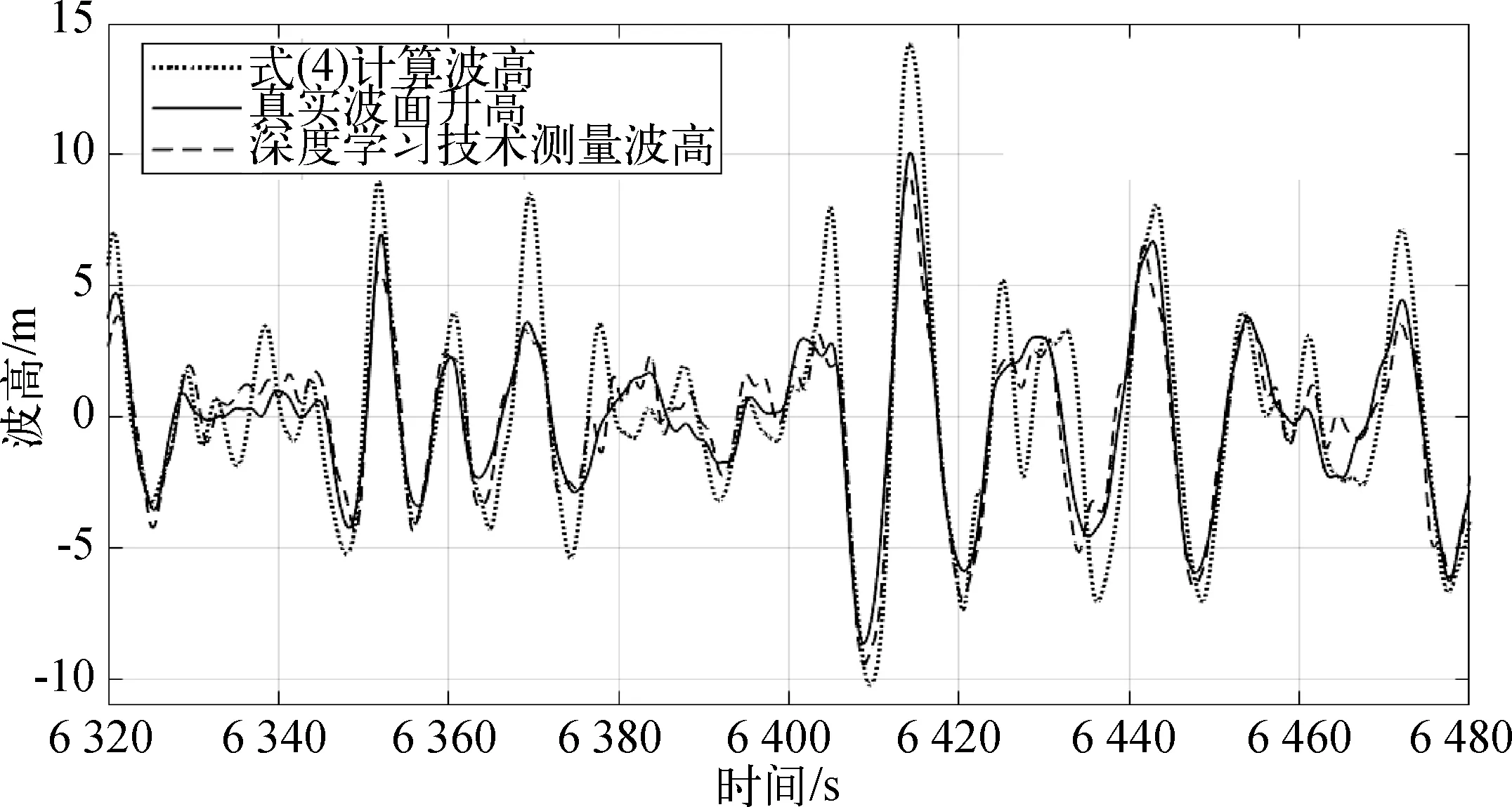
图8 随船波浪测量技术的时域预测结果(Hs=13.4 m,Tp=14.7 s)Fig. 8 Time domain prediction results of onboard wave measurement technology (Hs=13.4 m,Tp=14.7 s)

为检验深层神经网络是否能消除由于波浪的非线性效应所带来的误差，图9展示了神经网络训练前后的波浪时序及目标波浪时序的谱分析结果，可以看出经过深层神经网络预测后的波面升高相对于预测前的气隙—运动解算函数计算值，基本消除了波浪在0.50～0.80 rad/s范围内的波浪非线性特性，与目标波高的能量分布十分接近。这一结果表明了深层神经网络的非线性映射能力可以解决在波浪预测中遇到的复杂非线性问题。

图9 随船波浪测量技术测量波高与目标值的谱分析结果Fig. 9 Spectral analysis results of target wave height and the value measured by shipboard wave measurement technology

对训练前后波面升高时间序列的标准差进行了计算并比较，其结果如图10所示，可以看出利用深层神经网络模型训练后的波高，其时间序列的标准差相比训练之前的计算结果更接近真实波面升高。

图10 波浪测量技术测量波高与目标波高的标准差结果对比Fig. 10 Comparison of the standard deviation between the wave height measured by the wave measurement technology and the target value

5 结 语

提出了一种基于深层神经网络，利用平台测得气隙推算所在位置真实波面升高的波浪时序测量技术，该算法相比于线性推算方法显著提升了波面升高在时域和频域上的计算精度。分别选取百年一遇和千年一遇波浪工况下半潜式平台的气隙响应数据及运动响应数据进行神经网络的建模，计算结果表明神经网络模型计算波高时序相比于线性计算波高时序精度有显著提升；在谱分析中，深度学习方法计算的波面升高依旧消除了平台运动对波面升高低频部分计算造成的影响，并且显著消除了波浪—结构物非线性效应造成的波面升高高频部分误差，由此基于深度学习计算的波浪谱对比线性计算的波浪谱，与目标波谱在各频域范围内都更为接近；除此之外，对两种计算结果分别进行统计值计算并与目标值进行对比发现，深度学习计算波高与实际波高更为接近。然而，由于实际海域中极其复杂的风浪流环境及尺度效应的存在，以及考虑到入射波浪向的复杂性，通过水池模型试验数据训练出的随船波浪测量模型的适用性还需通过海上实测技术进行进一步研究和验证。