网联交通环境交叉口公交优先信号滚动优化模型

马成元 刘咏平 俞春辉 罗瑞发 朱际宸 张 振 杨晓光

（1.同济大学交通运输工程学院， 上海 201804；2.金溢科技股份有限公司， 广东 深圳 518000）

0 引言

随着车辆保有量的增加，城市交通拥堵问题日益严重。相关管理部门提出优先发展公共交通是改善城市交通状况，提高运输效率的有效手段[1]。公交信号优先（Transit Signal Priority， TSP）通过调整交叉口信号配时，从而提高公交的运行效率。然而，现有的TSP策略受限于感知条件，无法兼顾公交车辆与普通车辆的通行效率，同时信号调整手段较为单一，往往对交叉口运行造成负面效果。

近年来，随着网联交通的快速发展，实时准确地获取轨迹级车辆信息成为可能，因此TSP可以同时考虑公交车和其他车辆的效益[2]。此外，一些研究[3]需要设置公交专用道，而这会牺牲普通车辆的通行空间，浪费交叉口时空资源。在网联环境下，公交车和其他普通车辆的信息能够被获取，可通过动态优化信号配时保证公交车辆优先，无须设置公交专用道，提高公交优先控制的适用性。

因此，该文提出了一种网联交通环境下的交叉口公交优先信号优化混合整数线性规划（Mixed Integer Linear Programing，MILP）模型。模型无须设置公交专用道，降低了TSP对普通车辆不公平的负面影响。该文采用滚动优化策略，充分利用实时精准的网联车辆信息，适应动态的交通状态。

1 公交优先信号优化问题分析

在网联交通环境下的典型单交叉口公交优先信号优化场景如图1所示。十字交叉口的4个方向包括左转、直行和右转共12个流向，其中右转车辆不受信号灯干预。车道皆有渠化方向，且无须特别设置公交专用道，公交车辆与普通车辆皆可从任意车道到达。在该文的信号优化中，各左转与直行的流向代表一个相位（序号为k=1~8，如图1所示），相位的组合和相序不予固定。图中ω为车辆序号，在网联通信区域中的所有车辆状态信息（包括车辆距交叉口的距离x0ω，及车辆速度v0ω）皆可通过路侧单元实时获取，包括车辆位置、速度、方向和乘客数量。路侧单元需要动态设计信号计时并更新交通信号灯。为简化优化问题，假设车辆在进入感知区域前已进入所需要的车道，在感知区域内禁止变道。

实际交叉口信号控制中，信号配时需要随实时的交通需求进行适应性变化。因此，该文中的信号配时优化是随时间线滚动优化的过程。在每次信号优化中，路侧单元首先根据公共汽车和私人车辆的实时的交通状态，预测各进口道内车辆到达交叉口处（停车线）的时间，进而产生未来一定时长内最佳的适应性信号配时方案。在传统信号配时优化研究中，优化时间长度往往是根据周期确定的。然而，离散化的周期长度的概念可能会限制在长期连续时间内信号配时的全局最优解。因此，该文信号配时中排除信号周期的概念，采用固定的时长h作为优化时长。路侧中心需要每隔一段时间重新优化，生成下一时段内的信号配时。同时这也可解决进口道内车辆未来运动状态不确定性的问题，因为对越接近停车线的车辆，其到达交叉口时间的预测精度就越高，所以通过滚动优化可以不断修正之前优化中预测的偏差，提高算法鲁棒性。为了避免信号配时的突然变化对所有交通参与者的负面影响，在每次的优化模型中保留了上次优化中的部分信号配时。

2 公交优先信号优化模型

该文将某一时刻的单次公交优先信号优化问题建立为混合整数线性规划（MILP）模型，以灵活优化相位组合、相序及各相位绿灯时间，而不受限于固定的信号周期和相序。从以人为本的交通公平性角度出发，考虑普通车辆和公交车的差异，优化模型的目标设为最小化各交通参与者的总行程时间。

式中：wω为车辆ω上的乘客数量，TTω为车辆ω的行程时间。Ω表示交叉口感知通信区内各进口道内的车辆集合。通过该优化目标，公交车辆在信号配时中的优先级和公交优先对普通车辆通行效率的负面影响都得到了合理地考虑。

模型的决策变量是优化时间域h范围内的信号配时，记为Y。在该研究中，信号配时表示如下。

式中：k是对应相位序号如图1所示，K是所有相位的集合。在该研究的模型中，每个相位在优化时间域h内可能有多次绿灯时段，Nk则是相位k在优化中出现的总次数（下同）；表示第i次出现的相位k的开始和结束时间。为了保障交通安全，需要对MILP中的信号配时进行约束限制。对相位k的第次绿灯时长的结束时刻oki和下次绿灯开始时刻ui+1k，显然如下。

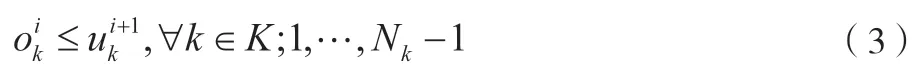
该模型中没有固定信号周期和相序的限制，只要满足以下安全约束条件，不同相位可同时绿灯。对2个冲突相位k1和k2（例如南向北直行和东向西直行），其绿灯必须要保持在最小绿灯间隔。另外，基于交叉口信号配时手册基本要求，各相位需要满足最大绿灯时长（设为）和最小绿灯时长（设为）的限制：

式中：tcω是车辆通过交叉口的时间，当前时刻t0。对各车辆的行程时间计算函数Hω（s0，Y）的解析表达，即模型目标函数与模型决策变量的关系，该模型考虑了车辆纵向行驶过程受到的对应相位的信号配时和其同时在进口道的前车的影响，具体函数形式可参考[4]。

另外，如上文所述，交叉口信号配时优化处于滚动执行的过程中，新执行的优化配时方案需要与上次的执行方案相衔接以保证控制稳定性。保留部分的信号配时需要在新的优化模型中加入以下约束：

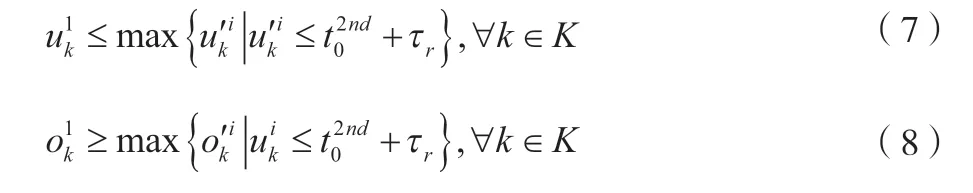
3 算例

该文基于图1中的场景建立SUMO微观仿真验证信号优化模型。实验中模型及算法采用C#实现，MILP模型使用求解器Gurobi 9.0进行求解，在配备Intel 3.60GHz CPU和16GB内存的设备上执行。模型求解计算时间在可接受的范围内，平均求解时间在2s内。单次仿真运行时间为1800s，预热时间为150s。

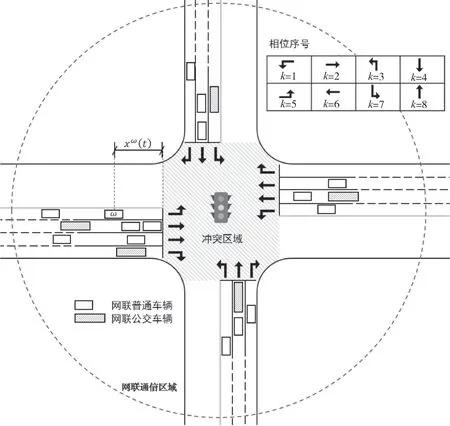
图1 网联交通环境下的公交优先信号优化场景

该文分布采用“车均”和“人均”的延误和通过量作为交叉口控制效率的评价指标。采用固定配时信号控制和传统基于事件响应机制的TSP方法（即，基于固定信号配时，公交车辆到达触发4s“绿灯延长”和“红灯早断”的公交优先信号策略）作为对照试验。在公交车和普通车辆混合交通的相同车辆到达情况下，对这3种控制策略进行了测试，实验结果如下所示。

3.1 车均/人均延误分析

在3种不同控制策略下交叉口的车均延误和人均延误如图2所示。2个指标的结果皆表明，该文中的滚动优化TSP方法明显优于其他2种信号控制方法。由于该文中模型对信号配时建模的高自由度，其他2种信号控制方法的信号配时方案包括在该文MILP优化模型的解空间中，因此在理论上滚动优化模型的控制效果是不劣于另外2种方案的。实际中，与其他2种方法相比，灵活的信号方案和频繁更新的滚动优化框架通常可以生成更优的信号控制策略来处理随机波动的交通需求。在图2（a）中，事件响应式的TSP方法会导致平均车辆延误的增加，尤其是在交通需求水平较高的情况下。这是因为其简单直接的信号调整策略完全由公交车到达触发，将牺牲其冲突方向的在交叉口的通行能力。而从交通公平性的角度出发，人均延误能更好地评价交叉口的服务水平。如图2（b）中所示，事件响应式的TSP控制方法有利于在交通需求不足的情况下减少人均延误，因为乘客数量更多的公交车具有优先权。当交通需求较大时，事件响应式的TSP往往会对整体效率带来严重的负面影响，导致所有交通参与者的出行时间较长。相比之下，所提出的滚动TSP控制方法利用实时信息以趋向全局最优，这将在考虑公交优先的同时考虑整体交通的通行效率。

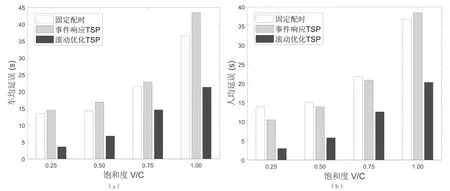
图2 3种信号控制策略下车均/人均延误比较

3.2 通过量分析

单位时间的通过量可以反映交通控制策略对交叉口时空资源的利用效率。图3和图4分别比较了3种控制方法的车辆和人员通过量。

如图3所示，交叉口车辆通过量在3种控制策略下随需求提高而增加。交通需求超过1500辆/h后，固定配时控制和事件响应式的TSP控制下的交叉口车辆通过量开始低于交通需求，即表示在这两种控制方式下已交叉口通行能力。其中，事件响应式的TSP控制下的通行能力略低于固定配时控制，同样是由于上述的响应式个体最优策略对系统效率的负面效应，而且在更高的交通需求下这种效应更加突出。而该文中的滚动优化策略，即使在交通需求超过2000辆/h后，车辆通过量仍在不断增加。实验表明，通过灵活而精准的适应性配时，滚动优化的TSP方法将提高交叉口通行能力25%以上。

图4进一步分析了人员通过量上3种控制策略的差异。总体趋势与车辆通过量特征一致，同时由于滚动优化模型中考虑了公交车辆在乘客数量的优势性，其控制效果的优势较图3更加突出。

图3 3种信号控制策略下人员通过量比较

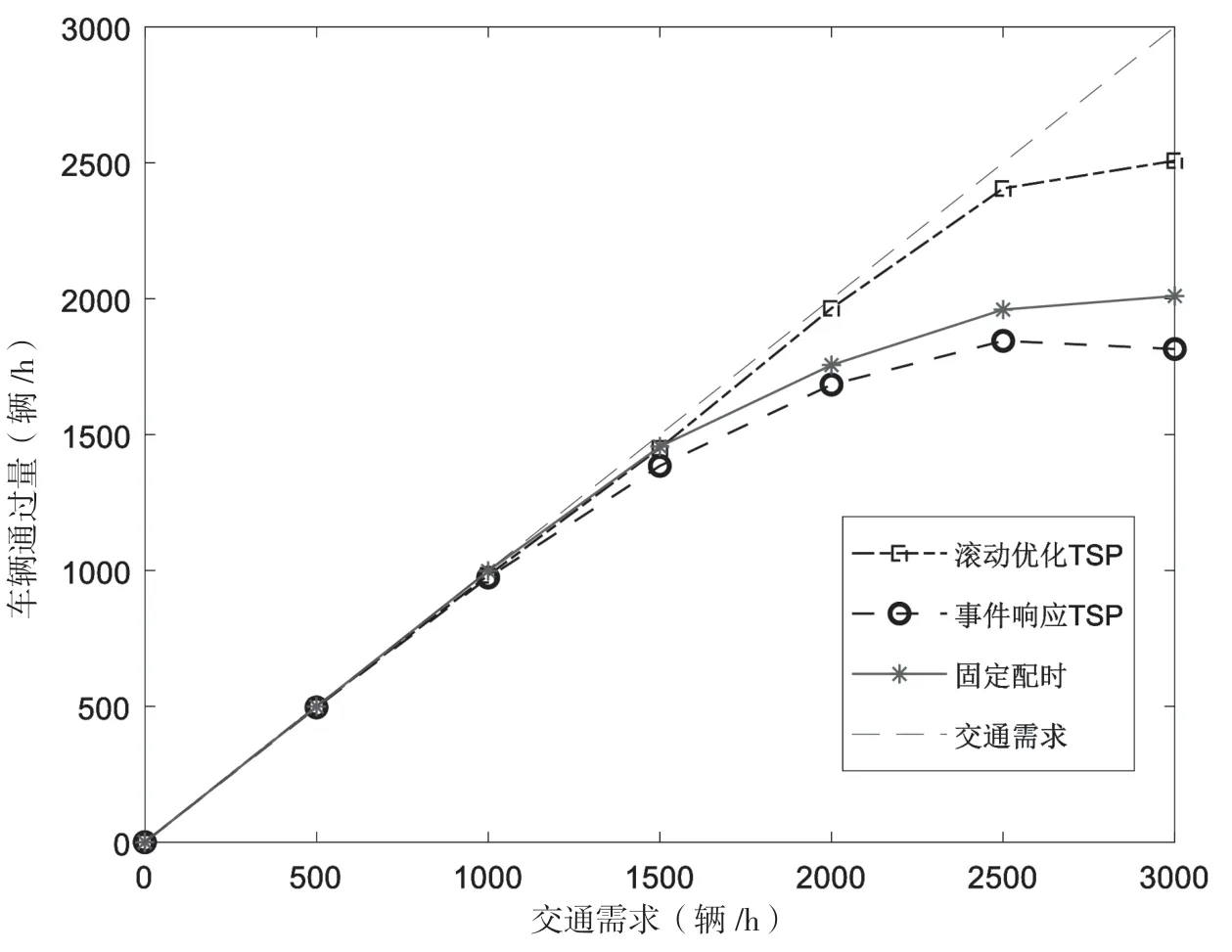
图4 3种信号控制策略下车辆通过量比较

4 结语

该研究提出了一种基于网联车辆实时数据的单交叉口公交优先信号配时滚动优化方法。建立了以所有出行者的总出行时间最小化为目标的MILP模型，采用灵活的信号框架，不限制信号周期及固定的相位组合和相序，并进一步提出了滚动优化执行框架。由于优化模型以全局最优为目标，因此信号配时在公交优先的同时不会对普通车辆的通行产生不公平的负面影响，灵活的信号策略和频繁更新的控制框架能够更好地适应动态变化的交通需求。仿真结果表明，与传统的事件响应式的公交优先方法相比，该文中公交优先信号配时优化模型可以显著减少所有需求水平下的车均及人均延误，同时可使交叉口通行能力提高25%以上。

该文中的模型在完全网联交通环境下建立，而实际城市交通中网联车辆难以大面积完全覆盖。下一步将在已有方法基础上，考虑存在非网联车辆的混合交通环境，提高模型的适用性。