基于AHP-粗糙集理论的冲击地压综合评价

梁燕华 李凌烜 成燕峰 刘 刚

（1.黑龙江科技大学电气与控制工程学院，黑龙江 哈尔滨 150022；2.黑龙江科技大学矿业与工程学院，黑龙江 哈尔滨 150022）

0 引言

冲击地压是一种对煤矿安全有重大威胁的煤岩动力灾害，对冲击地压的危险性进行评价是研究冲击地压的基础，而确定冲击地压各评价指标的权重变得尤为重要。曾振达等人[1]指出，层次分析法（AHP）受专家的水平和经验的制约，得到的结论主观性强且不稳定。王培等人[2]在研究粗糙集理论中提出，人们通常采用模糊理论、数据理论等数据处理方法处理海量数据等具有不确定性特征的信息问题，但由于需要先验知识，因此在实际操作中难以达到要求，而运用粗糙集理论则为解决该问题提供了新的思路与方法，可以更简便、有效地解决该问题。

该文分析冲击地压发生参量前兆（岩石应力、声发射信号的能量以及峰值频率等相关因素）并将AHP法与粗糙集理论相结合，运用AHP法确定冲击地压发生前兆的各类参数评价指标的主观权重，用粗糙集理论研究、分析数据并确定各类指标的客观权重，主观权重与客观权重相结合，使权重更加客观实际，对冲击地压事件发生概率的评价结果也更客观、更可靠。

1 冲击地压前兆特征相关理论分析

冲击地压应力前兆分析如下。应力是指当物体（煤岩）受到外力作用后发生形变，在形变过程中物体内相邻质点间的距离发生变化所产生的相关动力现象。而冲击地压事件的发生也必然受煤岩应力的影响；因此，应力也是常常被用来衡量冲击地压事件发生前兆的一类参量指标。通过分析与研究煤岩体所受应力大小的变化，可以有效地反映煤岩体整体的破裂程度。

在煤岩体加载初期-冲击地压事件发生前的一段时间内，煤岩的外表面会出现轻微的碎纹与细微的破裂，但是破裂的情况与裂纹的深度并没有突然增大的现象，因此煤岩内部所受应力较为平稳，变化不明显。随着时间推移，煤岩整体外部形变越来越大，煤岩内部质点间的活动加剧，应力不断转移集中，此时煤岩应力已开始加剧。当达到煤岩破裂的后期，破裂状况和裂纹深度进一步增大，在即将发生破坏的那一瞬间，应力也呈现急速增大的趋势，直到达到应力的峰值，该点可称为煤岩发生彻底破裂的前兆特征点，经过该点之后，煤岩所受应力进入失稳状态。当煤岩发生冲击地压之后，煤岩体内所受应力也逐渐呈现下降的趋势。

由于煤岩应力能够完整地反映煤岩体从平稳状态到破裂状态的变化过程。因此，提取煤岩应力作为表征冲击地压事件发生概率的一种特征参量。

声发射前兆特征分析如下。当煤岩受到外力作用的同时，岩体内部的微观结构也会发生变化。当岩体内部能量上升到所能承受的最大值时，此时的煤岩体结构最不稳定，而内部能量需要向稳定的状态下降过渡，在能量下降与释放的过程中，煤岩体外部发生变形、裂纹以及碎裂。在这一系列变化过程中，其中一部分能量要以应力波的形式进行释放，而这种以弹性应力波的形式释放应变能的现象就是声发射（AE）[3]。

在煤岩体发生相应形变与破裂的活动过程中，煤岩体外部形变和损伤就是通过该信号来表现的，因此对信号进行研究分析可以了解煤岩体整体外部形变过程，进而有效地对冲击地压进行预测。煤岩发生破裂的过程中，声发射特征参量的相关数值会按照一定规律不断地发生变化，

在煤岩体发生冲击地压前的一段时间内，煤岩的外部出现轻微的裂痕，但裂痕的深度与大小并未发生突然性的变化，此时声发射信号的波动较为平缓，变化较小，因此声发射振铃次数的值变化不大。随着煤岩体内的结构形变越来越大，煤岩整体碎纹也逐渐加深，煤岩内部质子结构活动不断加剧，煤岩体进入弹性变形阶段，此时声发射振铃计数的信号的变化迅速变大，急剧上升。在煤岩碎裂前段，其煤岩外表的破裂和裂纹进一步加深，相关的声发射特征参数（峰值频率、信号强度等）呈现瞬变式的增长，此时声发射信号的参量达到峰值。

声发射的特征信号会随煤岩载荷的加载而改变，而声发射的峰值频率可以对受力煤岩内部质子的活跃性进行评价，信号强度可以在煤岩受力至发生冲击地压事件的过程中反映信号整体的衰减过程，因此提取峰值频率与信号强度等声发射信号对冲击地压进行预测有较强的说明性与可行性。

2 AHP-粗糙集理论模型

2.1 粗糙集理论

2.1.1 粗糙集定义

粗糙集理论[4]可以有效且合理地对各种随机性较强的不确切信息进行分析，还能进一步分析数据，发掘数据的内在规则。利用粗糙集理论对影响冲击地压的各指标进行约简，去除冗余信息，得到精简的冲击地压样本数据。

U/R为R的所有等价知识所构成的非空集合，[x]R为含有x∈U的R等价关系类，一个知识库的全部内容就被看作一个系统关系库K=（U，R），R为U上的一簇等价关系类。

2.1.2 决策表及归一化处理

冲击地压数据处理的知识系统如公式（1）所示[5]。S=

式中：U为对象集；R为属性集，R=C∪D；C为条件属性；D为决策属性；V为属性值构成的集合，V=Ur∈RVr（Vr表示属性r∈R的值域）；f为信息映射，U×R→V，在U中指定对象x的属性值。

决策表即对重要知识系统的表达，是信息决策中至关重要的存在，可以发挥重要作用。为了去除冗余属性，需要对决策表进行行约简，行约简原则如下：如果有相同的条件属性值，决策属性值大多数相同但存在差异，则去除导致决策属性有差异的少数行，保存决策属性取值相同的行；如果遇到条件属性相同、决策属性值不同的两行，可以删除这两行，该样本对分类没有具体意义；如果在决策表中存在条件属性值即决策属性值规律一致的几行，那么就保留其中一行。

由于各影响冲击地压的指标衡量单位有差异且数量级差别很大；因此须对其进行归一化处理，从而避免小数值信息掩埋于大数值样本中。归一化处理如公式（2）所示。

式中：Xk为指标值；Xmax和Xmin分别为各对象所对应指标的最大值和最小值。

2.1.3 基于属性重要性客观权重确定方法

粗糙集理论在进行数据处理时，无须提供数据之外的先验信息，并能够确定各属性的重要性，在进行数据约简时还能够去除不重要的属性。

第i个条件属性的重要性如公式（3）所示。

式中：|·|为集合的势或基数；C-i为条件属性C中第i个指标。客观权重计算方法如公式（4）所示。

冲击地压综合权重如公式（5）所示。

式中：qi为客观权重；pi为主观权重，由AHP法确定；β为经验因子，反映了决策过程中决策者对主观权重和客观权重的偏好程度，β越小，表明决策者越重视专家的经验知识，反之，表明决策者越重视客观权重。

2.2 层次分析法（AHP法）

层次分析法（AHP法）[6]是对一个复杂的多目标决策问题，按它们之间的相互关系分解成最高层、中间层和最低层，并绘制层次结构模型图，最高层即为目标层，中间层即考虑因素和决策准则，最低层即决策时的备选方案。通过对指标进行模糊量化计算，求得中间层和最低层的各指标对最高层指标的优先权重，最优方案为权重最大者。

构造判断矩阵及其一致性检验的步骤如下。确定AHP法的权重是对各因素间的相互重要性进行两两比较，进而构成判断矩阵的方法。aij为因素i与因素j的重要性比较，具有如公式（6）所示的性质。

判断矩阵中aij的标度方法见表1。

表1 判断矩阵中aij的标度方法

判断矩阵最大特征根λmax的特征向量，经归一化处理后得指标权重。随后对其进行一致性检验[7]。用λmax-n数值的大小来衡量判断矩阵的不一致程度。定义一致性指标CI如公式（7）所示。

式中：n为判断矩阵阶数。

检验系数CR如公式（8）所示。

式中：RI为判断矩阵的平均一致性指标值。

RI的值与判断矩阵的阶数有关，其对应关系见表2。

表2 平均随机一致性指标

如果CR<0.1，那么表明判断矩阵具有满意的一致性，否则就需要对判断矩阵进行调整，直至具有满意的一致性。

3 实验数据采集与结果分析

该文通过煤岩体动力破坏力学实验模拟煤岩体冲击地压的发生过程，实验样本取自鸡西市某矿区，该矿区曾发生顶板与煤层冲击地压的灾害，通过现场取样，将样本作为煤岩体试样。取样的样本是高为100 mm、半径为25 mm的圆柱体；实验设备是由SH-Ⅱ声发射系统以及ROCK600-50三轴实验仪组成，设备如图3所示。实验的固定静水压力为5 MPa，ROCK600-50三轴实验仪加载速度为1.5 MPa/min，SH-Ⅱ声发射系统传感器的频段设为20 kHz~110 kHz，数据每1 μs采集1次，波形信号门槛值为40 dB。

图3 三轴声发射实验设备图

3.1 粗糙集理论对各项指标权重的确定

该文使用实验数据抗压强度（a）、能量（b）、峰值频率（c）以及信号强度（d）对冲击地压进行综合评价。使用粗糙集理论对冲击地压各项指标进行权重计算，每个评价指标均选取100个实验数据作为评价对象。

抗压强度、能量、峰值频率以及信号强度均为指标值越大，冲击地压事件发生的危险等级越高。抗压强度、能量以及峰值频率的对应权重如下：[0，0.25]权重为0.25，(0.25，0.5]权重为0.50，(0.5，0.75]权重为0.75，(0.75，1]权重为1.00。信号强度的对应权重如下：[0，0.1]权重为0.10，(0.1，0.35]权重为0.35，(0.35，0.5]权重为0.5，(0.5，1]权重为1。冲击地压的危险分为4个等级，分别为无危险（Ⅰ）、弱危险（Ⅱ）、中等危险（Ⅲ）以及强危险（Ⅳ），对应的权重区间分别为[0，0.25]、(0.25，0.5]、(0.5，0.75]和(0.75，1]。由此可以建立评价指标的分级情况。

根据公式（2）对原始数据进行归一化处理，并根据所划分的各类区间的冲击地压危险等级确定评价对象的危险等级，见表3。

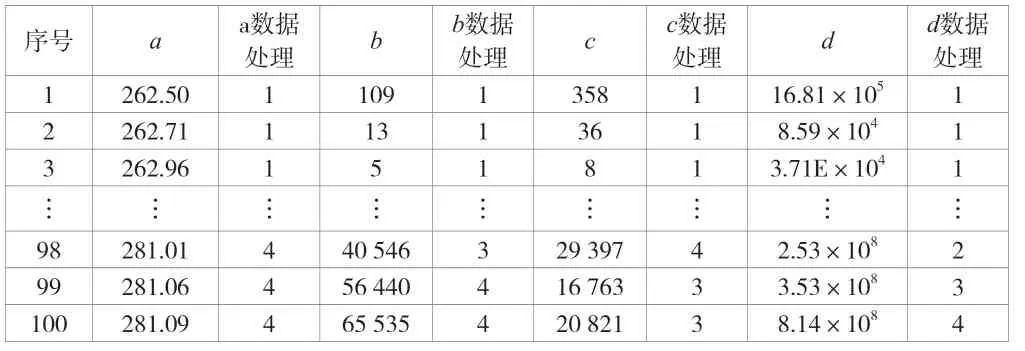
表3 冲击地压评价对象危险等级

3.2 AHP法对各项指标权重的确定

首先建立冲击地压各评价指标的层次结构，层次规则见表4。

表4 AHP法层次规则表

构建判断矩阵A-B，见表5。

表5 判断矩阵A-B

同理可得判断矩阵B1-C，见表6。

表6 判断矩阵B1-C

计算判断矩阵的最大特征根λmax并根据公式（7）和公式（8）进行一致性检验。

判断矩阵A-B：λmax=2.0000，CR=0.0000<0.1，通过矩阵一致性检验。

判断矩阵B1-C：λmax=3.0858，CR=0.0740<0.1，通过矩阵一致性检验。

3.3 综合权重

选取经验因子β=0.7，由公式（5）可得冲击地压各指标综合权重，结果如下。

冲击地压危险综合评价结果见表7。

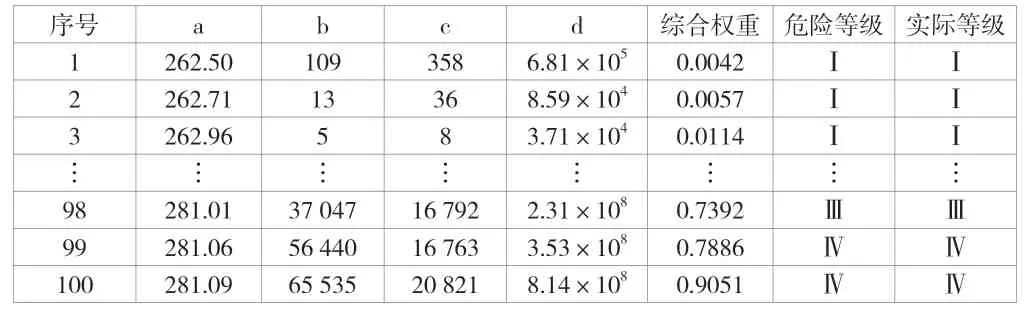
表7 冲击地压危险综合评价

4 结论

粗糙集理论旨在分析冲击地压随机性较强的不确切信息，去除冗余信息，确定各指标的客观权重，并使用AHP法按照冲击地压各指标间的相互关系对其进行分解，确定其主观权重，弥补了粗糙集理论对实验数据的依赖性。利用AHP-粗糙集理论对发生冲击地压时煤岩体的抗压强度、能量、峰值频率以及信号强度的权重进行分析，将主、客观权重相结合，给出冲击地压事件发生的危险性的综合评价结果，并与实际结果进行比较，基本与实际结果符合。因此，采用AHP-粗糙集理论对冲击地压事件发生概率进行综合评价，可以有效地对冲击地压事件发生的概率进行预测，降低冲击地压发生所造成的危害。