BP 神经网络辅助的SINS/GPS 组合导航姿态误差补偿方法研究*

王 超，周 军，黄浩乾，沈寒伊，唐家成

(河海大学能源与电气学院,江苏 南京 211100)

在捷联惯导系统(SINS)中惯性测量元件(陀螺和加速度计)与运载体固联,通过计算机采集惯性元件的输出信息并进行数值积分,求解运载体的姿态、速度和位置等导航参数。高精度SINS 对惯性器件性能和导航算法精度的要求非常苛刻,但由于高精度惯性器件价格昂贵且提升其精度非常困难,所以在影响SINS 的误差源中要求导航算法误差比重必须很小,一般需小于5%[1]。由于载体姿态可能剧烈变化(如战斗机的翻滚运动),姿态更新算法便成了SINS 算法的核心,对解算精度影响最为突出,具有重要的研究和应用价值。

相对单一的惯导解算,SINS/GPS 组合导航利用SINS 解算得到的速度、位置和GPS 输出的速度、位置的差值构建观测量,通过Kalman 滤波器对惯性解算误差进行最优估计,利用估计出来的误差修正惯性解算结果,从而大大提高导航解算精度。但实际上,GPS 信号受建筑遮挡、载体机动等因素影响可能失锁,Kalman 滤波器失去了一部分观测量,会导致导航系统精度下降甚至发散。针对这些问题,有学者提出了利用神经网络辅助的方法[2-6]。其基本思想是利用GPS 信号有效时的导航数据训练神经网络,在GPS 失效时接入该训练好的网络,由其预测出组合导航数据,使导航结果不发散。鲍泳林等[2]以惯性器件测量数据为输入,Kalman 输出的状态估计作为标签对径向基函数神经网络(Radial Basis Function Neural Network,RBFNN)进行训练,并利用训练结果对滤波器进行校正；陈鑫鑫等[3]以不同时刻纯惯性解算的速度和位置差值为输入,以组合导航结果为输出,对多个BPNN 并行进行训练；林雪源[4]、刘庆元[5]采用MEMS 传感器测量数据为输入,Kalman 滤波器输出的水平速度和位置误差作为标签对RBFNN 或前馈神经网络(Back Propagation Neural Network,BPNN)进行了训练；李松等[6]对基于BPNN 神经网络辅助的导航滤波方法进行了探索和论证,提出利用滤波残差和增益进行网络训练的方法。但对这些方法进行SINS/GPS 组合导航数值仿真时,利用滤波残差对神经网络的训练效果不明显。采用滤波增益矩阵虽可取得较好效果,但涉及要素过多,以SINS/GPS 组合导航问题为例,增益矩阵为15×6 维,则要求至少90 个输入层神经元,使得训练速度过慢,算法过度冗余。

结合目前SINS/GPS 组合导航的主要问题[7]和近年来神经网络算法技术[8-9],研究目标为:

(1)在SINS/GPS 组合导航方法上引入BP 神经网络辅助修正环节,以提高组合导航姿态估计精度；

(2)完善并优化神经网络训练环节,构建降维特征向量,减少网络的计算冗余,提高训练效率。

1 SINS/GPS 组合导航模型

SINS/GPS 组合导航系统通常选用捷联惯导的误差传播方程作为其状态方程,选择“东-北-天”地理坐标系为导航系,取姿态失准角(φx,φy,φz)、速度误差量、位置和陀螺常值漂移(εE,εN,εU)、加速度计常值偏置(∇E,∇N,∇U),同时考虑杆臂误差和时间不同步误差(δt),可获得以速度和位置误差为状态观测量的SINS/GPS 组合导航状态空间模型,如下

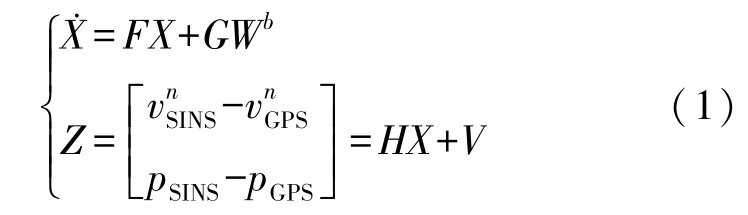
式中:X=[φT(δvn)T(δp)T(εb)T(∇b)T(δlb)Tδt]T,而

更确切地,F为系统状态转移矩阵；G为系统噪声驱动矩阵；Wb为系统噪声矢量,和分别为陀螺角速度测量白噪声和加速度计比力测量白噪声；V为测量噪声矢量,Vv和Vp分别为GPS 接收机速度测量白噪声和位置测量白噪声；H为系统的量测矩阵,其他符号含义参见严恭敏等[1]的4.2.5 节。需要注意的是,为简化符号表示,式(1)中的时间变量t均省略不写,也就是说,SINS/GPS 组合导航状态空间模型(1)是线性时变的。

一般情况下,如果条件允许的话,应当对SINS和GPS 之间的杆臂(或时间不同步)误差进行精确测量并作相应补偿,不再将它们列入滤波器状态,这样既有利减少滤波计算量,还能防止杆臂(或时间不同步)状态估计不准而影响其他状态的估计效果。实际应用中,如果杆臂(或时间不同步)误差难以精确测量,或随时间变化,才考虑其状态建模和滤波估计,并且只有在适当机动的情况下,这些状态才是可观测的。下文不考虑将它们列入滤波器状态,故X为15 维的矢量。

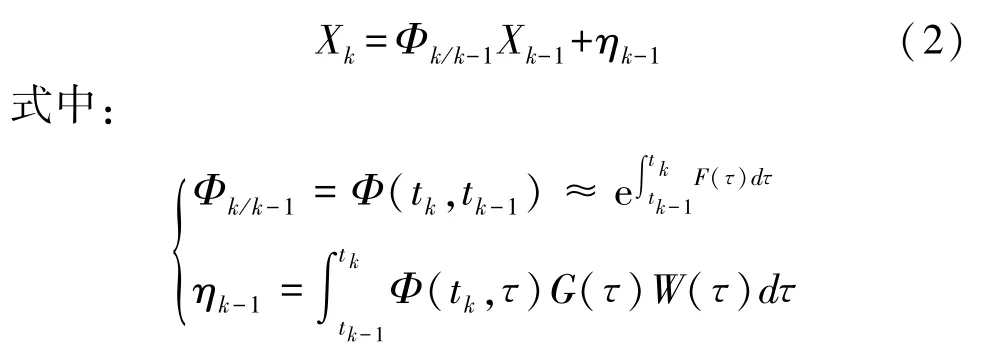
F(τ)、G(τ)是关于时间τ的确定性矩阵,w(τ)是零均值的高斯白噪声,式(2)的详细推导请参见文献[1]。

记离散化时间间隔为T=tk-tk-1,当F(t)在较短的积分区间[tk-1,tk]内变化不太剧烈,并且满足F(tk-1)T≪I时,则Φk/k-1可近似为:

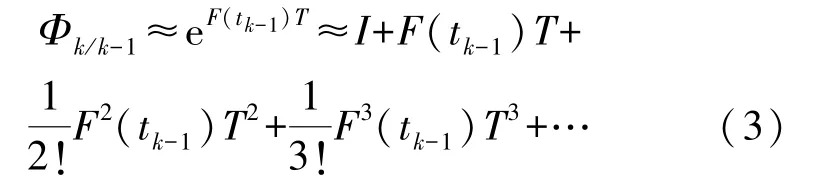
忽略高阶项后得到k时刻系统离散状态方程为:

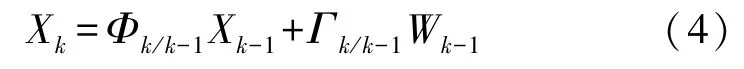
式中:Φk/k-1、Γk/k-1为离散化后的状态转移矩阵和噪声驱动矩阵,它们可以表示为:

式中:F(tk-1)表示上一时刻系统状态转移矩阵,G(tk-1)表示上一时刻系统噪声驱动矩阵。

根据上述离散状态方程和量测方程,通过Kalman 滤波的SINS/GPS 组合导航姿态估计如下:

2 BP 神经网络辅助的SINS/GPS 组合导航系统设计

2.1 BP 神经网络算法

BP 神经网络算法是目前应用广泛的函数逼近方法。按照误差反向传播方法训练后的BP 神经网络是一种多层前馈网络模型,包括输入层,一个或多个隐藏层和输出层。采用包含一个隐藏层的网络模型。研究表明,包含一个隐藏层的神经网络可以逼近任何函数模型[10],如图1 所示。BP 神经网络的传播过程包括正向和误差反向传播两个过程,正向传播指输入信号通过隐藏层作用于输出层,期间经过激励函数的非线性变换,产生输出信号。若实际输出与期望输出不相符,则转入误差反向传播过程。将输出误差通过隐藏层向输入层逐层反传,并将误差分摊给各层所有单元,以从各层获得的误差信号作为调整各层权值的依据[11]。

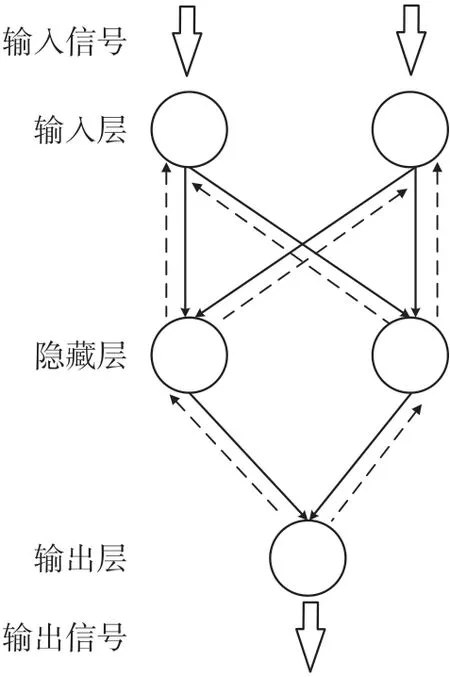
图1 BP 神经网络结构图

通过调整输入层与隐藏层和隐藏层与输出层的连接强度、阈值,使误差沿着梯度方向下降,经过反复迭代,即网络训练过程,直到网络输出和期望输出间误差接近于零或预定阈值,停止训练[12]。

BP 神经网络在组合导航领域的应用时,问题主要集中在特征向量的构建和估计上。

2.2 通过QR 分解构建降维姿态特征向量

通过文献分析,我们可以看到神经网络辅助的组合导航系统主要采用滤波残差、增益来构建特征向量。滤波增益虽可以达到理想的效果,却因组合导航系统状态向量维数较大,训练速度十分缓慢。对此,考虑基于矩阵QR 分解构造神经网络的输入特征向量。QR 方法是一种等价变换方法,是计算一般矩阵特征值问题的有效方法之一。

定义1 如果矩阵A可以化成适当维数的正交矩阵Q与上三角矩阵R的乘积,即

则称式(7)是矩阵A的QR 分解。

需要注意的是,A矩阵可以是非方矩阵,而Q矩阵是与A的行数相同的方矩阵,R具有与A相同的行列数,即R也可以是非方矩阵。

基于定义1,关于矩阵A的QR 分解的主要性质与算法特征可归纳为如下的引理[13]。这些引理的结论对于理解本文的姿态估计算法的状态特征向量的降维处理的有效性和可行性有关键作用。

引理1假设m≥n,设A为m×n矩阵,且n个列向量线性无关,若A是列满秩矩阵,即rank(A)=n,则存在矩阵分解式

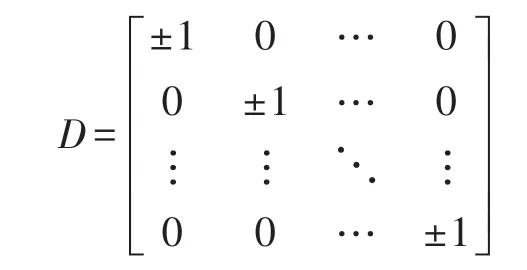
式中:Q为m×m正交矩阵,R为m×n上三角矩阵,且除去相差一个对角元素的模全为1 的对角矩阵因子D外,分解式(8)是唯一的。其中

备注1引理1 的结论说明矩阵A的QR 分解若存在的话具有唯一性,该唯一性正好对应了增益矩阵特征(具有代表性)的唯一性。基于这样的理解,将(6)式定义的Kalman 滤波算法的增益矩阵Kk进行QR 分解就可以有效地将增益矩阵的主要特征要素提取出来,形成低维的参数向量,使得特征信息的提取可以在低维向量空间中完成,从而大大简化运算关系,降低运算量。这对于提高相应的载体姿态估计算法的效率无疑是有用的。

更具体地,对式(6)中的滤波增益矩阵Kk进行QR 分解,将Kk分解成Q15×15和R15×62 个矩阵的乘积,具体形式如式(9)所示:

这里,Q15×15和R15×6的定义方式是显然的。

提取R15×6阵的上三角子矩阵中的所有非零元素行向量进行列堆叠用于构建神经网络的输入特征向量Xin=[r1,1,r1,2,r1,3,…,r6,6]T,由式(9)可知,该特征向量仅有21 个元素,而非原来的90 个。因此,利用QR 分解提取增益矩阵的主要特征,可以显著减小神经网络输入特征向量的维数,在不影响算法性能的前提下,有效提高BP 神经网络的训练速度和组合导航算法的计算效率。

备注2由式(6)的第二式可知

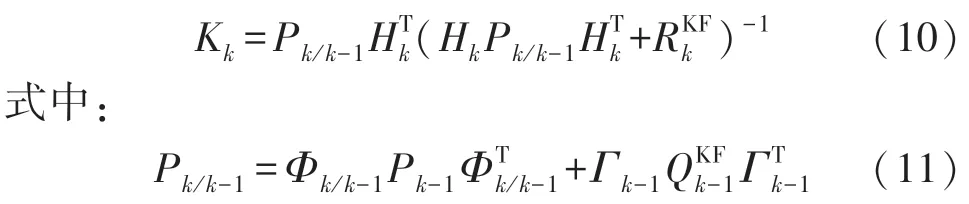
为此,接下来证明Pk/k-1是可逆的。上文已经说明必正定,所以至少是半正定的；而Pk-1是我们通过先验给出初始值P1后逐次迭代产生的,所以,只要Pk-1是正定的(P1总可以给定为正定的),结合状态转移矩阵Φk/k-1的非奇异性,可以得出一定是正定的。最后,根据如下引理可知,Pk/k-1必为可逆矩阵。

引理2如果A和B是正定矩阵,则对任何不同时为零的向量x和y,则有xTAx＋yTBy＞0。

以上备注2 的讨论表明,在一定条件下Kalman滤波的增益矩阵的QR 分解处理总是存在的。

2.3 Kalman 滤波器设计

采用基于QR 分解Kalman 滤波的增益矩阵构建神经网络特征向量的方法,可有效地减小输入特征向量的维数,进而提高网络训练速度。BP 神经网络结构图如图2 所示。

图2 QR 分解后的BP 神经网络结构

BP 网络输出量的物理含义为姿态估计误差,即:

在完成网络训练后,即可利用BP 神经网络的输出信息来辅助修正组合导航的滤波估计结果,整个系统构成如图3 和图4 所示。

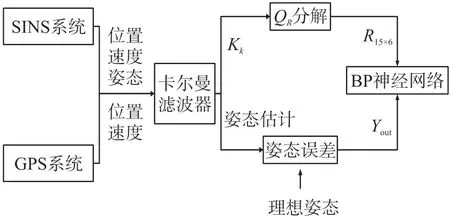
图3 基于神经网络的Kalman 滤波算法训练流程图

图4 使用BP 神经网络修正滤波结果的流程图

备注3SINS 可以输出载体系统的位置、速率、姿态,GPS 可以输出系统的位置、速率,但无法得到姿态。Kalman 滤波器的观测方程是依靠SINS 和GPS 的位置、速率差构建的(见式(1)的Z),SINS 和GPS 信息就是由此来混合的。SINS 的姿态输出信息则体现在式(1)的F阵里面,这些信息要一并输入才能计算Kalman 滤波方程。滤波结果是SINS 导航的解算误差,利用这些误差就可以实现补偿SINS解算的设计要求。

在常规Kalman 滤波算法的基础上,加入BP 神经网络辅助修正环节具体就是,首先对滤波增益矩阵Kk进行QR 分解,然后提取R阵中非零元素构建BP 网络的输入特征向量。最后利用网络的输出结果辅助修正滤波估计值,即可以进一步提高组合导航系统的姿态估计精度。

3 仿真验证

为验证BP 神经网络辅助的SINS/GPS 组合导航算法的有效性,通过2 组仿真实验进行验算。对比不同工况下QR 分解构建特征向量的BP 神经网络辅助的Kalman 滤波算法(Back Propagation based on QR Kalman Filtering,BP-QRKF)与常规Kalman滤波算法(Kalman Filtering,KF)的估计精度。

具体地,输入特征向量为21 维,对应(9)式中R阵的21 个非零元素。设置隐含层神经元个数为24个,采用Sigmoid 激活函数；输出层神经元个数为3个,采用Purelin 函数线性输出。

3.1 仿真实验1

实验1 主要验证QR 分解的神经网络特征向量构建方法的可行性。验证QR 分解法能否在不影响导航精度的情况下有效缩减输入特征向量的维度,提高算法的效率。仿真时间设置2 500 s,载体运动状态为静止,SINS 和GPS 精度如表1 所示。

表1 仿真器件参数

首先直接利用滤波增益矩阵Kk(不采用QR 分解法)构建特征向量,此时网络输入为90 维,仿真结果如图5 所示。

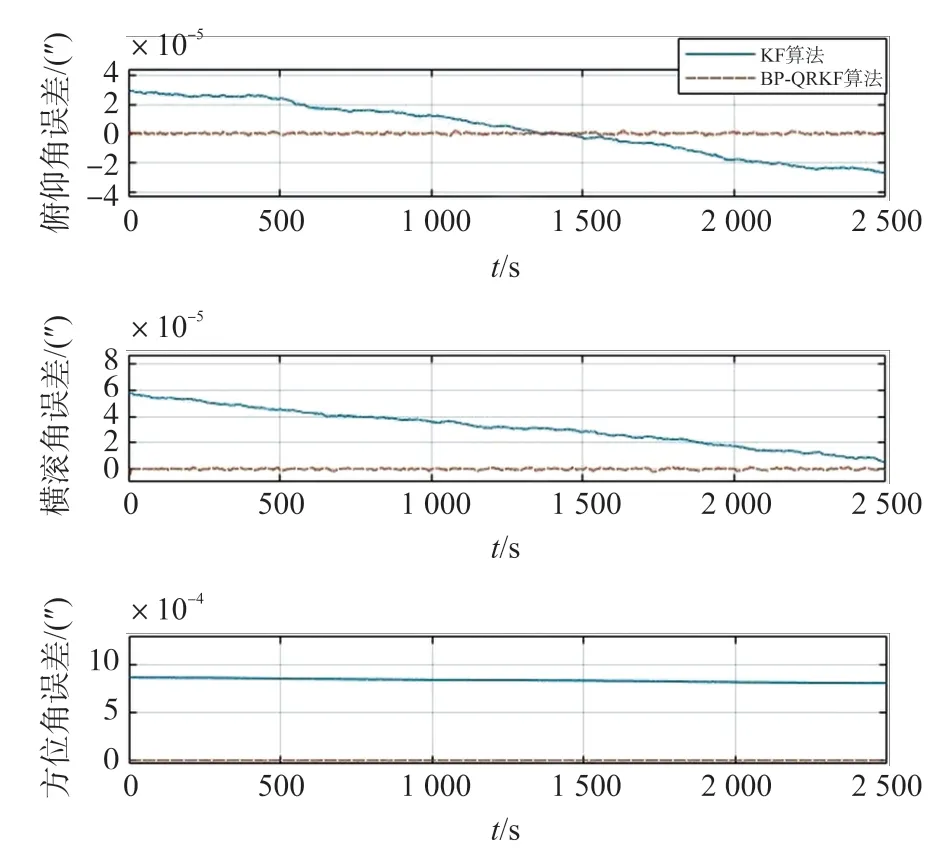
图5 BP-QRKF 算法(未采用QR 分解)与常规KF 算法滤波精度对比

为了直观起见,将方位角误差曲线进行放大,结果如图6 所示。

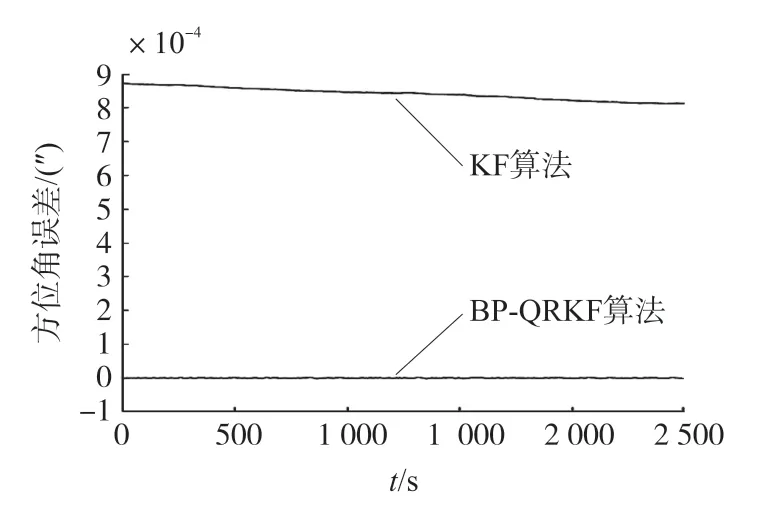
图6 方位角误差放大图

虽然此时BP-QRKF 算法精度优于常规KF 算法,但由于未对Kk精简,导致BP 网络的输入特征向量维度过高,计算耗时过大。BP 神经网络单次训练平均耗时及组合导航滤波估计精度如表2 所示。

表2 未采用QR 分解法仿真结果统计

若利用QR 分解Kk,提取R阵中非零元素作为输入特征向量,仿真结果如图7 所示。

图7 BP-QRKF 算法(采用QR 分解)与常规KF 算法滤波精度对比

BP 神经网络单次训练平均耗时及组合导航滤波估计精度如表3 所示。

表3 采用QR 分解法仿真结果统计

对比图5 与图7 和表2 与表3 可得出以下结论:

(1)无论是否采用QR 分解,采用神经网络补偿后的KF 算法的姿态估计精度均优于常规KF 算法。

(2)采用QR 分解后,将BP 网络输入向量由90维减少到21 维,网络规模显著减小,单次训练时间从20 s 缩短到0.67 s,提高了2 个量级。

(3)采用QR 分解对Kk进行特征变量的精简,滤波估计精度并没有下降,这说明QR 分解法可有效保留滤波增益矩阵的特征。

3.2 仿真实验2

用3.1 训练完成的神经网络进行实际静态姿态估计,时长设置为150 s,用于测试算法的鲁棒性。

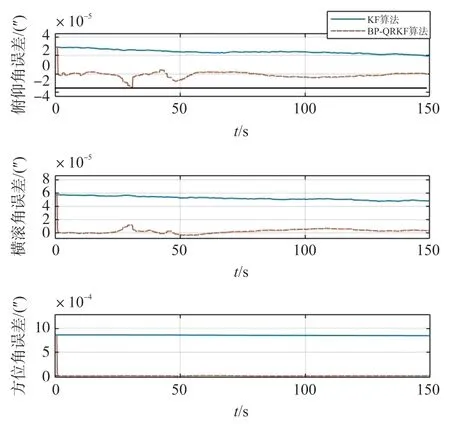
图8 BP-QRKF 算法与常规KF 算法滤波精度对比

为了直观起见,对方位角误差图进行放大,结果如图9 所示。

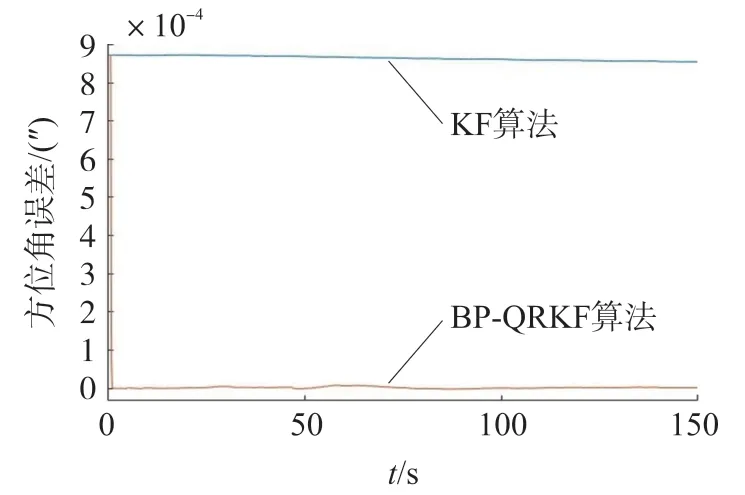
图9 方位角误差放大图

实际静态组合导航滤波估计精度如表4 所示。

表4 仿真结果统计

可以看出,静态姿态估计精度提高了2 个数量级(3.1 节中的算例实际为4 个数量级)。这是由于GPS 信号是每隔一段时间才会发送,算法一开始接收不到量测信息,导致无法计算滤波增益矩阵Kk,所以BP-QRKF 算法一开始无法对姿态估计进行补偿。当有了GPS 信号后,提案方法就可以很好地补偿KF 的姿态估计结果。

4 结论

BP 神经网络辅助的SINS/GPS 组合导航方法,利用QR 分解法构建神经网络特征向量,辅助修正Kalman 滤波的姿态估计结果。经过仿真验证,相较于传统方法,神经网络辅助的组合导航系统可以达到更高精度,对未来组合导航技术发展具有明确的参考价值。

需要指出的是,滤波增益矩阵Kk的更新依赖于GPS 的信息,如今GPS 可以以较高频率输出信息,然而算法由于没有考虑动态参数,故而对动态实时姿态估计的补偿效果较差。今后的研究工作可以考虑把更新频率较快的惯性测量元件(陀螺和加速度计)的输出信息加入输入特征向量,探讨动态姿态估计的高速补偿算法的开发问题。