基于滑模控制的汽车电子助力转向系统性能研究*

何伟丽，赵 伟

(1.驻马店职业技术学院机电工程系,河南 驻马店 463000；2.河南科技大学车辆与交通工程学院,河南 洛阳 471003)

汽车已普遍应用于人们的生产生活,电子助力转向系统(Electric Power Steering,EPS)是汽车中的关键部件之一,直接决定了汽车的转向性能和驾驶人员的操纵性和舒适性。在汽车驾驶过程中,不同路况环境对转向性能要求有所差异,因此要求EPS控制器具有一定的抗干扰能力和鲁棒性,以满足不同工况条件对汽车EPS 系统的性能需求,为此国内外诸多学者针对EPS 系统性能提升展开了广泛深入的研究[1-3]。

EPS 中控制算法是保证系统性能的核心内容,先进的控制算法可以根据车辆速度、转向盘转角和力矩等信号确定理想助力信号,且通过助力电机补偿实现。Ciarla V 等[4]研究相同车速条件下助力力矩与转向盘指令力矩的数学关系,进而根据Stevens能量法则和位置目标控制方法进行系统辨识和补偿。Lee D 等[5]确定了车速与转向盘转角变化对应的理想转向盘力矩关系,并根据转向盘理想转矩与反馈的实时力矩的偏差实现闭环反馈控制,但此方法易引起系统出现不稳定震荡,普适性较差。向铁明等[6]用二次多项式拟合车速与补偿力矩,通过曲线型助力特性实时补偿,使系统实现连续均匀的助力效果,但控制系统计算量大,响应速度慢。为此余为清[7]将助力特性曲线离散化,通过预分段模式进行助力特性补偿,减小了电子控制单元的计算量,提高了系统动态响应能力。上述文献主要针对已知或辨识确定的理想助力特性曲线,实现对助力特性的补偿,实际使用过程中受限于EPS 系统助力特性差异的影响,难以广泛使用。

针对上述问题,张博[8]、张虎[9]等利用观测器确定助力电机的转速,再根据车速、转向盘角速度等信息确定助力电机实时补偿量,在控制器基础上在线补偿,有效改善了EPS 系统助力性能。Yamamoto 等[10]提出一种基于扩展LPV(linear parameter varying)的状态反馈控制方法,利用控制器运算得到助力电机在线补偿量,实现EPS 系统对传动环节中的扰动特性的在线补偿。上述算法需确定干扰类型及其基本形式,再利用控制器或观测器对其补偿。为有效提升EPS 系统性能,本文提出一种基于滑模控制器的在线补偿策略,根据车速、转向盘转角及其角速度、角加速度等信息,在线实时确定助力电机补偿量,在保证系统稳定的基础上,利用控制器实现EPS 转向助力特性和摩擦特性的补偿。

1 EPS 动力学模型

图1 为典型的EPS 结构示意图,电子控制单元(Electric Control Unit,ECU)可以根据转向盘转角、车速及转向盘角速度等信号实时处理计算,确定助力电机的助力电流,通过电机驱动执行机构实现电动转向助力的功能[11]。

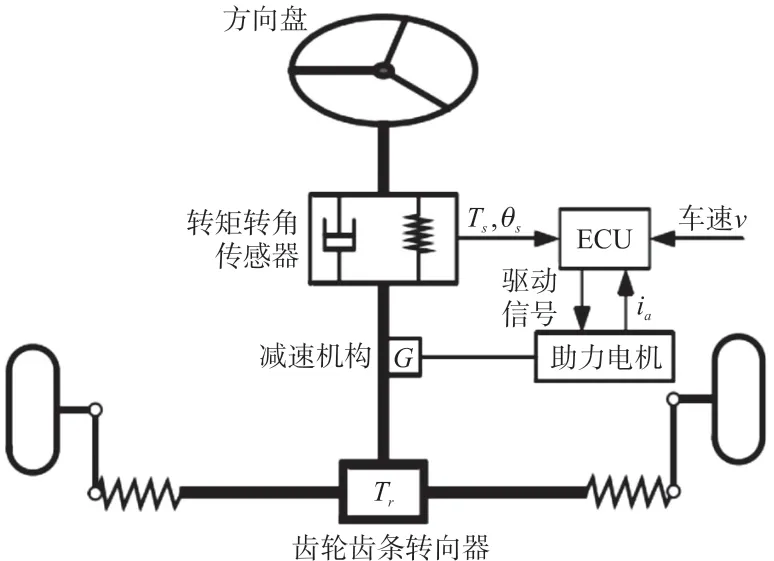
图1 EPS 结构示意图

首先对图1 的EPS 结构示意图进行受力分析,有

式中:Jh为执行机构转轴处的等效转动惯量,θh为执行机构转轴处的转动角度,为角速度,为角加速度,Td为通过助力电机输入至转轴的转矩,Ks为转轴的抗扭刚度,Rs为驱动轮的齿轮半径,bh为转轴的抗扭阻尼系数,xr和Tfh分别为齿轮齿条传动机构对应的位移和运动瞬间的非线性转动摩擦扭矩。

为了将EPS 电机旋转输出变换为直线输出,对系统中的齿轮齿条传动机构建模得到式(2)

式中:m为差速器结构中横向拉杆的质量,x为横向拉杆的位移,br为运动副中的阻力系数,Ftr为驱动横向拉杆的驱动力,Km助力电机输出扭矩刚度,G为传动比,xr为直线运动的横向位移。其中,Rs为驱动轮的齿轮半径,θm为负载处的转动角度。

2 滑模控制器设计

图2 为基于滑模控制器的EPS 控制结构图,系统中的机械传动环节不可避免存在摩擦力,如粘滞摩擦和静摩擦力等,且系统中常含有未知扰动,传统的控制器结构在应对上述扰动时,稳态精度和动态响应能力存在不足。传统的基于观测器和前馈补偿的控制方法通常需要辨识干扰的数学模型,为此本文将设计滑模控制器,抑制系统未知干扰,提升系统的动态响应精度和速度。

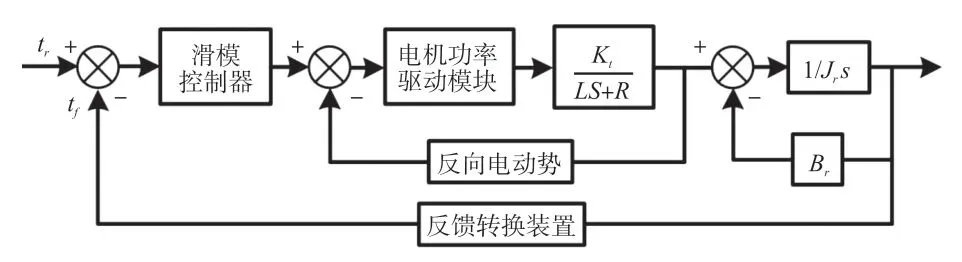
图2 基于滑模控制器的EPS 控制结构图

根据图2 的基于滑模控制器的EPS 控制结构图可知,系统的输入为力矩指令,经过控制器运算处理后输出电压/电流信号驱动电机功率模块,进而实现电机带动执行机构动作。为设计合理的滑模控制器,针对图2 的控制结构图,定义基于转矩输入的误差表达式(3)

式中:tr为EPS 系统输入指令转矩,tf为EPS 被控对象输出转矩,et为指令转矩与系统反馈转矩的偏差。根据滑模控制理论定义EPS 滑模切换面为(4)

根据式(4)可以求得滑模切换面的微分表达式为

根据助力电机电压方程式可以得到式(6)

式中:Kt为助力电机的转矩系数,L和R分别为助力电机线圈的感性负载和阻性负载,ut为根据et和滑模控制器运算处理输出的指令电压,it为ut经过电机负载线圈的励磁电流,ω为助力电机的转动角速度,ψm为助力电机的磁链。

为抑制EPS 的未知干扰,提高系统鲁棒性和动态响应能力,设计式(5)中的滑模切换面微分表达式如式(7),sgn(s)中的s为拉普拉斯算子。

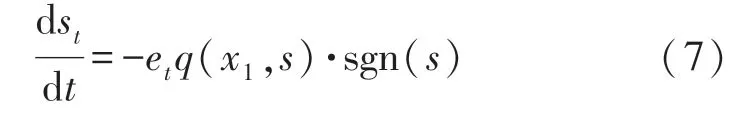
式中:

式中:x1、k、δ和ε为典型滑模切换面微分表达式中的常数变量,需要根据实际系统确定。

联立式(5)～式(7)可以得到

对式(9)进行变换后可得滑模控制器输出的控制量

为保证所涉及滑模控制器的稳定性,本文选取李雅普诺夫稳定性判据来判断所涉及控制器的稳定性,选取李雅普诺夫函数为

当式(12)成立时,即李雅普诺夫函数的导数小于零,即可以证明所涉及的滑模控制器满足稳定性要求。

将所提出的滑模控制器表达式代入式(12)可以得到

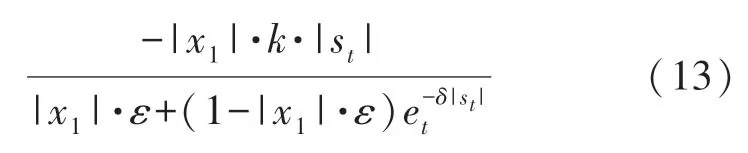
当式(13)满足k＞0、δ＞0 和0＜ε＜1 的条件时,式(13)中的分母恒非负,即得到

根据李雅普诺夫稳定性判据可以证明本文所提出的滑模控制器满足稳定性要求,在有限时间内利用本文所提出的滑模控制器能够使EPS 系统达到预期的滑模切换面,进而实现渐进稳定。

3 EPS 系统架构

本文所述EPS 机电控制系统架构如图3 所示,主要包括方向盘、扭矩传感器、转角传感器、加速机构、控制器和电机驱动器等,相关硬件装配于试验样机中。其中EPS 控制器采用Microchip 公司生产的dsPIC30F6012 作为系统运算处理微控制器,此控制器具有丰富外设资源且兼具数字信号处理器所具有的数据运算和传输能力。

图3 EPS 机电控制系统架构

针对图3 的试验样机,主要利用dsPIC30F6012为控制器实时采集转矩信号、转角信号、车速信号和助力电机反馈的实时电流,并根据上述信号采用相关控制算法运算处理输出控制量即目标电流,再经过电机驱动器的功率放大作用驱动助力电机带动执行机构实现电子转向助力的目标。

为了探究本文所提算法对EPS 控制性能的影响,将助力电机驱动器设定为电流环模式,根据相关传感器反馈信号,利用dsPIC30F6012 微控制器实现基于滑模控制算法的闭环反馈控制,即通过微控制器输出指令转矩(目标电流)至电机驱动器。表1为EPS 机电控制系统中所使用的传感器和执行机构的特性参数,主要包括传感器测量量程和对应的模拟量电压值,机械传动执行机构的减速比及助力电机基本参数,如电感、电阻和转矩系数等,此类参数为在微处理器中实现滑模控制算法提供依据。

表1 传感器和执行机构特性参数

4 试验验证

针对前文所述的EPS 机电控制系统架构,在Microchip 公司生产的dsPIC30F6012 微处理器中实现所提出的滑模控制器,通过给定指令转矩和转矩传感器反馈的实际转矩对比分析,反映不同控制算法动态特性。为了对本文所提算法进行对比分析,实验所使用的控制器模型为传统PID 控制器、传统滑模控制器和本文所提出的滑模控制器。图4 为EPS 系统不同控制算法下的阶跃响应,3 种控制器均能实现稳定状态,且无稳态误差,传统的PID 控制器较其他两种方法超调较大,调整时间较长。传统的滑模控制器能够实现良好的动态响应,但其超调性能低于本文所提滑模控制算法,且传统滑模算法的动态跟踪误差振幅较大,存在一定的抖振,易使系统在干扰状态下不稳定。

图4 不同控制算法的EPS 系统阶跃响应

为了充分验证算法动态跟踪能力,在微控制器中执行图5(a)所示的正弦指令转矩输入,其频率为1 Hz,振幅为10 N·m,动态响应如图5(b)和5(c)所示。基于传统的PID 控制器,EPS 系统在跟踪图5所示的指令转矩时,其转矩跟踪误差的均方根值为0.46 N·m；基于传统的滑模控制算法,其动态转矩跟踪误差的均方根值为0.24 N·m；利用所提出的滑模控制算法,其转矩跟踪误差的均方根值为0.13 N·m。综上所述,基于所提出滑模控制算法的控制器能够在一定程度上抑制系统内部粘滞摩擦、静摩擦及非线性扰动,此方法具有良好的普适性,具有稳态精度高,动态响应快速准确,稳定性好的优点,为广泛应用于EPS控制系统奠定基础。

图5 正弦指令输入下的EPS 系统动态响应

5 结论

本文针对传统EPS 动力学模型,分析影响系统稳态精度和动态响应特性的因素,提出了一种新型滑模控制算法。此方法能够有效抑制系统扰动,克服系统内部摩擦力对动态性能的影响,与此同时,此控制方法具有稳定性好的优点。利用李雅普诺夫判据从理论上证明了所提算法的稳定性。通过实验,在EPS 样机中验证了算法对阶跃指令和正弦转矩指令的跟踪能力,对比分析发现,所提算法动态响应特性较PID 控制器和传统的滑模控制算法具有较明显的提升,为算法投入实际应用奠定基础。